响应曲面法优化同向旋转双螺杆挤出机最大固体输送量的研究
袁捷朝,罗 兵,毕 超,王文飞,伊大龙
响应曲面法优化同向旋转双螺杆挤出机最大固体输送量的研究
袁捷朝,罗 兵*,毕 超,王文飞,伊大龙
(北京化工大学机电工程学院,北京100029)
采用响应曲面法对φ34 mm同向旋转双螺杆挤出机的最大固体输送量进行研究。建立了以最大固体输送量为目标函数的二次式多项数学模型,探讨了目标函数的主要影响因素及其交互作用。结果表明,模型所预测的最大固体输送量和实验值之间的误差小于10%,当螺杆转速为124 r/min、螺纹元件螺旋升角为32°、物料粒径为2.7 mm时,最大固体输送量达到534 g/min,这比优化前的最大固体输送量提高了7.2%。
同向旋转双螺杆挤出机;固体输送;响应曲面法;优化
Abstract:The maximum output of solid convey forφ34 mm co-rotating twin screw extruder was optimized by response surface methodology method.A quadratic multinomial equation model using the maximum output of solid convey as the objective function was built,and the main influencing factors and their corresponding relationships were discussed.It showed that the deviation between predicted values by the model and experimental values was less than 10%.The maximum output of solid convey was obtained as follows,screw speed was 124 r/min,the helix angle of the screw was 32°,and the diameter of the solid particle was 2.7 mm.After optimizing the factors,the maximum output of solid convey was 534 g/min and was increased by 7.2%compared with the value before optimizing.
Key words:co-rotating twin screw extruder;solid convey;response surface methodology;optimization
0 前言
双螺杆挤出机在聚合物加工中的应用十分广泛。同向双螺杆挤出机固体输送段主要使用计量加料,螺槽一般为非充满状态,其输送机理较为复杂。近年来国内外的学者也对同向双螺杆的固体输送现象和机理进行了一定的研究。Carrort等[1]认为啮合同向旋转双螺杆固体输送有2种机理,即沿螺槽方向的输送以及在上啮合区沿轴向的正位移输送,并认为上啮合区的正位移输送量就是全部的正位移输送量。Potente等[2]将输送区分成部分填充进料和完全填充压缩区,建立了力和力矩方程,求解得到最大输送量。刘廷华等[3]根据可视化实验观察有色示踪粒子的运动,建立了侧螺槽非充满散粒体态的固体输送模型,以区域型和边界型相结合的数值计算方法求解了应力场和速度场。张沛和郭强等[4-5]利用可视化实验研究螺纹元件中的粉料和粒料输送特性,并建立具有3个子输送区的固体输送理论模型。
虽然前人对固体输送机理和模型进行了大量而有效的研究,但由于固体输送机理较为复杂,影响固体输送行为的因子较多,目前建立的模型与实际情况都有一定的差异,有的模型只考虑了单个因子对固体输送行为的作用,但未考虑因子之间的交互影响。因此,本文拟用响应曲面法来分析同向旋转双螺杆固体输送段最大固体输送量的影响因子,研究其对目标函数的线性、曲面和交互作用,并在研究基础之上对影响因子进行优化。
响应面分析法由1组数学和统计学方法组成,可用于确定各因子及其交互作用在加工过程中对非独立变量的影响,精确地表述因子和响应值之间的关系[6]。采用该统计学方法,能以较少的实验次数和时间对实验进行全面的研究。本文所采用响应曲面法中的Box Behnken设计法是以回归方法作为函数估计的工具,将影响因子和实验结果之间的关系函数化,定量地分析各因子及彼此之间交互作用对响应值的影响。
1 实验部分
1.1 主要原料
聚丙烯,粒料,平均粒径3.8 mm,北京燕山石化公司;
聚对苯二甲酸乙二醇酯,粒料,平均粒径3.1 mm,美国杜邦公司;
聚酰胺6,粒料,平均粒径2.4 mm,北京燕山石化公司。
1.2主要设备及仪器
双螺杆挤出机,LSM30/34,德国Lestritz公司;
台式干燥箱,DG/200-002,重庆试验设备厂。
1.3 实验步骤
主机转速为90~130 r/min-1,螺纹元件螺旋升角为17°~35°,物料粒径为2.4~3.8 mm。由于实验和物料条件所限,实验中选取了3种粒径不同的物料,可能对实验结果产生一定影响。
实验装置如图1所示,实验前先将物料干燥,对每种物料加料量进行标定。挤出机AB段即为挤出机的固体输送段,其长度为10D(D为螺杆外径),可以置换不同螺旋升角的螺纹元件。实验过程中,按照设定值调节螺杆转速,进行计量加料,逐渐增大加料量,得到溢流前的加料量即为该种工况下的最大固体输送量,变换不同升角的螺纹元件、主机转速和物料粒径,得到不同工况下的最大固体输送量并记录,该实验均在常温下进行,机筒不加热。

图1 实验装置示意图Fig.1 Schematic diagram for the experimental equipment
2 结果与讨论
2.1 因素及水平的选取
响应曲面的实验设计分为2个步骤,第一步为单因子实验,其目的为筛选对实验响应值影响较大的因子,单因子实验结果表明,主机螺杆转速、螺纹元件螺旋升角和物料粒径对最大固体输送量有较大影响;第二步为响应曲面实验,其目的为进一步研究影响因子的显著性和交互作用,本文的响应曲面实验采用Design-Expert软件中的Box-Behnken方法,选取主机螺杆转速、螺纹元件螺旋升角和物料粒径作为基础优化因子,以最大固体输送量为响应值,实验因数及水平见表1。

表1 Box-Behnken实验影响因素及水平Tab.1 The factors and their levels of Box-Behnken experiment
2.2响应曲面结果分析
响应曲面实验方案及实测结果如表2所示。方差分析如表3所示。通过对表2的实验数据进行多项式回归分析建立二次响应回归模型,拟合得到二次方程:

从表3可以看出,实验所选用的模型拟合度较好。回归方程的方差分析结果表明,回归方程的F值达到179.02,说明该模型显著,回归方程的决定系数达到99%以上,该模型能够用于双螺杆挤出机最大固体输送量的预测。
式(1)的回归系数显著性检验表明:因子A、B、C对最大固体输送量的线性效应皆显著,因子A2、B2、C2对最大固体输送量的曲面效应显著,因子A C对最大固体输送量的交互效应显著,因子AB、B C对最大固体输送量的交互效应不显著。显著性检验结果见表4。

表2 Box-Behnken实验设计及实测结果Tab.2 Design and result of Box-Behnken experiment

表3 最大固体输送量二次多项式模型方差分析Tab.3 Variance analysis for quadratic polynomial model of the maximum output of solid convey

表4 最大固体输送量回归方程显著性检验Tab.4 Significance test of regressive coefficient from the regression equation of maximum output of solid convey
图2为物料粒径一定(3.1 mm)时,螺杆转速和螺旋升角对最大固体输送量交互影响效应,从图2可以看出,二者的交互作用不显著。
图3为螺旋升角一定(26°)时,螺杆转速和物料粒径对最大固体输送量的交互影响效应,从图3可以看出,当螺杆转速较低时,粒径为3.1 mm时固体输送量达到最大值;当螺杆转速较高时,粒径为2.75 mm时固体输送量达到最大值,这说明螺杆转速和物料粒径对最大固体输送量有着较为明显的交互作用。
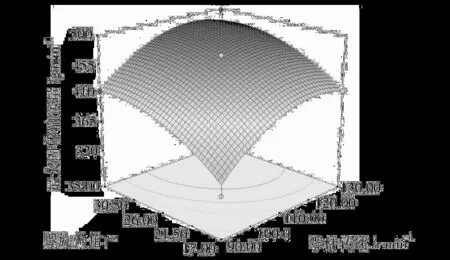
图2 螺杆转速和螺旋升角交互影响最大固体输送量的曲面图Fig.2 Surface layer of the mutual-affection of screw speed and helix angle of screw on the maximum output of solid convey

图3 螺杆转速和物料粒径交互影响最大固体输送量的曲面图Fig.3 Surface layer of the mutual-affection of screw speed and diameter of solid particle on the maximum output of solid convey
图4 为螺杆转速一定(110 r/min)时,螺旋升角和物料粒径对最大固体输送量的交互影响效应。从图4可以看出,二者的交互作用不显著。
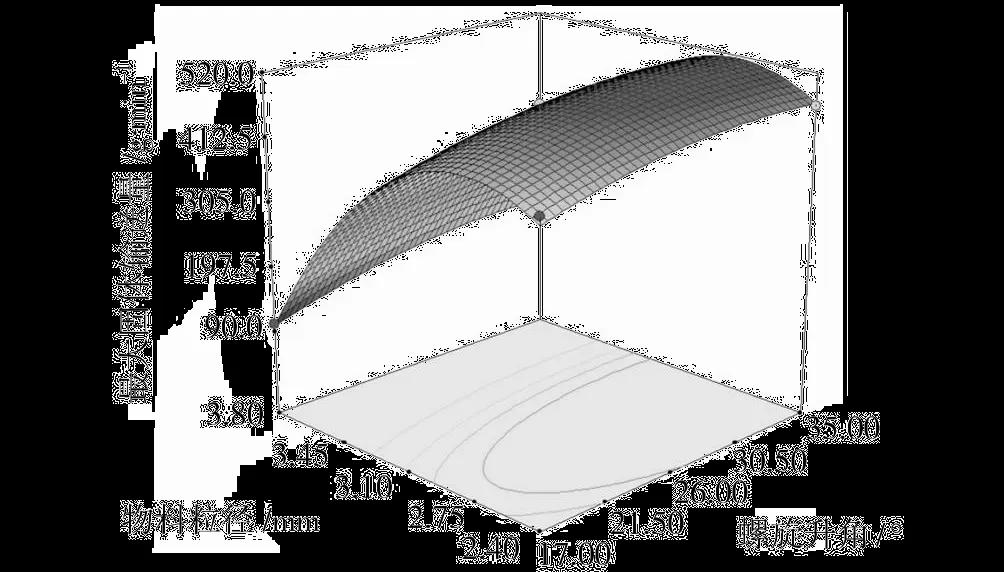
图4 螺旋升角和物料粒径交互影响最大固体输送量的曲面图Fig.4 Surface layer of the mutual-affection of helix angle and diameter of solid particle on the maximum output of solid convey
2.3方程的验证和应用
为验证回归方程(1)的准确性,选取6组前文实验设计中没有用到的工艺条件进行固体输送实验,同时使用回归方程对该6组工艺条件下的最大固体输送量进行预测,将得到的实验结果和回归方程的预测值进行分析和对比,得到的最大固体输送量的预测值与实测值如表5所示。从表5可以看出,理论值和实测值的误差均在10%之内,说明响应曲面法所建立的模型与实验所得到的数据比较吻合,其误差可能来自于实验条件和测量精度的限制。

表5 最大固体输送量的实测值及预测值Tab.5 Experimental values and prediction values of the maximum output of solid convey
对方程(1)的各参数进行优化分析,可以得到3个因子的最佳水平为螺杆转速124 r/min、螺纹元件螺旋升角32°、物料粒径2.7 mm,此时最大固体输送量为534 g/min,这一优化值比表2中固体输送量的最大值提高了7.2%。
3 结论
(1)通过响应曲面法建立了影响主机最大固体输送量的二次多项数学模型,探讨了各因子之间的交互作用。通过对最大固体输送量二次多项式数学模型进行求解,将模型得到的理论值与实测值进行对比,证明该模型与实测值之间的误差在10%以内,能够用于最大固体输送量的预测;
(2)由响应曲面实验分析可知,提高最大固体输送量的最佳水平为螺杆转速124 r/min、螺纹元件螺旋升角32°、物料粒径2.7 mm,此时的最大固体输送量为534 g/min,这一优化值比优化前最大固体输送量提高了7.2%。
[1] Carrot C,Guillet J,MayJ F.Modeling of the Conveying of Solid Polymer in the Feeding Zone of Intermeshing Corotating Twin Screw Extruders[J].Polymer Engineering&Science,1993,33(11):700-708.
[2] Potente H,Melisch U.Theoretical and Experimental Investigations of the Melting of the Pellets in Co-rotating Twin Screw Extruders[J].Int Polym Process,1996,11(2):101-108.
[3] 刘廷华,朱复华.啮合型同向旋转双螺杆挤塑螺槽非充满的固体输送的理论研究(Ⅰ)理论模型[J].中国塑料,1996,10(9):81-85.
[4] 张 沛,耿孝正,朱林杰.同向啮合双螺杆固体输送特性的可视化研究——螺纹元件的粉料输送[J].中国塑料,1999,13(5):90-95.
[5] 郭 强,耿孝正,张 沛.同向啮合双螺杆固体输送可视化研究——螺纹元件的粒料输送[J].中国塑料,1998,12(5):85-93.
[6] Annadurai G,Sheeja R Y.Use of Box Behnken Design of Experiments for the Adsorption of Verofix Red Using Bionpoly[J].Bioproc Eng,1998,18:463-466.
Optimization of Maximum Output of Solid Convey for Co-rotating Twin Screw Extruders by Response Surface Methodology
YUAN Jiechao,LUO Bing*,BI Chao,WAN G Wenfei,YI Dalong
(School of Mechanical Engineering,Beijing University of Chemical Technology,Beijing 100029,China)
TQ320.66+3
B
1001-9278(2011)01-0102-04
2010-08-16
中央高校基本科研业务费项目(ZZ0913)
*联系人,luobing@mail.buct.edu.cn

