基于负荷功率的三相不平衡度的计算方法①

同向前， 王海燕， 尹 军

(西安理工大学自动化与信息工程学院， 西安 710048)

基于负荷功率的三相不平衡度的计算方法①

同向前， 王海燕， 尹 军

(西安理工大学自动化与信息工程学院， 西安 710048)

三相不平衡度的估算是贯彻国家标准、提高电能质量的基础，故提出一种三相三线配电系统中由不对称负荷引起的三相不平衡度的实用计算方法。在引入了三相不对称负荷的序容量的概念之后，负荷电流不平衡度等于负荷负序容量与正序容量之比，由该不对称负荷在某公共连接点引起的三相电压不平衡度等于负荷负序容量与系统短路容量之比；建立了三相不对称负荷的序容量与负荷相间功率之间的函数关系，简化了三相不平衡度的计算过程。算例表明该方法简便易用。该方法适合于工业配电网在设计规划阶段对三相不平衡度的估算。

三相负荷序容量； 三相不平衡度； 不对称负荷； 电能质量

电力系统三相不平衡主要是由于三相负荷不对称所致[1]，典型的不对称负荷有冶炼电弧炉[2]和电力机车[3]，电力用户中单相负荷在三相系统中的不均衡分配也是导致三相电压不平衡的主要原因之一。三相电压不平衡会影响电气设备的正常运转[4，5]，并增大电网的电能损耗[6，7]，因此，三相电压不平衡度是电网电能质量考核的主要指标之一。国家标准《电能质量 三相电压允许不平衡度》明确规定，在正常情况下电网各级电压的三相不平衡度不大于2%，每个用户在公共连接点引起的三相电压不平衡度不得超过1.3%。因此，如何估算不平衡度是贯彻国家标准、提高电能质量的基础。

不平衡度是按照三相电压或电流相量的负序分量来定义和测量计算的[8，9]，在工程实用计算中多有不便，因而出现了多种不平衡度的工程计算方法，以期避免繁琐的复数运算。文献[5，10]给出了利用三相电压幅值直接计算三相电压不平衡度的公式；文献[11]则总结了现有国内外关于不平衡度工程计算的近似方法，比较了各种方法的计算精度和适用范围。这些方法都只需要知道三相电压幅值，因而特别适合实际系统的实测分析。但是，在三相系统设计与理论分析过程中，往往只知道三相负荷功率，此时该方法就变得更为繁琐。

文献[1，5]也给出了单相负荷引起的三相电压不平衡度与单相负荷容量的关系，但对于任意的三相不对称负荷而言，目前尚未建立一套简便的三相电流或电压不平衡度与负荷相间功率的直接对应关系。

本文通过引入负荷序容量的概念，推导出了一套三相不平衡度与负荷相间功率的直接对应关系，简化了三相不平衡度的计算过程，特别适合三相三线不对称系统在设计规划阶段的比较分析与估算。

1 三相负荷的序容量及其计算

1.1 三相负荷电流的序分量

为了分析方便，假设负荷接入点(即PCC点)的电网电压正弦对称且为额定值，即：

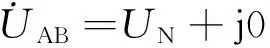
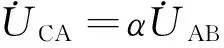
(1)

式中，UN为PCC点三相线电压额定有效值，α和α2为相位变换算子：

设有一个三相不对称负荷，如图1所示。若规定感性负荷无功功率为正，容性负荷无功功率为负，则各相负荷复功率可表示如下：

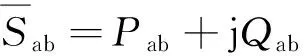
(2)

从公共连接点(PCC)来看，负荷三相总功率为

PL=Pab+Pbc+Pca

QL=Qab+Qbc+Qca

(3)

根据复功率的定义，三相负荷的相间电流为

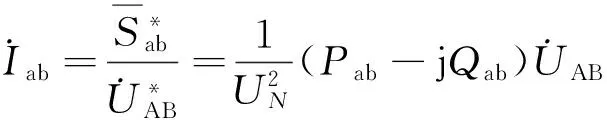
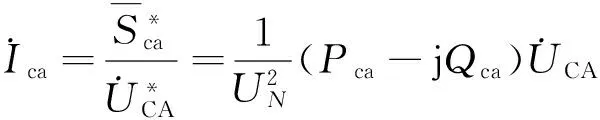
(4)

式中，上标*表示共轭复数。于是，三相负荷的线电流为

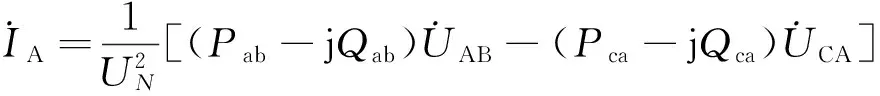
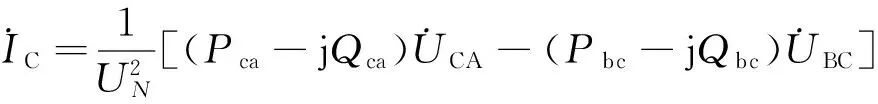
(5)

根据对称分量法，三相负荷线电流的正序分量和负序分量可分别计算如下：

(6)

(7)

将式(5)代入式(6)，可得以负荷功率表示的正序电流分量表达式：

(8)

于是，三相不对称负荷的正序电流有效值为

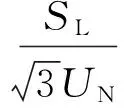
(9)

将式(5)代入式(7)，可得以负荷功率表示的负序电流分量表达式：

(10)

式中

于是，三相不对称负荷的负序电流有效值为

(11)

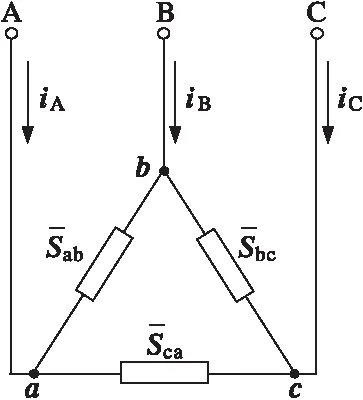
图1 三相不对称负荷连接示意图Fig.1 Connection diagram of three-phase asymmetric load

1.2 三相负荷的序容量

根据式(9)和式(11)所示的三相不对称负荷的正序电流分量和负序电流分量表达式，可定义三相负荷的序功率如下。

定义1三相不对称负荷的正序容量定义为

(12)

式中，I1为三相不对称负荷在正弦对称电压源供电条件下的正序电流分量，UN为PCC点三相线电压额定有效值。其中，PL.1定义为正序有功功率，QL.1定义为正序无功功率：

PL.1=PL=Pab+Pbc+Pca

QL.1=QL=Qab+Qbc+Qca

(13)

上式表明，在不含零序分量的三相配电系统中，三相负荷正序容量等于三相负荷的总容量。

定义2三相不对称负荷的负序容量定义为

(14)

式中，I2为三相不对称负荷在正弦对称电压源供电条件下的负序电流分量，UN为PCC点三相线电压额定有效值。其中，PL.2定义为负序有功功率，QL.2定义为负序无功功率：

(15)

值得指出，三相负荷的正序容量和负序容量仅仅是对三相负荷本身不对称的一种描述，它并不反映负荷与电源之间的实际交换功率，因此它不同于根据线路电流和电压的正负序分量计算所得的正序视在功率和负序视在功率[12]。

2 三相不平衡度的计算

2.1 三相电流不平衡度的计算

在三相对称电源供电的三相三线制配电系统中，根据三相电流不平衡度的定义，有：

(16)

即三相负荷的电流不平衡度等于负荷的负序容量与正序容量之比。

2.2 三相电压不平衡度的计算

图2为三相不对称负荷的供电系统原理示意图，设三相电源电压正弦对称，无穷大电源至公共连接点的系统等值阻抗为(Rd+jXd)，则由图2可得公共连接点的三相电压表达式：

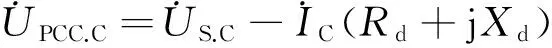
(17)

图2 三相不对称负荷的供电系统原理示意图Fig.2 Three-phase asymmetric load schematic diagramof the power supply system

应用对称分量法，可得公共连接点(PCC)的三相电压的正序分量和负序分量：

(18)

(19)

值得指出，由于假定电源电压对称，故上式中电源电压的负序分量为0。

根据三相电压不平衡度的定义：

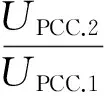
(20)

式中，Id为公共连接点的系统短路电流，并考虑到Id>>I1。设Sd表示公共连接点的系统短路容量，则上式可改写为

(21)

即在三相对称电源供电的三相三线制配电系统中，由三相不对称负荷在公共连接点引起的三相电压不平衡度等于负荷的负序容量与公共连接点的系统短路容量之比。

式(16)和式(21)表明，三相不对称负荷引起的三相电流或电压不平衡度主要取决于负荷的负序容量。在推导负荷的负序容量时，假设PCC点电压对称恒定。实际上，由于电源容量有限，当三相不对称负荷接入电网运行时，PCC点电压必然会出现不对称现象，从而对三相电流不平衡度的计算结果产生一定的误差，误差大小取决于电源短路容量与负荷容量之比，即负荷短路比SCR。附录中的分析表明，在有限容量电源条件下，三相电流不平衡度的相对计算误差满足下式关系：

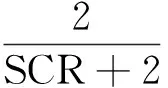
(22)

可见，SCR越大，误差就越小。一般情况下，SCR大于20，此时三相电流不平衡度的计算误差小于10%。因此，上述假设和简化计算是可行的。

2.3 三相电压不平衡度与电流不平衡度的关系

综合式(3)、(12)、(13)、(16)和(21)可得：

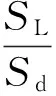
(23)

式中，SCR为PCC点的负荷短路比，即系统短路容量与负荷容量之比。式(23)表明，由三相不对称负荷在公共连接点引起的三相电压不平衡度与负荷电流的三相不平衡度成正比，与负荷的短路比成反比。

3 算例

下列算例充分说明了利用上述定理计算三相不平衡度的方便性和简洁性。

算例1单相负荷设在ab相间连接一个单相负荷Sab，求该负荷的三相电流不平衡度及其在某公共连接点(设负荷短路比SCR=50)引起的三相电压不平衡度。

由于是单相负荷，则：

于是，由负荷条件和式(12)～(15)可得：

PL.1=Pab

QL.1=Qab

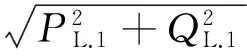
于是，由式(16)可求出三相电流不平衡度：

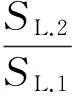
由式(23)可求出三相电压不平衡度：

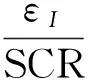
对于两相负荷，则：

于是，由负荷条件和式(12)～(15)可得：

PL.1=2Pab

QL.1=2Qab

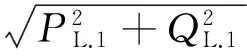
于是，由式(16)可求出三相电流不平衡度：

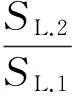
由式(23)可求出三相电压不平衡度：

算例3三相不对称负荷设有三台低压单相负荷[1]，其参数如下：

负荷Ⅰ：7.6 kVA，cosφ=1.0；

负荷Ⅱ：7.6 kVA，cosφ=0.866；

负荷Ⅲ：7.6 kVA，cosφ=0.707

求这三台单相负荷接于不同相间时的6种方式下(见表1)的三相电流不平衡度。该文献采用常规计算方法，过程较为复杂繁琐。下面以方式1为例说明本文所提方法的应用，为了方便，在下列算式中略去变量单位。

按照方式1的规定，分别有：

于是，由负荷条件和式(12)～(15)可得：

PL.1=7.6+6.582+5.374=19.556

QL.1=0+3.8+5.374=9.174

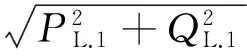
PL.2=(7.6-2×6.582+5.374-

QL.2=(-2×3.8+5.374+

于是，由式(16)可求出三相电流不平衡度：

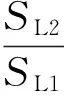
假设低压母线处系统三相短路容量为1 MVA，根据式(21)，由这三台单相负荷引起的低压母线三相电压不平衡度估计为

其它5种方式下的计算结果如表1所示，与文献[1]所给结果是一致的。

表1 6种不同接线方式下的εITab.1 Three-phase current unbalance factorsat 6 different connection modes

4 结语

本文建立了负荷正序容量和负序容量与三相负荷相间功率的关系。正序容量反映了三相负荷的大小，而负序容量反映了三相负荷相间功率的不平衡程度。负荷负序容量与正序容量之比为负荷电流不平衡度，而负序容量与系统短路容量之比表征了由该不对称负荷引起的三相电压不平衡度。算例的演算过程表明，本文算法简化了三相不平衡度的计算过程，在三相三线制不对称负荷供电系统的设计规划中使用极其简便。

[1] 肖湘宁. 电能质量分析与控制[M]. 北京：中国电力出版社，2004.

[2] 李鹏，石新春，梁志瑞，等(Li Peng，Shi Xinchun，Liang Zhirui，etal). 对电弧炉平衡化补偿实用公式推导及验证(Deriving and verifying a practical formula of balancing compensation for arc furnace)[J]. 电工技术学报(Transactions of China Electrotechnical Society)，2001，16(1)：77-80.

[3] 张丽艳，李群湛，余丹(Zhang Liyan，Li Qunzhan，Yu Dan). 阻抗匹配平衡牵引变压器负序分析(Analysis of negative phase-sequence current of impedance-matched balance transformer)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2005，17(6)：80-83.

[4] Von Jouanne A, Banerjee B. Assessment of voltage unbalance[J].IEEE Trans on Power Delivery，2001，16(4)：782-790.

[5] 林海雪. 电力系统三相不平衡[M]. 北京：中国电力出版社，1998.

[6] 程浩忠，艾芊，张志刚,等. 电能质量[M]. 北京：清华大学出版社，2006.

[7] 张五一，张言滨，刘华伟(Zhang Wuyi，Zhang Yanbin，Liu Huawei). 配电网三相负荷不对称的线损分析(Circuit loss analysis of three-phase unbalanced circuit in distribution network)[J].继电器(Relay)，2007，35(7)：24-27.

[8] BG/T 15543-1995，电能质量-三相电压允许不平衡度[S].

[9] 杨淑英(Yang Shuying). 电能质量监测装置研究(Development of electric energy quality monitor device)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2004，16(2)：58-62.

[10]张旭俊(Zhang Xujun). 关于三相电压不平衡时负序电压的计算(Calculation of negative sequence voltage with unbalanced three-phase voltage)[J].华中电力(Central China Electric Power)，1994，7(6)：12-16.

[11]郑国华，张丽(Zheng Guohua, Zhang Li). 电力系统电压的不平衡度讨论(Discussion of voltage unbalance in power system)[J].交通运输工程与信息学报(Journal of Transportation Engineering and Information)，2005，3(4)：45-49.

[12]IEEE Std 1459-2000, IEEE Trial-Use Standard:Definitions for the measurement of electric power quantities under sinusoidal, nonsinusoidal, balanced or unbalanced conditions[S].

附录A

有限容量电源条件下三相电流不平衡度的计算误差分析

当电网为有限容量电源时，可将其等效为一个无穷大电源与内阻抗的串联，如附录图1a所示。设电源等效内阻抗记为ZS，相应的等效内导纳记为YS。设三相相间负荷在额定电压下对应的三相相间阻抗为Zab，Zbc，Zca，相应的导纳为Yab，Ybc，Yca。

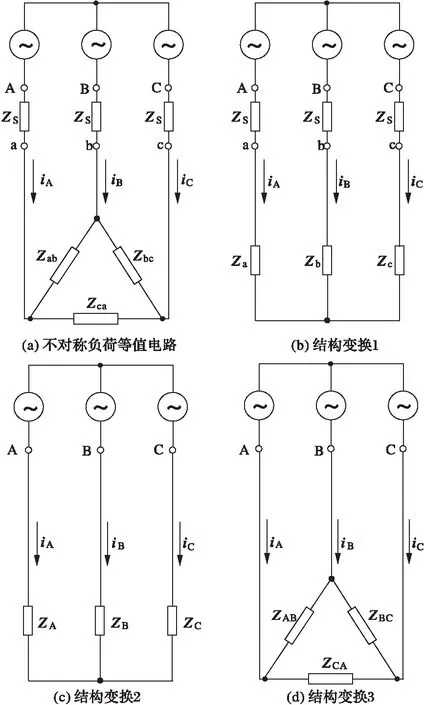
图A 有限容量电源下三相电流不平衡度的计算

首先，将三相负荷的三角形等值电路转换为星形等值电路，如附录图1b所示。转换后的三相负荷等值相阻抗计算如下：

(A1)

将负荷阻抗与电源阻抗合并，形成新的负荷相阻抗ZA，ZB，ZC，如附录图1c所示。

ZA=ZS+Za

ZB=ZS+Zb

ZC=ZS+Zc

(A2)

其次，将合并后的星形等值电路再转换为三角形等值电路，如附录图1d所示。转换后的三相负荷等值相间阻抗计算如下：

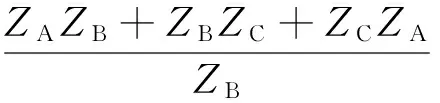
(A3)

将式(A1)和式(A2)带入式(A3)，整理后并以导纳形式表示，可得：

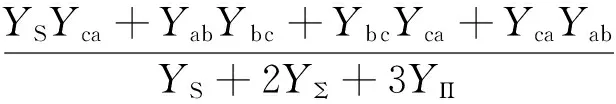
(A4)

其中

YΣ=Yab+Ybc+Yca

(A5)

由式(A4)可得

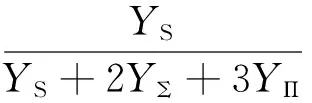
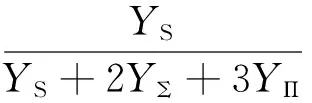
(A6)

由正文中式(14)、(15)和(16)可有：

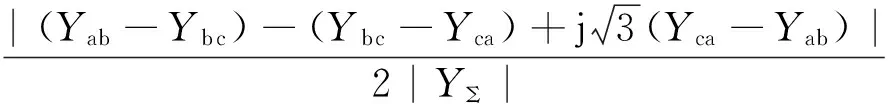
(A7)

若不考虑有限容量电源的影响，则

εI.1=

(A8)

若考虑到有限容量电源的影响，则

εI.2=

(A9)

将式(A6)代入式(A9)，整理可得

(A10)

因此，由于忽略电源阻抗影响而引入的相对误差为

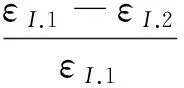
(A11)

负荷短路比可表示为：

(A12)

根据式(A5)和(A11)，有如下关系：

(A13)

由于短路比SCR较大(一般为20～100)，将式(A12)代入式(A11)并化简，可得：

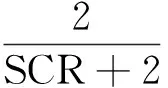
(A14)

关于外文字符的字体

1.正体外文字母的常用场合

a.计量单位和SI词头符号。

b.数学式中的运算符号和缩写号，如:微分号d，有限增量符号Δ，变分号δ，极限lim，行列式det，最大值max等。

c.其值不变的数学常数符号：圆周率π，自然对数的底e，虚数单位i(电工中常用j)。

d.量符号中为区别其他量而加的具有特定含义的非量符号和非变动性数字符号角标，如势能EP，宏观总截面Σtot；转置矩阵AT等。

e.仪器、元件、样品等的型号、代号。

2.斜体外文字母的常用场合

a.用字母代表的数、一般函数及统计学符号等，如：x，y；ΔABC；f(x)；概率P，均数x。

b.量符号和量符号中代表量或变动性数字或坐标符号的角标字母，如：体积V，雷诺数Re，能谱角截面σΩ，E，能量Ei(i=1，2，3)，力的x方向分量Fx。

c.矢量和张量符号用黑斜体。

3.化学元素符号均为正体，且首字母大写。

摘编于《中国高等学校自然科学学报编排规范》(修订版)

CalculationMethodofthree-phaseUnbalanceFactorBasedonLoadPower

TONG Xiang-qian， WANG Hai-yan， YIN Jun

(School of Automation and Information Engineering,Xi'an University of Technology, Xi'an 710048, China)

A practical method for the calculation of unbalance factor caused by asymmetric loads in a three-phase three-wire distribution system was presented. By introducing the term of sequence capacity of an asymmetric load, the current unbalance factor is the ratio of negative-sequence capacity to the positive-sequence capacity of the load, and the voltage unbalance factor at the point of common coupling is the ratio of negative-sequence capacity to the short-circuit capacity of the distribution system. The functional relation between the sequence capacity and the phase-to-phase power of the load was established to simplify the calculating process of unbalance factor. Examples show that the propose method is simple and convenient, and especially suitable for the unbalance factor assessment at the plan stage of industrial distribution systems.

three-phase sequence capacity； three-phase unbalance factor； unbalanced loads； power quality

TM714

A

1003-8930(2011)02-0024-07

2009-12-22

2010-04-06

陕西省重点学科建设专项资金资助项目

同向前(1961-)，男，博士，教授，研究方向为电力电子技术在电力系统中的应用、电能质量的测试分析与控制。Email:lstong@mail.xaut.edu.cn

王海燕(1980-)，女，博士研究生，研究方向为电力系统分析与电力电子控制。Email:wanghaiyan@xaut.edu.cn

尹 军(1979-)，男，硕士，助教，研究方向为配电系统的测量与保护。Email:yyinjun@xaut.edu.cn