数学教学应重视开放性应用题的探索

■何少军

数学教学应重视开放性应用题的探索

■何少军

数学开放性应用问题是新课程的一个重要教学理念，也是评判新课程教学改革成功与否的一个依据。数学开放题在社会各个领域的广泛应用，已使数学成为一种文化。新课程要求数学教学在以人为本的视域下，对开放性应用题的背景、策略、功能进行分析、探究与凝练，发挥开放性应用题的独特功能，培育中学生科学素养与创新思维，进而壮实学生成长的根基，提升学生生命的高度，实现数学教学课程目标。

中学数学；开放性应用题；课程标准

当下，中学数学传统的“一题一答”式教学设计与教学策略已经不能适应新课程标准。那种死记题型，缺乏创意的“功利性”应试教学策略，禁锢了学生的数学思维，削弱了学生解决实际问题的能力，阻碍了学生可持续发展的路径。这种为了一抹功利的传统应试数学教学策略以及对数学课程标准的片面理解与盲目执行，只会将栋梁之才培养成一支完美的牙签。因此，数学教师一定要清醒地跟进、理性地匡正，切实开展数学开放性应用题的分析、探究与凝练。

1 应重视开放性应用题有效设计的背景

当今社会数学在各个领域应用的空前广泛性使数学已经成为一种文化。马克思说过：“每个人的自由发展是一切人的自由发展的条件。”实现全面、协调、可持续的人才发展观从来就是一个家庭的核心问题，也是每位学生家长关注的焦点，更是贯彻教育改革方针的现实考量。为此，数学教师必须重视数学开放性应用题设计的现实背景，在以人为本的视域下，创新设计一些学生感兴趣、与学生生活密切相关的材料或开放性应用题，选择适当的教学时机，以灵活的方式渗透到教学中去，将所学知识融会贯通，不受定势的影响，不受传统的束缚，从多角度、多因果、多方位、多渠道地解决问题，为学生成长发展提供思考、探索、发现和创新的最大空间，为学生提供全面自由发展和健康成长的终极关怀。

2 应重视开放性应用题有效解决的策略

数学教学中，通常将条件不完备、结论不确定，或者解决问题的方法不唯一的并与实际生活生产相关联的问题称之为开放性应用题。数学开放性应用题由于具有与传统封闭题不同的特点，即问题结构的开放与解决问题策略的开放，同时其本身也具有开放性，能够由这个问题引申、变化出新的问题。正因为这类开放性应用题具备这些特点，数学教学中的学习主体也会在解题过程中形成积极探究和创造的心理态势，对数学本质产生一种全新的领悟。为此，数学教师在教学中要十分重视开放性应用题有效解决的策略。

【例】今有六边形钢架ABCDEF，由6条钢管绞接而成（图1）。为使这一钢架稳固，试用另外3条钢管连接，使其固定不能活动。问有多少种不同的连接方法？

【分析】这类开放性应用题，实际可以通过构造数学模型，把它转化成数学结构。即上例可转化为：六边形ABCDEF任添3条对角线后使其固定，有多少种添法？

解上述问题的方法很多，如果没有一个良好的解题策略，很难得出一个完美的答案。为了不遗漏答案，在解题时首先可以计算出所有添法（不考虑固定问题）；然后再考虑任添对角线是否可以分类，各类的每种情况是否固定，从而得到问题的解决。

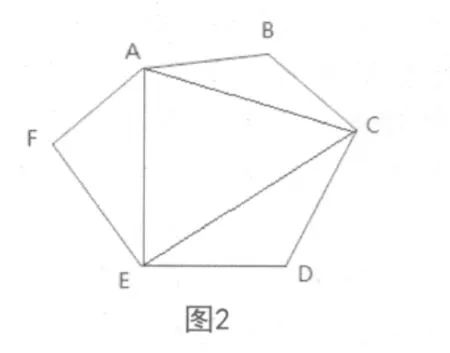
1）从3个顶点出发，且各顶点处有2条，有2种情况，即ΔACE、ΔCDF（图2）。

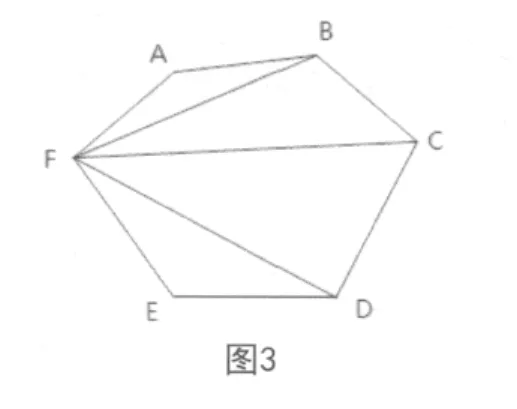
2）从4个项点出发，且：①1个顶点处3条，另3个顶点处各1条，有6种情况（图3）；②2个顶点处各1条，另2个顶点处2条，共有30种情况，其中图4-1、图4-2各有3种，图4-3～图4-6各有6种。

3）从5个顶点出发，且1个顶点处2条，另4个顶点处各1条，共有42种情况，图5-1～图5-7各有6种。

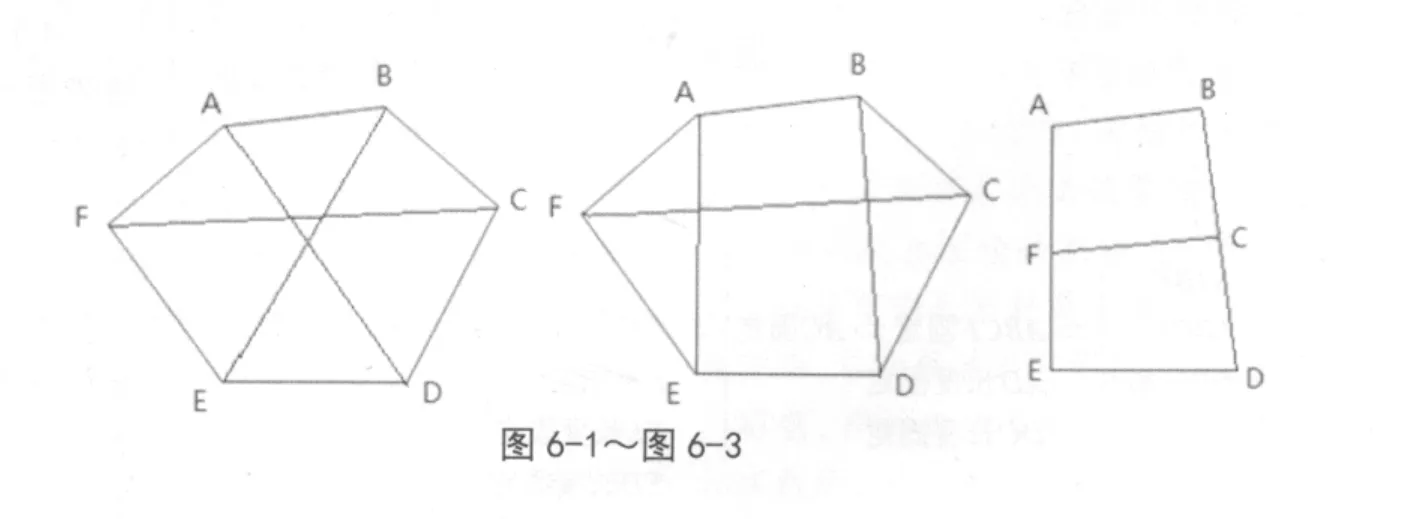
4）从6个顶点出发，有4种，其中图6-1有1种，图6-2有3种。

【分析证明】图2、图3、图4-1、图4-2可根据三角形的稳定性得证六边形的稳定性。

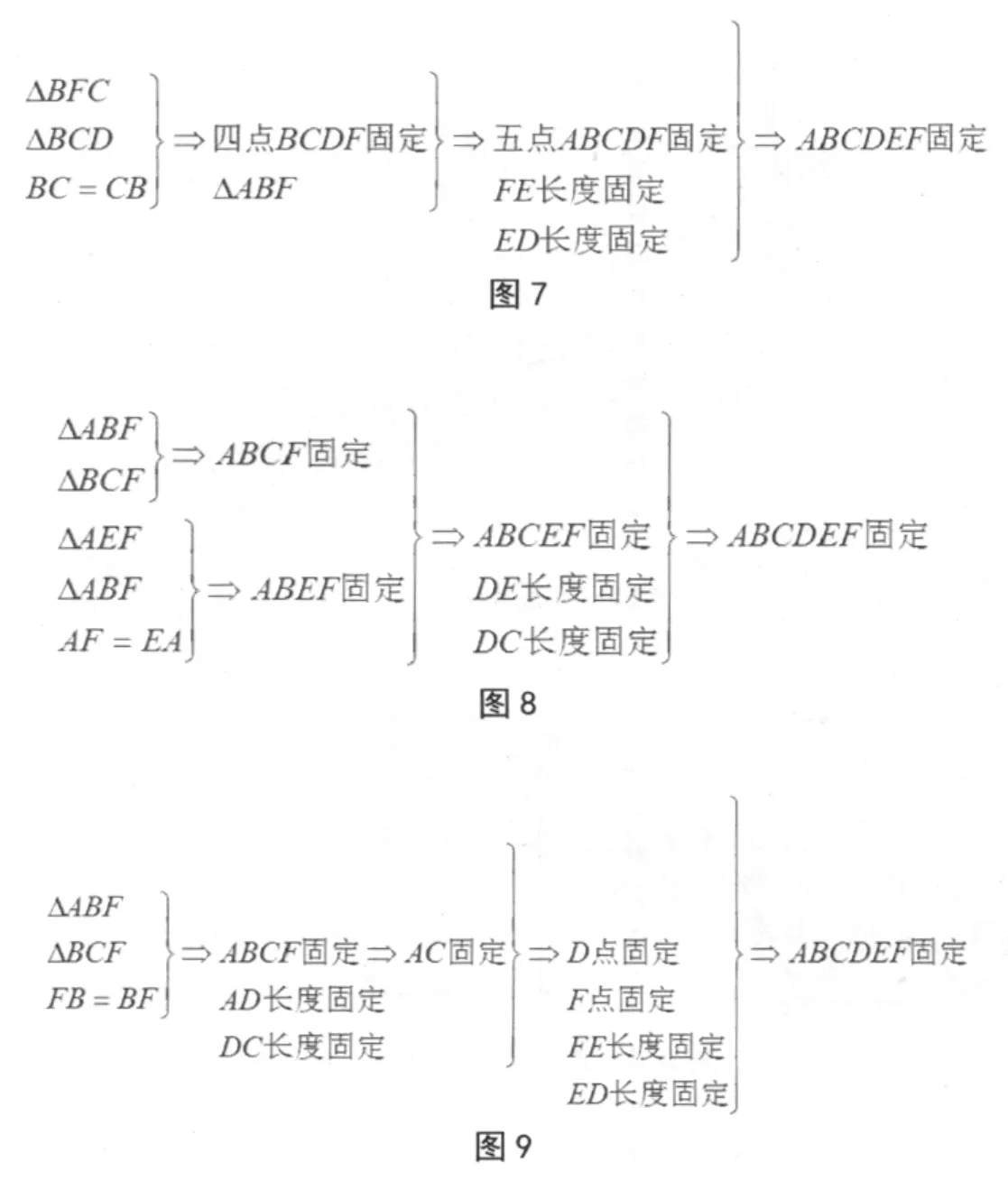
图4-3的证明见图7。图4-4同理得证。

图5-1证明见图8。图4-5、图5-2、图5-5同理得证。

图5-3证明见图9。图5-4～图5-7同理得证。

图4-6证明：因为ADEF为四边形，又因为此四边形是组成六边形的一部分，根据四边形的不稳定性得证。

图6-1证明：因为ABED、BEFC、ADCF都为四边形，所以六边形不稳定。

图6-2证明：因为ABE、CDE都为三角形，由于三角形的稳定性可把图形画成图6-3，由四边形的不稳定性得证其不稳定性。

以上探讨的各种情况除图4-6、图6-1、图6-2共10种不固定外，其他74种方法都是固定的。因此，使这一钢架稳固，试用3条钢管连接使之不能活动，共有74种不同的方法。

3 应重视开放性应用题有效生成的启示

开放性应用题的有效教学总是在教学实践中动态生成的，对这种教学实践进行总结与凝练，能给人许多有益的启示。

1）开放型应用题有利于培养学生用现代数学的思想，通过观察、比较、分析、归纳等方法去解决数学实际问题。重视开放性应用题的教学不仅能巩固和深化学生所学的知识，也能使学生养成独立思考、勇于探索的习惯。

2）探索是数学的生命线。开放性应用题知识覆盖面大，综合性强，解决方法灵活，有一定深度和难度，它的解决过程本身是一种探索性的活动过程。而且这类问题由于题目各个要素的开放性，能激起学生的积极探索动机，使学生对所学的内容产生浓厚的兴趣。因此，在教学中适时引入这类问题，有利于培养学生的学习兴趣，发展学生的直觉思维、逻辑思维及创造性思维。

3）美国教育家布卢姆说过：“一个带着积极情感学习课程的学生或者比那些对学习材料感到焦虑和恐惧的学生，学得更加轻松，更加迅速。”因此，选择有趣味而熟悉的应用题，使学生容易进入问题的情境，积极参与解题活动，在解决问题中得到最佳发展，也就能得到最佳的学习效果，使学生真正成为知识获取过程的主动参与者，成为课堂学习的主人。

4）开放性应用题有利于师生共同成长。随着数学课改的深入，开放性应用题的有效探索将成为一种趋势，这将对教师提出更高的要求。首先，教师必须具备扎实的基础知识和宽广的知识面，针对课程目标与学生实际，设计出整套开放性问题，然后引导学生揭示客观事物的本质与内在联系，在此基础上为学生生命成长播下开创性的种子，进而壮实学生成长的根基，提升学生生命的高度，实现数学教学课程目标。■

[1]张奠宙,戴再平.中学数学问题集[M].上海:华东师范大学出版社,1995

[2]陈国梁.开放型题及其思维对策[J].数学通讯,2001(01):28

[3]吴长江.高中数学开放性问题[M].上海:上海大学出版社,2003

[4]符美权.基于新课程的中学数学开放性教学模式探索[J].改革与开放,2009(6):125

（作者单位：浙江省诸暨教师进修学校）

10.3969/j.issn.1671-489X.2011.11.084