Chebyshev配置点法解 Volterra型积分微分方程

吴 华, 张 珏

(上海大学理学院,上海 200444)

Chebyshev配置点法解 Volterra型积分微分方程

吴 华, 张 珏

(上海大学理学院,上海 200444)

采用 Chebyshev配点法求解 Volterra型积分微分方程,首先将 Volterra型积分微分方程重新写成一个第二类的线性积分方程组,然后将方程组中的被积函数用 Lagrange基函数展开,再将 Lagrange基函数用 Chebyshev多项式展开,在 L∞范数下作误差分析,最后用数值算例来证明该方法的可行性.

Chebyshev配置点法;积分微分方程;Lagrange基函数;Chebyshev权

由于 Volterra型积分微分方程带有记忆性质,与传统的常微分方程和偏微分方程相比,有着本质区别,因此,该方程的数值求解也更为困难.如何快速高效地求解这类方程,一直受到许多学者的关注.由于当解充分光滑时,用谱方法求出的近似解具有很高的精度,所以谱方法经常被运用到近似计算中.因此,本研究采用 Chebyshev配点法解下述 Volterra型积分微分方程:

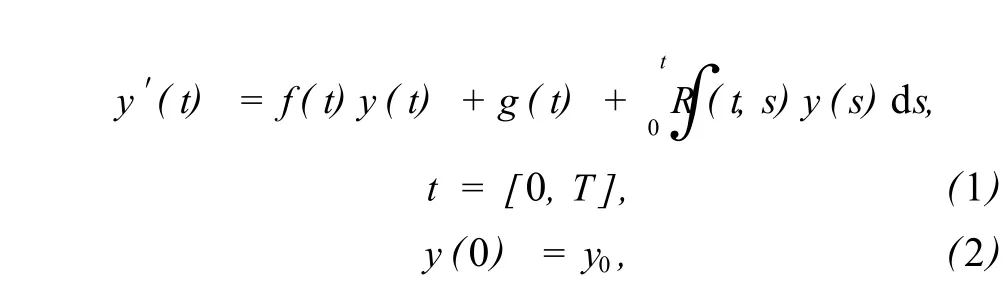
式中,函数 f(t),g(t)和核函数 R(t,s)都是充分光滑的.

为了分析方便,将式 (1)和 (2)转换为定义在[-1,1]上的等价问题.通过变量替换,将式 (1)和(2)转化为

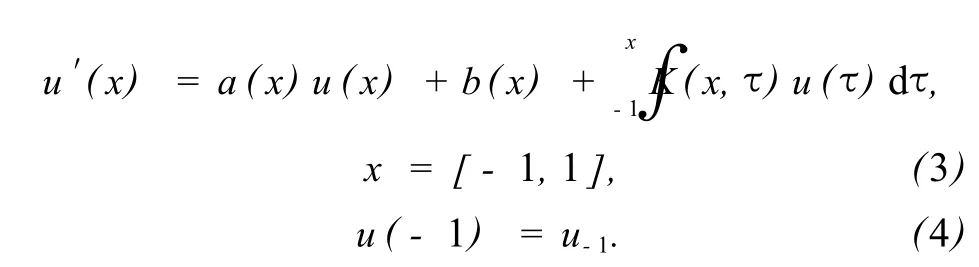
Jiang等[1]把给定的积分微分方程转换成第二类积分方程的方程组,因此,解积分微分方程的主要工作就转变成求解这个积分方程组.Atkinson[2]提出了多种求解第二类积分方程的数值方法,并且作了误差分析.Tang等[3]提出了用 Legendre配点法求解Volterra型积分方程的方法.Chen等[4-5]分别用Chebyshev配点法和 Jacobi配点法求解了带有奇异核的第二类 Volterra型积分方程.Elnagar等[6]用Chebyshev谱方法求解了非线性 Volterra-Hammerstein积分方程.Tian[7]使用谱元法求解Volterra型积分方程,并将谱元法与梯形公式和Simpson公式作了比较,得到谱元法具有更高的收敛阶.Tang等[8]提出了谱处理技术在提高数值解的精度上的应用.另外,其他研究者还提出了获得带有奇异核 Volterra型积分方程和积分微分方程的高阶收敛性质的方法[9-11].

本研究主要是利用 Chebyshev配点法求出Volterra型积分微分方程 (3)和 (4)的数值解.虽然Legendre点在计算中具有很高的稳定性,但是Legendre多项式的权是隐式的,不便于计算.然而,Chebyshev点和权能够直接使用,计算方便.而且Chebyshev多项式能够利用快速傅里叶变换 (fast Fourier transform,FFT),因此,Chebyshev谱方法更常用于工程计算中.一般情况下,Chebyshev谱方法多用于计算带有奇异核的积分方程,而不带奇异核的积分方程经常用 Legendre谱方法来计算.本研究采用 Chebyshev谱方法计算不带奇异核的积分方程,并对该方法作了严格的误差分析,用数值算例证明了其收敛阶.

本研究中,C代表一个与N无关的正常数,但是依赖于所给方程 a(x),b(x),K(x,s)的边界.

1 Chebyshev配点法

类似文献 [1]中的方法,将式 (3)和 (4)写为一种新的形式.记 z=u′,则式 (3)等价于一个关于 z的第二类线性 Volterra型积分方程,即

2 一些预备知识和引理

4 数值实验

出,此方法能达到预期的谱收敛精度.

图 1 数值解与精确解Fig.1 Numer ical solution and exact solution

5 结 束 语

表1 最大误差表Table 1 M aximum error

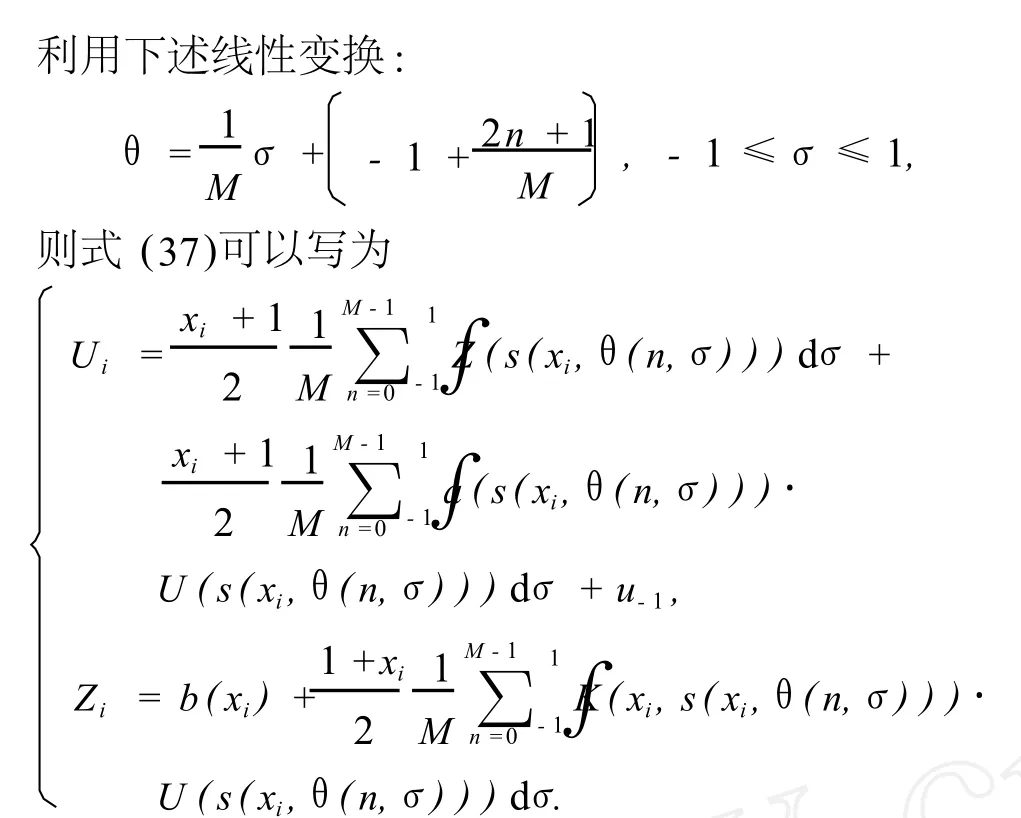
之后,可用 Gauss积分公式来求解上面的方程组中的积分部分.

[1] JIANG Y J.On spectral methods for Volterra type integro-differential equations[J].JComput App lMath,2009,230(2):333-340.

[2] ATKINSON K E. The numerical solution of intgral equations of the second kind [M]. Cambridge:Cambridge University Press,1997.

[3] TANG T,XU X,CHENG J.On spectral methods for Volterra type integral equations and the convergence analysis[J].J ComputMath,2009,26:825-837.

[4] CHEN Y P,TANG T.Convergence analysis for the Cheb yshev collocation methods to Volterra integral equations with aweakly singular kernel[J].SIAM JNumer Anal,2009,233:938-950.

[5] CHEN Y P,TANG T.Convergence analysisof the Jacobi spectral-collocation methods for Volterra integral equations with a weakly singular kernel[J].Math Comput,2010,79:147-167.

[6] ELNAGAR GN,KAZEM IM.Chebyshev spectral solution of nonlinear Volterra-Hammerstein integral equations[J].J Comput App Math,1996,76:147-158.

[7] TIAN H C. Spectral methods for volterrra integral equations[D].Burnaby:Simon Fraser University,1995.

[8] TANG T,XU X.Accuracy enhancement using spectral postprocessing for differential equations and integral equations[J].Commun Comput Phys,2009,5:779-792.

[9] BRUNNER H.Polynomial spline collocation methods for Volterra integro-differential equationswith weakly singular kernels[J].IMA JNumer Anal,1986,6(2):221-139.

[10] DIOGO T,MCKEE S,TANG T.Collocation methods for second-kind Volterra integral equations with weakly singular kernels[C]∥Proceedingsof The Royal Society of Edinburgh.1994,124A:199-210.

[11] TANG T. Superconvergence of numerical solutions to weakly singular Volterra integro-differential equations[J].Numer Math,1992,61:373-382.

Chebyshev-Collocation Spectral M ethod for Volterra Type Integro-D ifferential Equations

WU Hua, ZHANG Jue
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

A Chebyshev-collocation spectral method is developed for Volterra type integro-differential equations.The Volterra type integro-differential equation as two linear integral equations of the second kind is rewrited,and the integrand w ith Lagrange basis functions and the Lagrange basis functions in termsof the Chebyshev polynomialsare expanded.An error analysis isconducted based on the L∞-norm.Numerical results are presented to demonstrate effectivenessof the proposed method.

Chebyshev-collocation spectral method; integro-differential equations;Lagrange basis function;Chebyshev weight

O 175.6

A

1007-2861(2011)02-0182-07

10.3969/j.issn.1007-2861.2011.02.014

2009-10-19

国家自然科学基金资助项目(60874039)

吴 华 (1970～),女,副教授,博士,研究方向为偏微分方程.E-mail:hwu@staff.shu.edu.cn

(编辑:孟庆勋)