基于有限变形理论的能量释放率和 J积分增率形式

宋彦琦, 吕艳伟

(1.中国矿业大学 (北京)理学院,北京 100083;2.普利茅斯大学科技学院,英国 PL4 8AA)

基于有限变形理论的能量释放率和 J积分增率形式

宋彦琦1, 吕艳伟2

(1.中国矿业大学 (北京)理学院,北京 100083;2.普利茅斯大学科技学院,英国 PL4 8AA)

以有裂纹的瞬时位形为参考,建立的增量变形引起的裂纹扩展方程能够更真实地描述裂纹尖端的扩展机制.而真实地描述当前裂纹状态下的增量变形的困难在于,带裂纹尖端的瞬时位形相对于初始位形应满足有关的力学平衡方程.在解决裂纹扩展问题时,基于能量方法的裂纹能量释放率 G和 J积分是一种有效的研究方法.由于经典的微小变形理论引入的裂纹尖端模型解决问题的方法是相对于初始位形的,为得到当前裂纹状态下的增量变形的有关方程,采用能量原理和变分原理,使用有限变形的随体张量表达方式,在瞬时位形基础上,推导裂纹体的能量释放率 G和 J积分的增率G·和J·,建立增量变形的有关方程,从而为研究裂纹尖端的扩展问题提供了新的理论思路.

增量变形;有限变形;能量释放率;J积分;增率形式

裂纹问题与工程结构的破坏和可靠性紧密相关.研究裂纹问题需要用到的断裂力学理论中,裂纹扩展问题十分重要.目前,最常用的裂纹扩展准则是应力型和能量型准则.20世纪 20年代初,Griffith研究了玻璃、陶瓷等材料的脆断问题,采用关于含椭圆孔无限平面介质的弹性力学解作为其理论的基础,并从能量平衡的角度出发,提出了著名的能量释放率理论,导出脆性断裂材料断裂的准则,奠定了断裂力学的基础.

Griffith理论是针对玻璃和陶瓷等理想脆性材料建立的,适用范围有限.Griffith能量释放率准则主要用于线弹性力学,而在弹塑性力学中,则主要采用 J积分守恒定理[1-5].人们常把 J积分作为对Griffith能量释放率准则的一种扩展,其有 3个明显的具有吸引力的特点:①对线弹性行为,其与能量释放率 G相同;②对弹塑性行为,其表征了裂纹尖端区的特征;③J积分与路径无关,可以通过简单的实验得到.

在断裂力学理论及宏观断裂理论研究中,主要着重于应力应变分析,为了数学上的处理方便,仍沿用 Griffith尖裂纹模型,从而导致了在尖裂纹模型下的应力和应变的奇异性.为了消除裂纹尖端奇异性,人们提出了一些新的模型和研究方法,其中比较成功的是由 Eringen发展的非局部理论.尽管这种理论在普遍应用上还存在一定困难,但已显示出它的优越性.陈篪[6]提出恢复裂纹的真实模型的可能裂纹扩展判据.田常海等[7]提出一种复合型裂纹脆断的主应变因子准则.闫相桥[8]在裂纹尖端周围Nadai屈服上考虑断裂参数,提出一个新的断裂准则.王冲[9]提出了一个以转动梯度为基本参数的断裂准则.以上准则对某些材料较为吻合.近年来,一些学者也在裂纹扩展方面做了相关的研究工作[10-14].

在弹塑性断裂分析中,几乎都要用到 J积分准则.但是这种积分守恒性仅在塑性全量理论、小变形以及不发生卸载等条件下成立.很显然,对于裂纹顶端出现大范围屈服时发生的大量的裂纹稳定扩展,J积分准则便无能为力了[1-5].如果摒弃裂纹尖端模型而采用真实的裂纹模型,并且仍然从能量角度来研究裂纹真实的数学物理状态,那么将可能使得经典断裂理论中遇到的这些问题得到解决.

以裂纹前端通常发生的塑性变形作为参考,则原则上引起裂纹或其扩展的是增量变形[15-16].这样,就要在已变形的位形上建立增量变形的有关力学方程.本研究利用有限变形理论中的能量原理和变分原理,考虑含裂纹体真实的物理状态,在含有裂纹物体的瞬时变形的基础上,建立能量释放率 G和J积分的增率G·和J·的形式来描述裂纹体的状态.

1 有限变形理论下的能量原理和变分原理

对于大位移与大变形情况,外力的大小与方向一般在变形渐进过程中发生改变,用功的全量形式来表达是有条件的.物体在空间做三维有限转动时,因最后位形与转动次序有关,故有限转动的功是非保守力性质的.所以,对有限变形与位形功的一般表达式应采用功的增量形式[16].

作用在变形体上的机械力和场力的功增加了变形体的宏观动能和形变能[16],设已知作用在变形体的外力有表面力 P(力 /单位面积)和体力 f(力 /单位质量),考虑无体力矩作用的情况.在拖带坐标系中,以 d a表示界面的微元面积,表示微元体积,ρ为单位体积质量 (变形位形中).变形体中任一点的与速变度形为能 V的,则增外量力功之和率 ,即可表示为动能的增加率从虚功率原理出发,考虑物体运动的每一瞬时,式(2)所表达的能量关系成立.假设某一瞬时,运动达某一状态,以此状态为基准,比较一切可能存在的无穷小相邻状态.

假设在变形后的位形,保持力的大小与方向不变,而给以速度、角速度与应变速率一虚变动,且这些虚变动满足如下协调条件:

2 三维空间中的能量释放率增率形式G·和 J积分增率形式 J·

考虑在三维空间中的一个有裂纹的物体,Σ表示包围裂纹的实曲面,Σ所包含的体积为Ω,如图 1所示.

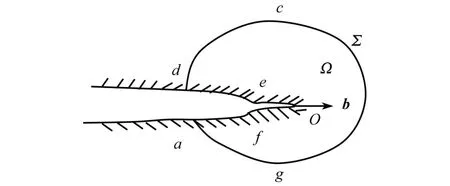
图 1 三维空间的裂纹端部简化模型Fig.1 Sim plif ied model of 3-D crack-tip

2.1 能量释放率的增率形式G·

定义系统势能函数增率为

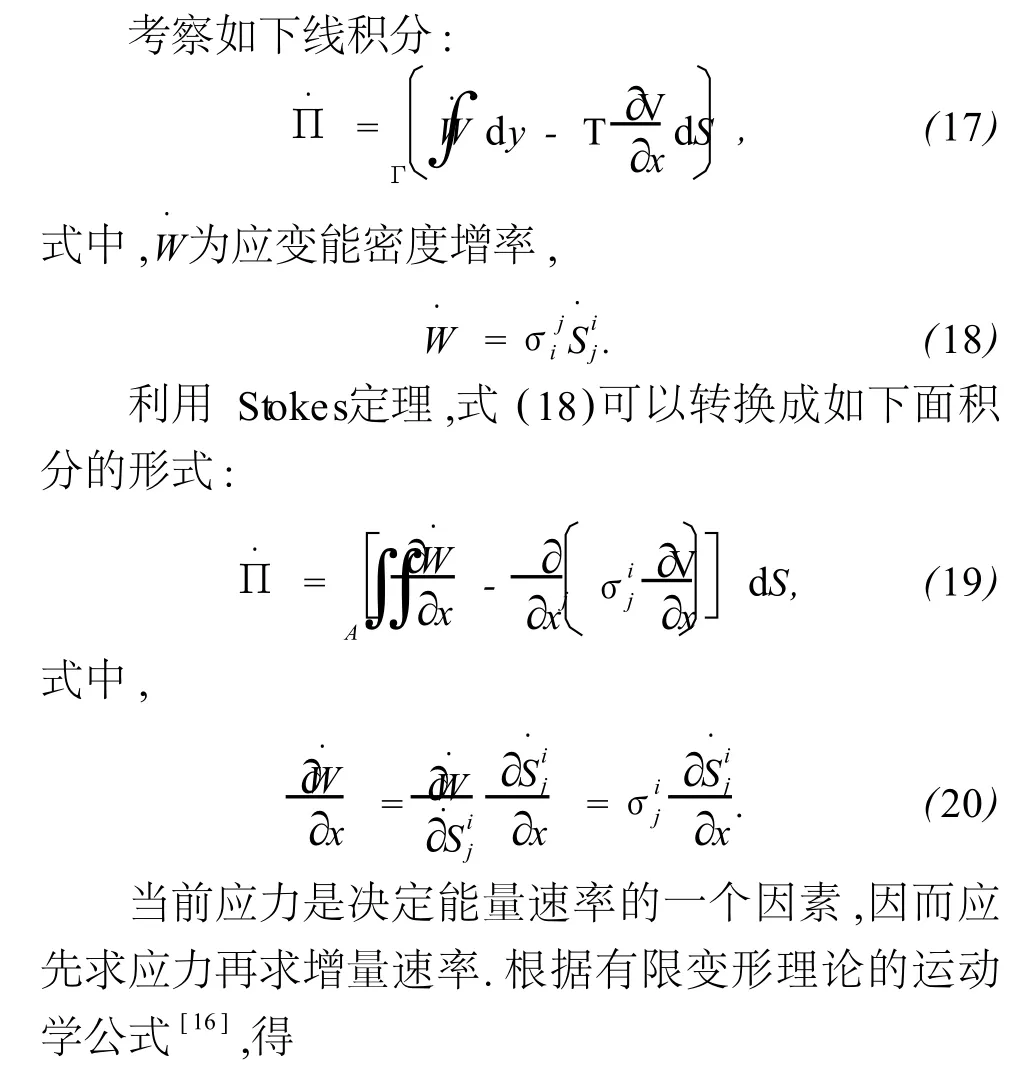
式中,W·为系统单位体积内非保守势能函数的增率,T为曲面Σ上的外力,V为位移场中某点的速度.

设裂纹扩展方向上的单位矢量为 b,裂纹扩展长度为δrb.在时间 t内,保持外力 T不变,则沿着裂纹扩展方向上的势能变化率为

在上述定义中,W·为单位体积内非保守能量势能函数,是点的位置、温度和时间的函数,而不是应变能密度函数的增率.这是由于在实际情况中,裂纹的扩展、裂纹端部小区域一般或多或少会发生不可恢复的塑性变形,存在一定的能量耗散.注意到,Griffith能量释放率准则是建立在初始位形参考上的,其速率并不是在当前位形下的真实速率.事实上,在裂纹扩展问题上,Griffith能量释放率准则并没有给出好的结果.而上文公式是建立在有限变形能量原理和变分原理基础上的,能量释放率增率,适合弹性、弹塑性大小变形情况.

2.2 三维空间中 J积分的增率形式J·

根据上文结果,式 (11)表示系统势能函数增率对裂纹扩展长度δrb变化率.如图 1所示,围绕裂纹端部选择闭曲面 a-g-c-d-O-a,其中裂纹的上下表面de和 ef为自由边界.在该自由边界上,T=0,n·b=0.所以,在裂纹端部的微小区域内,

图 2 简化 2-D裂纹端部模型Fig.2 Simplif ied 2-D crack-tip model

3 结 束 语

本研究应用能量原理和变分原理,考虑裂纹体真实的物理状态,在瞬时位形上推导了裂纹体的能量释放率G和J积分的增率G·和J·,建立了增量变形的有关方程,以能量增率形式真实地描述裂纹状态,为研究裂纹尖端的扩展问题提供了新的理论思路.

[1] HUTCHINSON JW.Singular behaviour at the end of atensile crack in a hardening material[J].JM ech Phys Solids,1968,16:13-31.

[2] RICE J R,ROSENGREN G F.Plane strain deformation near a crack-tip in a power-law hardeningmaterial[J].JMech Phys Solids,1968,16:1-12.

[3] ATLURI SN,NISHIOKA T,NAKAGAKIM.Incremental path-independent integrals in inelastic and dynamic fracture mechanics [J]. Engineering Fracture Mechanics,1984,20:209-244.

[4] YUAN H,BROCKSW.Numerical investigations on the significance of J for large stable crack growth[J].Engineering Fracture Mechanics,1989,32:459-468.

[5] YUAN H,BROCKS W.On the J-integral concept for elastic-p lastic crack extension[J].Nuclear Engineering and Design,1991,131:157-173.

[6] 陈篪.论 J积分和裂纹顶端张开位移间的关系[J].金属学报,1975,11(2):174-182.

[7] 田常海,任明法,陈浩然.复合型裂纹脆断主应变因子准则[J].大连理工大学学报,2001,41(2):139-143.

[8] 闫相桥.一个新的复合型断裂准则[J].哈尔滨工业大学学报,1998,30(4):121-124.

[9] 王冲.断裂力学研究分析新方法——裂面分支平均转动梯度法[D].北京:中国矿业大学,1988.

[10] 杨新辉,栾茂田,杨庆.简化脆性断裂裂尖模型及复合型断裂判据 [J].大连理工大学学报,2005,45(5):712-716.

[11] 赵艳华,徐世烺.Ⅰ-Ⅱ型复合裂纹脆性断裂的最小 J2准则[J].工程力学,2002,19(4):94-98.

[12] 蒋玉川,王启智.复合裂纹扩展的形状改变比能准则[J].四川大学学报,2004,36(3):20-23.

[13] 雷冬,赵建华,蔚夺魁.基于耗散能密度的疲劳裂纹扩展规律研究[J].实验力学,2009,24(1):49-53.

[14] 高鑫,王汉功,康兴无.基于裂尖塑性区的复合材料复合型裂纹断裂准则[J].固体火箭技术,2009,32(1):83-86.

[15] BIOTM A.Mechanicsof incremental deformation[M].New York:John Wiley&Sons Inc,1965.

[16] 陈至达.理性力学[M].重庆:重庆出版社,2000.

Form s of Energy Release Rate and J Internal Increase Rate Based on Fin ite Deformation Theory

SONG Yan-qi1, LÜ Yan-wei2
(1.School of Science,China University of M ining and Technology(Beijing),Beijing 100083,China;2.Faculty of Science and Technology,University of Plymouth,PL4 8AA,UK)

To study the crack propagation problem,a model in terms of incremental deformation represents the real propagation mechanism by taking instantaneous configuration as a reference. It requires an accurate definition of incremental deformation on a fresh crack.However,it is difficult to make the instantaneous configuration including zones around the crack tip satisfy the relevant equilibrium equationswith regards to the initial configuration.Generally,energy methods such as crack tip energy release rate G and J-integral are powerful in analyzing and solving crack problems.Therefore the focus is on the determination of the form of the increase rate of energy release rate,G·,and that of J-integral,J·,regarding instantaneous configuration.Because the classical theory of small deformation takes initial configuration as a reference,the formulae for G·and J·

are derived by using the energy p rincip le and variational principle in the finite deformation theory in the p resent study.This work provides a new theoretical line for studying crack p ropagation.

incremental deformation;finite deformation;energy release rate;J integral;increase rate form

O 331

A

1007-2861(2011)02-0153-05

10.3969/j.issn.1007-2861.2011.02.009

2010-03-02

国家重点基础研究发展计划(973计划)资助项目(2007CB209402,2010CB732002);国家自然科学基金资助项目 (10302030);中央高校基本科研业务费资助项目(2009QS01)

宋彦琦 (1969～),女,副教授,博士,研究方向为固体力学及工程应用.E-mail:yanqi_song@sina.com

(编辑:孟庆勋)