飞秒脉冲光谱全息记录和再现

邹 华, 阎晓娜, 韩 锋, 梁玲亮

(上海大学理学院,上海 200444)

飞秒脉冲光谱全息记录和再现

邹 华, 阎晓娜, 韩 锋, 梁玲亮

(上海大学理学院,上海 200444)

结合飞秒脉冲光谱全息的记录和再现结构,对其物理过程进行详细的描述,给出再现后输出脉冲在不同波矢方向上的光场表达式.详细讨论记录、读出时对信号、参考和探测脉冲入射角的要求,分析各脉冲在频谱面上的光场分布图像,以及信号、参考及探测脉冲宽度不同对结果的影响.研究结果对超短时间脉冲的整形、再现和存储等信号处理有一定的参考价值.

飞秒脉冲;光谱全息;记录;再现

连续光采用傅氏变换全息方法记录物体的空间频谱信息[1],而脉冲光的光谱全息记录的是物体的时间谱信息,称为脉冲光谱全息.飞秒脉冲光谱全息的概念最早由 Mazurenko[2]提出,克服了波包全息中条纹对比度差的问题.Mazurenko从理论上推导了2D光谱全息的记录和再现,但并没有给出完整的输出场表达式,并且由于在其推导中考虑了光谱器件的时间响应函数,使得整个物理过程变得很不明晰.1992年,基于Mazurenko的飞秒脉冲光谱全息的原理,Weiner等[3]以光谱非选择性介质——热塑料作为记录介质,实现了对飞秒时间脉冲信号的存储、再现以及相关和卷积处理.但并未对记录和再现过程进行详细的理论推导,对实验中涉及到的各脉冲宽度以及入射角都没有讨论.近年来,飞秒脉冲光谱全息技术已经被广泛应用于超短脉冲的整形[3]、超精细飞秒微加工[4-5]、超大容量的飞秒光通信[6-7]等多个领域.

本研究结合飞秒脉冲光谱全息的物理图像,对其记录和读取过程进行了系统的理论推导,得到出射脉冲关于信号脉冲、参考脉冲及探测脉冲的表达式.此外,还对每一步涉及的物理过程进行了详细的说明,并且讨论了信号、参考和探测脉冲入射角之间的关系,以及它们的频宽、脉宽对出射光束的影响.

1 飞秒脉冲光谱全息原理

飞秒脉冲光谱全息和一般的傅氏变换全息一样,也包括记录和再现 2个过程.为了更好地理解双脉冲光谱全息的记录,首先讨论单脉冲通过光谱全息记录装置后在输出面的光场分布,之后再讨论双脉冲光场光谱全息的记录和再现.

1.1 单脉冲的频谱分解

飞秒脉冲光谱全息的记录装置与傅氏变换全息类似,不同的是在输入面放置一个光栅.如图 1所示,x1和 x2分别为入射面和频谱面 (在傅氏变换透镜的前后焦面上),θ和γ分别为单脉冲的入射角和其中心波长的衍射角,f为透镜焦距.反射型光栅 G放在透镜的前焦面上,用来把入射的超短时间脉冲所包含的不同频谱成份,按照光栅方程的约束在空间 x1方向展开;傅氏变换透镜L对空间展开的光场分布进行空间的傅氏变换.根据傅里叶光学,频谱面上的光场为透过光栅 G后的光场空间分布的傅氏变换.

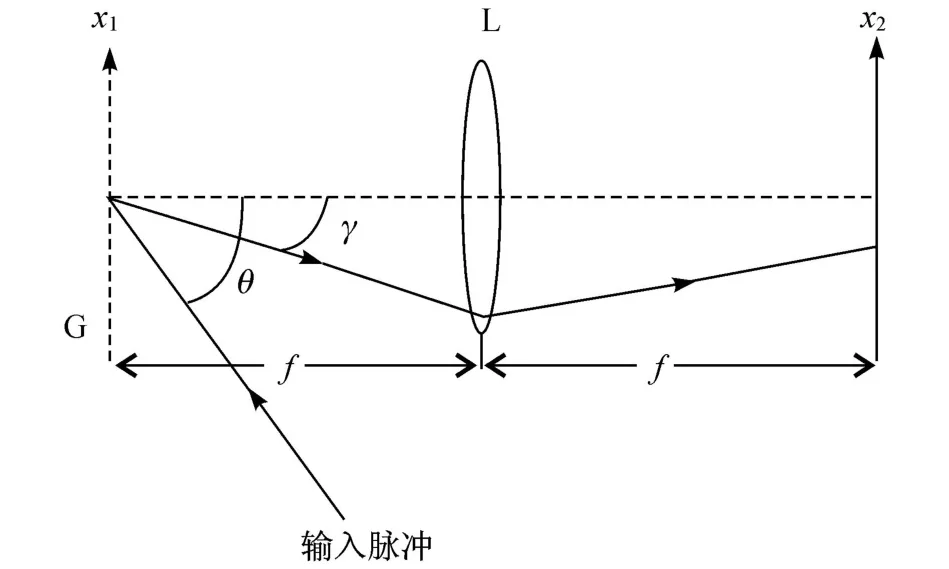
图 1 单脉冲的谱分解装置Fig.1 Spectral decom position of a single pulse

设入射飞秒脉冲的时间为

E(t)=r(t)exp(-iω0t)+c.c.,(1)

式中,c.c.代表复共轭项,ω0为入射脉冲的载频,r(t)为时间包络.由于超短脉冲和其他脉冲一样,是不同频率光场的线性叠加,而输入面光栅 G对不同频率的光场具有不同的衍射作用.因此,引入光场时间包络的频谱函数 R(ω)与时间包络 r(t)为傅氏变换对,具有以下关系:

式中,ω为频谱分量的角频率偏离中心角频率ω0的大小.

当入射脉冲照射到光栅 G时,光栅将脉冲中的不同频谱成分沿 x1方向色散开来.光栅对不同频谱分量的反射率函数为

G(ω,x)=exp(i kβωx), (3)

式中,k=ω0/c为自由空间波数 (c为光速),β=2πc/ω20d cosγ为光栅色散因子,其中 d为光栅周期,γ为入射脉冲中心波长λ0分量对应的衍射角[8].根据光栅方程,γ与入射角θ之间的关系为

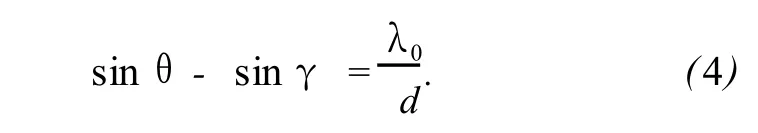
由式 (1)～(3),可得到光栅 G后的衍射光场分布为

由于光栅放在透镜的前焦面上,根据傅里叶光学理论,透镜后焦面上的光场将是透镜前焦面光场V(ω,x)的傅氏变换,该傅氏变换是对空间变量 x进行的,即式中,fx为空频分量.fx与频谱面的空间坐标关系为,其中λ为读出波长,f为透镜的焦距.

由式(6)可知,在频谱面上入射光场分布在以点 x20=kω0βλf为中心的区域附近,入射光场频率偏离中心频率的值越大,相应离中心点的距离越远.x20位置为入射光场频率和入射角度θ的函数.

1.2 双脉冲飞秒光谱全息的记录

要在傅氏变换透镜的频谱面上记录全息,需要有 2个相干光场.假设入射面有 2个入射角分别为θ1和θ2的相干脉冲 Ea(t)和 Eb(t),相应的时间为

Ea(t)=ra(t)exp(-iω0t)+c.c.,(7)

Eb(t)=rb(t)exp(-iω0t)+c.c.,(8)

式中,ω0为两相干脉冲的载频,ra(t)和 rb(t)分别为输入超短脉冲的时间包络.

根据 1.1节讨论,可得 2个相干短脉冲在透镜L后焦面上的场分布为

由式 (9)可知,2个脉冲在频谱面上的光场分布都是δ函数的形式,说明这 2个输入脉冲中的不同频谱分量只能分布在频谱面上的特定位置处.这个特定位置由下式求得:

如果要使 2个脉冲的傅氏变换谱发生干涉从而记录光谱全息,就必须确保 2个脉冲中的相同频率的分量成像在频谱面上的同一位置处,即 2个脉冲谱中的同一频率分量对应的位置 xa,ω1=xb,ω1,将式(10)代入可得

βa=βb=β.

可见,在 2个记录脉冲中心频率相同、光栅周期确定的情况下,要使不同脉冲中同一频率分量在频谱面上相遇,一定要满足 2个光束的入射角θ1=θ2,即 2个脉冲平行入射到光栅上.这是通过光谱全息装置记录光栅时必须满足的前提条件之一.

当来自 2个脉冲的同一频谱分量在频谱面上相遇时,如果是相干光场,则在频谱面上的相应位置处就会发生干涉.产生的干涉条纹被记录在全息介质上,记录的场分布为

U(ω,fx) =ua(ω,fx)+ub(ω,fx), (11)相应的干涉光强分布为

H(ω,fx)=U(ω,fx) ·U(ω,fx)＊. (12)

将式 (9)代入式 (12),可得

在线性记录条件下,经过显影和定影,得到全息介质的复振幅透过率为

t(ω,fx) ∝ H(ω,fx). (14)

由式 (13)和 (14)可知,全息干版的透过率函数是以不同点 xH=kωβλf为中心的干涉条纹.在不同位置处记录不同频率分量的干涉条纹,并且干涉条纹的透过率与此处记录频率有关.由于关心的是光场分布,因此,在下面的讨论中式 (14)取等号,这对结果没有影响.至此,飞秒脉冲光谱全息记录完成.

1.3 飞秒脉冲光谱全息的再现

记录过程结束后,得到透过率函数为式 (14)的全息干版,用如图 2所示的再现装置进行读取.

飞秒脉冲光谱全息的读取装置和 4f系统相似,不同之处是在输入和输出面各放置一个光栅.输入面光栅 G1用来对输入的时间脉冲按照其频率的不同在空间展开,而输出面光栅G2的作用刚好和G1相反,用来把空间展开的不同频率分量合成为一个输出的时间脉冲.假设读出装置中透镜的焦距与记录时相同,同为 f.

图 2 飞秒脉冲光谱全息的再现装置Fig.2 Setup for read ing out the spectral holography

设读出时的探测脉冲为

Ec(t)=rc(t)exp(-iω′0t)+c.c.,(15)

式中,ω′0为读取脉冲的中心频率,rc(t)为读出超短脉冲的时间包络.

由 1.1节讨论可知,探测脉冲在透镜 L1的后焦面、全息干版前的光场分布为

uc(ω,fx)=Rc(ω)δ(fx-kβcω). (16)

由式 (16)可知,探测脉冲通过光栅和透镜 L1后的光场分布在以 xc=kω′βcλ′f′为中心的范围内 ,要使探测脉冲能够读出记录的光谱全息,要求 xc=xH,这样才能保证频率相同的探测光谱场与记录的光谱全息重合.xc=xH意味着有 2个条件必须满足:①读出脉冲中心频率等于记录脉冲中心频率;②读出角度必须等于全息记录时信号脉冲的入射角.

探测脉冲光谱场透过全息干板后的光场分布为

透镜L2的作用是对透过全息干版后的光场进行空间的傅氏变换,变换后的光场分布在光栅 G2的前表面.在如图 2所示的坐标反转情况下,相当于对式 (17)进行傅氏逆变换,得到

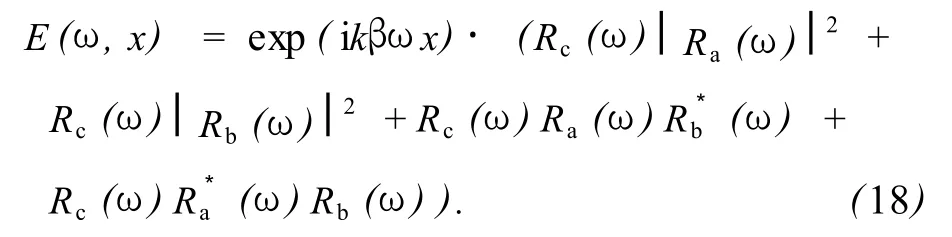
最后,光谱场通过光栅 G2转换为时间分布的脉冲,光栅的作用与入射面光栅 G1刚好相反.出射面光栅的作用可表示为

将式 (18)代入式 (19),得到输出脉冲在时域的表达式为

式 (20)的后 2项可进一步写为

式中,＊代表卷积运算,⊗代表相关运算.

在式 (20)中,本研究所关注的也正是这最后 2个干涉项,即

式中,K1=kc+ka-kb,K2=kc-ka+kb分别表示出射脉冲的波矢方向,ka,kb和 kc分别为信号脉冲、参考脉冲和读出脉冲的波矢量.式 (22)与Weiner实验中给出的结果[3]是相同的.

对式 (21)表示的结果进行讨论,可得如下结论:

(1)如果记录时的参考脉冲和读出时的读出脉冲宽度都很窄,可以表示成δ函数,则在输出端分别得到原信号脉冲的真实再现和原信号脉冲的时间反演;

(2)如果选择参考脉冲为δ型的脉冲,则信号脉冲和探测脉冲的关系为

E(t,x) =rc(t)＊ra(t)+rc(t)⊗ ra(t),(23)

即在输出端分别得到 2个脉冲信号的卷积和相关运算,其中相关运算可以用来实现脉冲的匹配滤波.如果 rc=ra,则是自相关可以用来探测脉冲的变化波形.

2 讨 论

2.1 记录时对信号脉冲和参考脉冲宽度的要求

超短的时间脉冲包含了一定频段的信号,因此,需具体讨论各种频率的信号在透镜后焦面上的分布情况 (见图 3).

选择入射脉冲的中心角频率ω0分量对应于衍射角γ=0,即沿着光轴方向传播,这可以保证利用傅氏变换透镜的中心部分.设角频率的范围为ω1～ω2,根据光栅方程,计算得到角频率为ω′的频率成分成像于透镜后焦面 x′处,即

图 3 输入脉冲中各种频率成分在透镜后焦面的分布Fig.3 D istr ibution of input pulses’d ifferen t frequency at back focal plane of lens

由式 (24)可知,入射光场中偏离中心频率ω0越大的频谱成分,其衍射场在后焦面的位置也离中心位置 x0越远.

角频率范围在ω1～ω2的所有频谱成分在透镜后焦面对应的成像范围为

式中,Δω=ω1-ω2为入射脉冲的频宽.

对于形如 exp(-t2/A2)的高斯型脉冲,其脉宽Δτ和频宽Δω的关系为

将式 (26)代入式 (25),可得

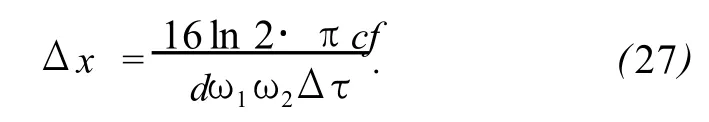
由式 (25)和 (27)可知,成像范围Δx与频宽Δω成正比,与脉宽Δτ成反比.由此可见,要保证信号脉冲中所有的频谱成分都能够被全息介质记录下来,必须使信号脉冲的频宽Δωa小于或等于参考脉冲的频宽Δωb,或者说要使信号脉冲的宽度Δτa大于或等于参考脉冲的宽度Δτb,这样才能保证频谱面上参考脉冲的频谱成分完全覆盖信号脉冲的频谱成分.显然,在再现过程中,也存在类似信息丢失的情况.

2.2 再现时信号脉冲与探测脉冲之间脉宽、频宽的比较关系

在读取过程中,如果探测脉冲的脉宽Δτc小于信号脉冲的脉宽Δτa,则探测脉冲在频谱面上的频谱成分对应的宽度范围将大于信号脉冲的频谱范围,即大于记录全息的频谱范围.此时,读出脉冲能完全读出记录的信息,得到的衍射场分布如式 (20)所示.

如果Δτc＞Δτa,将有部分信号光的频谱分量没有被读取出来,这将导致读取过程中在全息干版上偏离中心频率较大的频谱成分丢失,此时读出场表达式 (17)应改写成

式中,Δω′为探测脉冲的频宽.

这相当于在频谱分布上加上一个以ω0为中心频率的低通滤波器,宽度在Δω′内的频谱分量才能被正常读取出来.如果选取的探测脉冲的脉宽Δτc大于信号脉冲的脉宽Δτa,显然在输出脉冲里会丢失信号脉冲的一些频率成分,最终导致输出脉冲波形的变化,此时式 (20)应改写为

图 4为高斯型的信号、参考和探测脉冲对读取过程中丢失信息的情况进行数值模拟的结果.为了便于讨论,选取式 (22)中 K1方向的输出进行研究.另外,K2方向的输出为关于信号脉冲的共轭项,在强度上和 K1方向的相等.信号脉冲和参考脉冲的脉宽都选为Δτa=Δτb=100fs,探测脉冲分别选 100,120,140和 200fs时的输出脉冲.

由图 4可见 ,当Δτc=Δτa时 ,脉冲宽度最窄.当探测脉冲的宽度增大时,输出脉冲的宽度也增大,这意味着有更多的信号脉冲频率成分在读取过程中丢失.实际上,该结果提供了一种滤波办法,即有意识地利用探测脉冲宽度来过滤掉信号脉冲中的一些高频信号成分.

图 5为式 (23)的数值模拟结果.在模拟中,选择参考脉冲为δ函数,信号脉冲的宽度Δτa=100fs,其频宽Δωa=5.5×1013Hz.这时 ,输出脉冲将只包含信号脉冲与探测脉冲的卷积和相关项.

由图 5可知,如果改变探测脉冲的频宽Δωc,则输出脉冲的宽度也将随之变化.当Δωc=Δωa=5.5×1013Hz时,脉冲宽度最窄,这说明信号脉冲中各种频谱成分被全部读出.随着探测脉冲的频宽Δωc从 5.5×1013Hz减小到2.5×1013Hz,输出脉冲的宽度逐渐展宽,这说明信号脉冲里的一些频谱成分在读出过程中丢失.所选择的探测脉冲频宽越小,输出脉冲的展宽越大,这意味着有更多的信号脉冲频率成分在读取过程中丢失.

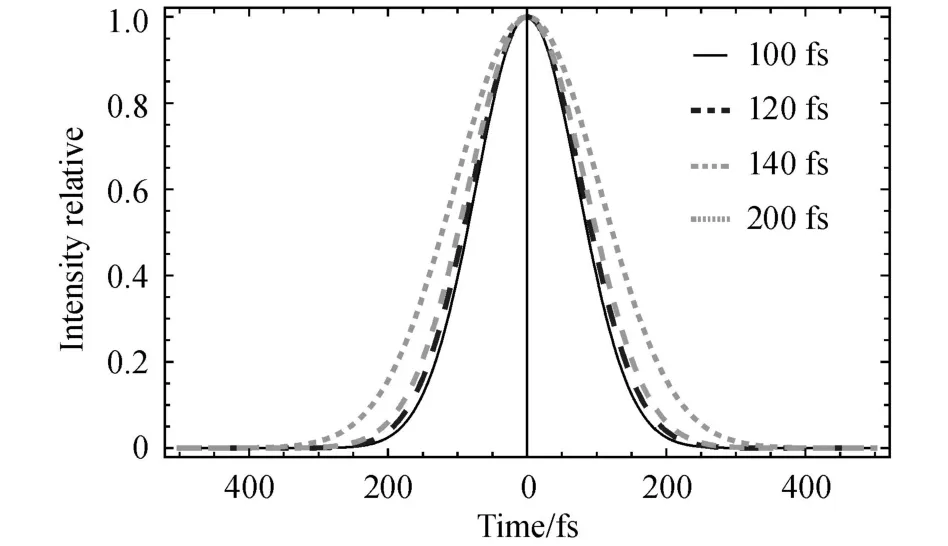
图 4 选取不同Δτc的探测脉冲读取时,输出脉冲归一化强度的时间分布Fig.4 Normalized intensityofoutputpulsewith differentpulsedurationΔτcofthetestpulse inreadoutprocess

图 5 选取不同Δωc的探测脉冲读取时,输出脉冲归一化强度的时间分布Fig.5 Normalized intensityofoutputpulsewith differentbandwidthΔωcofthetestpulsein readoutprocess

3 结 束 语

本研究主要讨论了飞秒光谱全息的 2个主要的步骤——记录和读取,通过具体的理论推导得出了输出脉冲的表达式,并详细分析了信号、参考和探测脉冲的入射角度及脉宽、频宽对输出脉冲的影响.通过合理地选择信号、参考和探测脉冲,可以在输出脉冲中得到信号脉冲和参考脉冲的卷积和相关运算、信号脉冲的原函数和时间反演等.结合光谱全息的理论,讨论了入射角、读出角必须相等的条件,并得到如下结论:为把信号脉冲记录下来,记录时选择参考脉冲的宽度要小于信号脉冲的宽度,且读出时探测脉冲宽度要小于信号脉冲宽度,否则由于读出时丢失频谱分量,输出脉冲会被展宽.本结论对研究及利用超短脉冲光谱全息具有参考价值.

[1] WEINER A M,LEA IRD D E,REITZE D H.Femtosecond spectral holography[J]. IEEE Journal of Quantum Electronics,1992,28(10):2251-2261.

[2] MAZURENKO Y T.Holography of wave packets[J].Appl Phys B,1990,50:101-114.

[3] WEINER A M,LEA IRD D E,REITZE D H,et al.Spectral holography of shaped femtosecond pulses[J].Opt Lett,1992,17:224-226.

[4] KONDO T,MATSUO S,JUODKAZIS S, et al.Femtosecond laser interference technique w ith diffractive beam splitter for fabrication of three-dimensional photonic crystals[J].App l Phys Lett,2001,79(6):725-727.

[5] L I Y,WATANABE W,YAMADA K,et al.Holographic fabrication of multiple layers of grating inside soda-lime glass with femtosecond laser pulses[J].Appl Phys Lett,2002,80(9):1508-1510.

[6] WEINER A M,HERITAGE J P,SALEHI J A.Encoding and decoding of femtosecond pulses[J].Opt Lett,1988,13:300-302.

[7] MENDEZ A J,GAGL IARD I R M,HERNANDEZ V J,et al.Design and performance analysis of wave-length/time(W/T)matrix codes for optical CDMA [J].Journal of Light Wave Technology,2003,21(11):2524-2532.

[8] MARTINEZ O E.Grating and p rism comp ressors in the case of finite beam size[J].Opt Soc Am B,1986,3(7):929-934.

上海大学期刊社网站喜获“上海市期刊十佳网站”提名奖

新年伊始,我校期刊社又传捷报:在 2011年 1月 28日召开的上海市期刊协会三届四次理事会议上,由上海市期刊协会主办的“上海市期刊十佳网站”评选结果揭晓,上海大学期刊社网站荣获 2010年“上海市期刊十佳网站”提名奖.

据悉,此次评选是上海市期刊协会首次举办的网站交流活动,对参评的上海市数十家社会科学和自然科学期刊网站分别从“网站影响力”、“网站栏目设置及内容功能”、“网络管理制度建设及安全”三个方面进行评选.经过初选、复选和公开答辩,再经过理事会无记名投票,最终评选出“上海市期刊十佳网站”及 10个提名奖获得者.

上大期刊社网站创建于 2007年 3月,由期刊社信息化工作室和编辑部网管员二级管理并负责.经过网站工作人员 (兼职)四年的精心设计和辛勤耕耘,目前网站内容丰富,栏目设置科学合理,既为员工即时获取本社各种信息、了解规章制度及期刊编辑、出版的法律法规等提供了方便,也为期刊的作者、读者了解期刊社十种期刊信息、投稿等提供了便捷条件,同时也为作者和编辑提供了重要的交流平台.

上大期刊社网站工作人员将继续努力,争取把网站办得更完善,更好地为编辑、作者和读者服务.

(上海大学期刊社)

Record ing and Readout of Fem tosecond Spectral Holography

ZOU Hua, YAN Xiao-na, HAN Feng, L IANGLing-liang
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

Based on the recording and readout structures of femtosecond spectral holography,the entire physical procedures is depicted,and the mathematical expressions for the output pulse field distribution in different directions is given.The choices of the angles of signal,reference and test pulses,and distributionsof the signal,reference and test pulses on the spectral plane are discussed.Then the influence of signal,reference and testpulses’duration on the outputpulses isdiscussed.The results are useful to the ultrashort pulse signal processing including shaping,storage and reconstruction.

femtosecond pulse;spectral holography;record;readout

O 438.1;O 438.2

A

1007-2861(2011)02-0170-06

10.3969/j.issn.1007-2861.2011.02.012

2009-10-09

国家自然科学基金资助项目(60908007,10974132);上海市重点学科建设资助项目(S30105)

阎晓娜 (1970～),女,副教授,博士,研究方向为信息光学.E-mail:xnyan@staff.shu.edu.cn

(编辑:刘志强)