主成分回归的SPSS实现

郭呈全，陈希镇

（温州大学数学与信息科学学院，浙江温州325000）

主成分回归的SPSS实现

郭呈全，陈希镇

（温州大学数学与信息科学学院，浙江温州325000）

文章结合主成分分析和线性回归分析的原理，利用SPSS15.0的Descriptives、Data Reduction、Linear Regression、Compute Variable模块的功能，把主成分回归的每一步计算过程用SPSS展现出来，并且对结果给出SAS验证。这不仅使学生更好地掌握主成分回归的相关知识，而且可以培养学生灵活使用SPSS软件。

共线性；主成分回归；特征值；特征向量；SPSS

0 引言

在进行多元线性回归分析时，经常会遇到自变量之间存在近似线性关系的现象，这种现象被称为共线性[1]。当共线性严重时，用最小二乘法建立的回归模型将会增加参数的方差，使得回归方程变的很不稳定，有些自变量对因变量影响的显著性被隐藏起来，某些回归系数的符号与实际意义不相符[2]，回归方程和回归系数通不过显著性检验。处理共线性的主要方法有筛选变量法、岭回归法、主成分回归法、偏最小二乘法等。在文献[2]中高惠旋使用SAS软件对处理共线性的主成分回归方法进行了实现，但是很多人只熟悉SPSS操作，SPSS没有直接提供主成分回归的模块，文献[3]虽然也提出使用SPSS进行主成分回归，但是他首先使用了筛选变量法，没能真正体现主成分回归方法提取主成分的优势，而且其操作过程非常繁琐，没有灵活使用SPSS软件模块功能。本文结合主成分分析和线性回归分析的原理，巧用SPSS15.0的Descriptives、Data Reduction、Linear Regression、Compute Variable模块的功能,把主成分回归的每一步计算过程用SPSS展现出来，并且对结果给出了SAS验证。不但得出了正确结果,而且把每一步计算过程完整地呈现出来，这样既有利学生掌握有关方面的知识，还能加深学生对统计软件的灵活使用和掌握。

1 基本原理和计算步骤

1933年，Hotelling提出主成分分析方法，主成份分析的核心思想就是通过降维，把多个指标化为少数几个综合指标，而尽量不改变指标体系对因变量的解释程度。W.F. Massy于1965年根据主成份分析的思想提出了主成份回归。如今主成份回归方法已经被广泛采用，成为回归分析中解决多重共线性比较有效的方法。

设Y=（y1，y2，…，yn），假设X设计矩阵已经中心化，记λ1≥λ2≥…≥λp为X'X的特征根，Φ=(φ1，φ2，…，φp)为对应的标准正交化特征向量。主成分回归的计算步骤是：

（1）为了使结果不受量纲的影响，先把原始数据进行标准化；

（2）求X'X的特征值和对应的标准正交化特征向量；

（3）做回归自变量选择。最大的特征值对应的特征向量即为第一主成分的系数，第二大的特征值对应的特征向量即为第二主成分的系数，以此类推。取几个主成分取决于主成分对因变量的解释程度。如果前i个特征值之和与所有特征值之和的比达到一定的程度比如85%时，就可以认为这些主分就能代替所有的自变量体系。剔除对应的特征值比较小的那些主成分。

（4）做正交变换Z=XΦ，获得新的自变量；

（5）将剩余的成分对因变量进行普通最小二乘回归，再返回到原来的参数，便得到因变量对原始变量的主成分回归。

总结这些步骤可以看出：主成份回归解决多重共线性问题是通过求特征值和特征向量达到降维来实现的。因为在降维前指标之间的多重共线性可能是由于某个指标或者少数指标所包含的信息与其他指标所包含的信息之间的相关性引起的，通过降维的处理我们提取出了主成份，就像是把指标体系所包含的信息分了类，某一大类由一个主成份来表现，这样就消除了产生多重共线性问题的根源：信息的交迭[4]。

2 SPSS对计算过程的实现

利用文献[1]中的外贸数据：因变量Y为进口总额，自变量X1为国内总产值，X2为存储量，X3为总消费。为了建立Y对自变量X1，X2和X3之间的依赖关系，收集了11组数据见表1。

表1

2.1 数据标准化

执行：Analyze→Descriptives Statistics→Descriptives，将变量y，x1，x2，x3选入Variables的对话框中，选定Save standardized values as variables，即将标准化后的数据作为变量保存。见表2。

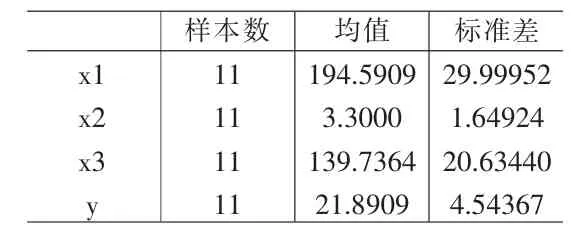
表2 描述性统计量表

描述性统计量表中显示各变量的样本数（N）、均数（mean）和标准差（Std.Deviation），以便于对中心化后的自变量进行完主成分回归后还原为原始变量。

2.2 共线性诊断

共线性就是对自变量观测数据构成的矩阵X'X进行分析，使用各种指标反映自变量间的相关性。进行共线性诊断的方法有很多种，目前较为常用的诊断方法有：条件数（condition index）、容忍度Tolerance（或方差膨胀因子（VIF））、特征根（Eigen value）分解法。

（1）条件数：是指X'X的最大特征根与最小特征根之比k=λ1/λp，它刻画了特征值差异的大小。一般情况下k<100，则认为复共线性很小；100≤k≤1000认为存在中等程度的复共线性；若k>1000则认为存在严重共线性。

（2）容忍度：以每个自变量作为因变量对其他自变量进行回归分析时得到残差比例，用1减去决定系数来表示(1-R2)，越小说明共线性越重，T<0.1时共线性非常严重（陈希孺）。由此方差膨胀因子（VIF）：定义VIF=1/T，VIF越大，说明共线性越严重。

（3）特征根分解法：对自变量进行主成分分析，若相当多维度的特征根为0，则共线性严重。

本例共线性诊断操作步骤如下：执行：Analyze→Regression→Linear，在Dependent中选择导入，在Independent中导入Zx1，Zx2，Zx3，在statistics中选中Colinearity statistics，其它选项默认，得表3。

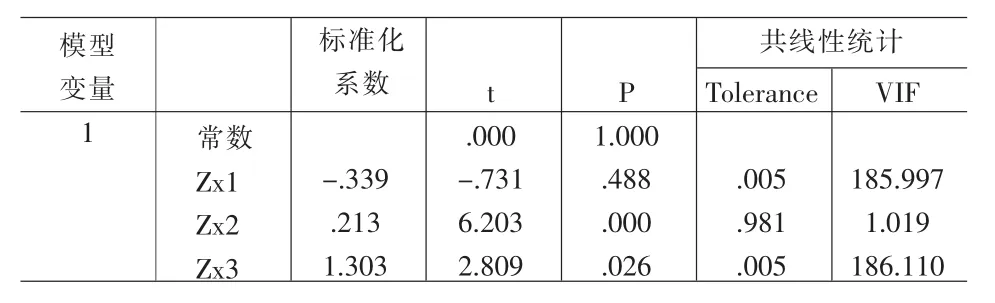
表3 回归系数和共线性统计量

表3给出线性回归方程中回归系数的估计值和共线性统计量，表中ZX1和ZX3容忍度都为0.005<0.1，并且其方差膨胀因子VIF都很大，说明它们之间存在严重的共线性。

表4 共线性诊断指标

从表4可以看出，条件数1.999/0.003≈666.33，故共线性程度较严重。从方差百分比上看，ZX1和ZX3变量间也存在明显相关性。

2.3 主成分分析

执行：Analyze→Data Reduction→Factor，选定标准化后的变量Zx1，Zx2，Zx3进入Variables中，Extraction中的选项，method选用principal components，Analyze选用covariance matrix，在提取主成分的Extract中选用Number of factor并在后面的框中填入3，提取三个主成分。在Scores中选择Save as variables；在method中选择reg；不进行旋转，结果输出如表5。

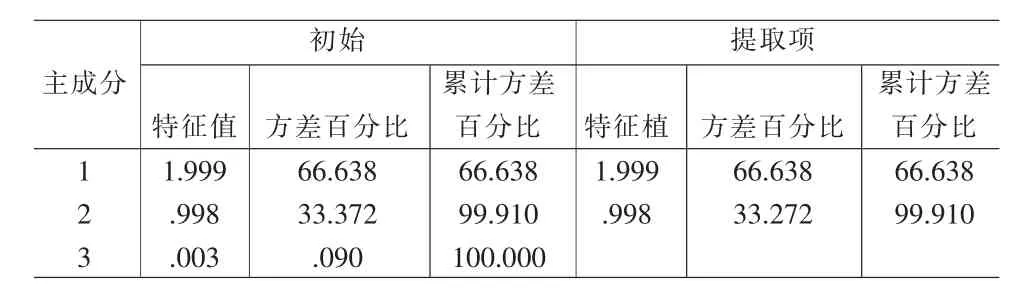
表5 主成分提取汇总表

表5显示三个特征值分别为λ1=1.999，λ2=0.998，λ3= 0.003，前两个特征值的累计贡献率达到99.91%，因此剔除第三个主成分，相应的因子载荷矩阵如表6。

表6 得分矩阵

2.4 求特征向量和主成分

前两个特征值λ1=1.999，λ2=0.998，对应的标准正交化特征向量分别为：

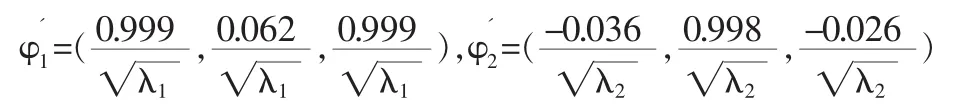
下面使用Compute Variable模块的功能，计算第一和第二主成分。

执行：Analyze→Transform→Compute Variable，在Target Variable中输入Z1，在Numeric Expression中计算公式为：Z1=FAC1_1*sprt(1.999)，单击OK产生新变量Z1，同上得：

Z2=FAC2_1*sqrt(0.998)，于是得：

输出变量结果如表7。

表7 主成分表

2.5 线性回归

对第一主成分Z1和第二主成分Z2做关于中心化因变量Zy的最小二乘回归分析。

执行：Analyze→Regression→Linear，在Dependent中选择Zy导入，在Independent中导入Z1和Z2，做最小二乘回归。见表8。

表8 回归系数

回归系数估计值为：→β1=0.690，→β2=0.191，常数项近似为零。把上面关系式代入：

Zy=0.69Z1+0.191Z2+7.07E-017，求得：

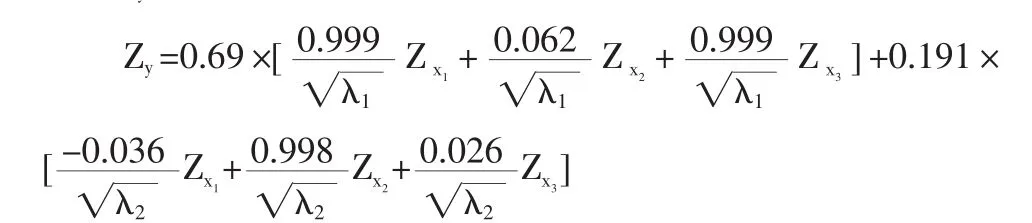
因此，Zy=0.4806Zx1+0.2298Zx2+0.4825Zx3。

y=-9.1057+0.0727x1+0.6091x2+0.1062x3。

3 SAS验证

使用SAS的REG过程，对上述数据做主成分分析，SAS程序如下：

Proc reg data=a outset=out1；

Model y=x1-x3/pcomit=1,2 outvif；

Proc print data=out1；

Run后输出如下结果：

由SAS运行结果可以看出，这个主成分回归中回归系数的符号都是有意义的；各个回归系数的方差膨胀因子均小于1.1；主成分回归的均方根误差是：RMSE=0.55001，虽然比最小二乘的均方根误差（RMSE=0.48887）有所增加，但增加很小。在删去第三个主成分（PCOMIT=1）后的主成分回归方程为：

y=-9.1301+0.7278x1+0.960922x2+0.10626x3

这一结果与我们SPSS处理结果近似相等，进而互相验证了彼此的正确性。

4 结束语

本数据选自文献[1]，在文献[1]中的人工计算结果以及文献[2]通过SAS编程得到的计算结果都与此相同,这说明我们利用SPSS的计算过程与结果是正确的。另一方面,由计算过程可以看出,一道题的计算过程的实现不只是在一个操作菜单的命令下就可以完成,本例用SPSS15.0的Descriptives、Data Reduction、Linear Regression、Compute Variable模块的功能，因此对软件SPSS的使用要求就上升到能熟练运用的高度。本文说明,如果能在多元统计教学的同时注意有关软件的使用，开动脑筋，灵活使用，不但能很好地实现每一步的计算过程，而且还可用来解决更多新问题。这不但有利于学生掌握有关方面的知识,而且加深了对统计软件的使用和掌握,从而达到培养学生灵活应用统计软件SPSS的目的。

[1]王松桂,陈敏,陈立萍.线性统计模型：线性回归与方差分析[M].北京：高等教育出版社，2004.

[2]高惠旋.处理多元线性回归中自变量共线性的几种方法[J].数理统计与管理，2000，20(5).

[3]刘润幸，萧灿培，宫齐等.利用SPSS进行主成分回归分析[J].数理医药学杂志，2001,14(2).

[4]周松青.解决多重共线性问题的线性回归方法[J].江苏统计，2000，（11）.

（责任编辑/易永生）

O21

A

1002－6487（2011）05-0157-03

国家统计局资助项目（LX08081）；浙江省精品课程“统计学概论”和温州大学研究生精品课程“多元统计学分析”资助