基于后验修正bayes决策树模型的保险营销决策方法
聂尔德
(安徽大学国际商学院,合肥230061)
基于后验修正bayes决策树模型的保险营销决策方法
聂尔德
(安徽大学国际商学院,合肥230061)
文章首先在对Bayes决策体系进行细致分析后,提出了保险营销决策模型,并对引起情报价值的状态因素进行分解,以确定在何种自然状态下一般决策较大,使得有针对性地避免措施产生。其次根据多阶段决策原理引入后验信息,为保险企业进行产品试验分析提供理论方法,在此基础上根据一个算例提出修正概率变动趋势与由Bayes矩阵估计出的概率变动趋势的一致性判定准则,以克服以往研究不对后验情报价值具有性进行判定的缺陷。
Bayes决策;后验;保险营销;决策
0 引言
保险业销售的是一种无形商品,随着消费者的自我保护及风险转移意识的增强,这种金融衍生品越来越受到人们的重视和亲睐。根据《国际金融报》统计数据显示:2009年前三季度,全国实现保费收入8580.3亿元,同比增长8.1%,与2009年GDP增速8.7%相近。作为一种商品,必然有生产—销售—售后服务等一系列商业过程,其中对单个保险品种在未来一段时间的市场前景预测工作,是支撑起保险业正常运营的关键。并且同其他商品的营销相比,保险商品的营销更注重主动性,人性化和关系营销[1]。所以在对保险产品进行预测的过程中,更应重视到试验的重要性,从而对原始数据和过去经验进行修正,制定并实施科学、准确的保险营销策略。基于此,文章拟引入后验信息试验,对原始随机决策模型进行修正,并进行精确度测试,并将引入一个算例以达到对实际预测进行指导和对模型进行证明的目的。
1 基于bayes决策的保险营销决策模型
1.1 Bayes决策体系构建及改进
Bayes决策针对的问题是在未来状态不确定的情况下,归纳假设出有若干种可能的状态及相应概率,并依据此进行决策选择或排序。保险产品具有所有商品的共性,会出现一定的市场状态,由于保险需求存在很大的潜在需求,需要一定的策略去激发,那么可以将策略作为手段,状态作为激发的最终目的,但策略—目的的映射关系往往在现实中并不能准确描述和刻度。故只能依据经验和历史数据进行评判(为先验信息下的预测),笔者以bayes体系为基础,确定保险产品市场预测模型。
对于某保险产品X,有决策方案集A={a1,a2,…,ai,…,am},表示有m种营销策略,其中ai为第i种策略;那么决策人员通过市场调查法所确定的未来X产品可能面对的状态,得到状态集θ={θ1,θ2,…,θi,…,θn},表示有n种可能状态,其中θi为第j种市场状态。那么确定状态和确定策略下的交叉收益可由rij表示,为采取i营销策略却又正好出现j市场状态的收益值,那么交叉收益的期望可定义为rijpj。具体可由表1表示。
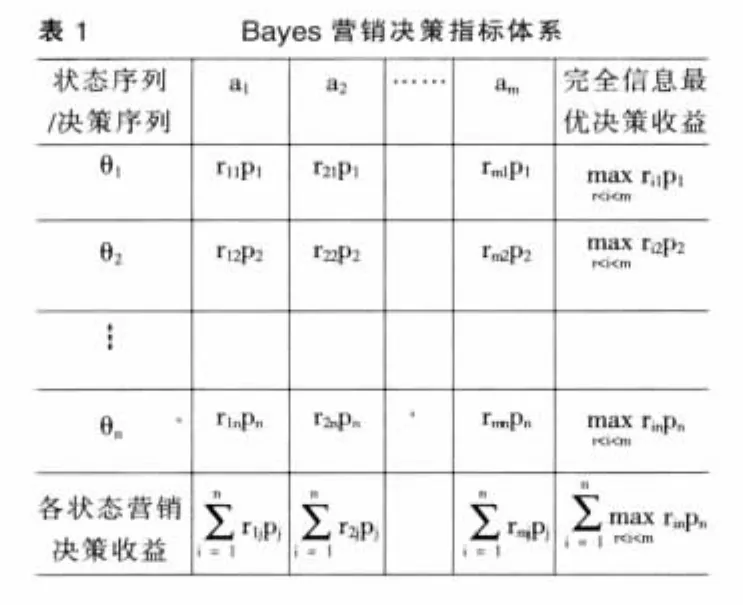
表1种最后一行表示每一种决策在不确定状态集合下可能得到的期望收益(期望损失),往往在制定营销策略时,只选出期望收益(期望损失)的最大值(最小值),进行单一决策,即非A即B得选择。表最后1列表示完全信息最优决策收益(损失),理想状态时,营销决策者完全了解每种状态所发生的时间占比,在既定的概率下,从每个概率区间中选取最优的决策方法,收益为并加总得到决策理论中称为“完全理想收益”。通常将rijpj之间的差额描述为信息价值,可以通过后验信息来缩小这个差额,如果经过后验修正后差额减小,表明信息有效,反之无效,这点在后面具体分析。笔者在这里提出一个新的bayes结果处理方案:
假设在先验信息条件下,确定最优营销方案为ai,则在不同状态概率条件下的收益集为RP1={ri1p1,ri2p2,…,rinpn},但理想状态下,各状态概率下采取的决策方案为A={ak1,ak2,…,akn},相应的收益集为RP2={r11p1,rK22p2,…,rknnpn},则在状态θj时,由新情报引起的价值上升为△j=rkijpj-rijpj,表示在状态θj下,因为情报成熟度差异导致的亏损收益。这样对状态θ中的n个状态的情报成熟影响度进行排序,最大的△j刻度了maxθj是最容易受到情报因素影响的,最小的minθj不容易受到情报影响,基本可以按照原始bayes决策体系进行预测。那么针对较大的θj下△j的如何修正呢?笔者通过引入后验信息进行修正,来度量信息价值。
1.2 后验信息的引入
导致我国保险市场落后于其经济社会整体发展水平的原因是多样的,其中首要原因是我国大多数人保险意识比较淡薄,对保险知识了解较少,还没有充分认识到保险是转嫁农业经营风险、保护自身利益的有效途径[2]。那么在这样的市场背景下,一个保险产品无论设计的如何好,计划制定的如何完美,都可能最终失败。试验——不仅仅能够使保险机构能够摸清市场状况,更有助于试验对象对即将推行的产品有更深的了解,形成深刻的影响,从而达到“一传十、十传百”的扩散效应。
假设保险机构预测到未来有n种市场状态及相应概率,但由于保险市场不同于其他有形产品市场,任何预测结果都不如有形产品得到的状态概率稳定。必须引入后验信息,引入方式为调查问卷。建议分两轮调查:第一轮请参保客户对某险种的未来购买意愿进行阐述,得到各种状态概率θj,第二轮为隔断时间再对相同对象进行调查,这样便得到原来选择状态θj的客户现在的倾向分布Dij(满足)。得到联合概率分布:PDij=PiDj。
得到联合概率分布:PDij=PiDij,根据公式P(A)=P(B)P(A/B)可求出边缘概率:
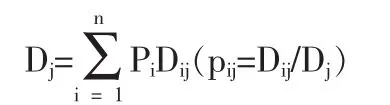
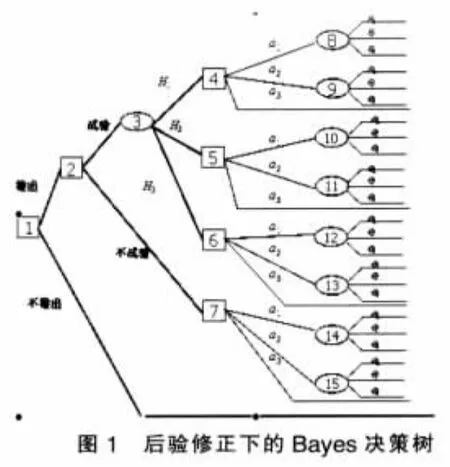
同样,根据公式P(A)=P(B)P(A/B)求出后验修正概率P修=这里用三种预测状态和三种试验结果为例,做出后验信息下的Bayes决策树(见图1)。
重新定义原始状态概率X={x1,x2,…,xn},修正后状态概率为,状态概率修正幅度为Y=(y1,y2,…,yn),因为完全信息(后验)带来的收益修正幅度为可以推断因为在实际中完全信息不可得,那么可得
概率学习即在确定网络结构的前提下,结合样本数据集,确定根节点的先验概率和中间节点的条件概率分布的过程。在得到更多的数据时,贝叶斯网络可以利用这些新数据对网络结构和参数进行更新,也是从先验联合分布到后验联合分布的过程[3][4]。笔者对后验修正中的概率状态进行修正分解,得到每一个概率状态下的修正幅度,这样有利于决策者在对未来一段时间内市场状态有个客观认识后进行定量与定性相结合的评价,比如某保险产品在未来一段时间按照各种现实情况评价得出绝大部分可能是属于滞销状态,那么采取传统贝叶斯决策就无法准确客观进行决策,但又不能脱离已有体系框架,这样分离Bayes后验体系就发挥了很大作用。具体将通过一个算例进行解释。
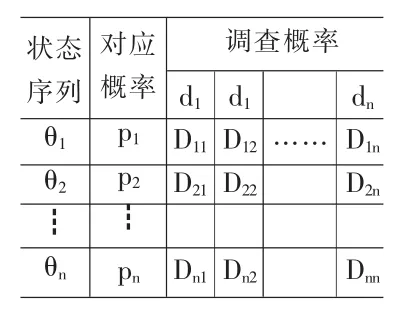
表2 后验修正下的概率分布
2 算例运算
2.1 后验运算
某保险公司根据2009年的财产保险市场总结及行情分析,结合本公司及所在地域实际,进行保险营销决策。保险营销决策是理性行为的基础,有明确的目的,有两个以上的可行方案,要进行因果分析和综合评价,要经过方案的优选过程。假设方案集为η={直销,中间人,网络营销}。为了方便叙述,记为:η={η1,η2,η3}。直销为保险公司直接向客户推销保险,有利于控制风险,稳定业务量。但随着业务规模的不断扩大,人力资本和市场资源的不足要求中间代理人形式的间接营销方式出现,以致到21世纪网络发达时代,网络这一大范围、低成本的保险营销方式为人所青睐。
同样市场也有相应的状态集θ,刻度了产品市场即将可能面临的环境。记为θ={θ1,θ2,θ3}。其准确度(似然分布矩阵)由表3表示。
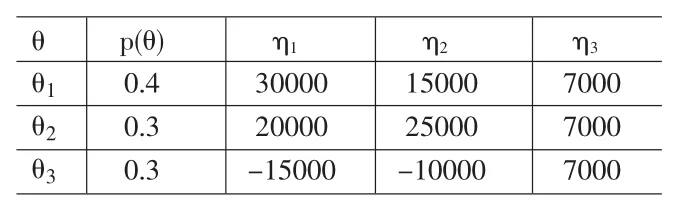
表3 某保险公司销售财产险的收益似然分布矩阵
保险公司为了充分了解2010年的相关产品市场情况,在正式推出前对一部分客户进行意向调查试验,由于试验工作需要人力及物力成本,需要相关费用800元,得到三种试验结果,分别为受欢迎(H1)、一般(H2)、较差(H3)。这样便得到相关似然矩阵(见表4)。
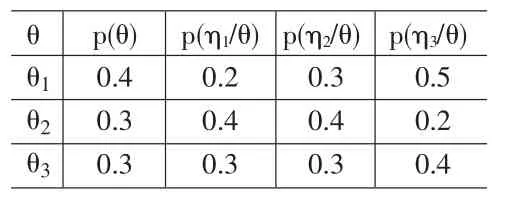
表4 后验信息下的概率分布似然矩阵
因为保险公司每年的工作重点可不尽相同,如果财产险市场前景不良,则可以将相应的投入放在其他项目上,这样会引起机会收益。假设将同样费用放在其他项目上引起收益5000元。这样,会引起三个决策问题,具体如下:
(1)是否实行财产险种?
(2)如果实行,是否采取试验办法?
(3)如果不试验,应直销,代理销售还是网络销售?如果试验,应该如何实行销售?
首先根据
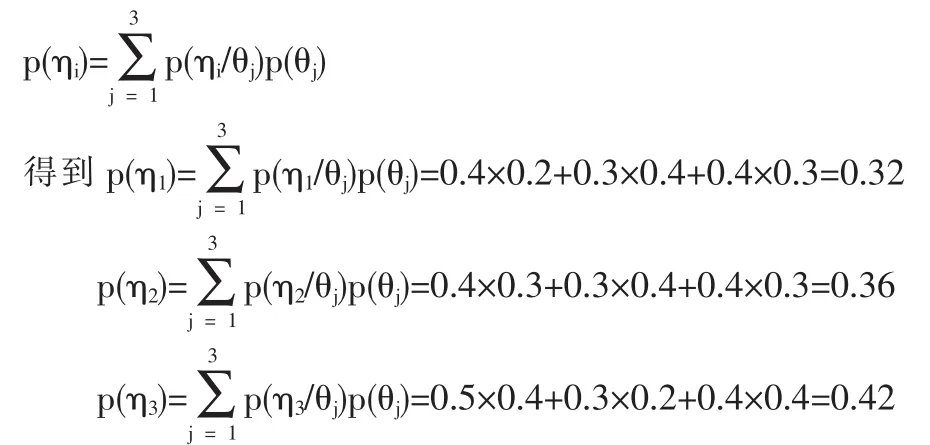
根据p(θj/ηi)=p(ηi/θj)p(θj)/p(ηi)
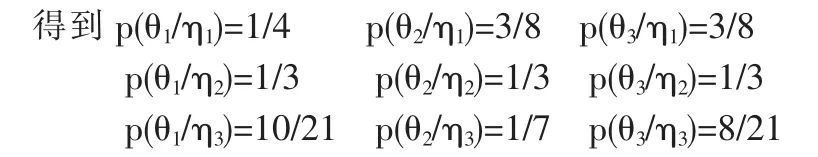
故试验结果为η1时,收益期望为
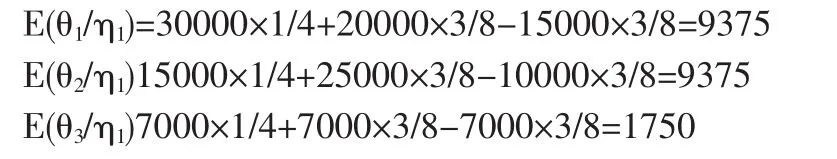
当试验结果为η1时,采取直销和代理销售均可。
E(θ1/η2)=30000×1/3+20000×1/3-15000×1/3=11333
E(θ2/η2)=15000×1/3+25000×1/3-10000×1/3=10000
E(θ3/η2)=7000×1/3+7000×1/3-7000×1/3=2333
当试验结果为时,采取直销方式。
E(θ1/η3)=30000×10/21+20000×1/7-15000×8/21=11418
E(θ2/η3)=15000×10/21+25000×1/7-10000×8/21=6903
E(θ3/η3)=7000×10/21+7000×1/7-7000×8/21=1667
当试验结果为η3时,采取直销方式。
故经过概率修正后,在各种试验结果下,直销方式为最佳销售方式。这里算出试验收益:
E(θ1/η3)p(η1)+E(θ1/η2)p(η2)+E(θ1/η3)p(η3) =9375×0.32+11333×0.36+11418×0.42=11875
减去800试验费用,纯收益为11075元。
如果不试验,则:
采取η1决策可得到期望收益:30000×0.4+20000×0.3-15000×0.4=12000
采取η2决策可得到期望收益:15000×0.4+25000×0.3-10000×0.4=9500
采取η3决策可得到期望收益:7000×0.4+7000×0.3-7000×0.4=2100
2.2 后验修正有效性分析
上节证明选择直销方式为最优方式。并且收益明显高于运行其他保险项目的收益(5000),故不试验下的直销方式为最优解。依据上述计算结果构建bayes评价体系表(见表5)。
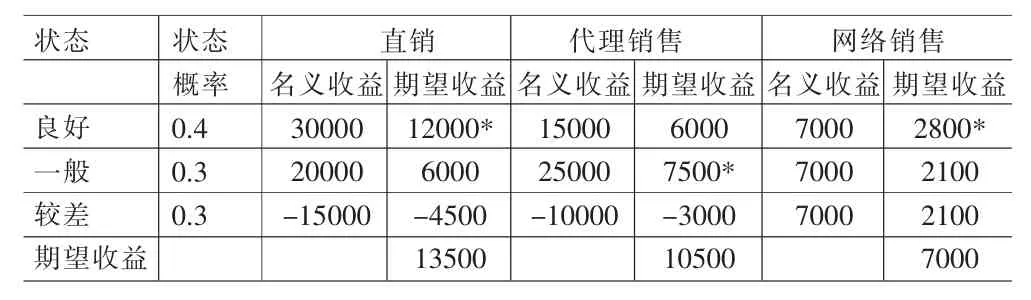
表5 bayes评价体系表
最佳决策为直销,期望最大收益为13500,但完全期望收益为=12000+7500+2800=22300元。完全信息价值=22300-13500=8800元。故=8800/ 13500=65.18%,其中=[0,11.11%,54.07%],表明某保险公司在进行营销决策时太过于偏好认为较好情况的发生,但对较差状态可能性考虑不足,如果将来发生由于较差状态带来的损失,将会出现重大决策失误。[21.74%,54.78%,23.48%],可以发现本次修正概率变动趋势与由Bayes矩阵估计出的概率变动趋势不一致,表明本次后验概率修正无价值,应重新进行修正。假设修正概率后的变动趋势b2,b3](b1+b2+b3=1)笔者给出后验有效性判定法则:
(1)[a1,a2,a3]与[b1,b2,b3]集合中三元素排序一致时,如出现任一顺序不一致,试验结果无效。
(2)序列a1、a2、a3和[b1,b2,b3]的方差σ1和σ2,经过均值误差检验:在一定显著性条件α下小于Fα(n-1),即两者均值误差显著服从于0。若显著不为0,则试验得到后验效率无效。
3 结论
在许多实际问题中,通过试验获取的信息可更为精确地判断事件发生的可能性大小,从而可以采取更有利的行动来增加收益或减少损失,但进行试验是需要经费的支出的,因此还应考虑经济上的合理性[5]。但是并不是任何信息都是有价值的,在信息爆炸时代,对信息进行搜集、甄别、确定利用或部分利用的过程非常关键,但在目前决策理论与方法运用过程中,往往默认后验信息是绝对有利的,这是一个非常错误的潜规则。基于此,笔者具体到保险产品营销决策,提出信息有效判定准则和后验概率修正价值公式。保险业作为几十年来我国金融资本市场的兴起行业,在维持社会稳定和活跃金融环境上有重大的双重作用,但由于保险产品与传统有形产品存在很大差异,其市场特性和发展趋势有特殊性,在市场营销中面临着很大的不确定性,在很大程度上并不依赖前期市场情况,所以国内相关学者采用markov等无追溯性的预测和评价公式对包括保险行业在内的资本性行业进行预测评价,是相当不科学的。犹如DEA法不仅能对经济社会系统进行评价,还能分析出投入或产出的不足与过剩,也应当有一种方法能实现决策中后验情报信息的判定和测度。根据本文的研究结论,保险市场营销中后验情报具有很大的不准确性,能够很好地作为一个验证新情报信息失效的分析产业,在庞大的国民经济系统中,必然存在着类似于保险业这样的众多行业存在信息失真现象,那么这种判定就显得尤为重要。希望本文能够改变以往决策理论中对后验情报完全信任的一边倒现象,有辩证的思维和眼光看待情报信息,以便取舍和选用;同时一些即时有情报的信息所带来的价值也不一定能和机会投入相媲美,这涉及到多阶段和多目标等决策内容,希望有关学者能进一步对此问题有更深刻的研究。
[1]李兵.我国保险营销创新的可行性选择[J].企业经济,2006,(8).
[2]吴思,王长征.农村保险市场营销模式创新——基于水平营销的视角[J].保险研究,2010,(4).
[3]慕春棣,戴剑彬,叶俊.用于数据挖掘的贝叶斯网络[J].软件学报, 2000,(5).
[4]李军,陈士俊.张云起.基于贝叶斯网络的营销风险评价研究[J].西北农林科技大学学报(社会科学版),2007,(3).
[5]吴志远,张振强.由先脸概率和后验概率谈信息的价值[J].南宁师范高等专科学校学报,2004,(3).
[6]方志耕等.决策理论与方法[M].北京:科学出版社,2009.
(责任编辑/亦民)
O211.9
A
1002-6487(2011)05-0014-03
聂尔德(1964-),男,安徽合肥人,讲师,研究方向:保险、国际金融。

