基于信息差异化的双寡头企业选址定价博弈

朱启红，顾锋

（1.上海立信会计学院工商管理学院，上海201620；2.上海交通大学安泰经济与管理学院，上海200052）

基于信息差异化的双寡头企业选址定价博弈

朱启红1，顾锋2

（1.上海立信会计学院工商管理学院，上海201620；2.上海交通大学安泰经济与管理学院，上海200052）

文章建立了一个三阶段博弈模型，研究两个寡头垄断企业在信息性广告竞争中定价、定址决策问题。结果表明，企业在信息和地址两个维度下，对称均衡是两个企业位于线性城市的两个极端，实现最大差异化，以尽量缓和价格竞争；在企业广告成本固定的情况下，双寡头企业选址定价博弈均衡同样显示出最大差异化。

信息差异化；双寡头企业；广告水平；定价定址博弈

0 引言

在产品差异化理论中，产品的差异通常被划分为纵向差异、横向差异和信息性差异（泰勒尔，1997）[1]。其中产品质量特性方面的差异，称为纵向（垂直）差异；其他产品特性的差异为横向（水平）差异；信息差异是指产品在信息传播上的差异，其本质是同类乃至同质的产品经过广告的着意渲染而使消费者对产品产生主观认知的差异（顾锋，2007）[2]。

根据产品差异的不同类型，经济理论中研究产品差异化竞争的模型主要有三大类：一类是水平或横向差异模型，其中Hotelling提出的线段模型[3]和Salop提出的圆形市场模型[4]就是研究产品水平差异竞争的有效方法；一类是垂直或纵向差异模型，围绕Dixit等[5]以及Spence[6]提出的纵向差异化与质量竞争模型为经典模型展开；在信息性差异模型研究方面，主要有Butters（1977）模型[7]和Grossman和Shapiro（1984）模型[8]。在泰勒尔（1997）构建信息性广告竞争模型中，事先假定两家企业分为位于长度为1的线性城市两个极端，两家企业同时选定价格和广告水平，探讨均衡时广告对需求和产品差异化的影响[1]。

本文构建一个三阶段博弈模型，研究双寡头垄断企业在信息性广告竞争中的定价、定址决策问题。

1 模型建立

1.1 模型的若干假定

考虑一个长度为1的线性城市，市场上两家企业产品的差异化系数d1和d2代表产品的“位值”，分别用a和1-b(b> 0)表示，不失一般性1-a-b≥0（企业1在企业2的左边，a=b= 0与最大差异化相对应，a+b=1与最小差异化相对应）。两家企业销售品牌不同但事实上是同质的产品，单位成本为c。消费者以1的密度均匀地分布于这个线段，单位距离的运输成本是t；消费者有单位需求，即他们消费0个或1个单位的该种商品，他们通过消费者这一商品得到总盈余为s，如果以价格p去购买，则消费者所获效用为U=s-p；如果不购买，则效用为0。

假设消费者获得一个产品存在和价格的信息的唯一途径是企业随机发送的广告，消费者无法搜寻有关产品存在和价格的信息。也就是说，当且仅当消费者从一个对应企业接到一个广告的话，他才能消费一个产品。以准i(i=1，2)代表从企业i接到一份广告的消费者的比例。进一步，假设广告不是地方化的，住在沿这一线段的消费者都有同等的机会得到一份给定的广告，企业的广告水平和定价无关。设A(准i)为使准i比例的消费者接到企业的广告，企业i所支付的成本，由于广告是随机发送的，所以准i也是一个消费者至少接到企业i的一份广告的概率。这里A'>0，A''>0，为简化计算，我们采用泰勒尔（1997）的广告成本函数A(准；λ)=λ准2/2，λ>0为常数。

1.2 需求分析

由于假定消费者获得产品有关信息的唯一途径就是广告，消费者不会主动去搜寻信息，也就是说，只有在接到企业的广告后才知道产品的存在且在接到广告后一定会购买产品。根据所接到的广告，可将消费者分为四类：第一类消费者只接到企业的广告，其比例为准1(1-准2)；第二类为只接到企业广告的消费者，其比例为准2(1-准1)；第三类消费者同时接到企业和广告，其比例为准1准2；第四类消费者没有接到一个企业的广告，其比例为(1-准1)(1-准2)。

其中准1(1-准2)+准2(1-准)+准1准2+(1-准1)(1-准2)=1因此，企业1的潜在需求规模由两部分组成：

第一部分为只拥有企业产品信息的消费者，即收到企业的广告，而没有接到企业的广告的消费者，这部分需求构成企业的领地，沿这一市场线段的每个消费者都愿意购买企业的产品，其规模为：

第二部分为拥有产品的全部信息且选择购买企业产品，即同时接到企业和企业的广告的消费者中准1准2，愿意购买企业1的产品。由于同时接到两个企业的广告的消费者构成一个具有竞争性的需求部分，两企业需要为这部分“共同的需求”而竞争。因此，消费者此时需要比较购买企业的产品的所获得净效用和购买企业产品所获得的净效用的大小来决定。在“共同的需求”部分，假设两企业分别选择了价格p1和p2。如果两家企业之间的价格差不超过穿过整个城市的运输成本，且如果价格不太高使得所有消费者从所有企业消费的效用均不大于零，则就会有一个位于x的消费者，实际效用分别为：

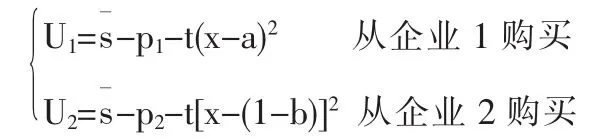
若消费者从两家企业购买产品所获得的实际效用无差异(U1=U2)，即：

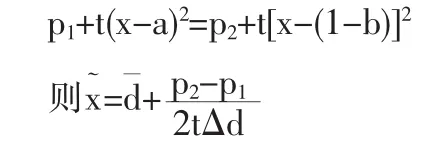
第二部分的需求规模是：

由（1）和（2）式相加得到企业1的需求规模为：

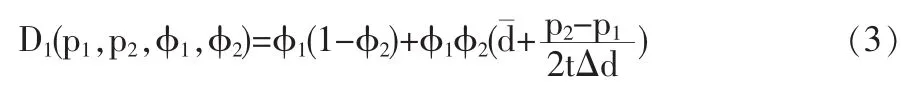
同理，可知企业2的市场需求规模为：

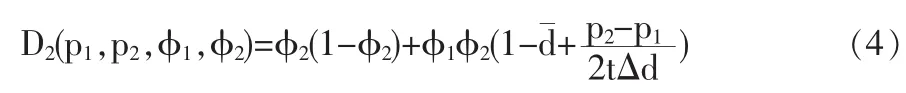
从而，两个企业的利润分别为：

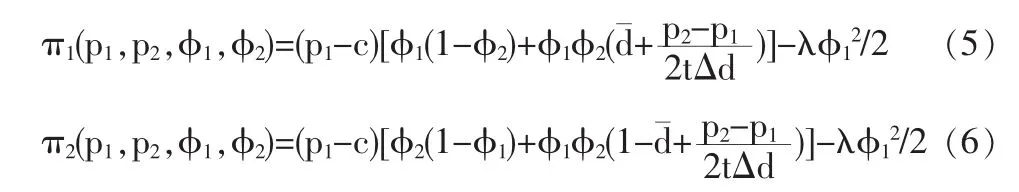
2 均衡讨论

考虑这样一个三阶段博弈：第一阶段，企业同时选择地址，即企业同时决定产品的市场定位策略；第二阶段，在地址给定的情况下，两家企业同时为其差异化产品选择广告水平；第三阶段两家企业同时选择产品的定价策略。用逆向归纳法，先找出第三阶段价格竞争的均衡解，再推导第二阶段的企业广告水平竞争的均衡解，最后推导出第一阶段的企业产品差异化定位策略解。

2.1 博弈的第三阶段：最优定价策略

首先分析最后阶段的博弈，同时给定两企业地址和广告水平的情况下，第三阶段博弈的价格竞争意味两企业分别选定价格pi以最大化利润πi，由价格竞争Nash均衡的一阶条件：

联立（7）和（8）求解，可得出均衡时两企业的价格水平：

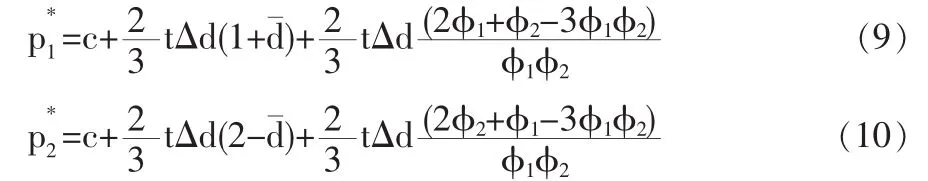
将（9），（10）分别代入（5）和（6），可求出第三阶段两企业利润分别为：

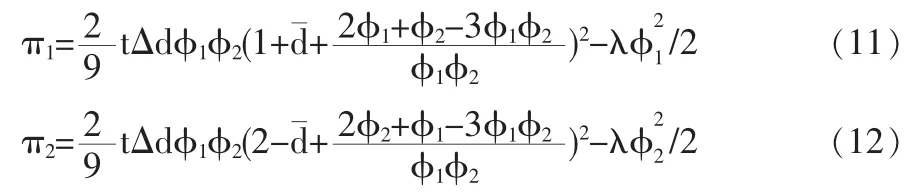
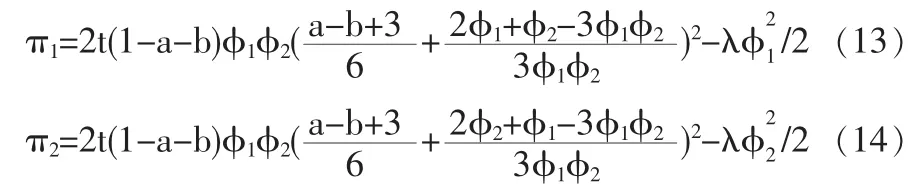
2.2 博弈的第二阶段：最优广告水平策略

接下来分析博弈的第二阶段，给定企业的地址，两企业选择广告水平准i以最大化利润πi，由价格竞争Nash均衡的一阶条件：

当a=b且t>2λ的情况下，我们可求准1=准2=准*的对称均衡。

解方程式（15）和（16）可得：

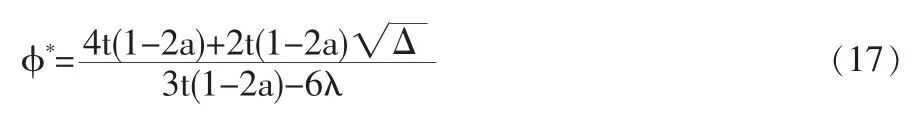
把（17）代入企业1的利润函数：

2.3 博弈第一阶段：最优选址策略

企业在第一阶段的最优选址a*、b*分别满足a*∈arg max和由利润对位值的一阶导数可得：

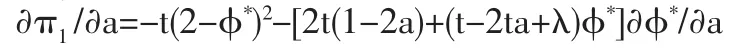
由于1-2a>0，t>2λ，t-2ta+λ>0；鄣准*/鄣a>0

因此鄣准*/鄣a<0

3 广告成本的讨论

在上面讨论的模型中，企业广告支出的多少决定了广告水平的大小，即提供信息量的大小。当企业广告成本为固定值K，即与广告水平准无关时，我们需重新讨论模型的均衡。由上文的讨论可知，企业的需求规模没有发生变化，利润函数分别为：

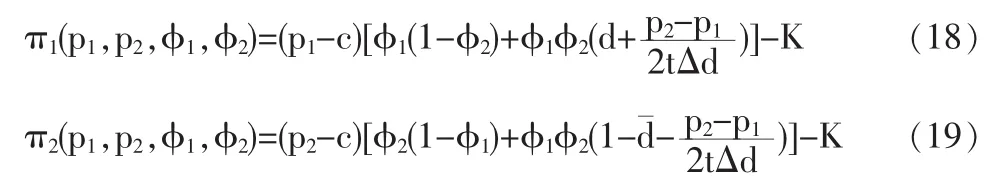
同样运用逆推归纳法讨论模型的均衡。首先分析最后阶段的博弈，同时给定两企业地址和广告水平的情况下，第三阶段博弈的价格竞争意味两企业分别选定价格pi以最大化利润πi，由价格竞争Nash均衡的一阶条件：

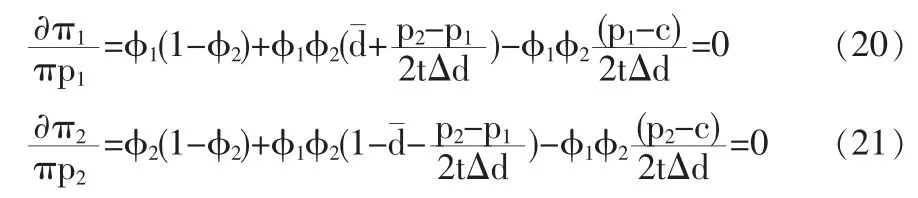
易验证二阶条件满足。

联立（20）和（21）求解可得出均衡时两企业的价格水平：

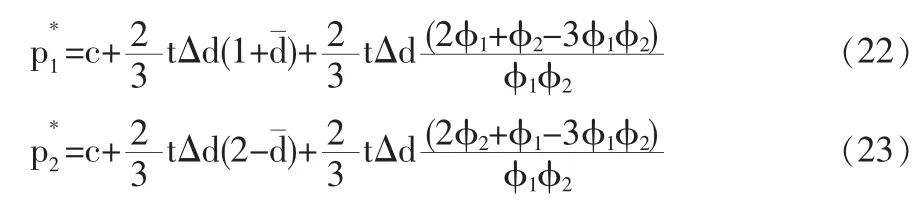
将（22）和（23）两式分别代入（18）和（19），可求出第三阶段两企业利润分别为：

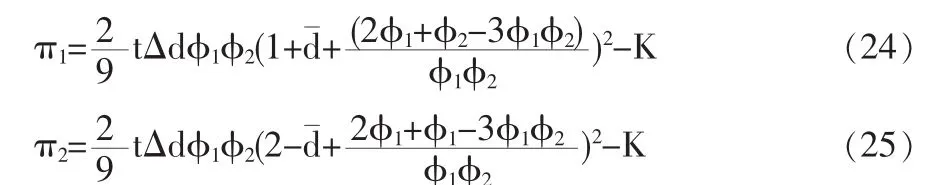
接下来分析博弈的第二阶段，给定企业的地址，两企业选择广告水平准i以最大化利润πi，由价格竞争Nash均衡的一阶条件：

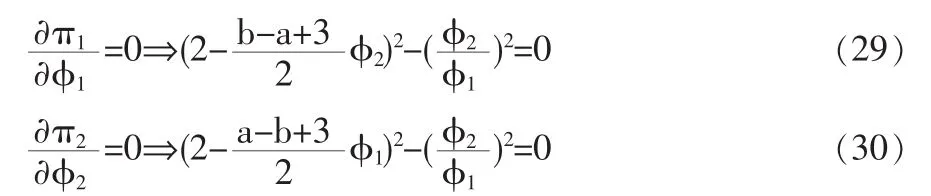
联立（29）和（30），求解方程组可得第二阶段企业的均衡广告水平：

将（31）和（32）两式分别代入（24）和（25），可求出第二阶段两企业利润分别为：和

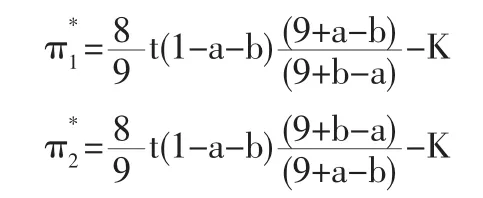
回到博弈的第一阶段，企业在第一阶段的最优选址a*、b*分别满足由利润对位值的一阶导数可得：由于1-a-b≥0，因此

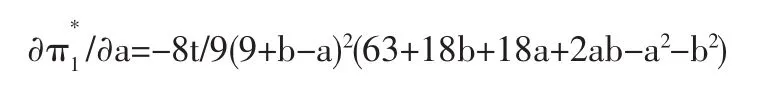
4 结语

通过广告来制造的信息性产品差异，可以降低产品研发和生产的投资，提高产品差异制造过程的灵活性和可操作性，因而成为非常流行的营销手段。在三阶段的信息性广告竞争模型中，运用倒退归纳法得出两个企业的市场需求函数以及利润函数，并由此给出企业在信息和地址两个维度下，对称均衡是两个企业位于线性城市的两个极端，实现最大差异化，以缓和价格竞争。本文还对企业广告成本进行了讨论，结果表明在企业广告成本固定情况下，企业选址的纳什均衡同样显示出最大的差异化。本文模型假定广告是消费者获得产品信息的唯一途径，事实上，消费者除了被动接受企业广告信息外，还可以主动进行搜寻，存在信息搜寻的差异化模型将是进一步研究的方向。

[1]泰勒尔.产业组织理论[M].张维迎译.北京:中国人民大学出版社, 1997.

[2]顾锋.黄培清.基于品牌忠诚的企业多阶段竞争策略研究[J].系统管理学报,2008,(6).

[3]Hotelling,Harold H.Stability in Competition[J].Journal of Economic, 1929，(39).

[4]Salop,S.Strategic Entry Deterrence[J].American Economic Review, 1979,(69).

[5]Dixit,A.K.,Stiglitz,J.E.Monopolistic Competition&Optimum Product Diversity[J].American Economic Review,1977,67(3).

[6]Spence,M.ProductSelection.FixedCostsandMonopolistic Competition[J].Review of Economic Studies,1976,(42).

[7]Butters,G.Equilibrium Distribution of Prices and Advertising[J]. Review of Economic Studies,1977,(44).

[8]Grossman,G.,Shapiro,C.Informative Advertising with Differentiated Products[J].Review of Economic Studies,1984,(51).

[9]C.D’Aspremont,J.J.Gabszewicz,J.F.On Hotelling’s Stability in Competition[J].Econometrica,1979，(47).

（责任编辑/易永生）

F273

A

1002-6487（2011）05-0072-03

国家自然科学基金资助项目（70572102）

朱启红（1977-），女，博士，讲师，研究方向：企业管理和博弈论。

顾锋（1963-），男，教授，博士生导师，研究方向：博弈论和企业管理。