基于ARIMA-GMDH的GDP预测模型

尹静，何跃

（四川大学工商管理学院，成都610064）

基于ARIMA-GMDH的GDP预测模型

尹静，何跃

（四川大学工商管理学院，成都610064）

文章先对四川省GDP分别建立了ARIMA时间序列模型和GMDH变量自回归模型来进行预测；然后利用GMDH自组织建模方法建立ARIMA-GMDH组合预测模型来预测；最后使用Bonferroni-Dunn方法对三个模型的稳定性进行分析检验。模型预测结果和稳定性检验结果表明：基于ARIMA-GMDH组合的GDP预测模型的拟合和预测都优于另外两种单预测模型。相比之下组合模型在拟合和预测效果具有较高的可靠性、准确性和稳定性。

GDP；ARIMA；GMDH；组合预测

0 引言

对GDP的定量预测模型种类繁多。最初人们多用单一模型预测，如回归分析法、时间序列分析法、灰色预测法、人工神经网络法等。但是不同的预测方法也自身存在局限性，可能会影响预测效果。例如ARIMA模型可能存在共线性、过拟合的现象，会影响模型的预测能力[1]；GMDH自回归模型的不同数据分组预测出来的结果不同，导致预测结果有偏差[2]；而组合预测能克服单个模型预测的局限性，能够综合各种模型的有用信息，最大效用地利用各个模型的有用信息，减少单个模型受随机因素的影响，使预测的精度得到提高。根据参考文献[2]，自组织组合预测模型要优于最优组合模型和人工神经网络组合预测模型，因此采用此方法组合预测。

本文尝试首先分别利用ARIMA、GMDH自回归模型对四川省季度GDP进行预测，在此基础上建立基于GMDH的两种模型的组合模型；最后使用Bonferroni-Dunn方法做模型稳定性检验。

1 预测模型简介

1.1 ARIMA模型介绍

ARIMA(p，d，q)自回归求积移动平均(Auto Regressive Integrated Moving Average)模型由美国统计学家G.E.P.Box和G.M.Jenkins于1970年首次提出，广泛应用于各种类型时间序列数据的分析方法，是一种预测精度较高的短期预测方法。其实质是差分运算与ARMA模型的组合。此模型是从数据本身出发来寻找可以较好描述数据的模式，从而可以保证模型与数据的拟合较好，但是也存在共线性和过拟合现象，影响预测效果。

ARIMA模型拟合和预测的基本步骤：

（1）数据进行平稳化处理与检验。ARIMA模型建模方法是以序列平稳性为前提。检验的标准方法是单位根检验，若序列不满足平稳性条件，则可通过数学方法，如差分变换或者对数差分变换使其满足平稳性条件。

（2）模型识别。通过计算能够描述序列特征的一些统计量，如自相关(ACP)系数和偏自相关(PACP)系数来确定ARMA(p,d,q)模型的阶数p和q，并根据一定的准则，如AIC准则或SC准则等综合考虑来确定模型的参数，使参数尽可能少。

（3）估计模型的未知参数，并通过参数的T统计量检验其显著性，以及模型的合理性。

（4）进行诊断分析，检验模型的拟合值和实际值的残差序列是否为一个白噪声序列，证实所得模型确实与所观察到的数据特征相符。

1.2 GMDH自回归模型介绍

数据分组处理方法（Group Method of Data Handling，GMDH）是由乌克兰科学院A.G.Ivakhnenko院士于1967年首次提出的，并由德国学者J.A.Mueller和软件专家L.Frank在软件KnowledgeMiner中具体实现了目前他们提出的算法，使其不断应用发展。

GMDH算法是建立在“进化－遗传－变异－选择”的进化论原理基础上的，重复这样一个遗传、变异、选择和进化的过程，使中间待选模型的复杂度不断增加，直至得到最优复杂度模型[2]。

自组织建模算法的主要步骤：

①将观测样本数据分成训练集和检测集；

②在每阶段按不同的变量和增长的复杂度产生待选模型；

③对于参数模型，在训练集上估计未知参数；

④在每阶段利用检测集的数据选出一些最好的模型；

因此自组织区别于一般回归模型的最大的优点是它将数据分为训练集和测试集，在训练集上使用内准则进行参数估计得到中间待选模型，而在测试集上使用外准则进行中间候选模型的选择，这个过程不断重复直到外准则值不能再改善才停止，这样的停止法则可以保证在一定噪声水平下得到数据拟合精度和预测能力之间实现最优平衡的最优复杂度模型，不会出现一般的回归方法中常出现的过拟合而牺牲了预测能力的现象。

而GMDH自回归模型是将自组织数据挖掘中的GMDH算法与传统自回归模型相结合而产生的一种预测方法。与传统的自回归分析方法相比，GMDH自回归模型在小样本区间上能较好地进行系统的拟合预测工作[3]。

1.3 组合预测模型

组合预测，就是将不同的预测方法进行适当的组合，综合利用各种方法所提供的有用信息，从而尽可能的提高预测能力。目前已知的组合预测方法主要有权系数组合预测法、非线性组合预测法和自组织组合预测方法[2]。

但是权系数组合预测法的特点是认为参加组合预测的各个预测模型间是一种线性关系，而往往单个预测模型都是非线性的；非线性组合预测法所需设计的参数比大多数统计预测模型都多，有时会造成网络模型的过拟合现象，即这种模型虽然对样本数据有较高的拟合精度，但预测能力差。自GMDH组合预测模型恰好能解决这些问题，因此，选择基于GMDH的ARIMA-GMDH组合预测模型。

2 实证分析

由《四川省统计年鉴》得到2000年1季度到2009年4季度共40个四川省GDP季度累计值作为组合预测模型的原始数据。但由于通货膨胀等因素可能造成各年的价格有差异，全部按照2000年价格作可比价处理数据。将其中2000年1季度到2008年4季度共36个数据用于预测模型，2009年1季度到2009年4季度共4个数据作预测检验数据。

2.1 ARIMA时间序列模型预测

ARIMA时间序列模型预测法计算过程非常复杂，用EVIEWS软件[6]对四川省GDP数据进行一系列处理和分析。

2.1.1 数据预处理

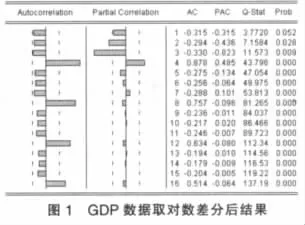
首先对数据平稳性进行检验，从GDP数据的序列图可以看出GDP数据不具有明显的周期变化和季节波动，是非平稳的，且呈现出指数发展趋势，可以通过取对数将指数趋势转化为线性趋势，然后再对GDP数据取对数后进行一阶差分。差分后如图1所示，可知自相关系数与偏相关系数落入置信区间并快速趋近于零，数据变得平稳。

2.2.2 模型识别

ARIMA(p,d,q)模型中d已经确定为1，现需要确定p与q的值。我们引人自相关系数和偏自相关系数这两个统计量来识别ARMA(p,q)模型的系数特点和模型的阶数。由图1可知，自相关系数与偏相关系数都具有拖尾性，自相关系数在k=3和4时显著不为0，所以确定p的值为2,，3或4。偏相关系数在k=2，3和4时显著不为0，则确定q的值为3或4。那么可能合适的（p，q）组合为（3,2），（3,3）（3,4），（4,2），（4,3），（4,4）。

2.2.3 模型建立

经过多次尝试和检验后，模型检验结果如表1所示，根据AIC值越大越好，SC和Adjusted R-squared值越小越好的原则，确定最终模型为ARIMA(4,1,4)。

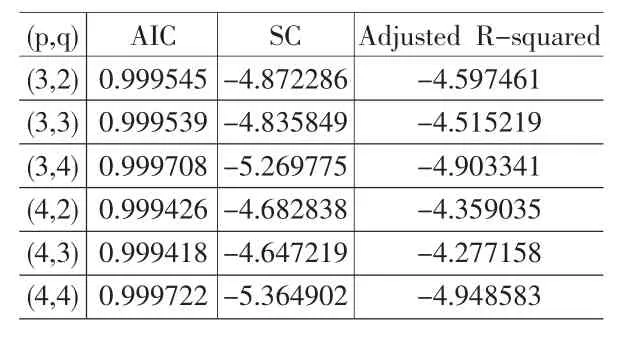
表1 ARIMA模型检验结果

2.2.4 预测模型

在模型ARIMA(4，1，4）的基础上消除多重共线性得到最佳拟合模型如下：

其中Z为X的一阶差分，即Z=△X，X=1n(GDP)，GDP为2000年1季度到2008年4季度可比价。

最终预测模型为：

2.2 GMDH自回归模型预测

根据GMDH预测模型原理，利用软件Knowledge Miner计算过程如下：

（1）首先输入数据，选择预测GMDH自回归预测模型，确定模型，其中最重要的参数有max.time lag和Model Type。根据经验我们得知第一个参数跟输入数据的类型有关，如数据是月度数据一般为12；为季度数据时，一般为4。

（2）确定参数后，我们应该根据外准则原则：选取Coefficient Of Determination（R-squared）和adjusted R-squared达到最低点又再回升时，预测效果为最好。对于四川季度GDP累计值，当max.time lag取4，Model Type取exclusively linear时，此时Coefficient Of Determination(R-squared)和adjusted R-squared值最佳。

（3）最优预测模型

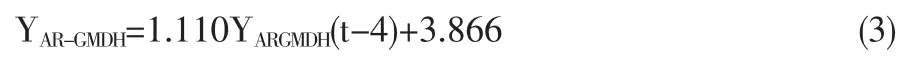
2.3 基于GMDH的组合预测结果

GMDH方法采用多层迭代的方法，利用Knowledge Miner软件选取组合预测模型来做组合预测。建立模型确定参数时，同样根据外准则原则选取最佳参数预测最优结果。

以YARIMA，YAR-GMDH作为模型的输入，使用GMDH方法将各个单项预测模型的结果组合起来，最终自组织建模软件（Knowledge Miner）筛选出最优复杂度模型为：

2.4 预测结果分析比较

经过2008年的金融危机和四川地震灾害，导致自2008年4季度以来至2009年1季度四川省GDP明显回落，宏观经济进入本轮经济周期的下行区间；但是经过国家的投资拉动和灾后重建，2009年2、3、4季度已开始回升。三种模型对于四川省GDP的预测误差都在3%以下，在可接受范围内，具体预测结果如表2。

表2 2009年1～4季度单项预测模型与组合预测模型GDP预测结果

从表2看，ARIMA模型的标准误差为2.30%，GMDH自回归模型的标准误差为2.43%，组合预测模型预测的标准误差仅为1.67%，并且组合预测模型的相对误差与单项模型相比都有所改善，得到的预测效果较为可靠和满意，说明通过GMDH组合后的预测模型能在很大程度上减少由单个模型带来的误差，具有一定的抗干扰性，从而保证预测的准确性。

3 模型拟合能力分析

为了进一步分析各个模型的稳定性，使用Bonferroni-Dunn检验方法来验证单项模型与组合模型之间在模型拟合方面是否存在显著的差异。

Bonferroni-Dunn检验方法是将模型拟合值与实际值进行比较，并按照差值的绝对值从小到大进行排序，若差值相同，则赋一个平均排序，最后计算每一种模型所有时间内的平均排序。根据Bonferroni-Dunn检验，若每两种模型之间拟合的差异是显著不同的，那么它们之间平均排序的差值应该至少要大于下面的临界值：

其中qα为在相应显著性水平下的Bonferroni-Dunn检验临界值，k为模型的个数，N为拟合数据的条数。

2002年1季度至2008年4季度各预测模型数据拟合值与排序结果如表3所示。

表3 2002年1季度-2008年4季度各预测模型数据拟合值与排序结果

在α=0.05时，qα=2.241，计算得CD值为0.5989，由此可知，在置信度为95%的水平下，组合预测模型的数据拟合能力要优于ARIMA模型（2.2857-1.5357>0.5989）与ARGMDH模型（2.1786-1.5357>0.5989）。

4 结语

本文通过对四川省2000年1季度到2009年4季度的GDP累计值数据（按2000年可比价格）进行预测检验，分析得到：ARIMA模型和GMDH自回归模型模型比较适合预测宏观经济指标，组合预测模型的预测结果更优于单一模型预测结果,因此组合预测模型的应用更具有实际意义。

但是为了达到更好的预测效果，我们应该不断地提高和改进各单项模型和组合模型的拟合与预测能力，同时可以寻找更好的组合模型进行预测。根据稳定性和拟合效果的分析，拟合效果好的预测结果不一定是最优的。这给我们的启示是：每种预测模型都有其自身的优点、缺点和适用范围，我们应该根据具体情况选择最优预测模型。

[1]何跃，鲍爱根，贺昌政．自组织建模方法和GDP增长模型研究[J]．中国管理科学，2007，(2)．

[2]贺昌政.自组织数据挖掘与经济预测[M].北京：科学出版社，2005.

[3]贺昌政，俞海，卢跃奇．自组织组合预测方法及其应用[J]．数量经济技术经济研究，2002，(2)．

[4]王莎莎，陈安，苏静，李硕．组合预测模型在中国GDP预测中的应用[J]．山东大学学报，2009，(2)．

[5]赵蕾，陈美英.ARIMA模型在福建省GDP预测中的应用[J]．科技和产业，2007.

[6]易丹辉．数据分析与EVIEWS应用[M]．北京：中国统计出版社，2002.

[7]曹玉洁，何跃，贺昌政．基于R/S分析的GMDH自组织方法在用电量预测中的应用[J]．软科学，2009，(7).

（责任编辑/亦民）

F201

A

1002－6487（2011）05－0035-03

国家自然科学基金资助项目（70771067）

尹静（1986-），女，河北保定人，硕士研究生，研究方向：信息管理与信息系统。

何跃（1961-），男，重庆人，博士，副教授，研究方向：管理信息系统、数据挖掘、决策支持系统。