两种数据校正模型性能的统计特征分析与比较

延树港，周溪召，高林，陈晶

（1.上海海事大学a.物流工程学院；b.商船学院，上海201306；2.华东理工大学信息学院，上海200237）

两种数据校正模型性能的统计特征分析与比较

延树港1a，周溪召1a，高林2，陈晶1b

（1.上海海事大学a.物流工程学院；b.商船学院，上海201306；2.华东理工大学信息学院，上海200237）

针对传统化工数据校正模型，文章提出了一种改进型校正模型，并对两种模型在单一平衡约束的校正效果的统计特性进行了定量分析与比较，得出了两种模型在不同工艺要求下各自的适应情况，可为数据校正工作的最佳决策提供理论依据。

数据校正；平衡约束；误差；方差

0 引言

自Kuehn和Davidson提出数据校正方法[1]以来，一直采用在满足物料、能量等平衡关系的条件下，以与对应测量值偏差的平方和最小的解作为校正值，这种校正模型一直沿用至今。目前数据校正领域的研究重点多放在如何根据传统模型选择高效的全局解搜索方法，以节省计算时间和提高搜索全局最优解得成功率，而对传统模型的校正性能很少做定量分析。本文拟在综合考虑各种影响因素的情况下，提出将平衡关系加入到校正模型中的一种改进模型，并从数理统计的角度对两种模型进行定量分析与比较，以说明两种模型各自所适用的场合。

1 传统数据校正模型简介

上世纪60年代，Kuehn和Davidson用拉格朗日乘子法求解带线性约束的最小二乘问题，从而揭开了工业过程数据校正的序幕。校正的准则为：在满足物料平衡、热量平衡、化学反应计量关系或其它物化关系的条件下，要求已测数据的校正值与其对应的测量值的偏差的平方和最小。在传统模型中，测量数据的校正值严格满足平衡约束，在采样数据中不存在大误差的情况下可以实现良好的校正结果。但是当参与校正的数据中局部测点随机误差分布的方差相对于其它测点显著较大时，而求解过程由于必须满足刚性的约束关系，导致该测点误差被硬性平摊到其它各个测点。此时若采用传统模型，相当于用大部分测点数据的劣化来换取少数测点数据的优化，从许多工程实际角度来看是一种得不偿失的校正过程。许多学者针对传统模型未考虑过失误差的问题，提出了一些解决办法。这些方法都是在数据校正之前进行显著误差侦测和处理[2][3][4][5]，但均无法确保显著误差被准确无误的侦测，导致依概率出现的大误差难以有效剔除，这些大误差对后续的校正模型的抗扰性提出了很高的要求，传统校正模型由于刚性的平衡约束关系难以适应此类情况。

2 改进模型的提出与两种模型的数学表述

为了方便统计分析与比较，设定如下前提：

（1）不同测点的测量误差相互独立；

（2）误差分布均呈高斯分布，分布参数因工况各异，分布的对称轴为理论真值。

同时为了分析时的规范，对分析过程中用到的符号形式做如下约定：

（1）测点的理论真值Xo：xo1，xo2，xo3，…，xon，n表示测点个数（注：该值在假定传感器绝对精准情况下测得，现实工艺过程中无法获得。）；

（2）测点的采样值X:x1，x2，x3，…，xn；

（5）测点的采样误差△X=X-Xo:△x1，△x2，△x3，…，△xn；

（6）平衡方程残差R:r1，r2，r3，…，rn；

（7）约束方程中各测点的正负号表示：bji，表示第j个方程的第i个测点；

2.1 传统数据校正模型的数学表述

对于传统数据校正模型有：

（1）理论平衡式：

（2）实际平衡式：

（注：由于式中各测点存在随机误差，所以存在满足随机分布的残差r）

式(2)-(1)即得到由各测点误差引起的平衡约束关系残差式:

式(3)表明，各测点随机误差的代数和造成了平衡关系式的残差，数据校正的目的就在于剔除残差R。而数据校正方案优劣的本质在于在剔除残差R的过程中，各个测点的采样误差是否也随着校正过程依一定概率缩减。

（3）校正后的平衡式：

式(4)表明，经过校正处理后得到的值应满足理论平衡约束方程。

式(4)-(2)即得到校正偏移量与残差相抵的关系式：

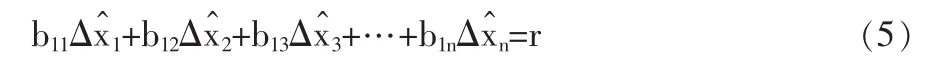
式(5)表明，校正过程本质是抵消残差，各测点数据做相应改变使满足理论平衡关系式。在最优方案中，各测点校正方向均与减小残差的方向相一致。若校正方案中出现某两个测点的校正增量相抵消，则此方案不是最佳方案。

综上所述，传统校正模型可用如下形式表述：

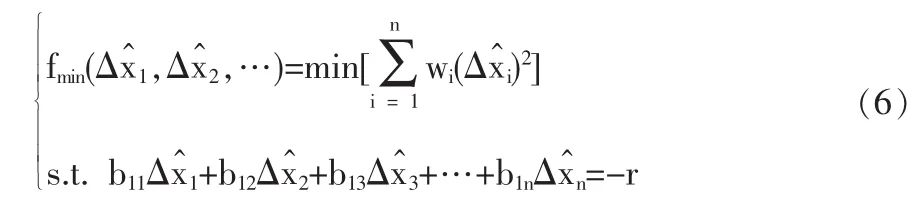
其中约束条件也可写作式(4)，两者等效。

2.2 改进模型的提出及数学表述

改进模型的主要思想是：将约束方程中的所有等式约束转化成一定条件下的不等式约束，即容许等式约束在一定范围内存在残差，将残差连同所有的约束关系放入到校正目标函数当中[6]。具体数学表述如下：

理论平衡式与实际平衡式：同(1)和(2)式。

平衡关系残差式：

校正后的平衡式：

式(8)—(10)即得到校正偏移量与残差相抵的关系式：

改进模型中△r赞为残差偏移量。与传统模型区别在于△r赞并非完全抵消掉r。这是由于传统校正模型为等式约束，要求校正解严格满足理论平衡约束方程，而新校正模型则为不等式约束，允许校正处理之后依然存留部分偏差。

由此，新校正模型可用如下形式表述：

由于改进模型的约束关系实际为不等式约束，为了方便分析，需要从形式上将式(3)～(9)改变成传统模型的形式，具体操作如下。

这样，式(12)从结构形式上与传统模型相同，只是变量的向量多出一维，意味着解空间多出一个自由度，而全局最优的解很可能在新拓宽的解空间当中。

3 两种模型性能的定量分析与比较

本文着重论述在单一约束关系情况下两种模型校正结果的统计特性。在单一约束情况下所有测点在式中的代数地位完全并列。在约束为“总校正效果刚好平衡掉方程残差”的情况下，要求每个测点为了“平衡掉残差”这个目的贡献一份力量，并且模型校正目标函数的实质要求是在总贡献固定（为相对常数r）的情况下每个测点贡献的力量要尽可能的小。由此产生一个命题：每个测点数据的贡献大小相同，并且贡献的方向均为抵消残差的方向（注：抵消残差的方向相同不等同于数据在增减方向上相同）。如果该命题成立，则每个测点的校正偏移量就可以用残差的线性函数定量的表达，每个测点校正之后的误差特性也可以定量的表达和讨论。以下为该命题的数学表述与论证过程：

当校正偏移量为-r时使fmin最小的解满足

将b1i△xi代入得到：

所以传统模型求得全局最优解时，每个测点的校正偏移量为-r/n（负号表示与残差抵消的方向，即为抵消残差做积极贡献的方向）。由上述结论可知，只要能将残差r的数值情况定量的表达出来，就可以定量的表达校正偏移量的数字特征。残差r是平衡关系中各测点误差的线性组合，各测点误差是满足相互独立的、参数各异的高斯分布：N(μi，σ2i)。的分布参数满足：

3.1 传统模型中的数字特征

3.2 改进模型中的数字特征

由前述公式可知：当且仅当等式左边各项均相等且均等于-r/(n+1)时，fmin有最小值，即当赞=r/(n+1)时，fmin有最小值。关于其中的符号，也可从工程的角度来做解释：由于残差r在校正过程中呈缩小趋势，校正后的残差赞为[0，r]区间中较为接近0点的基值，所以与r同向，而校正偏移量△赞由于是抵消r的作用，所以赞与r反向。由于

3.3 两种模型数字特征的定量比较

3.3.1 所有测点方差相等或近似的情况（无局部测点方差较大的情况）

当所有测点方差均相等，即σ1=σ2=…=σn=σ，则:

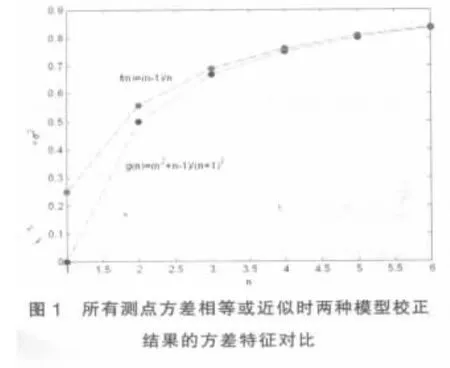
由图1可知,随测点数增加，两种模型计算结果均向σ趋近，在达到0.8σ后增幅极小，并且两种方法从n=3开始差别极小，即在测点采样值标准差相等或相近的情况下，两种模型处理结果的数字特征基本基本相同。

3.3.2 局部测点方差较大的情况

当局部测点误差的方差显著大于其他测点，即

(1)对于方差较大测点的分析

传统模型校正结果的方差特征：

由图2可见，当标准差倍数k分别等于2、3、5时（此时该测点初始方差分别为其他测点的4、9、25倍，具有广泛的代表性），随着测点数的增加，在达到0.8σ之后增幅趋缓，即对于方差显著较大的测点，传统模型约以0.7～0.8的比例将该点随机误差减小。

改进模型校正结果的方差特征：

根据式（21）与（22），两种模型的方差差异如下:

由图3可见，就该测点而言，传统模型校正后的误差小于改进模型。这是由于传统模型为了保证严格的平衡约束关系，将该测点的误差硬性分摊到其他测点上，而改进模型则相对较好的防止了大误差测点的误差扩散。

(2)对于其它测点的分析

传统模型校正结果的方差特征：

改进模型校正结果的方差特征：

根据式（24）与（25），两种模型的方差差异如下:

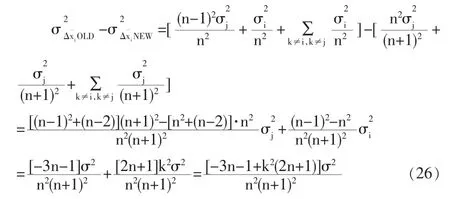
由图5可见，对于其他测点，传统模型校正后误差的方差均大于改进模型，证实了传统模型将大误差测点的误差分摊到其他测点上，使整个系统的测点均受到明显污染，而改进模型则相对稳健一些。

4 结论

本文应用概率论及数理统计的方法较为详细地定量分析并推理了两种校正模型在单一约束关系下采样数据随机误差分布情况不同时的校正效果，根据概率统计理论得出的定量结论可以看出，改进模型以一定理论和操作上的优势：

（1）方便运用启发式算法进行可行解的搜索。传统模型求解过程要求校正解严格满足平衡约束关系。当平衡关系中部分解向量确定后，剩余向量由于与这些向量之间存在由平衡约束关系决定的相关关系而被确定下来，被随之确定的向量可能严重偏离原始采样值，却无法自行纠正。这使得求解过程捉襟见肘，实际操作中很难顾全所有变量。而改进模型把等式约束转化成为不等式约束，并将不等式的“倾斜程度”作为优化目标中的一个参考量，不但与传统模型等效，而且在生成解向量的过程中，维与维之间互不约束，拓展了求解空间，使求解过程更容易运用各种优化算法，只在评判解的适应度环节中将劣质解筛除。

（2）避免个别测点依概率产生的大误差过分污染其他测点。传统校正方法会有预处理环节，校正之前对显著误差进行甄别，但无法确保能将所有显著误差甄别出来。当甄别后的数据中依然存有显著误差时，如果采用传统模型，由于必须满足刚性的约束关系，误差无法避免地平摊到其他测点中。改进模型的优势便在于，平衡约束将发挥积极的“吸能”效用，将误差的一部分吸入不等式约束关系中，以避免其他测点数据受到直接的冲击。

综上所述，通过对两种模型性能的统计特征定量分析，可知改进模型更易于进行编程求解，在各测定误差统计特征相近时与传统模型等效，并在局部测点误差较大时，校正效果明显优于传统模型,可为化工生产决策提供更加科学的决策支持。

[1]Kuehn,D.R,Davidson H.Computer Control:Mathematics of Control [J].Chem Eng Prog,1961,7(6).

[2]Madron F,Veverka V[J].AIChEJ.,1992,38(2).

[3]袁永根.化工过程测量数据校正的序贯模块算法[R].第四届化工过程的数学模拟分析年会,1993.

[4]王希若,荣冈.高置信度的显著误差综合检测法[J].仪器仪表学报, 2000,21(2).

[5]叶蕾,侍洪波.动态过程的数据校正和过失误差的侦破[J].世界仪表与自动化,2005，（9）.

[6]陈晶.电厂数据在线校正系统建模及误差特征的研究[D].华东理工大学硕士学位论文,2009.

（责任编辑/亦民）

TP274

A

1002-6487（2011）05-0004-04

延树港（1970-），男，山东东营人，博士研究生，研究方向：交通信息数据处理。