SARIMA模型在预测中国CPI中的应用
张健
(上海政法学院经济管理系,上海201701)
SARIMA模型在预测中国CPI中的应用
张健
(上海政法学院经济管理系,上海201701)
文章考虑中国通货膨胀率月度频率数据本身所表现出来的波动特征,分别对CPI同比序列和环比序列建立时间序列SARIMA模型进行了分析和预测,可为政策制定者相机抉择调控经济运行的宏观政策提供可靠工具。结果表明:相对于单一的对同比序列和环比序列建模预测而言,结合两种模型构造的合成预测值的预测精度更高。
通货膨胀率;预测;SARIMA模型
0 引言
作为通货膨胀率的衡量指标,国内外研究一般采用居民消费价格指数(CPI)或国内生产总值(GDP)缩减指数。CPI是反映居民家庭购买生活消费品和支出服务项目费用价格变动趋势和程度的相对数,是对固定的一篮子消费品价格的衡量,比较全面地反映了消费市场价格的变动,具有较强的时效性和国际可比性。GDP缩减指数的概念与CPI类似,但它的计算基础比CPI更广泛,涉及全部商品和劳务,除消费外,还包括生产资料和资本、进出口商品和劳务等。通货膨胀率是宏观经济分析和决策,价格总水平监测和调控以及国民经济核算的重要指标。这一指标不仅影响着政府制定货币、财政、消费、价格、工资、社会保障等政策,同时也与居民日常生活密切相关。从微观层面的角度来看,不同经济主体对通货膨胀率的预期及其基于预期所采取的经济行为会对不同行业的供给与需求产生不同的冲击;从宏观层面的角度来看,稳定的物价水平和宏观经济环境不仅有利于投资和经济增长,也有利于社会的和谐统一发展。货币政策从制定到产生效果所经历的时间较长,使得针对已出现的通货膨胀率水平采取政策存在时滞,往往加剧了经济的波动。因此,准确的预测通货膨胀率并相机抉择宏观经济政策是提高货币政策效果,避免经济过度波动的有效途径。
本文将通过分析通货膨胀率序列的特征,针对作为衡量通货膨胀率重要指标的CPI同比序列和环比序列分别建立SARIMA模型并对比预测精度,得出适合中国通货膨胀率预测的时间序列模型进行下一期预测,从而为政策制定者提供可靠的决策依据。
1 问题的提出
长期以来,不仅宏观政策的制定者密切关注着CPI的高低及其走势,而且很多学者也围绕着对CPI的预测进行了大量的理论和实证研究。目前,对通货膨胀率预测的方法主要分为两大类:一类是通过统计途径的调查分析得出对未来通货膨胀的预测,包括以经济学家为调查对象的Livingston预测法和以家庭为调查对象的Michigan预测法;另一类是通过计量经济学建模途径得到通货膨胀率的预测值,包括时间序列方法、联立方程模型方法和结构模型方法。
第一类方法主要是通过发放问卷或电话调查的方式对既定样本进行调查,得出他们对未来通货膨胀的预测,将样本的预测数据取算数平均最终得到未来通货膨胀的预测值。肖争艳、陈彦斌(2004)根据中国人民银行《居民储蓄问卷调查系统》的定性数据,分别运用差额统计量法和概率法将调查得到的定性数据转换为定量的预期通货膨胀,从而实现定量的预测。此类方法得出的预测结果往往滞后于实际通货膨胀发生的水平,同时,如果调查的规模过小,结果的可信度会受到质疑;大规模的调查虽然可以反映市场的预期,但是需要大量的时间和人力。
第二类方法主要基于经济理论和计量经济学方法对通货膨胀率及相关变量序列建立回归模型,利用样本数据进行预测。
时间序列模型利用经济变量自身过去的值,也可以根据其误差项的当前及过去的值中所提供的信息来建立模型并做出预测,包括自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型、自回归积整移动平均(ARIMA)模型、线形趋势法等。刘金全(2002)利用ARMA(mn)一GARCH (p,q)模型描述我国通货膨胀率的变化,发现我国通货膨胀率序列当中存在显著的条件异方差性,这说明前期通货膨胀变化程度具有一定的滞后影响。叶阿忠、李子奈(2000)采用1993年4月到1998年11月68个月的月度资料,建立GARGH(1,1)摸型,发现GARCH(1,1)模型较好地拟合了通货膨胀序列,其估计结果明显优于AR模型。王少平、彭方平(2006)利用SETAR模型对我国通货膨胀率进行了研究,在研究中国通货膨胀问题上,SETAR模型无论在拟合优度还是预测的效果上,都优于AR(p)模型。时间序列模型不依据经济理论,利用经济变量自身过去的值,也可以根据其误差项的当前及过去值中所提供的信息来建立模型并做出预测,利用外推机制描述时间序列的变化。通货膨胀率预测模型的建立与使用不是建立在关于变量的行为模式的任何理论模型基础上的,而是从观测到的数据中实证地获得其特征模型,能够较好的捕捉通货膨胀率序列的动态变化特征,因此,其应用也最为广泛。
联立方程模型主要是通过不同经济部门的影响因素构造若干模块的分支模型,将各分支模型联立组成预测通货膨胀的宏观模型。20世纪60年代,美联储开发了著名的MPS模型,用于对国内经济的分析和预测。目前,英格兰、美国、澳大利亚、德国、芬兰、加拿大、新西兰、日本等国都建立了自己的宏观经济模型。联立方程模型对于宏观经济的运行的理解比较全面和深刻,在一定程度上可以模拟宏观经济的运行并做出预测,提供政策建议。但是其预测通货膨胀率的精度却不能令人满意,同时由于模型构造复杂、数据缺乏,使得这种方法的应用受到很大限制。
结构式模型试图使用解释变量的当前值或者过去值的变动来解释因变量的变化模型。赵昕东、许志宏(2007)基于P-Star指示器对通货膨胀率进行预测。Athanasisi Orphanides和Simon Van Norden(2002)使用产出缺口建立多变量模型来预测通货膨胀率。芝加哥大学的Paul Edelstein(2007)使用贝叶斯模型,因子模型等方法预测通货膨胀率,认为这些方法都比单纯的使用通货膨胀率序列进行自身预测效果好。从增长理论上来说,结构式模型能够较好的模拟通货膨胀率与其它变量之间的关系,但是其模型的建立需要相关变量丰富的历史数据,同时除非解释变量中全部为滞后变量,否则模型对于通货膨胀率样本外的预测通常是无效的。
当建立结构式模型和联立方程模型不合适的时候,建立时间序列模型也许是合适的,因为某些引起因变量发生变化的自变量也许是不可观察或无法测度的,或者这些变量的观测频率比因变量低。这时就可以建立时间序列模型来代替结构式模型和联立方程模型。
2 模型及数据描述
SARIMA模型来源于自回归单整移动平均模型(ARIMA),博克斯和詹金斯(Box and Jenkins,1970)针对季节时间序列的方法是,首先对yt作各种不同的差分变化,然后再分析经变换后的序列的偏自相关函数(EACF)。一般说来,总是反复对序列作差分运算,直到其EACF表现出某类易于解释的特征,即只有少量的相关系数显著时为止。由该种方法最后所确认的ARIMA模型,由于通常包含周期性滞后期的有关参数,因此就常常被称为季节ARIMA模型,即SARIMA模型。典型的情况是,考虑序列yt,△1yt,(△1yt)e,△syt和△1△syt的EACF,这里(△1yt)e指△1yt对S个季节亚变量回归后的残差时间序列。而双重差分△1△s就相当于变换yt-yt-1-yt-s+yt-s-1。
SARIMA模型是表述最全面的时间序列预测模型,其他的模型都可以由它简化变型后得到。其建模思想是,将预测对象随时间推移而形成的数据序列看作一个随机序列,时间序列是一组依赖时间t的随机变量,构成该时间序列的单个序列值虽然具有不确定性,但整个序列的变化却是有一定的规律性,可以用数学模型近似描述的。这组随机变量所具有的依存关系或自相关性表征了预测对象发展的延续性,而一旦这种自相关性被相应的数学模型描述出来,就可以从时间序列的过去值预测其未来值,通过SARIMA模型可以消除趋势性和季节性,转化为平稳时间序列进行建模。
本文采用1990年1月至2010年2月CPI月度同比序列和环比序列,分别构建相应的SARIMA时间序列模型,与ARI模型的预测精度进行对比,考察SARIMA模型在预测中国CPI的应用。首先,将整个CPI序列分为两部分,利用1990年1月至2009年6月的CPI数据估计模型参数,再利用2009年7月至2010年2月的CPI数据评估模型预测精度。有关CPI相关数据来自于《中国统计年鉴》1991~2009、《中国经济景气月报》2000.4~2009.12及中国国家统计局网站。
从图1的中国CPI月度同比序列中可以发现,CPI在1992~1997年期间处于波峰阶段,最大值达到127.70。CPI同比序列波动较大,同时其波动存在非对称性,表明可能存在随机趋势。可以考虑对数据取一阶差分消除随机趋势。
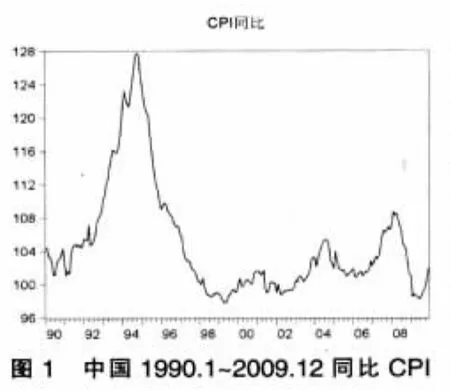

图2是中国CPI月度环比序列,环比数据的数据生成过程和波动形态与同比数据截然不同,表明存在明显的季节性因素,因此需要进行季节调整以去除季节性因素,可以考虑对数据进行12阶差分。从图中还可发现,环比CPI在1997年以前波动幅度较大,而1997年以后处于窄幅波动的状态,这与当时所采取的稳健的财政政策和货币政策紧密相关。
时间序列模型的建立要求序列必须是平稳序列,因此,在建立模型前,首先对CPI同比序列和环比序列的原始数据进行ADF单位根检验,检验结果见表1。
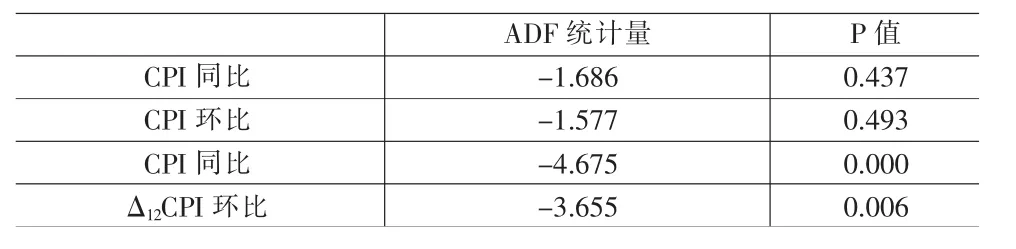
表1 中国CPI单位根检验结果
CPI同比及环比序列检验统计量的p值分别为0.437和0.493,表明序列非平稳存在单位根;对CPI同比序列和环比序列分别进行1阶差分和12阶差分季节调整,再进行ADF单位根检验,检验统计量的p值分别为0.000和0.006,表明序列经过差分后平稳,因此需要分别对数据进行1阶差分和12阶差分后才能建立回归模型。
其次,基于1990年1月至2009年6月CPI同比及环比数据,使用普通最小二乘法分别估计时间序列模型,比较AIC和SC信息准则得到通货膨胀率回归的最佳模型如下:
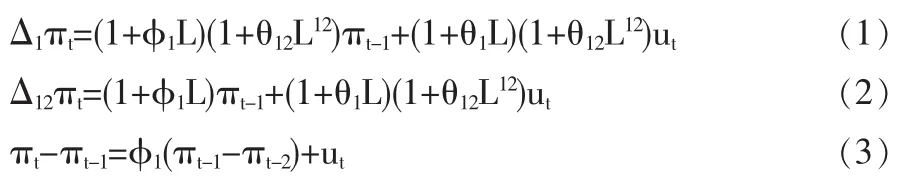
其中,πt为CPI原始数据,L为滞后算子,△为差分符号,ut为误差项,准和θ为模型参数。模型(1)为依据CPI月度同比序列所建立的ARIMA回归模型,模型(2)为依据CPI环比序列所建立的SARIMA回归模型。模型(3)为用于比较预测精度的ARI回归模型。
最后,回归两个模型的参数估计结果如表2。

表2 参数估计结果
从回归结果中可以观察到,各系数均高度显著,模型(1)的拟合程度较低但是残差和较小。应用上述模型对2009年7月至2010年2月同比CPI和环比CPI进行下一期预测,检验模型的预测精度。预测结果见表3和表4。
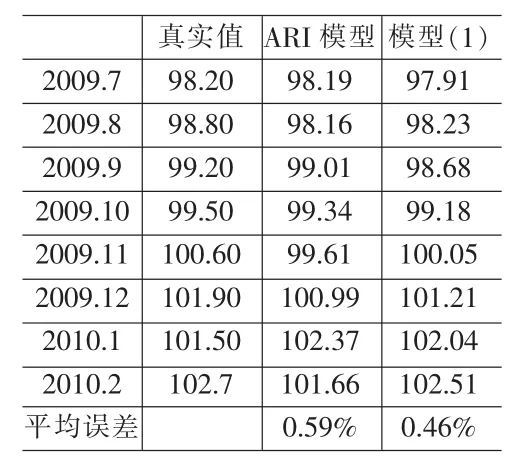
表3 2009.7~2009.12月同比CPI预测结果
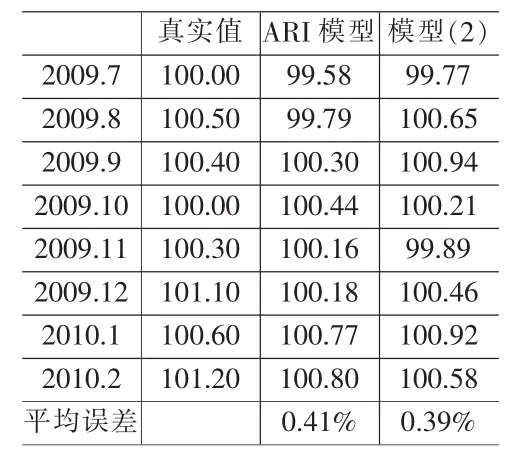
表4 2009.7~2009.12月环比CPI预测结果
从表3中的预测结果可以看出,SARIMA模型预测同比CPI的效果较好,8个月的平均预测误差仅为0.46%,小于ARI模型的0.59%。利用模型(1)预测2010年3月CPI为102.70,同比增长2.70%。
表4中模型(2)对CPI环比序列的8个月平均预测误差为0.39%,小于ARI模型的0.41%。预测2010年3月CPI环比下降0.25%。
对比两组模型的预测误差发现,SARIMA模型预测精度较高,为比较两个SARIMA模型的预测能力,现在将环比序列转化成同比序列来比较预测精度,结果见表5。
表5中利用CPI环比数据预测同比数据的平均预测误差为0.38%,预测2010年3月CPI同比增长2.87%。如果将两个模型的预测值取简单算数平均后,得到的平均预测误差下降为0.31%,预测误差下降比较明显。因此,以平均误差作为衡量预测精度的指标,应该采用综合两个模型预测值的方法预测中国通货膨胀率。预测得到2010年3月CPI同比增长2.79%。
3 结论
通货膨胀率作为反映一国宏观经济运行的重要指标,其变化趋势受到不同经济主体的广泛关注。选择合理的指标,运用合适的方法预测通货膨胀率,对政策制定者把握宏观经济走向,相机抉择财政政策和货币政策起至关重要的作用。本文考虑通货膨胀率序列的动态特征,分别对中国CPI同比及环比序列建立时间序列SARIMA模型进行分析和预测。结果表明,SARIMA模型预测精度要高于ARI模型,相对于单一的对同比序列和环比序列建模预测而言,将两者结果取平均值所构造的预测值的预测精度更高。考虑预测误差的动态影响,利用综合模型预测2010年3月中国CPI同比增长2.79%。
从CPI近期的变化趋势判断,目前通货膨胀率正处于上升周期,但当前的通货膨胀率水平还没有超过3%的警戒水平。考虑到国内经济尚未完全复苏和国际社会要求人民币升值的大环境,需要保持当前适度的货币政策不变。一方面,可以继续刺激国内投资和消费需求的增长,进一步恢复经济;另一方面,可以保持人民币汇率的稳定并抑制预期人民币升值的投机行为,避免由资产价格波动造成的经济危机。
[1]Paul Edelstein.Commodity Prices,Inflation Forecasts,and Monetary Policy[C].Working Paper,2007,(1).
[2]程建伟.通货膨胀预测的几种方法[J].价格理论与实践,2006,(3).
[3]刘金全.我国通货膨胀路径的对称性和波动性分析[J].中国管理科学,2002,(6).
[4]肖争艳,陈彦斌.中国通货膨胀预测研究:调查数据方法[J].金融研究,2004,(11).
[5]叶阿忠,李子奈.我国通货膨胀的GARCH模型[J].系统工程理论与实践,2000,(10).
[6]赵昕东,许志宏.基于P-Star指示器的通货膨胀预测模型及应用[J].数量经济技术经济研究,2007,(10).
(责任编辑/亦民)
F064.1
A
1002-6487(2011)05-0028-03
上海高校选拔培养优秀青年教师科研专项基金资助项目(SZF09001);上海政法学院院级科研课题项目(SZ09007)
张健(1979-),男,吉林长春人,讲师,研究方向:经济计量分析与预测。

