金属橡胶减振器滞迟特性研究

赵燕萍，赵子龙，张瑾瑾

（1.太原科技大学，太原 030024；2.榆林学院，陕西 榆林 719000）

金属橡胶减振器是一种典型的非线性隔振器，具有明显的滞迟效应，恢复力与元件的变形历史有关，这种强非线性阻尼性能一直是非线性理论领域研究的重点和难点，国内外学者对金属橡胶的阻尼特性进行了大量的研究［1-4］，目前还没有比较完善的模型。通过实验可以有效获得特定金属橡胶构件的阻尼耗散特性，但不具有通用性；在滞迟振动系统的运动微分方程中单纯采用数学模型，不能够揭示相应的干摩擦元件的物理行为。因此，探索描述系统滞迟回线的新方法，提高建模精度，具有重要的意义。本文利用金属橡胶减振器的悬臂梁模型，推导出恢复力与变形的关系，对相对密度不同的环形金属橡胶减振器，运用ANSYS有限元分析软件进行数值模拟，解析得到的与数值模拟得到的滞迟回线进行比较，验证了理论推导得到的解析表达式是正确的。

1 金属橡胶滞迟特性的理论分析

1.1 力学模型的建立

金属橡胶的力学模型采用悬臂梁杆系模型［4］，如图1所示。空载时各托架间的间隙相等，加载状态下外载荷作用到第一个托架上，托架由上而下挨个接触，随着参与接触托架数目的增加，杆系整体刚度表现出非线性增大的趋势。

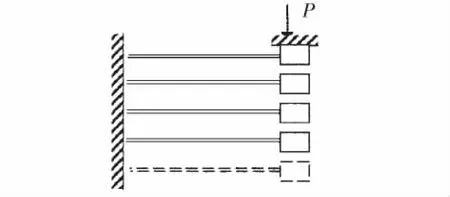
图1 金属橡胶悬臂梁杆系模型Fig.1 Cantilever beam trussing model of MR

杆系变形时作如下假设:

①元件为只承受弯曲变形的等直梁；

②能量靠元件在接触处的相互移动来耗散；

③元件间的接触力以正压力和摩擦力形式出现；

④接触表面的摩擦力由库仑定律确定T=fP.

金属橡胶减振器可看作是由彼此串联和并联的杆系形成的结构阻尼系统。

1.2 加载过程分析

第一加载阶段，模型如图2所示，从第一个元件受力P的作用，到与第二个元件接触前，第一个梁的挠度与P的关系为:

其中:h为托架高度，y为托架1和托架2之间的最大间隙，EJ为梁的抗弯刚度。

图2 单个元件的横向弯曲Fig.2 Single component bending

同理可得出第i个元件的挠度与P的关系为:

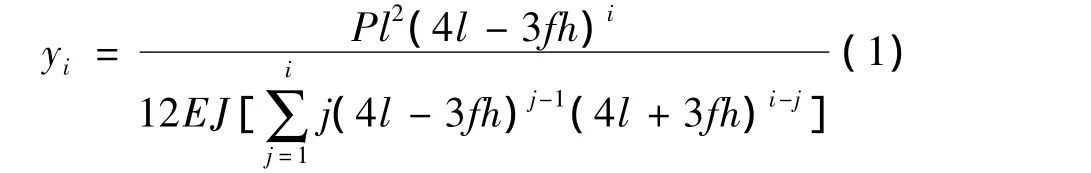
1.3 卸载过程分析

卸载过程中，托架作为整体组合梁，如图3所示。

图3 横截面切应力计算图Fig.3 Shear stress on cross section

任一横截面上作用的切应力为:

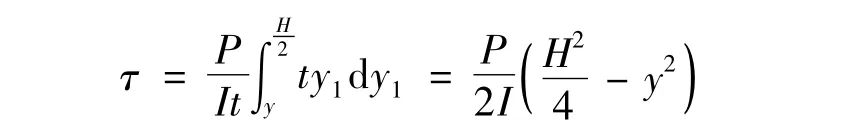
距中性层为y处以下部分切应力合力为:

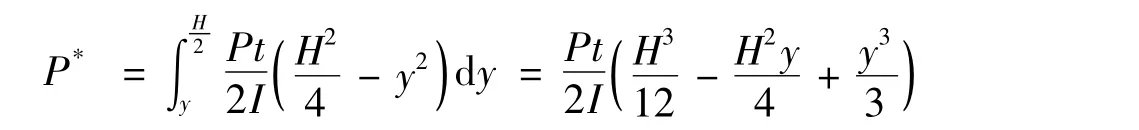
第一卸载阶段，从n个托架全部接触到与第n个托架分离。假设组合梁由n个托架构成，如图4所示。

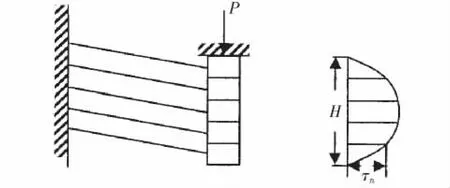
图4 杆系卸载计算图Fig.4 Unloading diagram of trussing

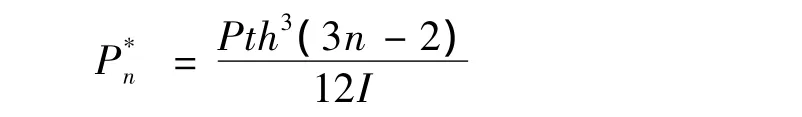
卸载过程中各托架受压缩载荷和摩擦力作用，摩擦力方向与加载过程相反，卸载开始时，第n个梁的挠度为:

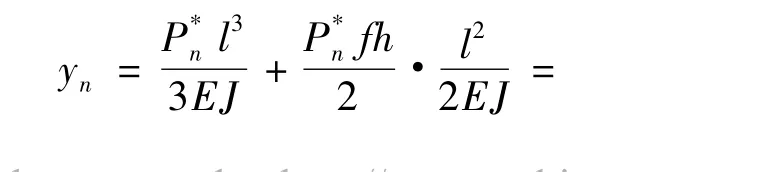
同理，第n-i+1个梁的挠度与P的关系为:

2 金属橡胶滞迟特性的数值模拟

假设金属橡胶试件由边长为dz的正方体单元构成，则试件可分为n层，每层单元体相互串联，n=每层由m个单元体组成，各单元体相互并联，m=HMR为金属橡胶试件高度，SMR为金属橡胶的成型受压面积。

金属橡胶试件的总体位移:

弹性恢复力关系为:

ΔHe为单元体在受压方向的位移；Fe为单元体的弹性恢复力。

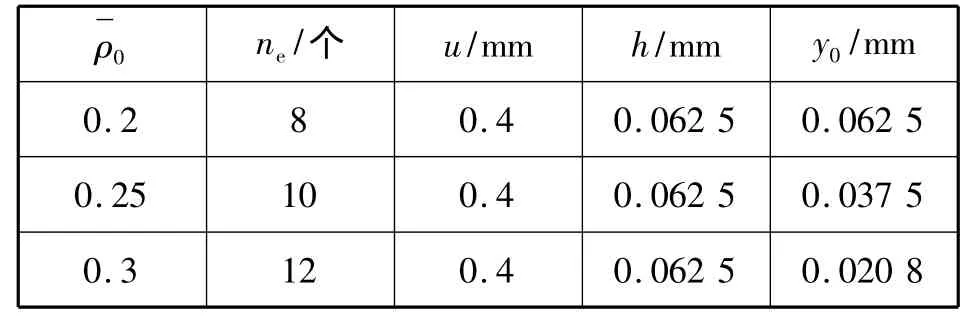
表1 试件的悬臂梁模型尺寸参数Tab.1 Sizes parameters of cantilever trussing model

试件相对密度在0.2～0.4之间变化时其弹性性能比较稳定，其性能最可靠，随着载荷的继续增大不可恢复变形急剧增加［5］。假定发生最大变形时所有线匝都参与接触滑移，空载时每个单元体包括线匝数目ne等于每组悬臂梁的个数，ne=

其中，ds为金属橡胶试件的丝线直径为金属橡胶试件空载时的相对密度。

对金属丝直径ds为0.1 mm，螺旋匝线中径dz为1 mm的三种相对密度的环形金属橡胶减振器进行有限元分析。试件外形尺寸均为Φ32×20×6，相对密度分别为 0.3，0.25，0.2.取受载上限为最大有效弹性变形值，其相对密度为0.4，悬臂梁的长度取l=2.9 mm.，其他参数如表 1［6］所示。

为控制模型变形范围，在模型最下边的托架下方y0处添加一个托架固定，设定边界条件:

①选用面面接触类型，在相邻的两托架间定义接触对；

②在悬臂梁根部和另加托架各自由度施加固定约束。

利用所给单元体，对相对密度分别为0.2、0.25、0.3的试件的加载和卸载过程分别进行数值模拟。

3 金属橡胶滞迟回线理论分析结果与数值模拟结果对比

将数值计算得到的单元体在受压方向的位移ΔHe和Fe弹性恢复力代入式（3）和式（4）求得变形量ΔH和载荷F，利用最小二乘拟合得到相对密度为0.2，0.25，0.3 的金属橡胶试件的滞迟回线，再分别对相对密度分别为 0.2、0.25、0.3 的试件利用式（1）和式（2）得到各阶段的恢复力和受压方向的位移，代入式（3）和式（4）求得变形量ΔH和载荷F，获得加、卸载过程三种相对密度金属橡胶试件的滞迟回线，与数值模拟结果相比较。比较结果如图5-图7所示。

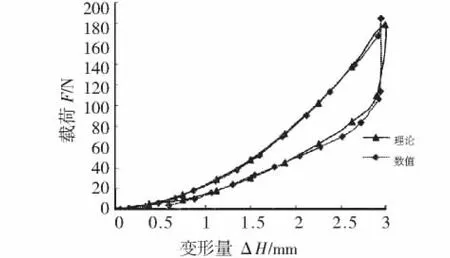
图5 金属橡胶滞迟回线的比较=0.2）Fig.5 MR comparison of hysteretic loop=0.2）

图6 金属橡胶滞迟回线的比较（=0.25）Fig.6 MR comparison of hysteretic loop=0.25）

图7 金属橡胶滞迟回线的比较=0.3）Fig.7 MR comparison of hysteretic loop=0.3）

从图5-图7中可以看到，理论计算和数值模拟两者得到的金属橡胶试件的滞迟回线特性基本一致，说明本文采用的理论模型得出的计算结果是正确的。同时可以看到=0.2时，金属橡胶的耗能特性最大，且其刚度最小，软特性阶段最宽。

4 结论

通过对滞迟回线的分析可得出以下结论:

（1）金属橡胶的滞迟回线特性理论计算和数值模拟的结果基本一致，表明本文采用的理论模型得到的计算公式是正确的。

（2）金属橡胶的成型相对密度越小耗能特性越大。

（3）金属橡胶材料的相对密度越小，其刚度越小，软特性阶段越宽，与文献［7］的实验结果相符。

［1］邓剑波.悬臂梁根部金属橡胶减振器阻尼性能的实验研究［J］.航空动力学报1998，13（4）:406-408.

［2］郭宝亭，朱梓根，崔荣繁，等.金属橡胶材料的理论模型研究［J］.航空动力学报.2004，19（3）:314-319.

［3］姜洪源，夏宇宏，敖宏瑞.金属橡胶构件的性能分析与实验研究［J］.中国机械工程，2001，12（11）:294-297.

［4］（俄）切戈达耶夫.金属橡胶构件的设计［M］.李中郢，译.北京:国防工业出版社，2000.

［5］Чeroдаeв Д E，Myлюκии O H，Kолыгин E B.Kонстpyиpoванниe poōoчнних oprанов мшин иoóopyдованиия и3 ynpyгonopиcтoгo матepиала мp［M］.Cамаpа:Cамаpcкий rocyдаpcтвeнный аэpoкоcмичecкий yнивecтитeт，1994.

［6］李明森，张文群，吴新跃.金属橡胶的悬臂梁杆系模型及有限元分析［J］.机械与设计，2008，10:15-18.

［7］陈艳秋，郭宝亭，朱梓银.金属橡胶减振垫刚度特性及本构关系研究［J］.航空动力学报，2002，17（4）:416-420.