一种混合一维搜索的矢量拟态物理学算法

张 斐，谢丽萍，曾建潮，谭 瑛

（太原科技大学复杂系统与计算智能实验室，太原 030024）

目前工程实践中涉及到很多约束优化问题（Constrained Optimization，CO），如机械设计、生产调度、交通调度、资金使用、工程参数控制等问题。约束优化问题的实质是在自变量满足约束条件的情况下，求解目标函数最优解的全局优化问题，由于约束条件的存在，使求解约束优化问题比较困难。传统的解决约束优化问题方法的有:惩罚函数法［1］、可行规则法［2］、约束保持法［3］、牛顿法［4］。自各种启发式优化算法提出以来，混合约束保持法的微粒群算法［5］、混合惩罚函数的遗传算法［6］、混合可行性规则的差分演化算法［7］、混合可行性规则的类电磁算法［8］、混合罚函数的微粒群算法［9］，为解决约束优化问题提供了很多新的有效解决方案。但这些算法自身也存在不足之处，例如微粒群算法容易陷入局部最优解，类电磁算法的局部搜索效率不高，由于矢量拟态物理学算法本身是全局优化算法避免出现陷入局部最优情况，而引入一维搜索方法提高了算法局部搜索可行个体信息的能力，故本文提出了混合一维搜索的矢量拟态物理学算法。

拟态物理学优化算法（Artificial Physics Optimization，APO）［10］最早由 Spear 和 Cordon［11］提出的，因受物理力学定律的启发故称为“拟态”，是一种基于拟态物理学［11］的新的全局优化算法。APO算法中每个个体可以看做是可行域内的一个可行解，通过利用一群在可行域内随机初始化产生的个体来搜索目标函数的最优解，个体的质量是用户定义的有关其适应值的函数，个体适应值越好，质量就越大，对其它个体的作用力就越大。适应值较优个体吸引适应值较差个体，适应值较差个体排斥适应值较好个体，最优适应值个体对其它所有个体都有吸引力，但不受其它个体的作用力，整个种群在这种引斥力的作用下向更好的搜索区域搜索，整个群体经历的最好位置就是当前的全局最优解。

1 约束优化问题

一般来说，约束优化问题的数学模型如下:

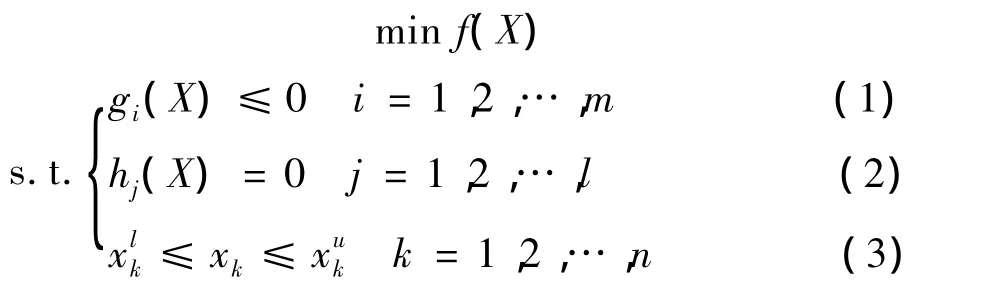
其中，X={x1，x2，…，xk，.xn}T是决策变量，n 是决策变量的维数，和是第k维分量的上下界。式（1）是不等式约束条件，式（2）是等式约束条件，式（3）是边界约束条件。X∈S⊂RN，S是式（3）表示的变量X所有可能的取值范围，称为问题空间；F是所有可行解构成的空间，称为可行域；显然F⊆S.约束优化问题就是保证变量X在满足m个不等式约束和l个等式约束前提下，寻找目标函数的最优解。

对于约束优化问题构造违反约束量函数φ（X），表达式如下:

其中 max（0，gi（X））（i=1，2，…，m）表示个体X在第i个不等式约束的违反程度，|hj（X）|（j=1，2，…，l）表示个体X在第j个等式约束的违反程度。违反约束量函数φ（X）表示个体X到可行域的距离，若φ（X）=0表示个体为可行个体，φ（X）＞0表示个体为不可行个体。

2 VM-APO算法

APO算法目前在解决无约束优化问题上已经有了很多研究成果，包括:个体之间的负指数作用力规则、单峰函数作用力规则、线性作用力规则三种作用力规则对APO算法性能的影响［12］；个体质量函数应具有的的性质及构造方法［13］；通过借鉴生物个体的记忆和交互能力提出的扩展的拟态物理学优化算法［14］；以及矢量拟态物理学优化算法（The Vector Model of Artificial Physics Optimization，VMAPO）模型［15］。但目前APO算法仍未用于求解约束优化问题，本文采用矢量拟态物理学优化算法结合一维搜索方法求解约束优化问题，个体的速度和位置作为矢量处理。通过引入收缩系数β*处理个体越界问题，以确保个体移动后始终在问题空间内；然后用违反约束量函数来判断个体是否在可行域内，利用一维搜索方法使跳出可行域的个体回到可行域内。

以求解无约束全局最小化问题为例，整个种群的集合为A=（X1，X2，…，XNpop），其中Npop为种群个体数量，个体 i的位置矢量 Xi=（xi，1，…，xi，k，…，xi，n），速度矢量 Vi=（vi，1…vi，k…vi，n），其中 n 为解空间的维数，VM-APO算法由三个部分组成:初始化，计算个体所受作用力，个体运动。算法框架如下:

首先初始化种群，个体的初始位置和速度都在n维问题空间中随机产生，计算每个个体的适应值，取得最优适应值的个体被标记为Xbest.

咳嗽跟呼吸的空气有很大关系。如果空气太脏，或者是太干燥，宝宝就咳得厉害。所以，在家里护理宝宝时，若天气好，应多开门窗通气，使屋里的空气保持清新；若天气不好，可以使用空气净化器来改善室内的空气；若空气干燥，要用加湿器增加室内湿度，使用加湿器使室内湿度保持在40%～50%，湿度太大也不行，容易使房间滋生霉菌。也可以选择让宝宝吸入水蒸汽的方式缓解咳嗽。睡前在浴室内放会儿热水，待蒸汽充满浴室，把宝宝抱进去尽可能多待一些时间，让呼吸道通过多吸入一些水蒸汽获得充分的滋润，这个方法也有助于缓解鼻塞和咳嗽。还可以用妈妈们蒸脸的蒸汽机让宝宝的呼吸道滋润，但蒸汽机里不能使用自来水或矿泉水，要使用蒸馏水。

接着计算个体所受作用力，要计算个体所受力，首先计算个体的质量，质量函数是关于适应值的反比例函数，即个体i的适应值越小，其质量就越大。算法中质量函数可构造为:

其中Xbest是取得最优适应值的位置，Xworst是取得最差适应值的位置。

由于VM-APO算法定义了矢量模型，所以若定义Ni={Xj|f（Xj）＜ F（xi），∀Xj∈A}，为相对个体i较好个体的集合，Mi={Xj|f（Xj）≥f（Xi），∀Xj∈A}为相对个体 i较差个体的集合，‖Xj-Xi‖ =为个体j相对于个体i的距离。个体j相对于个体i的矢量方向表示为= ［rij，1，……rij，n］，其中:

则个体j对个体i的作用力为:

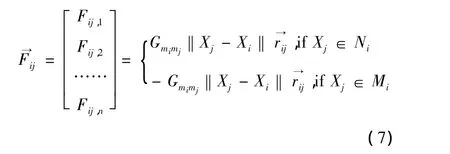
最后更新个体运动的位置和速度，个体i在t+1时刻的速度和位置迭代方程为:

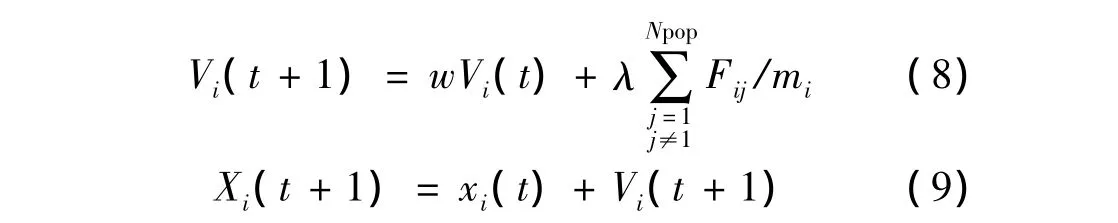
其中λ是随机变量且λ～U（0，1），w为惯性权重，w∈［0，1］.

3 VM-APO-ODS算法求解约束优化问题

本文求解约束优化问题时，首先采用约束保持法，使个体在迭代过程中都在可行域内，然后再利用VM-APO算法进行搜索找到目标函数的最优解。因此初始化种群要求产生Npop个可行个体，然而在迭代过程中，个体有可能跳出问题空间。VM-APO算法对这些越界个体的处理方法是将其拉回问题空间的上或下边界，但这种处理方法改变了个体的搜索方向，为了保存个体的速度方向这一重要信息，本文引入一个收缩系数β*将越界个体拉回问题空间，并且不改变其搜索方向。此时所有个体都在问题空间中，但有可能一些个体不在可行域内，对不可行个体采用一维搜索的方法将个体映射回可行域内。

引入一个收缩因子处理越界个体。在VM-APO算法中，种群经过迭代进化后，处理个体越界的方法如下:

由于第一种处理方法使个体运动方向会发生改变，为了保持个体的运动方向不变，在算法中引入收缩系数β*将越界个体拉回解空间。其中当个体i逃离问题空间中的第k维上界（）时，

故可知要让个体i的位置矢量Xi收缩回问题空间，只需要用最小的收缩系数β*将越界个体的分量xi，k（k=1…k…n）都拉回问题空间，即:

则个体i的位置迭代方程如下:

其中β*的取值范围为（0，1］，经过这样处理后能保证越界个体都在问题空间内。

即使采用上述方法将个体拉回问题空间，也不能确保所有个体都是可行个体，对于不可行个体用一维搜索方法在速度方向上找到可行解。首先对在问题空间内的个体，利用违反约束量函数φ（X）判断个体是否为可行个体，对于在t时刻的可行个体，若在t+1时刻不在可行域内，将在位置迭代方程中引入一个系数（如式（15）所示）α，使得在其速度方向上能找到一可行解，即使个体i在t+1时刻的违反约束量最小，如式（16）所示，这其中系数α相当于一个步长，所以α的确定过程可以用一维搜索方法来代替。

这种一维搜索方法的矢量拟态物理学优化算法（The Vector Model of Artificial Physics Optimization Algorithm with one demention search method，VMAPO-ODS），通过利用一维搜索方法，确保种群所有个体都在可行域内。

VM-APO-ODS算法具体流程如下:

Step1 初始化种群。在问题域内随机产生Npop个个体，其速度产生也是随机值，根据式（4）判断个体是否在可行域内，若在可行域内保存个体，若个体不在可行域内直接删除。计算种群个体的适应值，并选出全局最优个体bbest.

Step2 计算个体所受力

（1）利用式（5）计算个体质量。

（2）利用式（7）计算种群个体间作用力。

Step3 利用式（8）和式（9）更新个体的速度和位置。

Step4 判断个体是否越界，如果越界用式（13）计算种群个体的最小收缩系数 β*，利用式（14）将个体拉回问题空间。

Step5 利用式（4）判断个体是否在可行域内，并利用一维搜索找到个体的新位置，如果个体在可行域内则跳转到Step 6，否则，用式（15）产生新位置重新转到Step 5.

Step6 计算种群所有个体的适应值，并更新最优个体及其适应值。

Step7 判断是否满足结束条件，若满足，退出并输出最优适应值；否则，执行Step 2.

4 仿真实验

为了测试该算法的性能，利用经典Michalewicz基准测试函数［16］来进行仿真测试，将VM-APO-ODS算法与文献［8］中的FAD-ELM算法在同等条件下进行比较，VM-APO-ODS算法中采用黄金分割法来实现一维搜索过程，其中参数选取为:在式（7）中λ是随机变量且 λ ～U（0，1），w∈［0.4，0.9］，w 是随着时间t线性递减变化的函数，w的公式为:

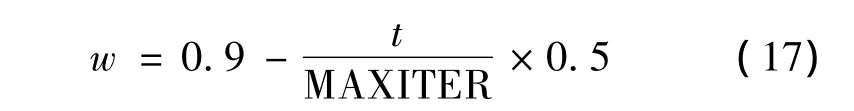
其中MAXITER为最大迭代次数。在仿真试验中发现参数G的取值对VM-APO-ODS算法的性能影响较大，并且以下10个测试函数的G的取值取经验值。

表1 VM-APO-ODS算法与FAD-ELM算法比较最优适应值和平均最优适应值Tab.1 The comparison of VM-APO-ODS with FAD-ELM on the results of optimal fitness and average optimal fitness

VM-APO-ODS算法与FAD-ELM在相同实验条件进行测试，选用个体50个，实验独立运行30次，每次实验的最大迭代代数为7000，实验结果如表1所示。在测试 g01、g04、g06、g07、g10 时，VM-APOODS算法在最优适应值、平均最优适应值上都优于FAD-ELM算法。在测试 g02、g09、g11时，VM-APOODS算法在最优适应值上优于FAD-ELM算法，在测试函数g12时两个算法在最优适应值上都能达到已知最优解，本算法在平均最优适应值上要略低于FAD-ELM算法。从表1中还可以看出VM-APOODS算法在测试函数g01、g04、g11、g12都能找到已知最优解，在测试函数 g02、g06、g07、g08、g09、g10都能搜索到最优解的邻域，说明算法在求解目标函数最优解上具有较好的求解性能；从方差的结果看，算法的求解结果比较稳定，实验结果表明VMAPO-ODS算法是一种有效算法。

5 结论

本文用矢量拟态物理优化算法结合约束保存法来求解约束优化问题，通过引入收缩系数处理越界问题，沿着其速度方向将其拉回问题空间，并采用一维搜索方法确保种群个体在运动过程中始终在可行域内。仿真实验表明该算法是有效的，后期工作将对VM-APO-ODS算法在求解约束优化问题时平均最优值精度的问题，通过选择不同曲线质量函数，引入多维搜索提高平均最优解的精度。针对G的取值对算法性能影响较大的问题，可对参数G的设置进行进一步的研究探讨，对于本算法运用到解决实际机械设计问题是下一步研究工作。

［1］高显忠，罗文彩，侯中喜.应用改进PSO算法求解约束优化问题［J］.计算机仿真，2009，26（10）:212-215.

［2］王凌，何碶，金以慧.智能约束处理技术综述［J］.化工自动化及仪表，2008，35（1）:1-7.

［3］SUN C L，ZENG J C，PAN J S.An New Vector Particle Swarm Optimization for Constrained Optimization Problems［J］.Computational Sciences and Optimization，IEEE，2009，5779:485-488.

［4］陈加民，陈桂榕.解一般约束优化问题的牛顿法德超线性收敛性［J］.太原科技大学学报，2010，31（5）:397-398.

［5］SUN C L，ZENG J C，PAN J S.A Particle Swarm Optimization with Reserved Average Velocity for Linearly Constrained Optimization Problems［C］//International Symposium on Management Engineering（ISME），2009:3:543-547.

［6］汪岚.基于混合遗传算法的染色优化模型与仿真［J］.计算机工程，2009，35（22）:218-220.

［7］胡中波，王曙霞，熊盛武，等.求解约束优化的自适应杂交差分演化算法［J］.计算机工程与应用，2009，45（31）:211-214.

［8］MARIA ANA，ROCHA A C.Feasibility and dominance rules in the electromagnetism-like algorithm for constrained global optimization［C］//Computational Science and Its Applications（ICCSA），2008:5073:768-783.

［9］陈加民.非线性规划问题的算法研究［D］.太原:太原科技大学，2008.

［10］XIE L P，ZENG J C，CUI Z H.General Frameworkof Artificial Physics Optimization Algorithm［C］//Proceedings of 2009 World Congress on Nature and Biologically Inspired Computing，India，2009:1321-1326.

［11］SPERAS W M，SPEARS D F，KERR W.An Overview of Physicomimetics［C］//Lecture Notes in Computer Science-State of the Art Series，2005，3342:84-97.

［12］XIE L P，ZENG J C.The Performance Analysis of Artificial Physics Optimization Algorithm Driven by Different Virtual Forces［J］.ICIC-EL，2010，4（1）:239-244.

［13］XIE L P，ZENG J C，CUI Z H.On mass effects to artificial physics optimization algorithm for global optimization problems［J］.International Journal of Innovative Computing and Applications，2010，2（2）:69-76.

［14］XIE L P，ZENG J C.An Extended Artificial Physics Optimization Algorithm For Global Optimization Problem.Proceedings of Fourth International Conference on Innovative Computing［C］//Kaohsiung，Taiwan，Information and Control（ICICIC 2009），2009.

［15］XIE L P，ZENG J C，CUI Z H.The Vector Model of Artificial Physics Optimization Algorithm for Global Optimization Problems［J］.Intelligent data engineering and automated learning，2009，5788:610-617.

［16］MICHALWEICZ Z，DASGUPTA D.Evolutionary algorithms for constained optimization parameter problems［J］.Computer＆ Industrial Engineering Journal，1996，30（4）:851-870.