圆锥杆斜侵彻水泥靶时应力波传播特性研究
王运叶,赵子龙
(太原科技大学,太原 030024)
目前,军事上许多工事已由地表转移到地下,相应地对侵彻弹提出了新的要求,深层侵彻弹的研究与应用由此而生。怎样才能发挥侵彻弹的最大作用效果,这是国内外急需解决的问题。
对于高速撞击和动力侵彻问题,已进行了大量的研究。文献[1]对垂直侵彻时的撞击力进行了研究;文献[2]研究了垂直侵彻时纵向应力波传播;文献[3]明确了经验公式的适用范围;文献[4]给出了柱形空腔膨胀条件下卵形弹体侵彻靶体深度的理论计算公式;文献[5]给出弹体减速度时间历程解析解的法向膨胀理论;文献[6]讨论了初始旋转角速度对长杆弹垂直侵彻时的撞击力和侵入位移的影响。但这些研究均未考虑斜侵彻时纵向应力波和横向应力波同时存在的应力波传播。在文献[1]和文献[2]研究的基础上,研究了撞击速度在1000 m/s~2000 m/s间的圆锥杆对半无限厚水泥靶的倾斜侵彻过程及其应力波传播特性。以比例系数的形式考虑了其它能耗对撞击力的影响。得出了与文献[7]实验基本相符的重要结论:初始侵彻角度对轴向撞击力影响非常小。
1 基本假设
为了简化圆锥杆倾斜侵彻半无限厚水泥靶板问题,先做如下基本假设:
(1)将圆锥杆侵彻过程分析与圆锥杆中应力波传播分析分开。
(2)在研究撞击的过程中,将圆锥杆视为刚体(圆锥杆相对水泥靶较硬);而在研究应力波传播的过程中,将圆锥杆的塑性动力学本构关系取为线性硬化关系且应力只是应变的单值函数。
(3)水泥靶响应区介质只沿圆锥杆撞击表面的法向运动,响应区介质获得与圆锥杆接触表面法向相同的速度(基于水泥靶材料性质用流体作近似处理)。
2 侵彻过程
建立圆锥杆与水泥靶斜侵彻的空间几何关系及两组坐标系如图1所示。一组是定坐标系Oxyz,O点与初始撞击点重合;另一组是动坐标系Cr*βz*,C为圆锥杆的质心。在讨论圆锥杆与水泥靶侵彻时,从圆锥杆与水泥靶接触开始计时。

图1 侵彻过程示意图Fig.1 The scheme of penetration
2.1 受力分析
在圆锥杆与水泥靶接触表面任一点A处取一微元dS,作用于圆锥杆微元上的法向撞击力为dF。在水泥靶微元上作用有等值反向的撞击力为-dF。水泥靶对圆锥杆的反作用力等于静抗力(强度效应引起)-σcdS和动抗力(惯性效应引起)-dFd的迭加,其中σc为水泥靶介质的挤压强度。

图2 水泥靶板微元的受力分析Fig.2 Force analysis of targer element
如图2所示的微柱,当作用于水泥靶微元dS上的dFd沿其方向运动dl时,所做的功为dFddl,同时微段AA'获得动能增量ρdSdnv2n/2,其中ρ为水泥靶介质密度,dn为微柱的法向扩展量。vn为微柱介质的法向速度。
由动能定律得到:

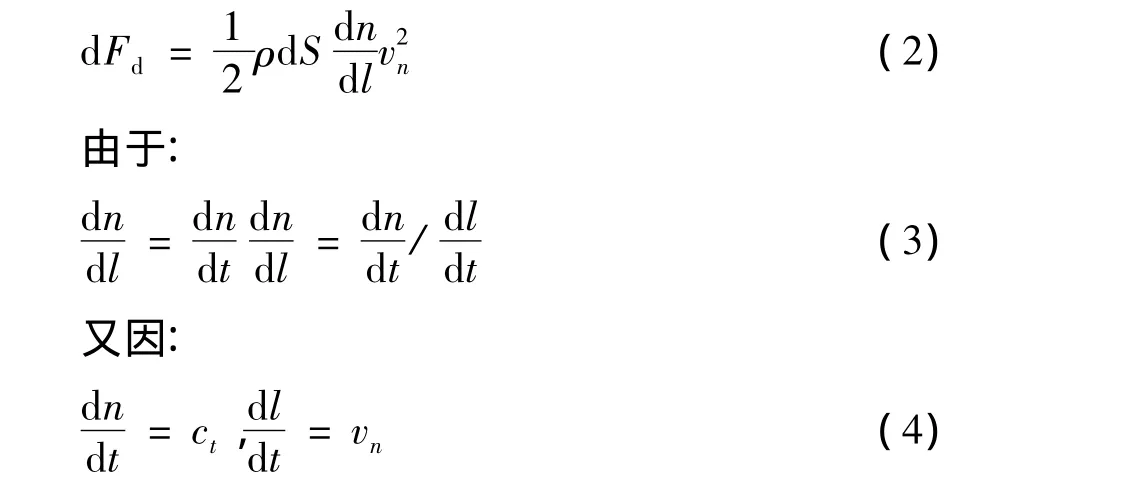
其中ct为微柱介质的法向扩散速度。则:

2.2 水泥靶板响应区域扩散速度ct的分析
因水泥及混凝土等材料的挤压传播速度较小,同时又具有可压缩性。因此响应区域的扩散速度是由未响应区域的质量密度ρ变成响应区的质量密度ρ*的扩散速度,由质量守恒定律得:

2.3 圆锥杆的动力学方程
设圆锥杆的质量为 mp,圆锥杆绕过其质心C(xc,yc)且与z轴平行的zc轴的转动惯量为Jp,由刚体平面运动微分方程得:

式中α为圆锥杆绕zc的转角,SA为圆锥杆侵入水泥靶表面面积。侵彻表面微元的法向速度vn可表示为:

2.4 圆锥杆与水泥靶侵彻过程的几何关系
在动坐标系Cr*βz*下圆锥杆表面的几何方程为:

在图1中ψ可写成:


图3 侵彻过程的空间几何关系Fig.3 The spatial geometry relation of penetration process
在动坐标系Cr*βz*下,水泥靶界面的几何方程为:
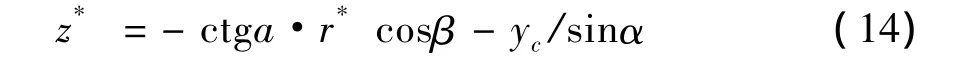
进而得出式(8)-式(10)的曲面积分:

其中R1(β)和R2(β)是方程

的两个正实根,且 R2(β)≥ R1(β).β0是使式(16)r*取重根时的β.
2.5 数值计算
动力学方程(8)-方程(10)均是二阶微分方程,可采用中心差分法和高斯6点积分求解。
由此可求得沿x和y方向的作用力fx,fy的数值解。利用力的投影规则可求得沿r*(β=0),z*方向的作用力fr和fz.
3 应力波传播
3.1 波动方程的推导
建立如图4所示坐标系,原点O1位于圆锥杆的顶部,O1x1轴与圆锥杆的轴线重合,随其一起运动。设圆锥杆任一点在纵向(x1方向)和横向(y1方向)的变形分别为u(x,t)和v(x,t),任意截面的转角为φ(x,t).

图4 圆锥杆受力分析示意图Fig.4 Force analysis of concial rod
连续方程:
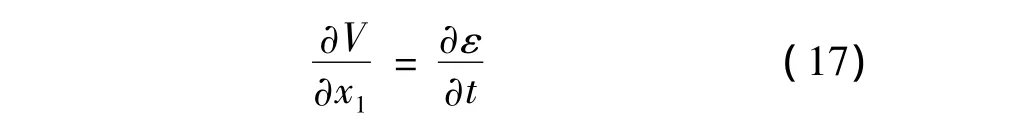
其中V为质点速度,ε为应变。
运动方程:
取微元体dx1,其受力情况如图5所示。

图5 圆锥杆受力分析示意图Fig.5 Force analysis of concial rod
由∑Fx1=mü得:

由∑Fy1=mv¨得:
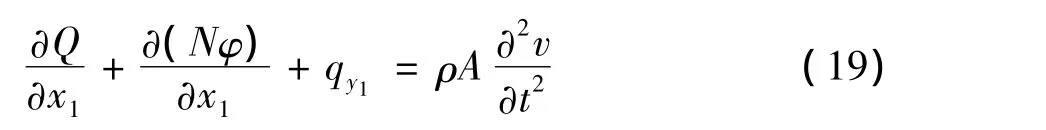
由∑Mc1=Jφ¨得:

其中N、Q和M分别表示x1处的轴力、剪力和弯矩;ρ为材料密度;A为x1处的横截面面积,其值为:A=2πhx1tgθ;J为微元体转动惯量,J= ρIdA;I为截面的惯性矩,I= πhtg3θ·;θ为圆锥杆半顶角;qx1、qy1分别表示微元体单位长度沿x1、y1方向上的惯性力,它们可表示为:

其中l1表示O1到圆锥杆质心的距离。
根据文献[8]由方程(18)-方程(20)可导出:

其中 C2=E/ρ,=Gk/ρ,C2=2C1/tgθ,E、G为材料常数,k为与截面几何形状有关的剪切常数。
3.2 初始条件和边界条件
(1)初始条件

(2)边界条件

在初始条件(24)-条件(26)中,位移和速度都是相对于动坐标系O1x1y1.
3.3 波动方程的数值计算
波动方程为非线性偏微分方程组,这里采用中心差分格式进行数值计算。求得一系列位移值即波动方程的数值解。
在求得位移的数值解后,依据应力和位移的关系,利用上述差分格式可求得应力的一系列数值解。进而得到应力的时程曲线和分布曲线,分析和研究应力波在圆锥杆中的传播特性和规律。
4 计算实例和结果分析
对圆锥杆倾斜侵彻半无限厚水泥靶的撞击力和应力波传播进行了计算与分析。取水泥的密度ρ=2.13×103kg·m-3,极限密度ρ*=2.20 ×103kg·m-3,挤压极限为σc=80 MPa,圆锥杆的质量为mp=34.5 kg,圆锥杆的几何参数分别为 R=0.050 m,θ=8°,l=0.356 m,L=1.068 m,φ =0.300 m,圆锥杆的硬化模量为E=1.26 GPa,G=E/[2(1+ μ)],μ =0.3,剪切常数k=10/9,这里假定圆锥杆的初始动能只有十分之一用于产生撞击力。由图6可以看出,初始侵彻角度对轴向撞击力影响非常小,这与文献[7]的实验结论基本相符。如图7所示,初始侵彻角度对横向撞击力的影响非常大,这与实际情况相同。在计算波动方程时,初始侵彻速度为v=1 km·s-1,初始侵彻角度为α0=75°,其它参数同前。应力的时程曲线如图8-图11所示,正应力的传播以轴向力产生的正应力为主;应力分布曲线分别如图12-图15所示,正应力的分布也以轴向力产生的正应力为主。因此合成正应力以轴向力产生的正应力为主。

图6 轴向撞击力时程曲线Fig.6 The history curve of axial force

图7 横向撞击力时程曲线Fig.7 The history curve of lateral force

图8 正应力时程曲线(轴向力)Fig.8 The history curve of normal stress(axial force)

图9 正应力时程曲线(横向力)Fig.9 The history curve of normal stress(lateral force)

图10 剪应力时程曲线Fig.10 The history curve of shear stress

图11 合成正应力时程曲线Fig.11 The history curve of resultant normal stress
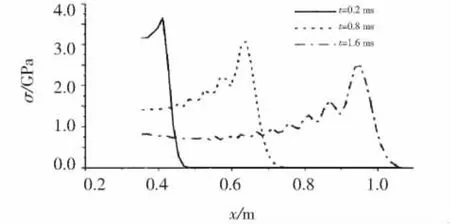
图12 正应力分布曲线(轴向力)Fig.12 The distribution curve of normal stress(axial force)

图13 正应力分布曲线(横向力)Fig.13 The distribution curve of normal stress(lateral force)

图14 剪应力分布曲线Fig.14 The distribution curve of shear stress

图15 合成正应力分布曲线Fig.15 The distribution curve of resultant normal stress
5 结论
(1)初始侵彻角度对轴向撞击力影响非常小,但对横向撞击力的影响非常大。
(2)当初始侵彻角较大时,合成正应力主要是以轴向力产生的正应力的幅值和波形进行传播。
(3)在讨论过程中,仅以比例系数的形式考虑了其它能耗对撞击力的影响,更加合理处理的方式有待进一步的研究。
[1]赵子龙,冯锡敏,邓宏见,等.圆锥杆垂直侵彻半无限厚水泥靶时应力波传播特性研究[J].西安交通大学学报,1998,4(4):59-62.
[2]赵子龙,冯锡敏.圆锥杆侵彻过程及应力波传播分析[J].应用力学学报,2000,17(1):97-101.
[3]徐建波,林俊德,唐润棣,等.长杆射弹侵彻混凝土实验研究[J].爆炸与冲击,2002,22(2):174-178.
[4]王延斌,俞茂宏,林俊德.弹体垂直侵彻混凝土靶体的柱形空腔膨胀理论分析[J].西安交通大学学报,2004,38(3):303-307.
[5]高世桥,刘海鹏,李科杰,等.弹侵彻混凝土靶法向膨胀理论[J].应用数学和力学,2006,27(4):431-438.
[6]赵子龙,张瑾瑾,黄晓琼.长杆弹侵彻半无限厚土的旋转效应分析[J].振动与冲击,2010,29(4):9-11.
[7]李大红,吴强.钨杆弹斜侵彻研究[J].爆炸与冲击,1996,16(2):158-165.
[8]GRAFF KARL F.Wave motion in elastic solids[M].USA:OXFORD UNIVERSITY PRESS,1975.

