6σ稳健设计在单目标优化问题中的仿真应用

周 峰，张学良，贾庭芳，温淑花，吴 量

（太原科技大学机械电子工程学院，太原 030024）

在机械产品设计中，与产品相关的确定性因素和不确定因素常因为时间和环境的变化而发生细微变化，随之影响了产品的质量，降低了产品的可靠性及使用寿命［1］。常规可靠性优化设计应用了概率理论，将影响产品质量的确定性因素和不确定因素处理成不等式概率约束，以此保证其设计要求的可靠度。然而，常规的可靠性优化设计并未能有效地反映出当产品的某些因素在制造和使用的过程中发生变化时，其质量的可靠度也受到了影响。本文在可靠性理论和容差技术的基础上引入6σ稳健设计理论，用以弥补前者的不足之处，在保证要求的可靠度的前提下，使其可靠性对这些因素的微变不十分敏感，提高产品性能的稳健性。

1 6σ的稳健优化设计理念

1.1 6σ稳健设计概念

稳健设计法又称三次设计法［2］，是使设计的产品在制造和使用过程中，当产品结构有关参数发生变化，或者在规定的使用期内其结构发生老化和变质时均能保持产品功能稳定的一种工程设计方法。基于此，摩托罗拉公司为提高产品质量，引入了一种现代质量管理方法——6σ稳健设计［3］。σ即为概率论中的标准差，用以描述结构参数偏离程度。6σ稳健设计结合了可靠性理论和容差模型设计方法，它将产品质量均值的波动限制在6σ范围内，在满足各设计要求的情况下，能使得产品的可靠度达到99.9999998%.实质是在优化过程中，由于结合了可靠性理论和容差设计模型，使得响应均值远离了约束，响应偏差减小。该优化设计方法考虑了随机变量的微变化对目标函数的影响。在优化目标函数的过程中，能够将影响产品质量的相关因素控制在许可的范围内。不同σ水平对应不同的可靠度［4］和每百万件产品缺陷数，见表1.

表1 各σ水平对应的可靠性和每百万件产品缺陷数Tab.1 Sigma level corresponding with the reliability and product defects per million

1.2.1 可靠性概率常规优化设计数学模型

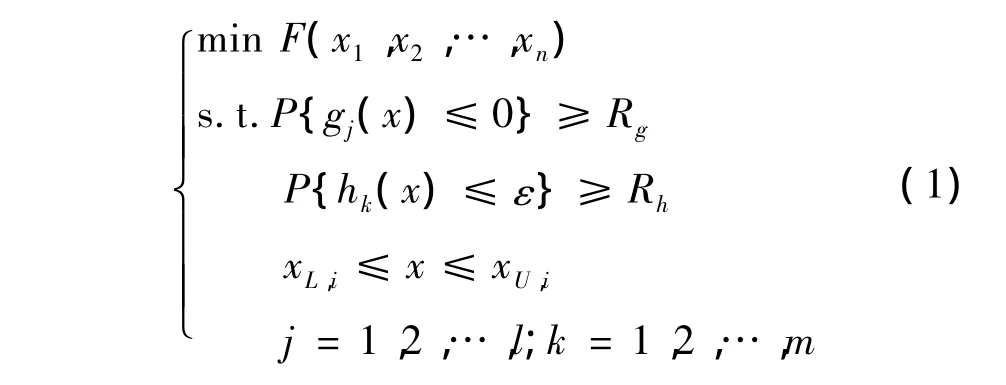
式中:F（x1，x2，x3，…，xn）—— 常规目标函数；

P{·}——约束条件的概率表达；

g（x）——不等式约束函数；

h（x）——等式约束函数；

ε—— 微量，ε ＞ 0；

Rg，Rh——不同约束条件的可靠度；

XL，i，XU，i—— 随机变量 x 的上下限。

1.2.2 6σ稳健优化设计数学模型

式中:m——约束条件数；

n——σ 水平；

w1，w2—— 权因子；

XL，i，XU，i—— 随机变量 xi的上下限；

μxi—— 随机变量 xi的均值；

μy——目标函数y的均值；

μgi——不同约束条件的均值；

σxi——随机变量xi的标准差；

σy——目标函数y的标准差；

σgj——不同约束条件的标准差。

当n=6时，即为6σ稳健设计。与常规确定性优化方法相比，6σ稳健设计的目标函数，加入了目标和约束条件的标准差。该方法不但能寻找到目标函数最优解，而且还使得目标对设计参数变得不敏感。对于各约束，加入约束函数和设计参数的标准差，可使得最优点在搜索的过程中远离约束边界，提升为6σ水平，以有效地增大可靠度，然而，设计参数的可行域也随之而减小范围。因此，要适当扩大设计参数可行域，就有必要在目标函数中加入约束条件的标准差。

1.2.3 均值和方差的近似计算

当确定性因素xi～N（）和不确定性因素～N（）彼此独立时，将设计函数在均值处展开，取二次项可得目标函数或约束函数均值和方差的计算公式［2］:

2 PSO粒子群优化算法

无论何种优化设计模型都必须采用合适的优化算法来获取最佳的参数值以达到模型设计的最初目的。文献［5］表明，如果目标函数和约束条件的非线性程度高些，现有的一些数值优化软件（如MATLAB）很难求得最优解。很多优化设计研究者也都是自行编制适于具体问题的算法来求搜索最优解。因此，本文中将采用粒子群算法来搜索最优解。

粒子群算法［6］按照个体（粒子）的适应度函数的大小进行调整，并利用“群体”和“进化”的概念［7］，让每个粒子在n维搜索空间中以一定的速度飞行，使每个粒子的位置不断发生变化，其飞行速度通过粒子本身飞行过的最好位置和群体中粒子的最好位置进行动态的调整。

设Xi=（xi1xi2…xin）为粒子i的在搜索空间中的位置，Vi=（νi1νi2…νin）为粒子 i的飞行速度，Pi=（pi1pi2…pin）为粒子i曾经的最好适应值位置，即粒子在其飞行历史中的最佳位置。

粒子飞行速度及其空间位置迭代方程可表示为:

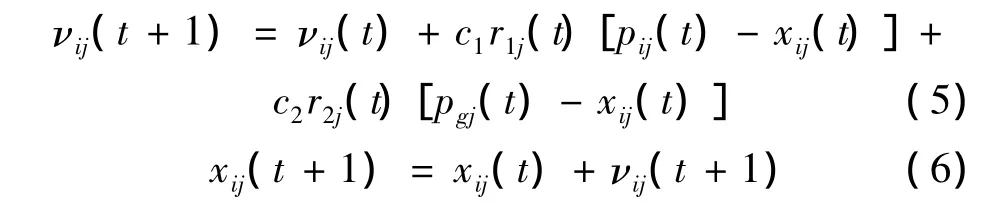
式中，pij（t）为群体的最佳位置。下标“j”表示粒子的第“j”维；“i”表示粒子i；t表示第 t代；c1，c2加速常数，一般取值0 ～ 2，r1～ U（0，1），r2～ U（0，1）为彼此独立的随机函数。

PSO粒子群算法初始化步骤:

（1）给出粒子群的数量N；

（2）在［-xmax，xmax］范围里各粒子依照均匀分布产生对应的粒子位置xij；

（3）在［-νmax，νmax］范围里各粒子依照均匀分布产生对应的粒子飞行速度νij；

（4）对任意 i，设 yi=xi.

算法流程:

（1）根据上述过程，对粒子群的空间位置和飞行速度进行随机的初始化；

（2）计算各粒子的适应函数值的大小；

（3）将各个粒子的适应值与其历史中的最佳位置的适应值做比较。如果较好，即对单目标优化而言，使目标值较小，且符合约束函数，则将该粒子作为当前的最佳位置；

（4）将各粒子的适应值与群体的最佳位置的适应值做比较。同（3），如果较好，则将其作为当前群体的最佳位置；

（5）据式（5），式（6）对粒子的飞行速度和空间位置进行迭代调整；

（6）群体中最佳位置的最优值若没有达到预计中的目标最小值，则返回（2）。

3 实例研究及结果分析

图1 圆柱螺旋压缩弹簧的工作图Fig.1 The working diagram of cylindrical helical compression spring

3.1 算例

设计一圆柱螺旋压缩弹簧［7］（见图1），要求其质量最小。弹簧材料为65 Mn，最大工作载荷Pmax为40 N，最小工作载荷为0 N，载荷变换频率fr为20 Hz，弹簧寿命为104h，弹簧钢丝直径d的取值范围为小于4 mm大于1 mm，中径D的取值范围为小于30 mm大于10 mm，工作圈数n不小于4.5圈，弹簧旋绕比不应小于4，弹簧两端固定。工作温度为50℃，弹簧变形量不小于10 mm.

3.2 常规优化模型的建立

3.2.1 确定设计变量

影响弹簧质量参数有弹簧钢丝直径d，弹簧中径D和弹簧有效圈数n.它们都是彼此独立的参数，故取这三个参数作为设计变量，按连续设计变量处理:

3.2.2 建立目标函数

要优化的单目标是弹簧重量，要求其最小，圆柱螺旋弹簧的重量可表示为:

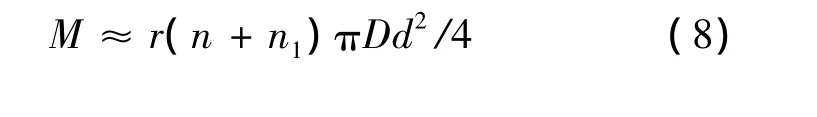
式中，r——弹簧材料密度，对于钢材r=7.8×10-6kg/mm3

n1—— 死圈数，常数 n1=1.5 ～ 2.5，现取 n1=2.

将已知参数代入公式，整理得目标函数为:

3.2.3 约束条件

（1）弹簧的最大切应力发生在弹簧内侧，因此，强度条件约束可表示为:

（2）一般弹簧在确定载荷下会产生一些形变，因此，它需要满足的刚度条件为:

其中，kF——弹簧刚度。

（3）稳定性条件约束［8］

为避免发生失稳现象，可采取控制高径比。对两端固定的弹簧，一般稳定性指标b≤5.3，用公式表示为:

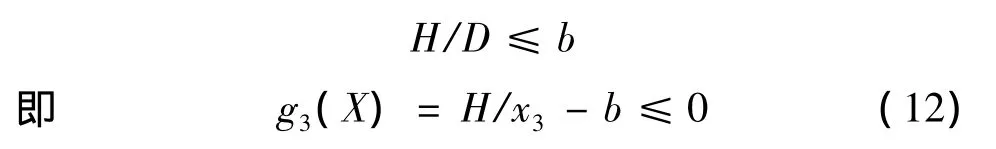
其中，H=540d4/D2+1.5d

（4）两端固定的弹簧不共振条件约束为:

其中，fb—— 自振频率，fb=3.356 × 105d/nD2

（5）弹簧旋绕比C=D/d，故约束条件为:

其中，依据题目取C=4.0.

（6）对 d，n，D 的限制

由dmin≤d≤dmax，nmin≤n≤nmax，Dmin≤D≤Dmax，可得约束条件:

3.3 6σ稳健优化模型的建立

在常规模型的基础上，可以很方便建立6σ稳健优化模型，根据式（7）确定变量如下:

因此，建立稳健优化模型如式（16）所示。其中，w1，w2据实例情况分别取为0.35，0.65.

表2 圆柱螺旋弹簧优化计算结果Tab.2 Experimental results of cylindrical helical spring optimization

3.4 优化方法及结果分析

根据建立的优化设计数学模型及6σ稳健优化设计数学模型，采用粒子群智能优化方法进行寻优，并利用Isight集成MATLAB平台进行可靠度分析。表2给出了常规优化方法和6σ稳健优化设计方法的对比。

4 结论

6σ稳健优化设计是融合了可靠性理论和基于容差模型的稳健设计理论，充分考虑了有关产品的确定性和不确定因素对产品性能的影响，将设计提高到了6σ水平，使其可靠度达到了近100%，提升了产品性能在这些因素发生变化时的不敏感性。将该方法应用于圆柱螺旋弹簧的优化设计中得到了很好的设计结果。与常规优化方法结果相比，弹簧的可靠性和稳健性都得到了较大的提高。

［1］张义民，贺向东，刘巧伶，等.任意分布参数的机械零件的可靠性稳健设计（一）:理论部分［J］.工程设计学报，2004，11（5）:233-237.

［2］陈立周.稳健设计［M］.北京:机械工业出版社，2000.

［3］李玉强，崔振山，阮雪榆，等.6σ概率设计优化方法及其应用［J］.中国工程机械，2004，15（21）:1916-1919.

［4］P N KOCH，R J YANG，L GU.Design for six sigma through robust Optimization［J］.Struct Multidisc Optim，2004，26（10）:235-248.

［5］COLOMI A，DORIGO M，MANIEZZO V.Distributed optimization by ant colonies［C］//Proc 1st European Conf Artificial Life Plans，France:Elsevier，1991:134-142.

［6］彭喜元，彭宇，戴毓丰.群智能理论及应用［J］.电子学报，2003，31（12）:1982-1988.

［7］苏金明，阮沈勇.MATLAB实用教程［M］.2版.北京:电子工业出版社，2008.

［8］濮良贵，纪名刚.机械设计［M］.7版.北京:高等教育出版社，2005.