基于去趋势波动分析和支持向量机的癫痫脑电分类

蔡冬梅， 周卫东， 李淑芳， 王纪文， 贾桂娟， 刘学伍

1．山东大学信息科学与工程学院，济南 250100；

2．山东大学齐鲁医院，济南 250012

基于去趋势波动分析和支持向量机的癫痫脑电分类

蔡冬梅1， 周卫东1， 李淑芳1， 王纪文2， 贾桂娟2， 刘学伍2

1．山东大学信息科学与工程学院，济南 250100；

2．山东大学齐鲁医院，济南 250012

癫痫脑电的自动检测与分类对于癫痫患者的诊断治疗具有重要意义。本文提出了一种基于去趋势波动分析(detrended fluctuation analysis,DFA)、波动指数和支持向量机(support vector machine,SVM)的癫痫脑电分类方法。首先采用DFA方法计算脑电的标度指数，然后对脑电进行4～8 Hz、8～13 Hz、13～30 Hz带通滤波并分别计算波动指数，最后使用SVM分类器实现癫痫脑电波的自动分类。对临床脑电信号的实验表明，该方法具有较强的检测性能，分类准确率达到97%。

脑电图；去趋势波动分析；癫痫检测；支持向量机；波动指数

引 言

癫痫是常见的慢性脑部疾病，其发作是因为大脑神经元过度同步化放电引起的突然而短暂的脑功能失调，引起运动、感觉、意识等多种不同的障碍和脑细胞的死亡。癫痫脑电图对病灶的定位和病情分析都有重要意义。由于癫痫发作的不确定性，脑电图需要长时间记录，为此脑电图阅读对医务工作者是一项复杂并且耗时的工作。因此，脑电的自动检测与分类就越发显得迫切与重要。

从20世纪60年代起，癫痫EEG的自动检测技术就受到注意，很多学者在这一领域做了大量的研究[1～7]，提出了多种自动检测方法。根据癫痫脑电和正常脑电的不同特点，对于脑电图特征的提取也提出了很多种方法。其中一类方法主要是利用癫痫波波形的时频特征，其本质是试图量化人的视觉评估过程，这类特征有：1)模板匹配[1]，将检出的波形与癫痫脑电模板进行病发识别；2)拟态法特征 (mimetic)[2]，提取波形的相关参数进行识别，比如，一阶导数、二阶导数、曲率和微分等特征；3)相对能量[3]，计算癫痫经常出现的频段的能量在脑电各频段能量和中所占的比例；4)相对振幅[3]，利用癫痫发作时的振幅比发作前背景的振幅大这一特性作为分类特征。另一类方法是基于癫痫发作时脑电信号的复杂度降低、混沌性减弱这一特性，采用脑电的非线性动力学特性作为分类特征，这类特征有：1)近似熵和样本熵[4]，利用癫痫发作时脑电混沌性减少、变得简单这一特性作为分类特征；2)Hurst指数[5]，是利用癫痫脑电图的长程相关性小于正常脑电波的特点来作为分类特征；3)Lyapunov指数[6]，即基于混沌系统对初始条件的敏感依赖性作为分类特征的；4)关联维数[7]，是根据癫痫脑电较正常脑电关联维数会降低作为分类特征的。由于脑电信号具有非稳态和非线性特性，近年来非线性分析方法成为研究的热点，以期揭示大脑神经元活动所具有的非线性动力学特征。在癫痫检测的过程中，为保证系统具有较高的正确率、较低的漏检率和误检率，常常把多种特征和方法综合使用，以提高系统的性能。

1994年，Peng等人提出了去趋势波动分析 (detrended fluctuation analysis,DFA)方法，并用该方法检测DNA内部分子链的相关性程度[8]。通常的非线性方法，比如计算相关维数和Lyapunov指数，都要求平稳或准平稳的条件，但对于生物信号来说几乎不可能满足。DFA适用于研究各种非稳态时间序列的长程幂律相关性。近年来，该方法已被应用于生命科学、气象学、地质学、经济学等多个领域，成为检测非平稳时间序列的有效工具。

本文提出了一种新的基于去趋势波动分析方法和支持向量机 (support vector machine,SVM)的癫痫脑电分类算法。首先对脑电数据采用DFA方法计算标度指数 (scaling exponent)α，判断脑电数据的相关性，然后对脑电数据进行滤波以突出相应频带的特征，同时抑制伪差信号的干扰，再计算相应频段内波幅的波动指数体现脑电信号波动大小的变化，最后将标度指数α和波动指数输入SVM分类器以实现癫痫波的自动分类。在对临床脑电数据的实验中，该算法取得了较理想的检测率和误检率。

去趋势波动分析和支持向量机

去趋势波动分析

去趋势波动分析法 (DFA)是一种标度分析方法，用于定量分析非平稳时间序列的长程相关性，或称长程幂律相关性[8]。DFA首先滤除信号本身演化的趋势成分，然后对剩下的波动成分进行分析，以减少由于不完善的测量方法等引起的噪声。Peng等人[9]已成功运用DFA分析了心律变异非平稳时间序列的相关性。

DFA的计算过程分为以下步骤[8,9]：

1)一段长度为N的有限长脑电时间序列s(i)，能够被构造成一个去均值的和序列z(j)。

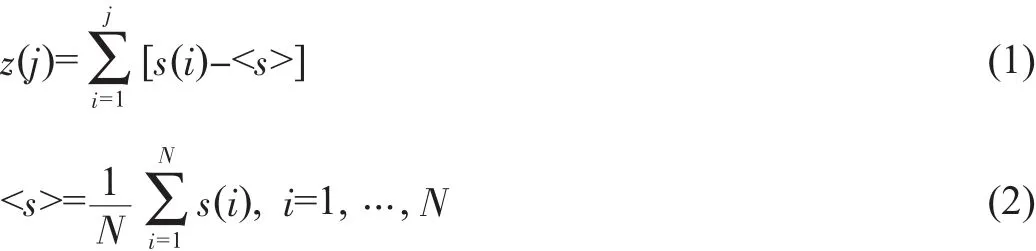
2)将新序列z(j)不重叠地分解成若干长度为n的等长片段，因此z(j)被分成K=int(N/n)个片段，每段记为zk(k=1,…,K)。

3)计算每一个zk(k=1,…,K)的线性趋势，记为k=1,…,K)。

4)计算均方误差：

6)n每增加一个单位，重复步骤2)～5)。则存在幂律形式的波动：

其中α即为标度指数。

7)画出纵坐标为log[E(n)]，横坐标为log(n)的曲线，则曲线的斜率即为这段时间序列的标度指数α。

标度指数α是判定序列长程幂律相关性的一个重要指标，当α=0.5时，时间序列中不存在任何相关，即时间序列是随机的；当α≠1/2时，时间序列存在长程幂律相关；当0＜α＜0.5时，时间序列具有反持续性，反持续性行为的强度随α的减小而增强；当0.5＜α＜1时，时间序列具有持续性，持续性行为的强度随α的增大而增强。

脑电波动指数

当癫痫发作时，大脑会产生尖波、棘波、慢波、尖慢综合波、棘慢综合波等脑电波形，癫痫发作脑电信号的波动会比未发作的间歇期剧烈，为此，定义如下波动指数来衡量信号v变化的强度：

5)计算均方误差的平均值：

其中，m为信号的长度。

支持向量机

支持向量机 (SVM)是根据统计学习理论提出的一种新的机器学习方法，具有很好的推广性。与现有的其他学习机器相比，SVM建立在坚实的理论基础上。其基本思想是，对于线性不可分样本，经非线性变换将其映射到另一个高维空间中，在变换后的空间中寻找一个最优的分界面 (超平面)，使之线性可分[10,11]。

假设存在一个最优超平面将特征空间分为两个区域，已知大小为l的训练样本集(x1,y1),…(xl,yl),xi∈Rn,yi∈{-1,+1}表示类别号，如果xi在超平面的正侧，则yi=+1；若在超平面的负侧，则yi=-1。学习的目标就是构造一个判别函数，即找到一个分类面，将待测数据尽可能正确地分开。若超平面：

满足：1)对所有样本分类正确，即yi[(w·xi)+b]-1≥0,i=1,2,…,n；

2)分类间隔最大，即‖w‖最小。

其中，w·x表示向量w与向量x的内积，则该超平面为最优超平面，利用Lagrange优化方法，可以把上述求最优分类面问题转化为求其对偶问题：

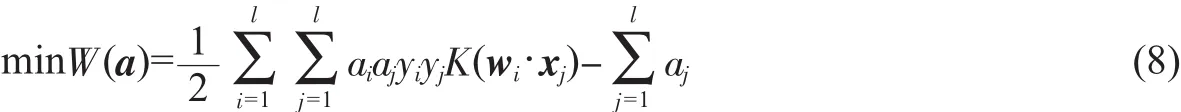
满足的约束条件为

上式中，C是惩罚因子，即综合考虑最少错分样本和最大分类间隔，K(x,xi)为满足Mercer条件的核函数。求解支持向量的本质是式(8)在约束条件下的二次函数寻优问题，求解后可得最优判别函数：

其中ai*为支持向量系数，b*为分类阈值，m为支持向量的个数。其中，核函数的形式主要有三种：多项式核函数、径向基函数、Sigmoid函数[12]。本文选择径向基核函数，即：σ为函数的宽度参数。

癫痫脑电分类方法

本算法采用DFA方法计算脑电信号的标度指数α和特定频段脑电信号的波动指数作为检测特征，将其输入到SVM分类器中，实现癫痫脑电波的自动分类。具体流程见图1。

图1 癫痫脑电分类算法流程图Fig.1 Flow chart of EEG classification algorithm

计算标度指数α

采用去趋势波动分析的方法计算癫痫脑电和发作间期脑电信号的标度指数α，作为SVM分类器的输入特征。其中窗口n的取值范围是从最小32开始，然后是32的倍数，一直到整个时间序列的长度1024。

计算波动指数

癫痫脑电波一般出现在3～30 Hz，为突出此频段内信号特征的变化以及去除伪差干扰的影响[13]，在计算波动指数之前对EEG进行滤波。本文设计了三个切比雪夫Ⅱ型带通数字滤波器，为减少滤波器造成的相位失真，采用零相位数字滤波[14]，取三个频段4～8 Hz、8～13 Hz和13～30 Hz对脑电信号进行滤波，分别对应脑电的α波、β波和θ波。

癫痫发作一般表现为变化剧烈的高波幅的电活动，因此波幅的波动指数可作为检测癫痫发作的重要依据。对滤波后数据求波动指数，作为其特征。

脑电分类

将标度指数α和波动指数输入到SVM分类器进行训练，获得其最优参数。然后使用测试数据验证基于DFA、波动指数和SVM的癫痫检测算法的性能。

实验及结果

本实验使用Intel core2 2.00GHz处理器，运行平台为Matlab 7.0。实验数据采用山东大学附属齐鲁医院的6位儿童病人的临床脑电数据，采样频率为128 Hz。训练样本中，间歇期和发作期均为256段，每段1024点。测试样本中，间歇期和发作期也均为256段，每段1024点。用作训练的间歇期脑电和癫痫脑电的标度指数α分布图及其盒形图见图2，癫痫发作期和间歇期脑电的标度指数平均值分别为0.16和0.44。由图中可见，癫痫间歇期脑电的α值大于发作期。

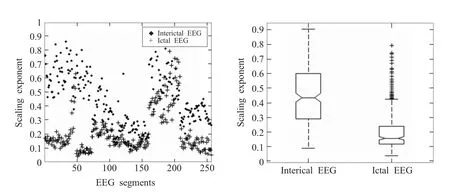
图2 间歇期脑电和癫痫脑电的标度指数α分布(A)及其盒形图(B)Fig.2 Scaling exponent distribution(A)and its box-plot(B)of interictal EEGs and ictal EEGs

间歇期脑电和癫痫脑电的波动指数的盒形图如图3所示，从图中可以看出，癫痫发作期间脑电的波动指数大于间歇期，两者有明显的区分。

在试验中，先单独使用脑电的标度指数α作为特征进行癫痫脑电分类。使用DFA标度指数α训练得到SVM最优参数 (最优参数σ=2，C=256)，并通过测试数据检验算法的分类性能，测试结果表明：256段癫痫脑电数据有69段没有被检测出来，另外256段间歇期脑电数据有56段被误判为癫痫，总体识别率为74%。

图3 间歇期脑电和癫痫脑电三层滤波后的波动指数盒形图 (A)4～8 Hz带通滤波后的波动指数；(B)8～13 Hz带通滤波后的波动指数；(C)13～30 Hz带通滤波后的波动指数Fig.3 Box-plots of fluctuation indices of interictal EEG and ictal EEG after filtered by three level filters (A)4～8 Hz fluctuation indices;(B)8～13 Hz fluctuation indices;(C)13～30 Hz fluctuation indices

然后单独使用脑电的波动指数作为特征进行癫痫脑电分类。使用波动指数训练得到SVM最优参数 (最优参数σ=8，C=512)，并通过测试数据检验算法的分类性能，测试结果表明：256段癫痫脑电数据有19段没有被检测出来，另外256段间歇期脑电数据有0段被误判为癫痫，总体识别率为96.3%。

采用非线性和线性特征相结合的方法，将训练数据的加权标度指数α和波动指数一起，作为特征输入SVM分类器，调整参数获得最优检测能力 (最优参数σ=8，C=1024)，然后使用测试数据测试算法的性能。实验结果表明：256段癫痫脑电数据有11段没有被检测出来，另外256段间歇期脑电数据有4段被误判为癫痫，总体识别率达到97.1%。三种方法的分类检测结果见表1。

表1 脑电分类实验结果Table 1 Experimental results of EEG classification

表2给出AR模型+神经网络常规脑电分类方法的试验结果与本文方法的对比。利用Burg算法对脑电数据建立6阶AR模型，并将所得AR模型的系数作为检测特征；利用学习率可变的动量BP算法训练神经网络，隐层节点个数取为30；然后用测试样本检测神经网络的分类性能。本文提出的DFA+波动指数+SVM方法的准确率优于AR模型+神经网络方法。

表2 本文方法与AR模型+神经网络方法结果比较Table 2 Comparison of our approach with AR model+Neural network approach

讨 论

由于人脑是复杂的非线性动力学系统，鉴于DFA可衡量时间序列的统计相关性，能够良好地刻画出脑电序列的非线性行为特征。本文实验结果表明，癫痫期间脑电的标度指数平均值为0.16，间歇期脑电的标度指数平均值为0.44。因此脑电的α值在癫痫发作间期和发作期存在较大差异，癫痫脑电具有更强的反持续相关性。这和癫痫的生理特点是相吻合的，癫痫发作期间，脑电混沌性减弱，脑电波更易改变，反持续相关性增强；而在未发作时，脑电较为复杂，相关性较弱，更加接近白噪声 (白噪声的α=0.5)。

癫痫是以大脑猝发性同步放电为特征的，癫痫发作时，脑电信号波动剧烈，波动指数会明显增大。本文将DFA标度指数和波动指数相结合构成脑电的分类特征，并采用SVM分类器进行分类。首先使用DFA方法计算标度指数α来确定脑电信号的非线性特性；然后对脑电滤波，突出相应频带的特征变化并抑制伪差信号的干扰，再计算相应频段内的波动指数；最后将α和波动指数输入SVM分类器实现癫痫波的自动检测和分类。采用DFA和波动指数分别从非线性和线性两个角度提取脑电信号的特征，两者的结合提高了癫痫脑电分类的性能。

1. SankarR, NatourJ. Automaticcomputeranalysisof transients in EEG.Comput Biol Med,1992,22(6):407～422

2.PradhanN,DuttDN,Satyam SS. A mimetic-based frequency domain technique for automatic generation of EEG reports.Comput Biol Med,1993,23(1):15～20

3.Sukhi G,Gotman J.An automatic warning system for epilepticseizuresrecorded on intracerebralEEGs. Clin Neurophysiol,2005,116(10):2460～2472

4. Srinivasan V, Eswaran C, Sriraam N. Approximate entropy-based epileptic EEG detection using artificial neural networks.IEEE Trans Inform Technol Biomed Engin,2007,11(3):288～295

5.Nurujjaman M,Ramesh N,Sekar Iyengar AN.Comparative study of nonlinear properties of EEG signals of normal persons and epileptic patients.Nonlin Biomed Phys,2009,3(1):6

6. Swiderski B,Osowski S,Rysz A.Lyapunov exponent of EEG signal for epileptic seizure characterization.Chaos,1995,5(1):82-～87

7. 王兴元，孟娟，邱天爽.基于独立分量分析算法研究儿童癫痫脑电的混沌动力学特征.生物医学工程学杂志，2007,24(4):835～841 Wang XY,Meng J,Qiu TS.Research on chaotic behavior ofepilepsyelectroencephalogram ofchildren based on independentcomponentanalysis algorithm. J Biomed Engin,2007,24(4):835～841

8.Peng CK,Buldyrev SV,Havlin S,Simons M,Stanley HE,Goldberger AL.Mosaic organization of DNA nucleotides.Phys Rev,1994,49(2):1685～1689

9. Peng CK, Havlin S, StanleyHE, GoldbergerAL.Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series.Chaos,1995,5(1):82～87

10.Mauro S,Mauro S. Automatic recognition of epileptic seizure in EEG via support vector machine and dimension fractal. Proceedings of the 2009 international joint conferenceon NeuralNetworks. Atlanta USA, 2009.3321～3325

11.Guler I,Ubeyli ED.Multiclass support vector machines for EEG-signals classification. IEEE Trans Inform Technol Biomed,2007,11(2):117～126

12.边肇祺,张学工.模式识别 (第二版).北京:清华大学出版社,2000 Bian ZQ,Zhang XG.Pattern Recognition(Second Edition).Beijing:Tsinghua University Press,2000

13.Khan YU,Gotman J.Wavelet based automatic seizure detection in intracerebral electroencephalogram. Clin Neurophysiol,2003,114(5):898～908

14.纪跃波,秦树人,汤宝平.零相位数字滤波器.重庆大学学报(自然科学版),2000,23(6):4～7 Ji YB,Qin SR,Tang BP.Digital filtering with zero phase error.J Chongqing Univ(Natl Sci Ed),2000,23(6):4～7

15.宁艳,江朝辉,安滨,冯焕清.睡眠生理参数的去趋势波动分析.生物医学工程学杂志,2007,24(2):249～252 Ning Y,Jiang CH,An B,Feng HQ.Detrended fluctuation analysisofphysiologicalparameters. JBiomed Engin,2007,24(2):249～252

16.刘晓霞.临床脑电图学.北京:人民卫生出版社,2005 Liu XX.Clinical EEG study.Beijing:People's Medical Publishing House,2005

Classification of Epileptic EEG Based on Detrended Fluctuation Analysis and Support Vector Machine

CAI Dongmei1,ZHOU Weidong1,LI Shufang1,WANG Jiwen2,JIA Guijuan2,LIU Xuewu2
1.School of Information Science and Engineering,Shandong University,Jinan 250100,China;
2.Qilu Hospital,Shandong University,Jinan 250100,China

This work was supported by grants from The National Natural Science Foundation of China(30870666),The Program of Development of Science and Technology of Shandong(2010GSF10243)and The Independent Innovation Foundation of Shandong University(2009JC004)

Oct 7,2010 Accepted:Nov 16,2010

ZHOU Weidong,Tel:+86(531)86333629,E-mail:wdzhou@sdu.edu.cn

The automatic seizure detection in electroencephalogram (EEG) is significant for diagnosing epilepsy.This paper proposes a new seizure classification approach based on detrended fluctuation analysis(DFA),fluctuation index and support vector machine(SVM).Firstly,the scaling exponents were calculated as features for epileptic EEG.EEG was then filtered by 4～8 Hz,8～13 Hz and 13～30 Hz band-pass filters and fluctuation indiced within different frequency bands were calculated.Lastly,a SVM classifier was used to classify seizure automatically.The experimental results show that the proposed classification algorithm is accurate and efficient with a recognition rate of 97%.

Electroencephalogram; Detrendedfluctuationanalysis; Seizuredetection; Supportvector machine;Fluctuation index

2010-10-07；接受日期：2010-11-16

国家自然科学基金项目(30870666)，山东省攻关计划项目(2010GSF10243)，山东大学自主创新基金资助课题(2009JC004)

周卫东，电话：(0531)86333629，E-mail：wdzhou@sdu.edu.cn

TP202+.3