循环荷载下半圆堤整体稳定性计算方法研究
周宝勇,王元战,余建星
(天津大学建筑工程学院港口与海洋工程教育部、天津市重点实验室,天津 300072)
循环荷载下半圆堤整体稳定性计算方法研究
周宝勇,王元战,余建星
(天津大学建筑工程学院港口与海洋工程教育部、天津市重点实验室,天津 300072)
针对圆弧滑动面法已无法准确判断土体强度发生弱化后半圆堤整体稳定性问题,建立基于循环强度结合D-P屈服准则的拟静力有限元模型来分析半圆堤整体稳定性。分析荷载破坏包络线的变化趋势,给出提高半圆堤整体稳定性的工程建议。并在有限元数值分析结果基础上,对变量进行无量纲化,通过优化分析进行非线性拟合归一得出描述半圆堤整体稳定性的极限状态方程。以长江口深水航道治理二期工程为例,结果表明简化计算方法是可靠的,可供工程设计借鉴和使用。
半圆堤;整体稳定性;强度弱化;破坏包络线;循环荷载
Abstract:The traditional circular slidingmethod is not able to calculate the integral stability of semi-circular breakwater structure with soil strengthweakening.Pseudo-static FEmodel based on the conceptof cyclic strength and considering D-P yield criterion is established.Engineering advices are proposed to improve the integral stability of semi-circular breakwater by analyzing the trend of failure envelope.Based on the FE numerical results,a limit state equation is proposed by using dimensionless variable technique and Optimizing Analysis Software.The Yangtze estuary deepwater channel regulation phase IIproject is taken as the example,and the results show that the simplified calculation method is reliable and can be used in engineering design.
Key words:semi-circular breakwater;integral stability;strengthweakening;failure envelope;cyclic loading
半圆堤由预制的半圆型拱圈和底板组成,放置于基床上,在天津港及长江口深水航道治理工程中被广泛采用。但由于半圆堤自身结构较轻,在波浪荷载作用下整体结构极有可能发生失稳破坏,包括滑移破坏、倾覆破坏和地基整体失稳。2002年长江口深水航道治理二期工程半圆堤结构发生不同程度的沉陷,损坏的主要原因[1]是波浪循环荷载作用下土体强度发生弱化,最终导致结构发生失稳。港口工程地基规范[2]对于地基稳定性的验算采用圆弧滑动面法,但此法没有考虑土体的本构关系,而且在土体强度发生弱化后未能准确描述地基稳定性的影响。
考虑由循环荷载作用引起土体强度发生弱化,准确合理进行半圆堤整体稳定性分析是亟待解决的问题。通过在ABAQUS上进行二次开发将循环强度与D-P屈服准则相结合来考虑土体弱化,建立分析半圆堤整体稳定性的拟静力有限元模型,并在数值分析的基础上通过优化拟合给出了计算半圆堤整体稳定性的简化方法。
1 有限元分析方法
1.1 循环承载力模型
由Andersen[3]给出的循环强度定义可知,土体的循环强度与静剪应力σs和循环剪应力σd组合有关,见式(1),其物理含义:在一定循环次数下,土单元达到变形破坏标准时,作用在其上的静应力和循环应力之和。

式中:σd,f为土体循环剪切强度;σs为静应力;σd为动应力。
根据D-P屈服准则,屈服强度:

式中:p为静水压力,β为D-P模型内摩擦角,c为D-P模型中材料的黏聚力。将D-P屈服准则与循环强度概念相结合,得:

式(3)即为基于D-P屈服准则和三轴试验建立的循环强度模型。循环破坏次数取N=1 000次,即按一般波浪的平均周期为10 s左右计算,1 000次约为3 h,相当于防波堤遭受一次典型的风浪作用时间。当软黏土内摩擦角为零时,D-P屈服准则即退化为Mises屈服准则。
1.2 有限元模型
由于半圆堤的长度尺寸远大于其断面尺寸,将其简化成平面应变问题来考虑。为减小地基边界效应对数值计算精度的影响,地基侧向宽度取为20B(B为基础宽度),深度取为10B,在ABAQUS上建立有限元模型,其中采用二阶减缩积分单元(CPE8R),通过对子程序USDFLD的开发实现循环承载力模型。
目前的二维复合加载方式主要有Swipe加载和荷载-位移控制搜寻法两种。考虑到荷载-位移控制搜寻方法的计算精度较高且半圆堤平面应变模型计算量较小,采用荷载-位移控制进行加载。荷载-位移控制搜寻方法主要包含两个步骤:
1)通过荷载控制直接施加已知荷载分量,为破坏包络线内相应的一点;
2)保持所施加的荷载不变,沿另外方向施加位移直到相应荷载值不再随位移增加而变化,由此可确定出破坏包络线上的一个点。
半圆堤地基循环极限承载力的计算步骤[4]:
1)以土的静强度为破坏标准,根据作用在结构上的静荷载确定土单元的等效静应力σs;
2)根据计算得到的各个土单元的静应力σs,确定地基中各个土单元的循环强度;
3)以土单元的循环强度为破坏标准,计算静荷载与循环荷载共同作用下荷载位移曲线(P-S曲线);
4)根据有限元计算出的P-S曲线,判断半圆堤整体是否已发生失稳,确定地基循环承载力。
2 有限元数值结果分析
为了确保求解精度与获得良好的收敛速度,根据文献[5]的建议,不排水饱和软黏土地基的E/c取值范围为200~500,在此取计算比值300,粘性土地基中E/c的取值范围为2 000~5 000,计算时E/c取为4 000。影响半圆堤整体稳定性的因素主要包括土体重度γ、基床底宽B、土体黏聚力c、土体内摩擦角φ。考虑到半圆堤结构常放置于明基床上的特点,所以在这并未考虑基础有埋深的情况。
假定基底完全粘结,即认为半圆堤结构不会发生滑移和倾覆破坏,而当承受较大荷载时整体结构将产生失稳破坏。这与实际情况可能先发生滑移破坏不符合,所以在实际工程运用时,需将给出的荷载破坏包络线结合防波堤设计与施工规范[6]关于抗滑抗倾的规定,从而全方位的保证半圆堤结构设计的可靠性与安全性。
2.1 荷载破坏包络线分析
2.1.1 纯黏土基础
纯黏土(φ=0)基础上半圆堤在不同土体重度γ、基床底宽B和土体黏聚力c的荷载破坏包络线(未考虑土体弱化效应)如图1~图3所示。
从图1至图3中可以看出基底宽度、土体重度及黏聚力在经过归一处理后对纯黏土上荷载破坏包络线基本不产生影响,归一性很好。另外,当竖向静荷载Vs与竖向承载力Vu的比值小于0.5时,水平静极限承载力H基本不变;当Vs/Vu大于0.5时,水平极限承载力以较大的幅度减小。
将有限元计算的纯黏土基础上半圆堤荷载破坏包络线与已有近似解[7-8]进行对比(未考虑土体弱化效应),结果如图4所示。从图4中可以看出,有限元结果与 Green解和Bolton解基本稳合,因此也可考虑用Green解和Bolton解来近似描述纯黏土基础上半圆堤的荷载破坏包络线。另外也说明了采用有限元模型计算出的荷载破坏包络线是准确的。
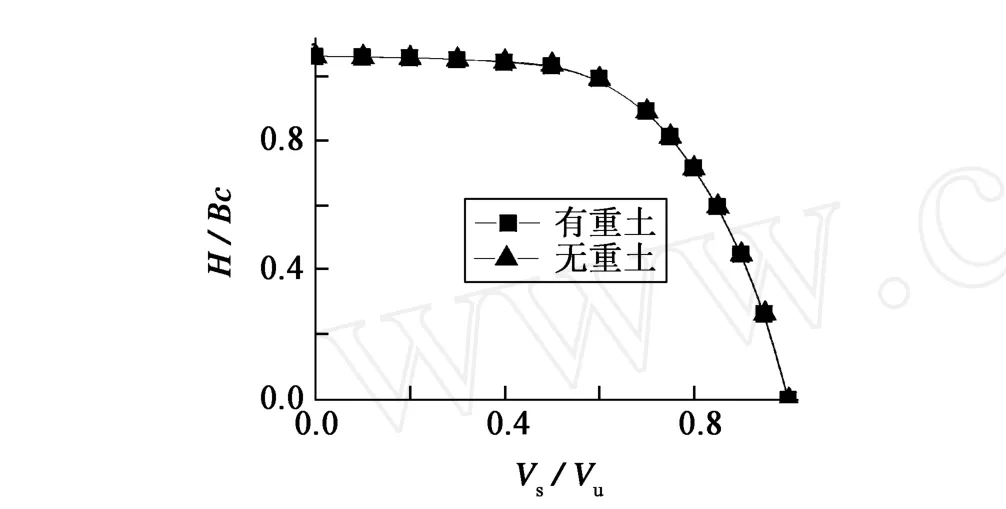
图1 土体重度γ对半圆堤荷载破坏包络线的影响Fig.1 The effectof gravity on failure envelope

图2 基底宽度B对半圆堤荷载破坏包络线的影响Fig.2 The effectof breadth of strip-base on failure envelope

图3 土体黏聚力c对半圆堤荷载破坏包络线的影响Fig.3 The effectof cohesive force on failure envelope
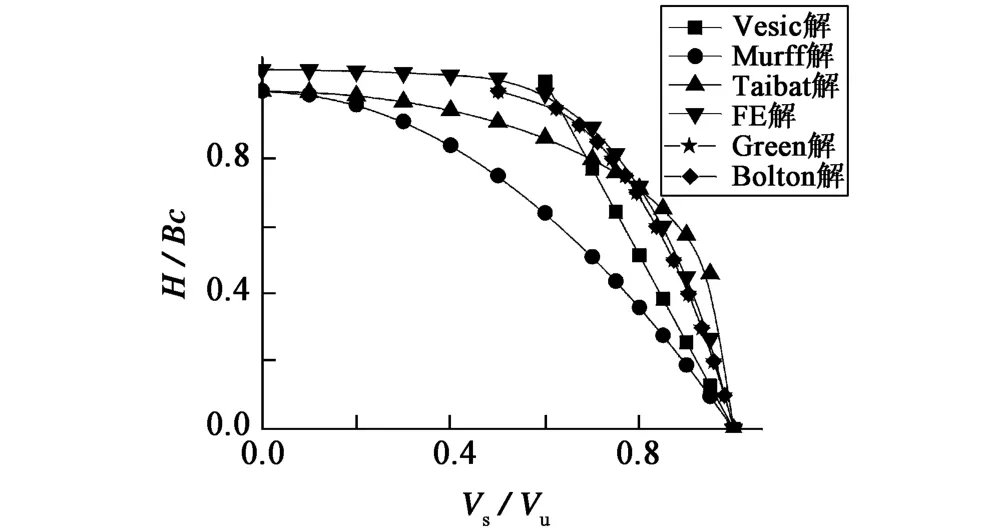
图4 有限元解与其他近似解的对比Fig.4 The comparisonof FE solutionswithother approximate solutions
在循环荷载作用下,土体强度会产生弱化效应,采用基于循环强度结合Mises屈服准则的拟静力法建立有限元模型。以结构参数B=20 m,c=15 kPa,φ=0,γ=7.5 kN/m3为例,图5中给出了该组参数下半圆堤在循环荷载作用下土体强度发生弱化和不发生弱化时的荷载破坏包络线对比图。
从图5中可以看出,土体强度弱化对于结构水平动承载力Hd的影响是比较明显的,在工程设计时是不能忽略的。随着半圆堤结构静自重的增加,循环承载力的弱化值逐渐减小,这与循环强度与静剪应力之间关系式的变化是相符的,即静剪应力较小时,循环强度较小,静剪应力较大时,循环强度也跟着增大。
2.1.2 普通黏性土基础
采用循环强度结合D-P屈服准则来计算普通黏性土(φ≠0)基础上结构的循环承载力。以土体内摩擦角φ=5°和φ=10°为例,分析普通黏性土基础上荷载破坏包络线的变化情况,如图6所示。
从图6中可以看出,对于普通粘性土,半圆堤荷载破坏包络线受土体内摩擦角的影响较大,随着土体内摩擦角的增大,荷载破坏包络线呈非线性增长趋势。由于D-P屈服准则与静水压力有关,随着竖向静荷载Vj的增大,静水压力增大,导致土体循环强度下降得很小。当φ=5°时,竖向静荷载比达到0.4时,土体产生弱化效果就基本可以忽略了,且这个临界值随着内摩擦角的进一步增大而降低;当φ=10°时,临界值接近0.3。

图5 土体(φ=0)强度弱化对半圆堤荷载破坏包络线的影响Fig.5 The effectof the strength weakening of soil(φ=0)on failure envelope

图6 土体(φ=5°和10°)强度弱化对半圆堤的荷载破坏包络线的影响Fig.6 The effect of the strength weakening of soil(φ=5°and 10°)on failure envelope
2.2 工程设计建议
根据对荷载破坏包络线变化趋势的分析可知,在对半圆堤整体稳定性进行工程设计时,为增强整体稳定性可采取以下措施:
1)在工程设计时仅对半圆堤结构进行抗滑抗倾覆验算是不能完全保证整体结构的安全性,还必须结合整体稳定性破坏包络线进行整体稳定性验算,以充分保证整体结构的安全可靠。
2)在保证竖向承载力满足相应安全余度且波浪荷载较大时,可适当增大竖向静荷载的值,因为在一定范围内水平极限承载力随着竖向静荷载比的增大而增大,计算结果显示该临界值介于(0.4,0.5)Vu之间。具体工程措施如提高半圆堤自身构件重量或者增加填砂重量等。
3)对地基进行加固以提高土体的黏聚力及内摩擦角,而其中内摩擦角的增大对水平承载力的贡献更大。具体工程措施,如堆载预压或打塑料排水板等。
3 简化计算方法
基于循环强度的有限元计算模型比较复杂,对工程结构设计人员的要求较高,不利于工程上的展开和运用。为寻求一种简化判断循环荷载作用下半圆堤整体稳定性的方法,通过计算出不同结构参数的半圆堤整体临界失稳情况,进而对大量数据结果进行非线性拟合归一。
对各变量进行无量纲化,以无量纲形式对极限状态方程进行拟合。具体处理形式如下,水平极限承载力Hs/Bc;竖向极限承载力Vs/Bc;竖向静荷载Vs/Vu;内摩擦角tanφ。根据荷载破坏包络线随各影响因素的变化趋势,结合优化分析软件1stOpt,基于麦夸特法(levenberg-marquardt)和通用全局优化法求解半圆堤整体稳定性的极限状态方程。
3.1 不考虑土体强度弱化下半圆堤整体稳定性的极限状态方程
纯黏土(φ=0)基础上半圆堤整体稳定性的极限状态方程:

式中:H′为纯黏土基础上半圆堤水平静极限承载力;Vs为竖向静荷载;Vu为竖向极限承载力;B为基底宽度 ;c为土体黏聚力 ;εv=Vs/Vu;α=1.063;β=5.02;χ=0.96。
普通黏性土(φ≠0)基础上半圆堤整体稳定性的极限状态方程:
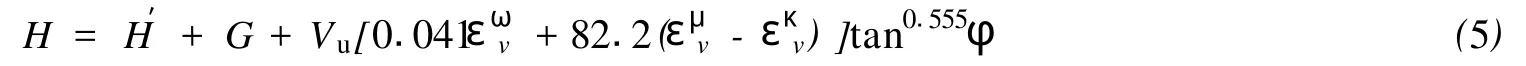
式中:H为普通黏性土基础上半圆堤水平静极限承载力;φ为土体内摩擦角;μ=1.498+40.59tan8.75φ;G=0.479Bctan0.69φ;κ=1.506+20tan7.75φ;ω=12.647;其他符号同前 。
3.2 考虑土体强度弱化下半圆堤整体稳定性的极限状态方程
由于循环强度与土体静剪应力比有关,很难进行极限状态方程的归一。定义水平承载力弱化强度:

式中:λ为水平承载力弱化强度;Hd为水平循环承载力;Hs为水平静承载力。
纯黏土(φ=0)基础上的水平承载力弱化强度:

式中:λs为循环荷载作用下纯黏土基础上半圆堤水平承载力弱化强度;其他符号同前。
普通黏性土(φ≠0)基础上的水平承载力弱化强度:

式中:λ为循环荷载作用下普通黏性土基础上半圆堤水平承载力弱化强度;其他符号同前。
4 工程实例
以长江口深水航道治理二期工程中的三个典型半圆堤[9]断面为例,三个典型断面中有破坏较为严重的,有轻微下沉的,有基本稳定的。北导堤NIIA标段即典型断面I为稳定情况,南导堤SIIB标段即典型断面II为临界情况,而北导堤NIIB标段即典型断面III为破坏状态。半圆堤结构特征如图7所示,三个典型断面的基本特征如表1所示。水位取设计高水位4.02 m(吴淞基面),断面 I、II、III的波高H1%分别取5.14、6.40、7.12m;周期T分别为 7.76、8.53、7.76 s。

图7 半圆堤结构特征Fig.7 The section of semi-circular breakwater
根据式(5)和(8)进行计算,其中土层参数按规范[1]关于分层土体参数的取法进行选取计算,半圆堤所受的总水平波浪力根据文献[10]的经验公式进行计算。半圆堤整体稳定分析的计算结果如表2所示。

表1 三个典型断面的特征Tab.1 The characteristics of three typical sections(I、II、III)

表2 半圆堤整体稳定性分析数据表Tab.2 Results of sem i-circular breakwater′s integral stability analysis
由表2可知,三个半圆堤断面在竖向承载力上满足要求,且不会产生滑移破坏。但在波浪循环荷载作用下,土体产生弱化,导致极限承载力下降。断面I所承受的总水平波浪力小于断面可承受的极限水平荷载,所以稳定;断面II所能承受的极限水平力与实际波浪力很接近,说明处于临界状态;而断面III的总水平波浪力比极限承载力大,说明处于不稳定状态。结果与实际情况相符,说明采用归一出的简化计算公式来判别循环荷载作用下半圆堤整体稳定性是可靠的,具有较好的应用前景。
5 结 语
1)在有限元软件ABAQUS上建立基于循环强度与D-P屈服准则相结合的拟静力模型,以此来分析循环荷载作用下半圆堤的整体稳定性。将纯黏土基础上的有限元解与其他近似解进行了对比,结果显示有限元模型计算荷载破坏包络线是准确可靠的。
2)分析了半圆堤在水平荷载和竖向荷载共同作用下荷载破坏包络线的变化趋势,给出了提高半圆堤整体稳定性的工程设计建议。
3)对变量进行无量纲化,通过优化拟合归一出描述循环荷载作用下考虑土体强度弱化时半圆堤整体稳定性极限状态方程。并以工程实例对简化计算公式进行了验证,结果显示提供的计算方法是准确可靠的,可供工程设计借鉴和参考。
[1] 范期锦,李乃扬.长江口二期工程北导堤局部破坏的原因及对策[J].中国港湾建设,2004,4(2):1-8.
[2] JTJ250-98,港口工程地基规范[S].北京:人民交通出版社,1998.
[3] Andersen K H,Kleven A,Heien D.Cyclic soil data for design of gravity structures[J].Journalof Geotechnical Engineering,ASCE,1988,114(5):517-539.
[4] Wang J H,Li C,Moran K.Cyclic undrained behaviorof soft claysand cyclic bearing capacity of a single bucket foundation[C]∥Proceeding of 15th International Offshore and Polar Engineering Conference.2005,2:377-383.
[5] 张其一.复合加载模式下地基极限承载力与安定性的理论研究及其数值分析[D].大连:大连理工大学,2008.
[6] JTJ298-98,防波堤设计与施工规范[S].北京:人民交通出版社,1998.
[7] Bolton M D.A guide to soilmechanics[R].London:Macmillan,1979.
[8] Vesic A S.Bearing capacityof shallow foundations[C]∥Winterkorn H F,Fang H Y.Foundation Engineering Handbook.New York:Van Nostrand-Reinhold,1975:121~147.
[9] 黄明毅.波浪力作用下半圆体结构地基应力分析研究[J].水运工程,2006(12):34-41.
[10] 余聿修,张宁川,饶永红.半圆堤的水力特性研究[J].海洋工程,1999,17(4):39-48.
Research on calculation methods for integral stability analysisof semi-circular breakwater under cyclic loading
ZHOU Bao-yong,WANG Yuan-zhan,YU Jian-xing
(Key Lab of Port and Ocean Engineering,Ministry of Education and Tianjin,Schoolof Civil Engineering,Tianjin University,Tianjin 300072,China)
U656.2
A
1005-9865(2011)01-0116-06
2010-07-26
国家自然科学基金资助项目(50979069);国家高技术研究发展(863)计划资助项目(2008AA09Z307)
周宝勇(1986-),男,福建泉州人,博士生,主要从事港口海岸及近海工程结构设计理论和方法、大型工程结构物可靠性分析优化及风险评估等研究工作。E-mail:abaozhou1986@163.com

