基于四阶完全非线性Boussinesq水波方程二维波浪传播数值模型
房克照,邹志利
(大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)
基于四阶完全非线性Boussinesq水波方程二维波浪传播数值模型
房克照,邹志利
(大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)
建立基于四阶完全非线性Boussinesq水波方程的二维波浪传播数值模型。采用 Kennedy等提出的涡粘方法模拟波浪破碎。在矩形网格上对控制方程进行离散,采用高精度的数值格式对离散方程进行数值求解。对规则波在具有三维特征地形上的传播过程进行了数值模拟,通过数值模拟结果与实验结果的对比,对所建立的波浪传播模型进行了验证。同时,为了考察非线性对波浪传播的影响,给出和上述模型具有同阶色散性、变浅作用性能但仅具有二阶完全非线性特征的波浪模型的数值结果。通过对比两个模型的数值结果以及实验数据,讨论非线性在波浪传播过程中的作用。研究结果表明,所建立的Boussinesq水波方程在深水范围内不但具有较精确的色散性和变浅作用性能,而且具有四阶完全非线性特征,适合模拟波浪在近岸水域的非线性运动。
Boussinesq水波方程;波浪传播模型;波浪破碎;涡粘
Abstract:The present study develops a 2Dwave breakingmodel based on the fourth-order full nonlinear Boussinesq equations.This setof equations possesses higher accuracy in dispersion,shoaling and full nonlinearity characteristics,which enable it applicable in describingwater waves in nearshore zone.The discretizationis conducted on a rectangle grid system,higherorder finite difference formulasare used to approximate the spatial derivatives and high accuracy scheme is used to integrate equations in time.Kennedy et al′s eddy viscosity breakingmechanism is incorporated to mimicwave breaking.Themathematicalmodel is run to simulate waves transformation over typical three dimensional bathymetries.The numerical results are verified against available experimental data.The satisfactory agreement between numerical resultsand experimental data demonstrate the validation and efficiency of the presentwave breakingmodel.The effectof full nonlinearityonwave propagation is discussed by comparing the numerical resultswith those from Boussinesqmodelwith only the second-order full nonlinearity characteristics.
Key words:Boussinesqwave equations;wave propagationmodel;wave breaking;eddy viscosity
近几十年来,基于Boussinesq水波方程的波浪模型得到了长足的发展并被广泛用于模拟近岸区域各种波浪运动现象,见综述性文献[1]和[2]。建立这类波浪模型时,Boussiensq方程的性能是首要考虑的因素,方程的性能包括线性性能(色散性和变浅作用性能)和非线性性能(各阶非线性传递函数以及波幅离散性能)。Boussinesq水波方程的发展过程很大程度上是提高上述各种性能的过程,起初诸多研究着重于提高方程的线性性能,代表性的工作有Madsen和Sorensen[3]、Nwogu[4]等,而后来的研究表明非线性在Boussinesq模型中有非常重要的作用。目前,具有强非线性特征的波浪模型不断涌现,其中Madsen等[5]给出的方程以及Lynett和Liu[6]提出的多层模型颇具代表性。前者最大应用水深达到kh=40,但方程的数值求解过程涉及到大型稀疏矩阵的求解[7-8],即便对于一维问题控制方程多达6个,形成的稀疏矩阵带宽至少为25[9];后者通过适当增加模型层数,也可以得到性能较好的方程,但随着层数增加,控制方程增多,加大了数值求解工作的难度。相对而言,具有较低色散性精度但具有强非线性特征的方程数值求解简便,仍不失为进行波浪数值模拟的有力工具。Wei等[10]给出了具有二阶完全非线性特征的Boussinesq方程,基于此方程发展的二维模型FUNWAVE[11]得到了广泛的应用。Madsen和Schaffer[12]给出了具有四阶非线性特征的Boussinesq方程,其非线性达O(εμ4)阶(这里ε为表征方程非线性的参数,定义为ε=A/h,A和h分别为特征波幅、特征水深;μ=kh为色散性参数,k为特征波数);Gobbi和Kirby[13]给出了具有四阶完全非线性特征的Boussinesq方程FN4;Zou和Fang[14]也推导了具有四阶完全非线性的Boussinesq方程BouN4D4。上述模型的相关研究成果均表明,具有强非线性特征的方程较仅具有弱非线性特征的模型有优越性,更适合模拟波浪的非线性运动。因此,建立具有强非线性特征的波浪模型非常必要,然而上述模型中,FUNWAVE虽然具有二阶完全非线性特征,但方程色散性仅为精确色散关系的Pade[2,2]阶近似,限制了模型在深水范围的应用;Madsen和Schaffer[12]给出的方程仅具有弱非线性特征同时并未建立相应的数值模型;上述两个具有完全非线性特征的方程(FN4和BouN4D4)虽然具有强非线性特征,但所建立的模型仅限于一维问题,也并未考虑波浪的破碎问题,而具有四阶完全非线性特征的二维波浪模型更加鲜见。建立基于BouN4D4的二维波浪模型,该方程除具有四阶完全非线性特征外,其色散性为精确色散关系的Pade[4,4]阶近似,适用于深水波浪问题,同时具有良好的变浅作用性能。在矩形网格上对控制方程进行离散,建立高精度数值格式,考虑波浪的破碎问题。针对几个典型三维地形上波浪进行数值模拟,通过对比分析数值结果和实验数据,考察非线性特征在波浪传播过程中的作用,同时验证具有四阶完全非线性特征波浪传播模型的有效性。
1 数值模型
1.1 Boussinesq方程
Zou和Fang[14]推导了具有四阶完全非线性特征的Boussinesq水波方程,该组方程以波面η和水深平均速度¯u表达,经扩展后(考虑波浪破碎、水低摩擦等效应)方程的二维无因次形式为
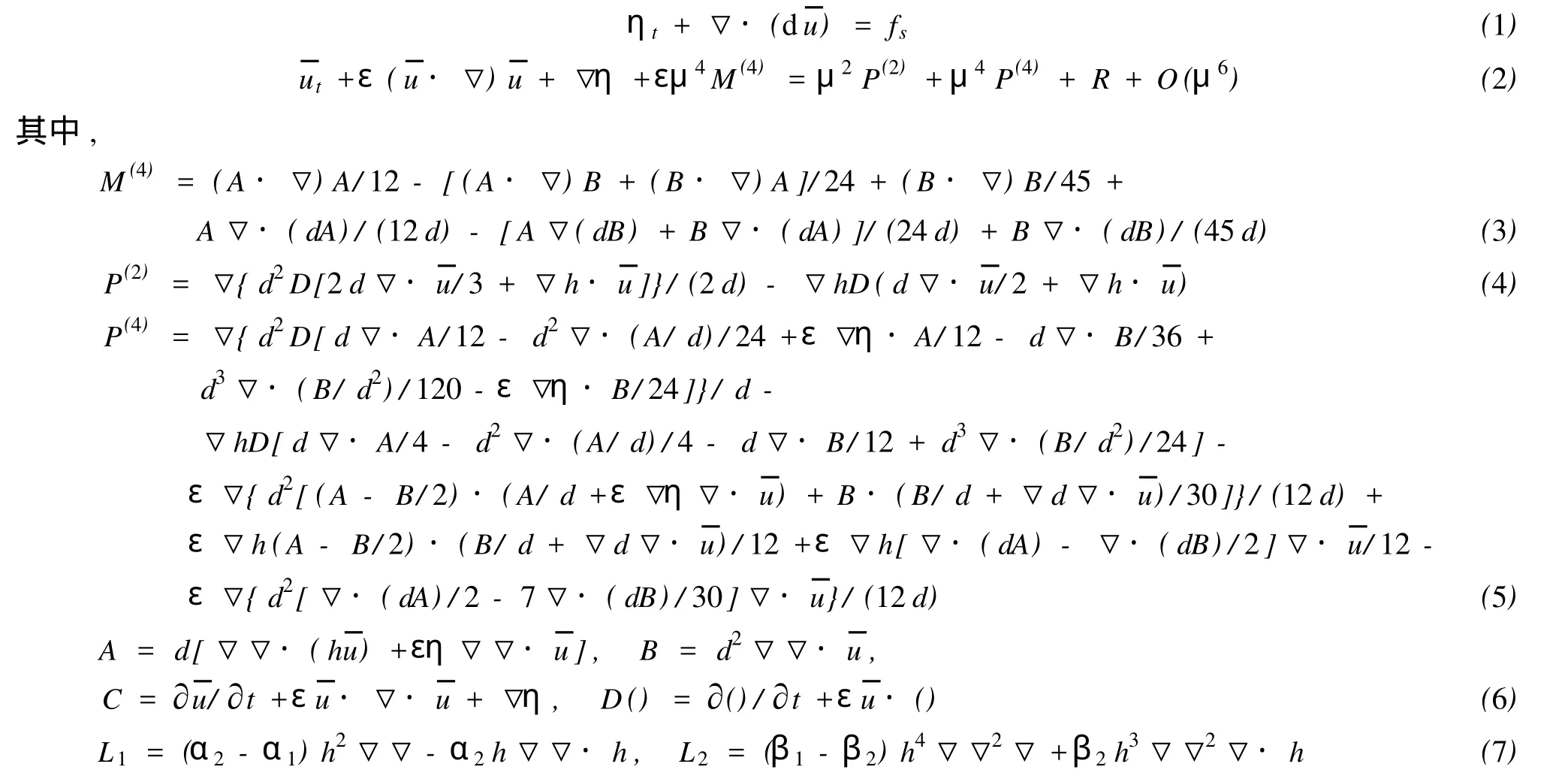
式中:¯u为水深平均速度,η为波面升高,h为静水深,d=h+εη为当地水深,g为重力加速度,▽=(∂x,∂y)为二维偏微分算子 ,α1=1/9,β1=1/945,α2=0.146 488,β2=0.001 996 为常数 ,其中α1、β1确定了方程的色散性,α2、β2决定了方程的变浅作用性能。上式中R定义为R=Rf+Rb+Rs+Rm,其中Rf代表底摩擦阻力,Rb、Rs、Rm分别为波浪破碎引起的耗散项、海绵吸收层和侧混项,其表达式同FUNWAVE中一致,fs为内域波浪生成时引入的源函数,同Gobbi和 Kirby[13]给出的一致。
后文中将上述模型称为BouN4D4,N4代表4阶完全非线性,D4代表色散关系为精确色散关系的Pade[4,4]阶近似。该方程保留了精确到O(μ4)阶的所有非线性项,最高阶达O(ε5μ4),使得方程具有四阶完全非线性特征,更适合描述具有非线性特征的波浪运动现象,方程的推导以及性能分析过程见文献[14]。忽略上述方程中所有O(μ4)阶非线性,则得到仅具有二阶完全非线性特征的方程,称之为BouN2D4(N2代表2阶完全非线性,D4代表色散关系为精确色散关系的Pade[4,4]阶近似),其将用于和BouN4D4进行对比,以考察非线性在波浪传播过程中的作用。
1.2 数值求解
有限差分方法由于具有直观性和容易程序实现的优点,被广泛用来数值求解Boussinesq方程,发展得比较完善,如FUNWAVE[11]以及 Gobbi和 Kirby[13]。因此,这里仍然采用有限差分方法对上述方程进行数值求解,但值得注意的是若采用传统的手工编程方法对方程(1)~(7))进行程序实现非常繁琐,而通过充分利用MAPLE强大的数学公式推导功能及其向Fortran语言的转化功能,可实现快速、准确地撰写程序代码的目的。文中采用的数值求解格式同上述文献基本类似,这里不再一一详述,详细过程可参考上述相关文献,下面仅给出主要步骤。
1.2.1 方程整理
将方程中含时间导数的线性项移在方程左侧,其它项移至方程右侧:

注意,上式中ξ,U,V中包含了所有含ηt,,的线性项。E,Et,F,Ft以及G,Gt分别为质量方程,动量方程中剩余的所有空间项和时间项,r项为式(2)中R在x,y方向的分量。
1.2.2 方程离散及差分公式
在图1所示的矩形网格上对控制方程进行空间离散,x,y方向网格标记分别为i(i=1,mi)和j(j=1,mj)。对于方程右端空间导数采用七点差分格式,内点采用中心格式,边界点采用偏心格式,对于单方向的差分统一用如下公式表示

式中:δfl表示函数在f网格点l处的空间导数(i-3≤l≤i+3)。当l=i时为中心差分,当l≠i时为偏心差分,γ,αm为差分格式的系数,其具体取值以及各阶差分格式精度参见附录A.1。对于水平二维问题,还涉及到交叉导数项,其具体实施办法在附录A.2中列出。可以看出,对于任意一个内点(i,j),其差分近似涉及到周围25个点,见图1。对于方程左端线性时间项的系数采用五点中心差分格式,则按上述网格离散后,形成一个系数矩阵带宽为五的线性方程组。对于方程右端对时间的一阶导数项,采用 Gobbi和 Kirby[13]文中公式进行计算,这里不再给出。

图1 空间离散示意以及差分模板Fig.1 The sketch of spatial discretization and difference stencil
1.2.3 时间积分、边界处理等
按照上述网格以及差分公式对方程离散后,采用五阶Adams-Bashforth预报,六阶Adams-Moulton校正格式进行时间步进求解。对于波浪入射边界、固壁边界的处理同用 Gobbi和 Kirby[13]文中完全一致(注意文献中为一维),不再给出。波浪传播过程中,由于非线性或者地形突变容易引起高频数值震荡,计算中采用SG光滑技术[7]对数值结果进行光滑处理。
2 模型验证和对比
将对上面建立的数值模型进行验证,针对几个典型三维地形进行波浪传播的数值模拟。通过对比数值模拟结果和实验结果对模型进行验证;对比模型BouN4D4和BouN2D4的数值结果,讨论非线性作用在波浪传播过程中的作用。
2.1 圆型浅滩上波浪的传播
Chawla和Kirby[15]进行了波浪跨通过圆型浅滩传播的实验(见图2)。该实验在水池中进行(长18 m,宽18.2m),水池中央放置圆型浅滩,其半径为2.57m,浅滩中心位于(x=8.0 m,y=8.98 m)处,在七个不同断面上进行波高测量。图2为计算区域以及测量断面示意图,取计算域长23m,宽18.2 m,在计算域两端分别设置2m、3m的海绵层,两侧面为固体边界,空间网格步长为0.10 m,时间步长0.02 s,每0.1个周期对波面和速度应用一次SG光滑器。这里仅选取其中两组规则波实验进行模拟。其中,第一组波浪没有发生破碎,其对应的波浪要素为水深0.45 m(圆型浅滩顶部水深0.08m),波高0.011 8m,周期1 s;第二组存在波浪破碎现象,对应的波浪要素为水深0.395m,波高0.02m,周期1 s。该实验中除浅滩外均为常水深,这将导致波浪在浅滩后产生较强的波浪幅聚现象。
对波浪不破碎情况,模型运行40 s,取最后6 s的数据进行波幅计算(30 s以后波浪场基本达到稳定状态)并将结果在图3中给出。可以看出,BouN4D4和BouN2D4的数值结果基本重合,同时和实验数据吻合良好,这表明这一算例对高阶非线性的要求较低。沿断面A-A,模型较准确地模拟了由于波浪浅化引起的波高增大现象以及浅滩后波高减小现象。还可以看出,浅滩处波高几乎高达入射波高的2.7倍,这进一步表明该处有强烈的波浪汇聚现象。对于其它的测量断面,模型也给出了较好的模拟结果,这表明其较准确地模拟了波浪的折射、绕射过程。从图中还可以看出,由于浅滩的位置并未处于计算域中心位置,计算结果和实验数据关于浅滩中心轴线并不完全对称。
对于波浪破碎情况,模型运行50 s,取最后10 s数据进行均方根波高计算,图4给出了数值结果同实验数据的对比(图中H0为入射波高)。可以看出,BouN4D4和BouN2D4给出的数值结果相近,但较波浪不破碎情况差异加大,这可能是由于入射波浪非线性增强所致。在断面E-E之前,BouN4D4在y=10m区域附近给出的幅值略高于BouN2D4并且更接近实验数据;在浅滩顶部(断面F-F),两模型模拟的波高均高于实验值但BouN4D4较BouN2D4和实验数据吻合程度稍好。总体而言,两个模型的数值表现良好,但较不破碎情况差。这可能是由于以下几个原因:1)用于模拟波浪破碎的涡粘公式是经验性的,不能很好地描述波浪破碎这一复杂物理现象,同时由于实验中波浪破碎时具有三维特征,而采用的涡粘方法在数值实现时仅能沿某几个固定方向对波浪破碎进行捕捉,存在误差;2)波浪破碎时波面会变得非常陡峭,因此为了更好地刻画波面,计算时所用的空间、时间步长要比较小,但出于计算时间和对比考虑,这里参数的取值同第一个算例一致。
图5给出了针对这两个算例t=35 s时的波面瞬时图。可以看出,由于波浪的浅化、折射、绕射以及非线性的相互作用,最终的流场呈现复杂的三维形态。其中,波浪不破碎和破碎两种情况存在以下共同特征:波峰在浅滩上发生了弯曲,这是由于波浪折射所致,同时由于波浪浅化作用波高增大;在浅滩末端出现了明显的波浪汇聚现象;由于浅滩的存在其后部都存在波浪掩护区;观察波峰线,都明显存在波浪绕射现象。不同的是:波浪破碎情况下,浅滩上波面极其陡峭并且最大值出现在浅滩上,而波浪不破碎时浅滩上波面变化较缓且最大值出现在浅滩末端。
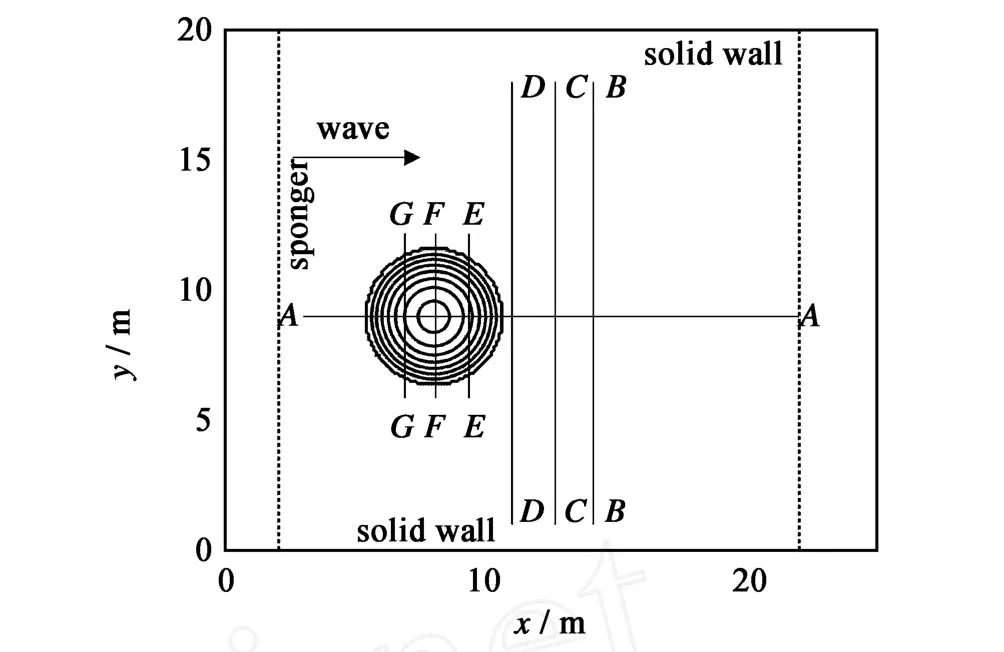
图2 Chawla和kirby实验布置以及测量断面分布Fig.2 Experiment setup and measurement transects(Chawla and Kirby)
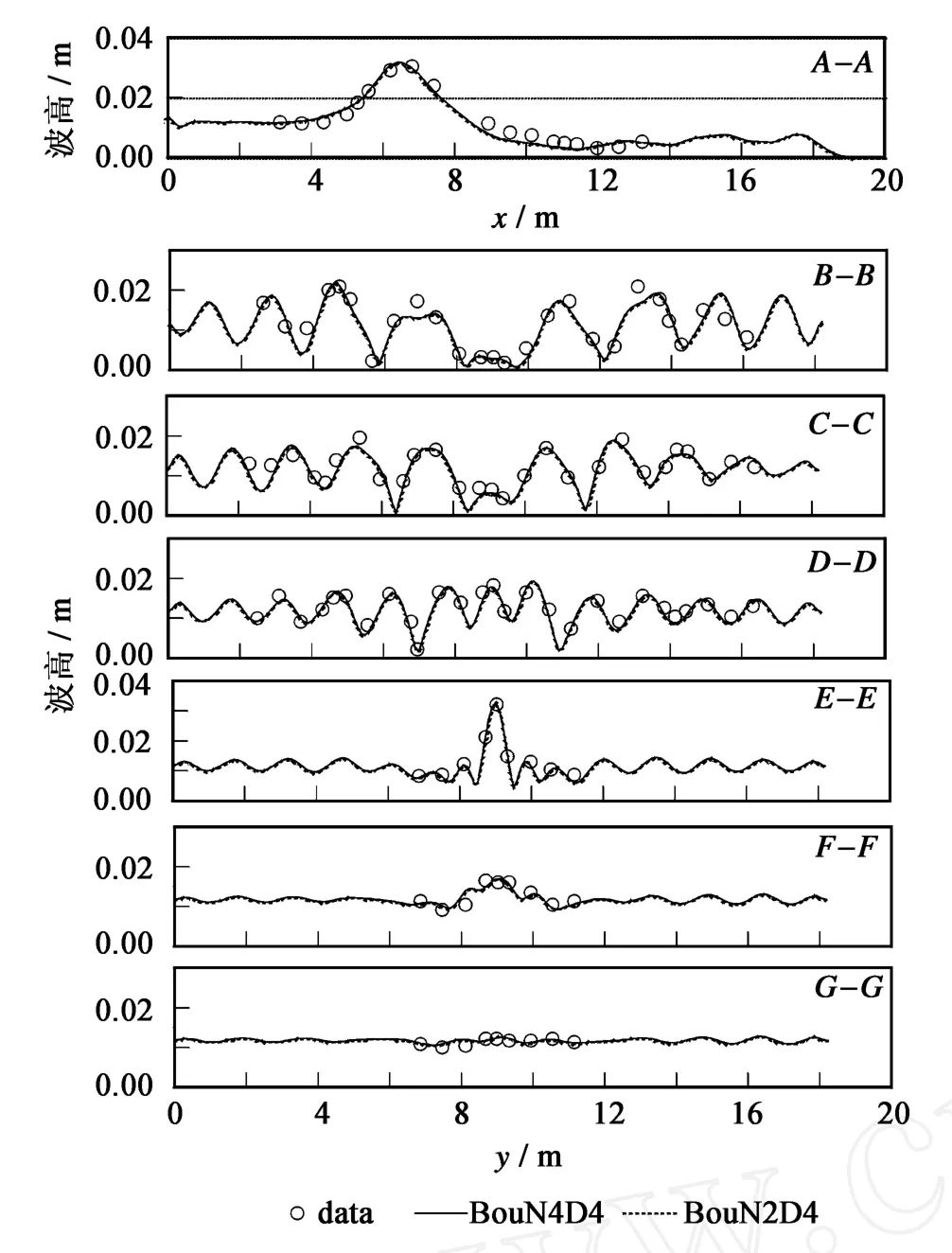
图3 各测量断面波高分布Fig.3 Wave height comparisons along different transects
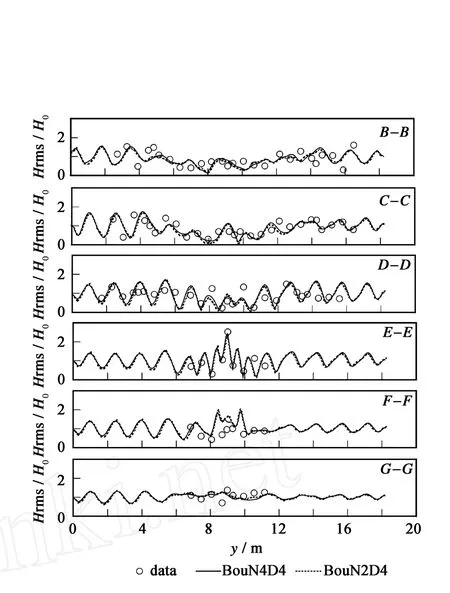
图4 各测量断面波高分布Fig.4 Wave height comparisons along different transects

图5 稳态后流场波高分布示意(BouN4D4)Fig.5 Elevation contoursof the steadywave fields(BouN4D4)
图6给出了流场的时均流速图。可以看到,在潜堤顶端,由于波浪破碎引起强烈的水流,幅值明显大于其它区域波浪运动的水流速度。这同一般的波浪破碎理论相吻合,波浪破碎总是伴随着流的产生,实验过程中也观测到了这一现象[15]。
2.2 凸型浅滩上波浪的传播

Whalin[16]在波浪水槽中进行了一系列波浪在浅滩上的非线性折射和绕射物理实验,实验水槽尺度为25.603m×6.096m。实验地形由以下公式给出式中:所有变量单位为米。图7为计算域以及地形示意图。在图示地形上,波浪会发生变浅幅聚作用,由于非线性作用高次谐波变得尤为突出。因此,该实验被广泛地用来验证各类波浪模型[7-8,18]。实验可按照波浪周期不同分为三组,各组波浪要素及计算参数取值见表1,从表中可以看出,对应于某一周期,入射波浪的非线性依次增强,因此通过对这些工况的模拟,可以考察模型非线性精度对数值模拟结果的影响。下面,将模型BouN4D4和BouN2D4分别用于模拟Whalin的实验并进行对比分析。
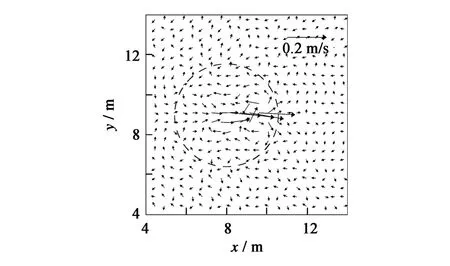
图6 流场时均流速分布Fig.6 Phase-averaged velocity field
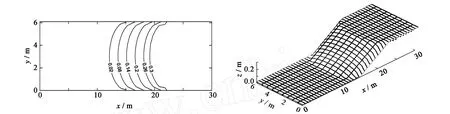
图7 计算域及地形示意Fig.7 The computation domain and bathymetry sketch
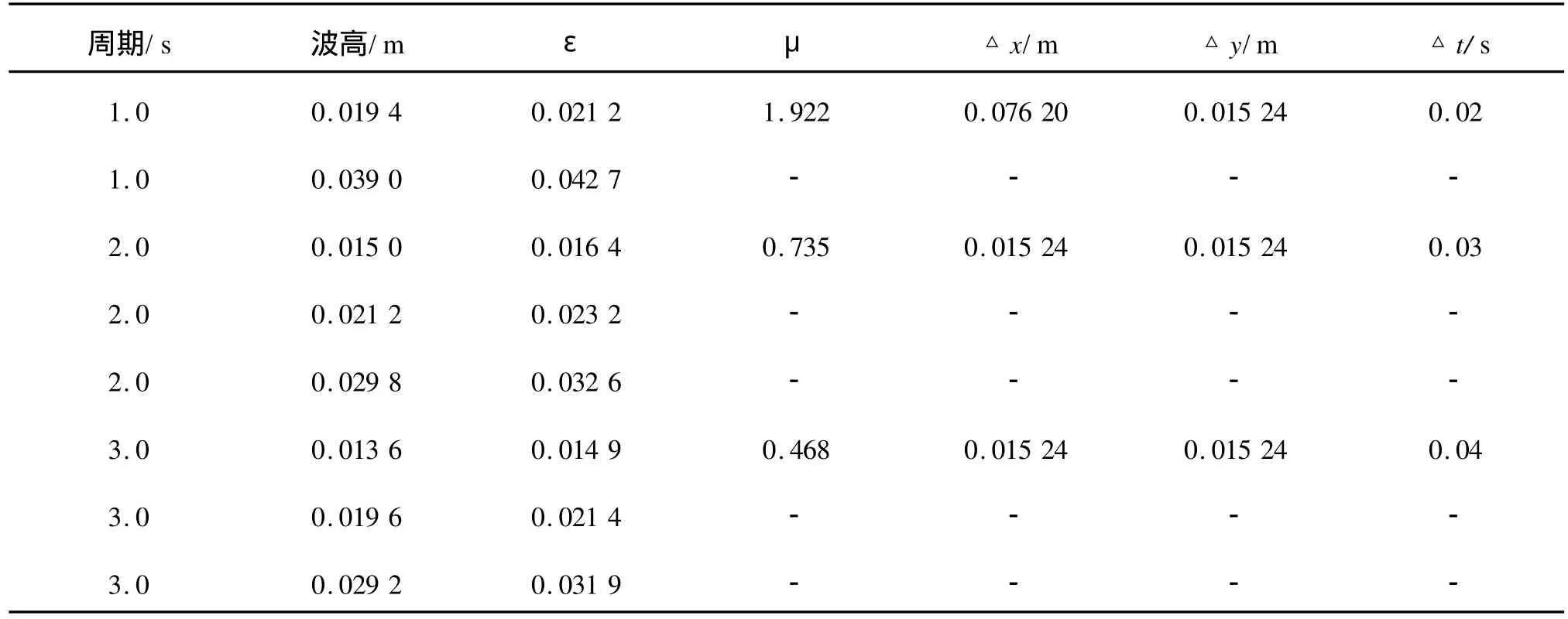
表1 Whalin实验波浪要素及数值模拟网格尺寸Tab.1 Wave conditions for Whalin experiment and grid size in simulations
图8给出了T=1 s时,模型BouN4D4和BouN2D4的计算结果同实验数据的对比。可以看出,数值结果同实验数据吻合良好。其中,当H=0.019 4 m时,两个模型的数值结果几乎没有差别,都较好地模拟了各次谐波沿空间的变化,但随着波浪非线性的增强,两个模型的差异变大,即当H=0.039 m时,BouN2D4给出的数值结果在x大于15 m时高于BouN4D4的数值结果,而BouN4D4和实验数据更为接近。由于两模型的色散性相同因此这一差别反映了非线性对数值结果的影响。图9给出了T=2 s时,模型BouN4D4和BouN2D4的计算结果同实验数据的对比。可以看出,随着波浪非线性增强模型表现出的差异增大,这与上一算例一致,不同的是,两个模型的数值结果差别较大。具体的,BouN2D4模拟的一、二次谐波幅值均高于实验数据和BouN4D4的结果而后者同实验数据更为吻合,其中一次谐波差别最大。对于三次谐波,BouN2D4给出的结果同实验数据吻合良好而BouN4D4模拟的幅值略低于实验数据,但考虑到三次谐波的幅值非常小(毫米量级),这一不足可以忽略。由于两个模型的色散性以及变浅性能相同,因此这一差别反映了非线性对数值结果的影响。图9也给出了T=3 s时,模型BouN4D4和BouN2D4的计算结果同实验数据的对比。可以看出,模型结果同实验数据差别较大,目前所见各类模型普遍存在这一现象[7-8,18]。不同于上述两个算例,两模型的数值结果几乎没有差别,这是由于该算例值最小,两模型的非线性性能曲线在此处差别较小所致。因此,对于Whalin的实验,当周期较小,非线性较大时,模型的非线性性能对数值结果的影响较大,总体而言,BouN4D4模拟的数值结果较BouN2D4更接近实验数据。
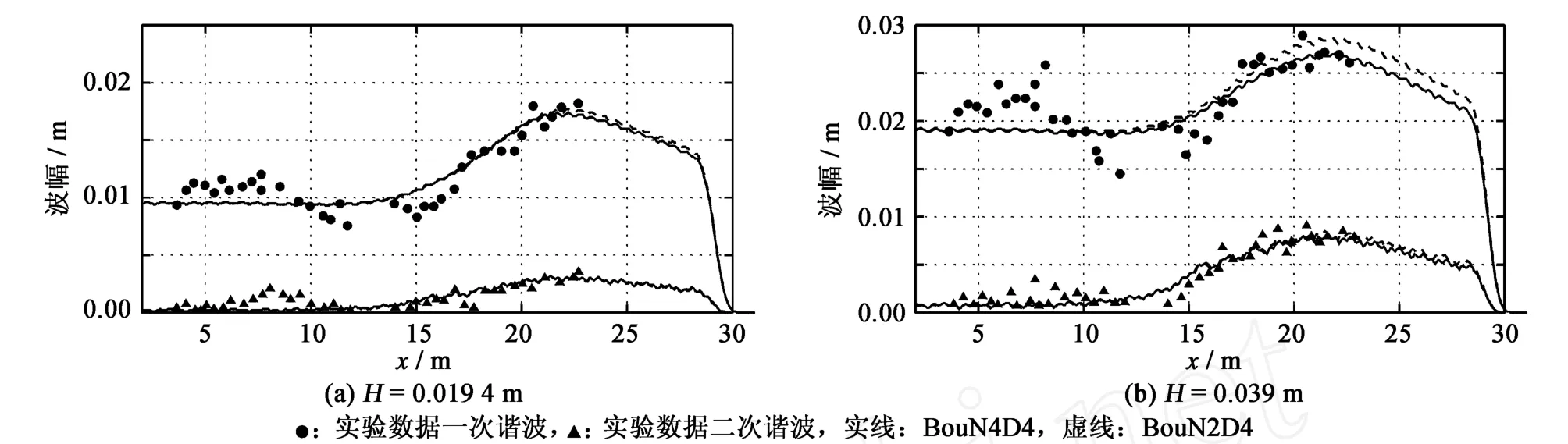
图8T=1.0 s时谐波幅值对比Fig.8 Comparisonsof harmonic amplitude forwave periodT=1.0 s

图9 不同时刻谐波幅值对比Fig.9 Comparisonsof harmonic amplitude forwave periodT=2.0 s(left)andT=3.0 s(right)
3 结 语
建立基于四阶完全非线性Boussinesq水波方程的二维波浪破碎模型。选用的控制方程BouN4D4具有强非线性特征同时具有较好的色散性和变浅作用性能,更适合于描述波浪的非线性运动。在矩形网格上对上述方程进行空间离散,采用高阶导数近似方程中的时、空间导数,用高精度ABM预报校正格式进行时间积分,建立了高精度的数值求解格式,同时通过采用Kennedy等的涡粘破碎方法处理波浪破碎问题。
将所建立的具有四阶完全非线性特征的波浪传播模型BouN4D4和仅具有二阶完全非线性特征的模型BouN2D4用于模拟规则波在具有三维特征地形上的传播过程。通过对比两个模型的数值结果以及相关的实验数据,验证了所建立模型的有效性,讨论分析了非线性在波浪传播过程中的作用。结果表明:1)实验数据同数值结果吻合良好,这表明本研究所建立的模型可以较准确的模拟波浪在三维地形上的传播、破碎过程;2)入射波浪非线性较强时,模型的强非线性特征发挥较大作用,具有抑制波幅过度增长的作用。
[1] Kirby J T.Boussinesqmodels and application to nearshorewave propagation,surfzone processes and wave-induced currents[M]∥advances in Coastal Engineering.Lakhan V C(ed),Elsevier,2003:1-41.
[2] 李孟国,王正林,蒋德才.近岸波浪传播变形数学模型的研究与进展[J].海洋工程,2002,20(4):43-57.
[3] Madsen PA,Sφrensen O R.A new form of the Boussinesq equationswith improved linear dispersion characteristics.Part 2:A slowlyvarying bathymetry[J].Coast.Engrg.,1992,18:183-204.
[4] Nwogu O.An alternative form of the Boussinesq equations for nearshorewave propagation[J].J.Wtrwy,Port,Coast.and Oc.Engrg.,1993,119:618-638.
[5] Madsen PA,Bingham H B,Schaffer H A.Boussinesq-type formulations for fully nonlinear and extremely dispersive water waves:derivation and analysis[J].Proc.R.Soc.London.A,2003,459(2033):1075-1104.
[6] Lynett P,Liu PL F.A two layer approach to wavemodelling[J].Proc.R.Soc.London.A,2004,460:2637-2669.
[7] Fuhramn D.Numerical solutionsof Boussinesq equations for fully nonlinear and extremely dispersivewaterwaves[D].Denmark:Technical Univ.of Denmark,2006.
[8] 王本龙.基于高阶Boussinesq方程的海岸破波带数学模型研究[D].上海:上海交通大学,2005.
[9] 张洪生,冯文静,王亚玲,等.非线性波传播的新型数值模拟模型及其实验验证[J].海洋学报,2007,29(4):137-147.
[10] Wei G,Kirby J T,Grilli ST.A fully nonlinear Boussinesqmodel for surfacewaves.Part I.Highly nonlinear unsteadywaves[J].J.Fluid Mech.,1995,294:71-92.
[11] Kirby J T,Wei G,Chen Q,et al.FUNWAVE 1.0,Fully nonlinear Boussinesq wavemodel documentation and user′smanual[R].CACR search report,University of Delaware,1998:CACR-98-06.
[12] Madsen PA,Schäffer H A.Higher-order Boussinesq-type formulation for surface gravity waves:Derivation and analysis[J].Phil.Trans.R.Soc.Lond.A,1998,356:3123-3184.
[13] Gobbi F,Kirby J T.Wave evolution over submerged sills:testsof a high-order Boussinesqmodel[J].Coast.Engrg.,1999,37(1):57-96.
[14] Zou Z L,Fang K Z.Alternative forms of the higher-order Boussinesq equations:Derivations and validations[J].Coast.Engrg.,2008,55(6):506-521.
[15] Chawla A,Kirby J T.Wave transformationover a submerged shoal[R].CACR research report,University of Delaware,1996:CACR-96-03.
[16] Whalin RW.the limitof applicability of linearwave refraction theory on a convergence zone[R].Res.Rep.,Vicksburg,MS:U.S.Army Corpsof Engineers,Waterways Expt.Station.1971:Res.Rep.H-71.
[17] Kennedy A B,Chen Q,Kirby J T,et al.Boussinesqmodeling of wave transformation,breaking,and runup[J].I:1D.J.Wtrwy,Port,Coast.and Oc.Engrg.,2000,47:39-47.
[18] Chan Y,Liu PL F.Modified Boussinesq equations and associated parabolicmodels forwaterwave propagation[J].J.Fluid Mech.,1995,288:351-381.
附录:
1 单方向差分格式
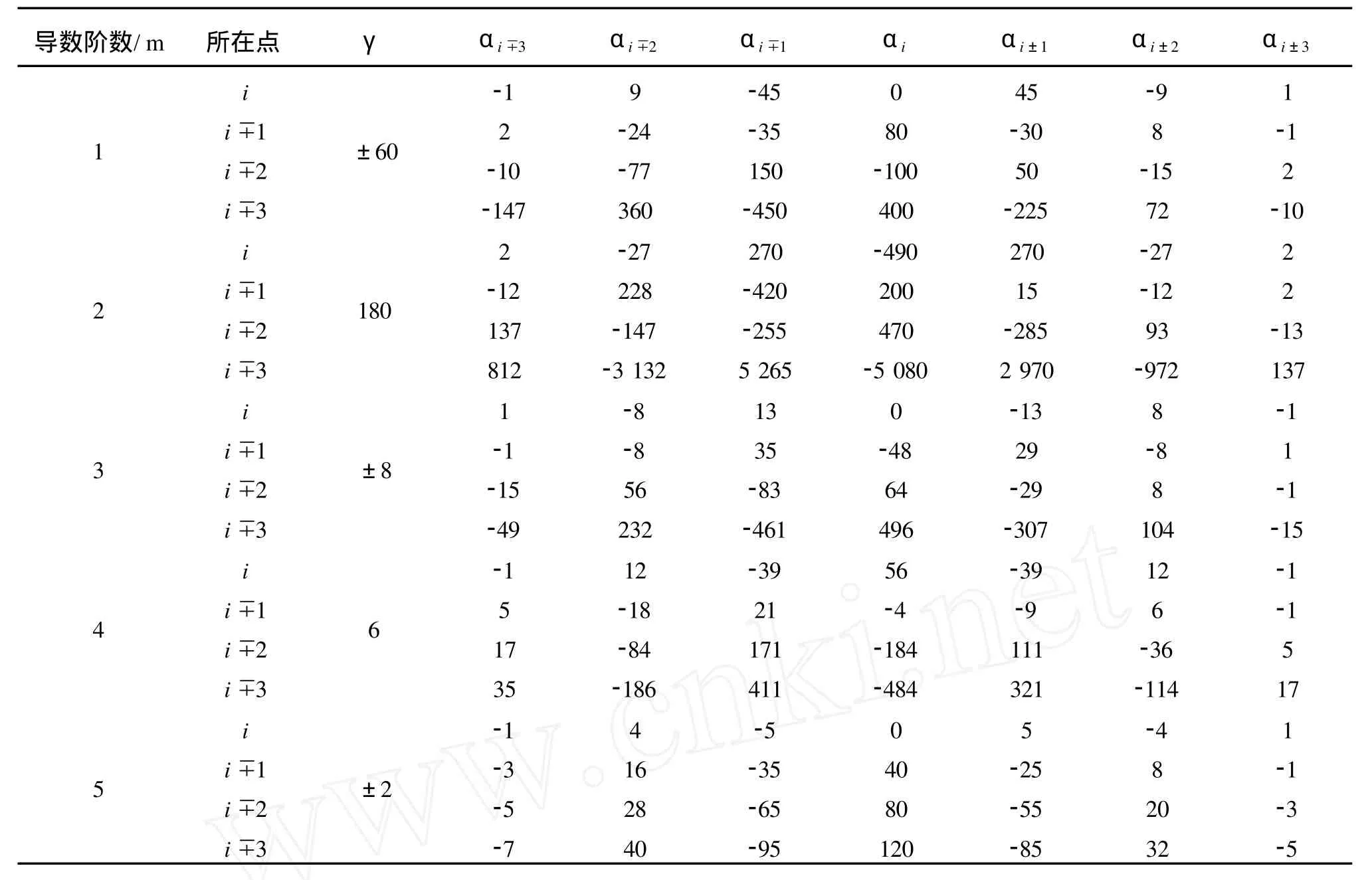
导数阶数/m 所在点 γ αi∓3 αi∓2 αi∓1 αi αi±1 αi±2 αi±3i90 1i∓1i∓2i∓3±60-12-98-10-147-24-77 360-45-35 150-450 80-100 400 45-30 50-225-15 72 1-12-10 2 3 4ii∓1i∓2i∓3i i∓1i∓2i∓3i i∓1i∓2i∓3 180±8 6 2-12 137 812 1-1-15-49-151 7 35-27 228-147-3 132-8-85 6 232 12-18-84-186 270-420-255 5 265 13 35-83-461-39 21 171 411-490 200 470-5 080 0-48 64 496 56-4-184-484 270 15-285 2 970-13 29-29-307-39-9 111 321-27-12 93-972 8-88 104 12 6-36-114 22-13 137-11-1-15-1-151 7i4-505 5i∓1i∓2i∓3±2-1-3-5-7 16 28 40-35-65-95 40 80 120-25-55-85-482 0 32 1-1-3-5
2 混合导数差分格式
混合导数差分格式可以表示为

式中:m和n分别表示沿x,y方向导数的阶数;Fm,n为系数矩阵,分别为

对于F1,2,F2,3,F1,3,F1,4则可通过对上面公式的简单变换得到。
A 2D numericalwavemodel based on fourth order fully nonlinear Boussinesq equations
FANG Ke-zhao,ZOU Zhi-li
(The State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)
TV148
A
1005-9865(2011)01-0032-09
2010-04-07
中央高校基本科研业务费专项资金资助项目;大连理工大学海岸和近海工程国家重点实验室、河海大学海岸灾害及防护教育部重点实验室开放基金资助项目;国家自然科学基金资助项目(51009018)
房克照(1980-),男,山东日照人,讲师,博士,从事海岸工程研究。E-mail:kfang@dlut.edu.cn

