局部微分求积法的深水包络孤立波数值模拟
张 弩,宗 智,于 馨
(大连理工大学工业装备结构分析国家重点实验室船舶工程学院,辽宁 大连 116024)
局部微分求积法的深水包络孤立波数值模拟
张 弩,宗 智,于 馨
(大连理工大学工业装备结构分析国家重点实验室船舶工程学院,辽宁 大连 116024)
利用局部微分求积法(LDQ)对非线性薛定谔(Schrödinger)方程进行数值求解,分别模拟了单深水孤立波运动,同向双深水孤立波追赶碰撞耦合运动,高阶孤立波振动和孤立波的反射与透射现象,得到各情况下的数值结果。从数值模拟及图像中揭示非线性薛定谔方程的性质和特点,阐述深水孤立波形成的物理意义、运动方式和运动规律,分析在不同初值条件下波形的变化特点,验证了LDQ法对该类问题的有效性。
局部微分求积法;孤立波;非线性薛定谔方程;数值模拟
Abstract:The nonlinear Schrödinger equation describes the evolution of the envelope ofmodulated wave groups.This equation has soliton solutions.Numerical simulationsof Nonlinear Schrödinger Equation are studied using localized differential quadraturemethod.Propagation of a deep-water soliton and interactionof two deep-water solitons in the same direction,the Higher-order soliton′s vibration and the soliton′s reflection and transmission are simulated.The numerical results of every case are obtained.The properties and characteristics of the nonlinear Schrödinger equation areobtained from numerical simulationsand images.The physicalmeanings,motionmodesandmotion lawsof deep-water solitons are discussed.Thewaveform changes at different initial conditions are analyzed.The validity of LDQ method for solving this kind of problems is proved.
Key words:localized differential quadraturemethod;soliton;nonlinear Schrödinger equation;numerical simulation
非线性薛定谔(Schrödinger)方程描述了深水调幅波群的包络随时间的演化。该方程存在孤立波解。对非线性薛定谔波浪传播方程的求解对于研究深水包络孤立波具有重要的理论和实际意义。
关于某些特殊情况的非线性薛定谔方程的解析解,以及精确孤立波解,学者们提出了许多精巧的方法,如行波解法[1];Jacobi椭圆函数展开法[2];分数变换法[3];反散射方法[4];分步傅里叶法[5];齐次平衡法[6];李群约化法[7]等等。但非线性薛定谔方程作为一个非线性偏微分方程,在更一般的情况下无法求出解析解,因此需要进行数值分析探寻其数值解。
孤立波是一种特殊的水波,具有保持其波形和速度不变的特点,孤立波之间能发生强烈的相互作用,但相互作用后仍能保持其各自特点、形状、速度不变。因此孤立波被称为自然界的相干结构,反映了非线性系统中的惊人有序性,孤立波理论的产生与发展是非线性偏微分方程研究中的一个重要组成部分。正是由于孤立波是这样一种非线性和色散的微妙平衡,在传播过程中始终保持稳定的速度和形状,所以对数值精度的要求很高,低精度的方法由于数值耗散,不能给出很好的结果。采用高精度的局部微分求积法(LDQ法)对其进行求解。
微分求积法(DQ法)的基本原理是Belman和Casti于1971年提出的[8],自提出以来DQ方法己被成功运用到许多工程物理中,其基本思想是函数对某一变量的偏导数可以由在此变量方向上所有离散点处的函数值的加权线性求和来逼近。这个方法数学原理简单,计算精度高,计算量少,使用方便,不依赖泛函和变分原理,边界条件不用另外考虑。但DQ法对不规则区域较难处理,对网格分布要求高,当节点增加到一定的数目时,系数矩阵会出现病态情况。为此学者们做了很多研究改进,简单并且有效的改进方法是局部微分求积法(LDQ法)[9]。LDQ法的基本原理是将某点的导数近似为此点附近局部节点的函数值及其加权系数的线性组合。LDQ法在具有DQ法优点的同时,出现了带状稀疏矩阵,为不规则区域的处理提供了可能。利用LDQ法将非线性薛定谔方程进行空间离散后,再利用经典4阶Runge-Kutta法在时域上离散,求得其数值解。
1 深水调幅波群的非线性薛定谔控制方程
深水调幅波群的非线性薛定谔方程表述[10]:

2 数值方法
LDQ方法基本思想是取与节点x(i)相近的m个节点(包括x(i))的函数值与其加权系数之和作为该节点的导数值。而其中的权系数不依赖于任何具体问题,只与网格剖分有关。该方法采用局部节点处理的方法,使其能够适用于某些复杂区域问题,当节点增加到一定的数目时,系数矩阵也不会出现病态情况。
由于LDQ方法中节点的近似函数值只与附近节点的函数值有关,因而采用在DQ法中的Chebyshev节点等非均匀节点则无必要,一般采用均匀分布节点即可满足精度要求。
LDQ方法的第一步是要找到所求节点的邻域。我们用:


由式(14)、(15)加上适当的初始条件,利用经典4阶Runge-Kutta法在时域上离散求得函数的数值解。
3 算例介绍
按以上数值方法编写Fortran程序,求解下列不同情况下的算例。
3.1 单孤立波的运动及验证
一种简单的孤立波解可以表述[10]:

将式(18)作为初始条件,代入Fortran程序中应用LDQ法进行求解。对于LDQ法,节点数越多,数值结果越精确[11]。取总节点数N=400,局部节点数m=5,已足够达到精确性要求。分别取t=0.0、1.0、2.0三个时刻的实部函数、虚部函数和包络线函数的数值解与包络线函数的解析解,函数图像如图1所示。

图1 不同时刻时单孤立波的运动Fig.1 Themotion of a soliton at different times
从图1中可以观察到,孤立波在行进途中始终保持稳定的速度和形状,不会分流成更小的波,也不会损失能量。孤立波能稳定传播的原因,在于孤立波在传播过程中同时存在色散效应和非线性的汇聚效应,且这两种效应的传播速度相反,当两种作用达到某种平衡时,才能出现波形和速度稳定的孤立波。
比较图1中包络线函数的数值计算解与解析精确解,二者吻合得很好,可见数值解充分逼近精确解,从而验证了数值计算的精确性。
3.2 两同向孤立波追赶碰撞耦合运动
两同向孤立波追击耦合运动,取初始条件:

分别取两孤立波的位置为-10.0与10.0处,按式(16),取ve1=8.0,ve2=2.0,φ0=1.0,q=2.0,则t=0时的初始条件:

将式(20)作为初始条件进行求解,取总节点数N=400,局部节点数m=5,得到各个时刻的函数图像。取函数的实部f(x,t)演示,如图2所示。

图2 不同时刻时两同向孤立波的耦合运动Fig.2 The interction of two deep-water solitons in the same direction at different times
根据图2可以看出,波速较快孤立波的载体波数较多,两孤立波追击相遇后,耦合成一道大约2倍振幅的大波,但交汇过后,两波又重新出现,逐渐分开,回复为碰撞前的形状。孤立子在碰撞的时候不满足一般线性波动的叠加原理,碰撞过程就像波速较快的孤波把波速较慢的孤波吞掉后,然后又把波速较慢的孤波吐了出来,并且各自都毫发无伤。这种现象很显然的是一种非线性的叠加,这也正是孤立波最重要的性质之一。本例中所模拟的深水孤立波与KdV方程所描述的浅水孤立波不同,KdV方程所描述的两浅水孤立波耦合后的合成波幅小于其中波幅较大者的幅度[12],而深水孤立波耦合后波幅会叠加增大。
3.3 高阶孤立波
求解高阶孤立波解的初始条件[13]:

系数M可为任意值,当M为整数时,为稳定孤立波,M=1时,为基本孤立波。取M=3的情况进行模拟,取总节点数N=400,局部节点数m=5,得到高阶孤立波振动的图像,取包络函数进行演示,如图3所示。
在输入的初始条件为对称性条件下,其输出的孤立波以相同速度传播。此时在群速度参考系中,所有孤立波的速度为零。当大量的孤立波以相同速度传播时,其叠加振幅由于孤立波间的相位干涉而出现振动特性。振动将产生非常大的波幅。
高阶孤立波在传播中波形发生周期变化,对于M=3的三阶孤立波在传播中变化很复杂。如图3,它在1/4周期(t=0.2)与3/4周期(t=0.6)处,形成了两侧各有一个小峰的高大尖峰,而在半周期处(t=0.4)那个高大的尖峰又分裂为两个峰。

图3 高阶孤立波的振动(M=3)Fig.3 The higher-order soliton′s vibration(M=3)
3.4 孤立波的反射和透射
孤立波在遇到不同介质等引起的不均匀时,在界面处会将一部分反射,而另一部分将透射过去。
按式(16)取孤立波的初值,取ve=4.0,φ0=1.0,总节点数N=400,局部节点数m=5,设界面在x=10处,即令x≤10时,式(14)~ (16)中的q=2.0,x>10时,q=1.0。则得到孤立波入射到一个界面时的反射和透射的数值模拟,取函数的实部f(x,t)进行演示,如图4所示。
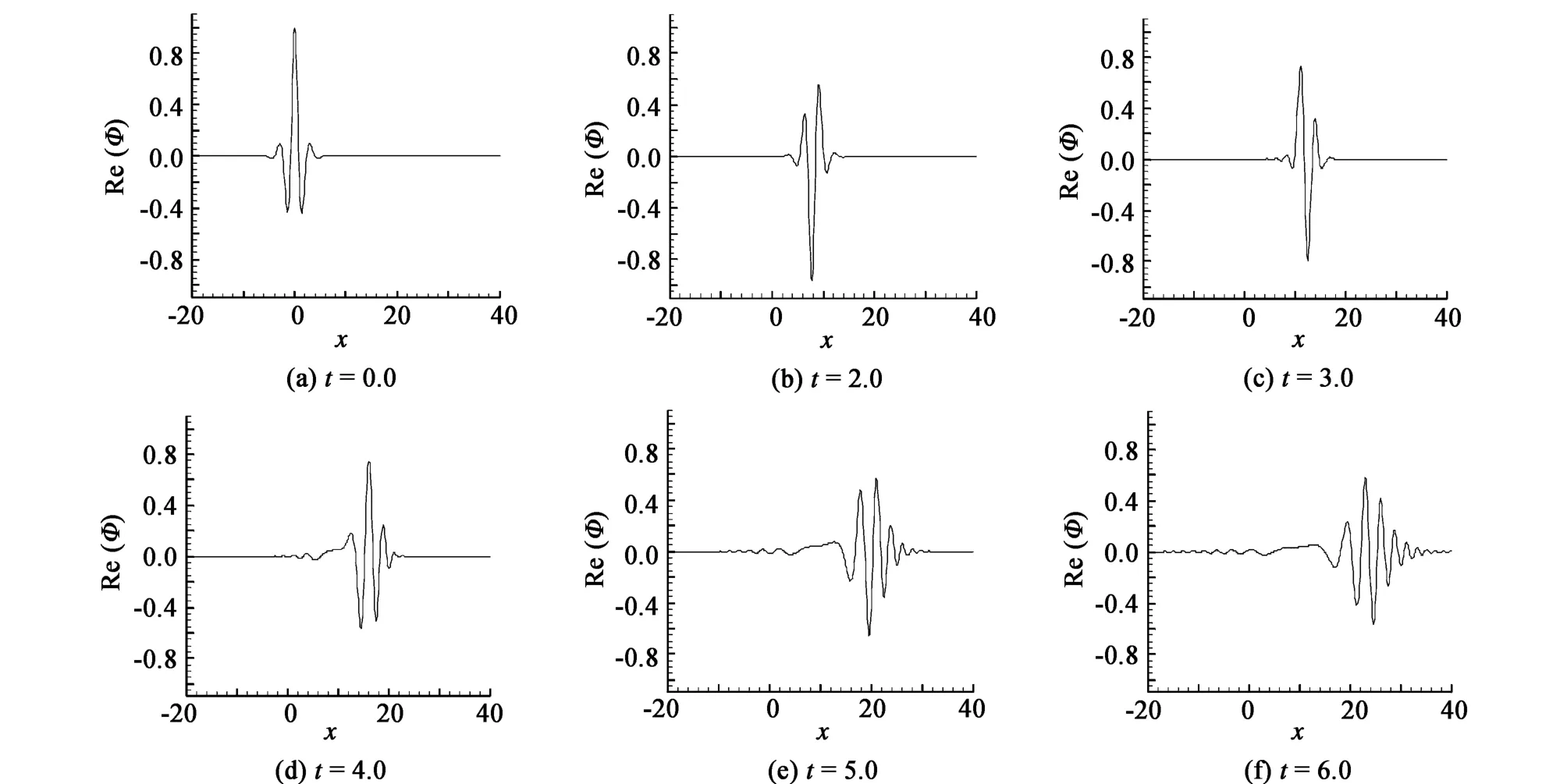
图4 不同时刻时孤立波的反射和透射Fig.4 The soliton′s reflection and transmission at different times
由图4可见,孤立波入射到一个界面时,在界面处会将一部分折返回原介质,在原介质形成一个反向行进的反射波,而另一部分透射到另一介质,在另一介质中沿原来的方向继续前进。由于反射波的能量耗散,相比于入射波,透射波的波幅减小。而透射波的波数相比于入射波增加,这是因为在介质的分界面上透射波发生了分裂。数值计算结果在物理上很好地解释了孤立波的传播,入射波分成了反射波和透射波,然后发生分裂的现象。
4 结 语
主要研究了局部微分求积法(LDQ法)对非线性薛定谔方程的孤立波解的数值求解。由于非线性孤立波在传播过程中始终保持稳定的速度和形状,对数值精度的要求很高。LDQ法采用局部节点处理的方法,计算精度高,计算量小,使其能够胜任对非线性孤立波的求解。
分别模拟了单深水孤立波运动,同向双深水孤立波追赶碰撞耦合运动,高阶孤立波振动和孤立波的反射与透射现象,并得到了较好的数值结果,展示了深水孤立波的一些奇妙特性和运动规律,分析了在不同初值条件下波形的变化特点,也验证了LDQ法对该类问题的有效性。
由于深水孤立波是一种非常复杂的非线性现象,此处只是一个初步的研究,在未来的工作中将致力于将1+1维的数值方法拓展到2+1维。
[1] 刘式适,刘式达.物理学中的非线性方程[M].北京:北京大学出版社,2001:214-217.
[2] Zhu Jia-min,Ma Zheng-yi,Fang Jian-ping,etal.General jacobian elliptic function expansionmethod and itsapplications[J].Chinese Physics,2004,13(6):798-804.
[3] 朱家民.高阶非线性薛定谔方程的精确解研究[J].激光与红外,2006,36(5):389-391.
[4] 王 伟,吴士明,孙建华.一般非线性schrödinger方程的显示孤立波解[J].应用数学学报,2004,27(2):282-290.
[5] 赵 磊,隋 展,朱启华,等.分步傅里叶法求解广义非线性薛定谔方程的改进及精度分析[J].物理学报,2009,58(7):4731-4737.
[6] 范恩贵,张鸿庆.非线性孤子方程的齐次平衡法[J].物理学报,1998,47(3):353-362.
[7] 阮航宇,李慧军.用推广的李群约化法求解非线性薛定谔方程[J].物理学报,2005,54(3):996-1001.
[8] Bellman R E,Casti J.Differential quadrature and long-term integration[J].Journalof Mathematical Analysisand Applications,1971,34:235-238.
[9] Zong Z,Lam K Y.A localized differential quadraturemethod and its application to the 2D wave equation[J].ComputationalMechanics,2002,29:382-391.
[10] 张义丰,李瑞杰,罗 锋,等.深水波浪非线性薛定谔方程及其精确解[J].水科学进展,2009,20(3):361-365.
[11] Zong Z,Zhang Y Y.Advanced Differential Quadrature Methods[M].New York:CRC Press,2009:241-255.
[12] 王振东.孤立波与孤立子[J].力学与实践,2005,27(5):86-88.
[13] 庞小峰.孤子物理学[M].成都:四川科学技术出版社,2003:168-169.
Numerical simulationsof deep-water envelope solitons using localized differential quadrature(LDQ)method
ZHANGNu,ZONG Zhi,YU Xin
(School of Naval Architecture Engineering,State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian Universityof Technology,Dalian 116024,China)
TV139.2
A
1005-9865(2011)01-0041-06
2010-04-21
创新研究群体科学基金资助项目(50921001);国家重点基础研究发展计划资助项目(2010CB83270)
张 弩(1984-)男,辽宁本溪人,博士生,主要从事船舶与海洋工程水动力性能计算研究。E-mail:zhangnu@yahoo.cn

