用两种不同方法计算淀山湖风浪

张洪生,文武键,辜俊波

(上海交通大学海洋工程国家重点实验室,上海 200240)

用两种不同方法计算淀山湖风浪

张洪生,文武键,辜俊波

(上海交通大学海洋工程国家重点实验室,上海 200240)

对淀山湖进行了风场和风浪场的现场观测。分别利用规范公式和SWAN模型计算了湖区风浪场的波高,并将计算结果和现场观测值进行了比较,比较说明两种方法的计算结果存在比较明显的差别。可为今后的相关工作提供借鉴和参考,并可为淀山湖的进一步治理积累必要的工作基础。

淀山湖;风浪;现场观测;规范公式;SWAN模型

Abstract:Wind field andwindwave field aremeasured in Dian-shan Lake.Windwave heights in Dian-shan Lake are calculated by the useof the normal formula and the SWANmodel,and they are comparedwith themeasured data,respectively.It is indicated thatobvious differences exist between the two different approaches.The research contentspresented in thispaper are beneficial to the relevant researchworks in the future.

Key words:Dian-shan Lake;wind wave;field measurement;normal formula;SWAN model

淀山湖属太湖流域,为平原浅水湖泊,呈东北～西南走向,南宽北窄,形似葫芦。其最大长度为14.5 km,最大宽度为8.1 km、平均宽度为4.3 km,岸线长为62.3 km,面积为63 km2。多年平均水位为2.63m,为平原浅水湖泊,具有风生浪起的特征[1]。在大风特别是台风作用下产生的风浪威胁着环湖大堤的安全运行;风浪对水流的作用通过辐射应力的形式表现出来,从而影响和改变水流的结构。因此,研究淀山湖的风浪对环湖大堤的规划和设计、对水质的评价都是十分重要的。

《堤防工程设计规范》(GB50286-98)[2]规定了计算内陆湖泊风浪要素的方法。该计算方法相对简单,但需假定湖区的水深和风场变化比较缓慢。但事实是湖区的水深并不一定缓慢变化,尤其是岸堤附近水深变化较大;风场随时空的变化也并不一定缓慢,尤其是遇到台风过程时,不同位置的风向可能有很大的不同。应用规范规定的方法计算内陆湖泊的风浪究竟存在多大误差,还需要进行进一步定量的研究。而且,该方法在计算单个工程位置的波要素时较为简单,但很难较快地计算出整个湖区在不同时刻的波要素。

SWAN(Simulating Waves Nearshore)模型[3]是荷兰Delft理工大学基于第三代风浪模式而建立的风浪数值模型,该模型综合考虑了波浪传播过程中水底地形的折射影响、波浪破碎、底摩擦、波波相互作用和白帽浪等多种因素的影响,是国际上比较通用的近岸风浪模型[4-8]。应用该模型可以得到在计算有效时间段内的任意时刻在任意位置(网格点)上的波要素。但该模型还较少应用于内陆湖泊风浪的数值模拟。虽然文献[9]利用该模型数值模拟了太湖的风浪,但并没有将计算结果与实测值的比较情况进行较为详细的分析讨论。相对于近岸水域,一般说来内陆湖泊的岸线更为曲折复杂,水深变化也更为剧烈。而SWAN模型存在着不能很好地模拟近边界处波浪场的缺点。这就需要探讨如何将该模型应用于内陆湖泊风浪的数值模拟。主要目的是在淀山湖水域分别根据《堤防工程设计规范》(GB50286-98)[2]和SWAN模型[3]两种方法计算湖区的风浪,并通过将计算结果和现场观测值进行比较,以观察两种方法计算结果的差别。

1 现场观测

1.1 观测位置及时间

在三个测点位置进行了现场测量,其中 1号站位的坐标为(120°55′29.9″,31°5′11.5″),2号站位的坐标为(120°56′50.1″,31°6′6.3″),3 号站位的坐标为(120°58′13.2″,31°7′22.1″) 。三个站位的示意见图 1。观测时间为2009年7月18日和21日两个白天。

1.2 观测设备

风浪观测仪器采用美国海鸟公司生产的浪潮仪SBE-26。该仪器适用的测量水深范围为0～21.0m、水温范围为-5℃～45℃;采样时间间隔为0.25 s,波高的分辨率为0.4mm。每20min观测一次,每次观测的持续时间为256 s或512 s,采样时间间隔为0.25 s。将浪潮仪悬吊在三角支架上,并沉入水下。

1.3 观测结果

三个站位风浪场和风场的测量结果分别见图2～4。由图2～4可见,在同一个时刻,湖中三个站位的波高并不相同,风场也不相同;而且它们的变化也并不完全同步。风浪场和风场并不同时变化的原因应当是:风浪场尽管是由风场所驱动产生的,但风浪场的变化应当比风场的变化存在时间滞后现象;风浪场的变化除受到风场的影响外还受到水深地形变化等因素的影响。

图1 淀山湖水域边界及各测点位置示意Fig.1 The sketch of the boundary of Dian-shan Lake and themeasurement locations

图2 现场观测的三个站位的有效波高Fig.2 Themeasured significantwave heights at three locations

2 风浪场的计算

2.1 利用规范公式计算风浪场

2.1.1 有效风区长度的计算公式

鉴于淀山湖水域的边界形状很不规则,需要引入有效风区长度的概念来进行波浪的计算。等效风区长度Fe的计算公式[2]:

式中:ri为主风向两侧各45°范围内、每隔Δa角由计算点引到对岸的射线长度(m);ai为射线ri与主风向上射线r0之间的夹角(度),ai=i×Δa。可取Δa=15°,i=0,±1,±2,±3。见图 5。

图3 现场观测的三个站位的风速Fig.3 Themeasured wind speeds at three locations

图4 现场观测的三个站位的风向Fig.4 Themeasured wind direction at three locations

2.1.2 有效波高的计算公式

鉴于淀山湖的长度仅为14.5 km,最大宽度8.1 km,因此,可不计入风时的影响。应用下式计算平均波

高[2]:

式中:¯H为平均波高(m);V为采用的计算风速(m/s),应为水面10m高度处的值;d为有效风区长度内的平均值(m);g为重力加速度(m/s2)。

根据

图5 等效风区长度计算Fig.5 The calculation chartof equivalent fetch length

可求得各点处的有效波高。

2.2 利用SWAN模型计算风浪场

2.2.1 SWAN模型的原理简介

SWAN模型[3]是根据风、底部和水流的条件对近海地区、湖泊和河口的波浪参数进行现实模拟的第三代波浪模型。该模型的控制方程是基于带有源、汇项的波作用平衡方程,其在直角坐标系下的表达形式:

式中 :N(σ,θ)=E(σ,θ)/σ,σ为相对频率,θ为波向,E(σ,θ)为能谱密度,N(σ,θ)为波作用量;cx、cy、cσ和cθ分别为波作用量在x方向、y方向、频率空间和波向空间中的传播速度;S代表物理过程所产生的源汇项。

模型主要考虑的物理过程是:地形影响所产生的折射和浅水变形、非线性的波波相互作用(包括浅水的三个一组和深水的四个一组相互作用)、水流引起的折射、障碍物透射、以及初步地考虑绕射作用。风浪的源、汇项主要包括:风能摄入、白帽浪的能量耗散、水深所引起的波浪破碎、底摩擦损耗等。模型能输出波高、波向和波浪引起的增水等诸多物理量。模型的优点是能够根据需要灵活选用所需要考虑的物理过程以及某一物理过程的不同参数化形式。

模型采用全隐式有限差分格式求解,无条件稳定,与采用显式有限差分格式的传统波浪谱模型相比,其时间步长可以取得更大,在用作波浪预报时增强了其时效性。

2.2.2 SWAN模型有关参数的选取

SWAN模型中包含有若干物理过程的处理,相应地含有不少计算参数。但模型手册强烈建议使用模型系数的缺省值。在数值计算淀山湖的风浪场时,也曾经对若干参数进行了调试,例如调试了底摩擦系数,但发现对计算结果的影响很小,当然,这有可能与计算的情况有关。鉴于该模型是一个得到较为广泛使用的模型,在数值计算淀山湖的风浪场时,对于物理过程的处理我们使用了SWAN模型建议的相关参数值。其它相关参数主要有:θ空间的网格数采用36,即谱方向的分辨率为10°;最小频率为0.08 Hz、最高频率为1.0 Hz。JONSWAP底摩擦公式的系数取为0.067 m2/s3。当波高的最大值与水深的比值为0.73时允许波浪破碎。数值求解格式采用一阶的空间和时间向后差分格式(BSBT),每个时间步的最大迭代次数选为3次。经测试表明,迭代次数选为3次是恰当的[10]。如迭代次数少于3次,有可能产生计算结果的不稳定;如迭代次数大于3次,则会徒劳地延长计算时间。

鉴于SWAN模型存在不能较好地模拟近岸处波浪场的缺点,所采用的计算范围比实际水域要大,如图6所示。经过模型试验,将包含整个湖区的计算域沿东西方向剖分为211个网格点,沿南北方向剖分为232个网格点,网格步长均取为100.0m。将读入点的水深插值到计算网格点上。采用如下公式进行插值:

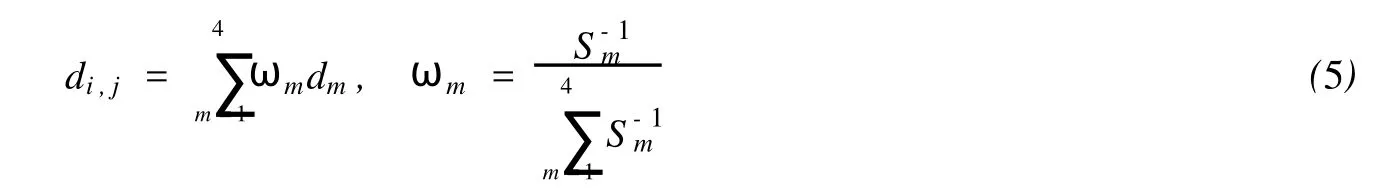
图6 湖底地形高程Fig.6 The elevation chart at Dian-shan Lake bed

式中:Sm为坐标点(i,j)周围距离最近的四个节点之一的第m个节点到坐标点(i,j)的距离,ωm为其权重,dm为第m个节点的水深,di,j为坐标点(i,j)处的水深。

2.3 有效波高的计算结果

考虑到各测点开始测量风场和风浪场的时刻不同,将风场和风浪场的观测结果都统一到整点时刻,并统一从09∶00时开始计算湖区的风浪场。曾经在计算范围为40 km×40 km的水域就风速10m/s的情况,探讨了利用非恒稳模式进行计算时,波高随时间的变化过程。结果发现,在100分钟后,所计算的波高和稳态模式的计算结果接近[10]。文献[9]在基于SWAN模型的非稳态模式计算太湖水域的波浪时,通过假定不同的风速也探讨了波高随时间变化的特点。发现在风速为5m/s的时候,波浪发展到稳定需120～150min。鉴于淀山湖的水域面积远远小于太湖(太湖的水域面积为2 338.11 km2),在模型运行一小时后,即从10∶00开始输出计算结果是完全可行的。计算结果见表1～3。

表1 1号观测站的风浪观测资料与计算结果比较Tab.1 The comparison of the calculated wave heights with themeasured data at Location 1

表2 2号观测站的风浪观测资料与计算结果比较Tab.2 The comparison of the calculated wave heights with themeasured data at Location 2

表3 3号观测站的风浪观测资料与计算结果比较Tab.3 The comparison of the calculated wave heights with themeasured data at Location 3

3 不同方法计算结果的比较

为了便于比较,将观测值插值到整点时刻。表1～3为观测的有效波高、利用经验公式计算的有效波高和利用SWAN模型计算的有效波高的详细比较。由表1可见,在7月18日1号站位根据规范公式计算的有效波高的绝对误差为0.06m、相对误差为33.27%,根据SWAN模型计算的有效波高的绝对误差为0.04 m、相对误差为19.81%;在7月21日根据规范公式计算的有效波高的绝对误差为0.02m、相对误差为16.39%,根据SWAN模型计算的有效波高的绝对误差为0.03m、相对误差为20.82%;两天内利用规范公式计算的有效波高的平均绝对误差为0.04m、相对误差为24.83%,利用SWAN模型计算的有效波高的平均绝对误差为0.03m、相对误差为20.32%。由表2可见,在7月18日2号站位根据规范公式计算的有效波高的绝对误差为0.08m、相对误差为38.87%,根据SWAN模型计算的有效波高的绝对误差为0.06m、相对误差为25.12%;在7月21日根据规范公式计算的有效波高的绝对误差为0.06m、相对误差为31.92%,根据SWAN模型计算的有效波高的绝对误差为0.06m、相对误差为29.87%;两天内利用规范公式计算的有效波高的平均绝对误差为0.07m、相对误差为35.39%,利用SWAN模型计算的有效波高的平均绝对误差为0.06m、相对误差为27.49%。由表3可见,在7月18日3号站位根据规范公式计算的有效波高的绝对误差为0.11 m、相对误差为37.88%,根据SWAN模型计算的有效波高的绝对误差为0.08m、相对误差为26.36%;在7月21日根据规范公式计算的有效波高的绝对误差为0.05m、相对误差为26.81%,根据SWAN模型计算的有效波高的绝对误差为0.04m、相对误差为21.29%;两天内利用规范公式计算的有效波高的平均绝对误差为0.08 m、相对误差为32.35%,利用SWAN模型计算的有效波高的平均绝对误差为0.06 m,相对误差为23.97%。两天内利用规范公式计算的各站位的平均绝对误差为0.06m,相对误差为30.86%;两天内利用SWAN模型计算的各站位的平均绝对误差为0.05m,相对误差为23.93%。因此,很明显SWAN模型的计算精度要高于经验公式的计算精度。

为了进一步定量地探讨利用不同方法所得计算结果的精度,采用公式[11]:

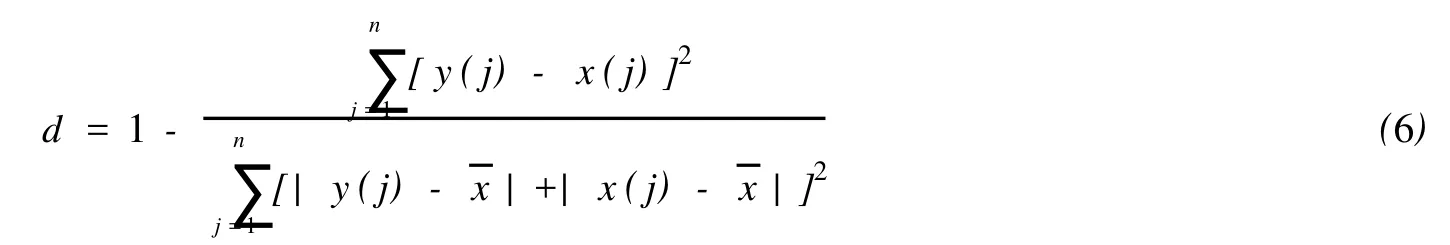
进行定量地比较。其中,x(j)为标准值(此处为现场观测值),¯x为x(j)的平均值,y(j)为计算值。当d=0时代表二者完全失配;当d=1时代表二者完全一致。

利用不同方法所得计算结果与现场观测值的一致程度比较见表4。在观测的两天内,对于三个站位,根据SWAN模型的数值解统计的d的平均值是0.360 4,根据规范公式的计算结果统计的d的平均值是0.367 1。从两天的统计平均值,不能看出利用不同方法所得计算结果的明显差别。但从表4可见,利用规范公式所得计算结果与现场观测值的符合程度在不同的时间和站点存在着时好时坏的现象,而根据SWAN模型所得计算结果与现场观测值的符合程度相对来说要均匀些。初步认为产生这种现象的原因是:规范公式是在对大量的观测结果进行统计分析的基础上得到的,这样利用规范公式进行计算所得到的结果就有可能出现前后不一的情况;而SWAN模型是根据波作用量守恒的原理,进行数值计算求解得到计算结果,因此,利用该模型所得计算结果会比较稳定。对于产生差别的原因,在我们将来的工作中将继续进行研究和分析。

表4 以现场观测值作为 x(j)、以不同方法的计算结果作为 y(j)计算的 dTab.4 The calculated index d with field data as x(j)and calculated resultsas y(j)

图7～8为有效波高的观测结果、经验公式计算结果和SWAN模型的计算结果的比较。从图7和8可见,从定性上看,无论是经验公式的计算结果还是SWAN模型的计算结果都和实测波高的变化趋势基本一致。由于我们的观测时间只有两天,在观测的时间段内风速也不大,因此,对于两种方法所计算波高的精度还需要更为详细的研究。

图7 2009年07月18日的波高计算结果与实测结果的比较Fig.7 The comparison of calculated wave heightswith themeasured data on July 18,2009

图8 2009年07月21日10时开始的波高计算结果与实测结果的比较Fig.8 The comparison of calculated wave heightswith themeasured data on July 21,2009

4 结 语

通过分别和淀山湖三个站点的波高的观测资料进行比较,发现基于SWAN模型所计算的波高的平均误差比基于规范公式所计算的波高的平均误差要小。利用规范公式所得计算结果与现场观测值的符合程度在不同的时间和站点存在着时好时坏的现象,而根据SWAN模型所得计算结果与现场观测值的符合程度相对来说要均匀些。两种方法计算波高的精度尚需进一步的研究和讨论。此处的工作还是初步的,这是因为:由于客观条件的限制,我们仅进行了两天的观测;由此,我们也就仅进行了两天的风浪场的比较;进行观测时,风力较弱,即风速不大,在大风尤其是台风天气条件下,二者的计算精度如何尚需进一步的比较判断。

讨论了两种方法计算结果的区别及其产生的原因,为今后的相关工作提供了借鉴和参考。同时,此处的工作成果可为淀山湖的进一步治理积累必要的工作基础。

[1] 张洪生,文武健.淀山湖堤防规划设计波浪爬高的研究[R].上海:上海交通大学,2009.

[2] GB50286-98,堤防工程设计规范[S].北京:中国水利水电出版社,1999.

[3] The SWAN team.SWAN Technical documentation[R].Delft University of Technology,2007.

[4] Booij N,Ris R C,Holthuijsen L H.A third-generationwavemodel for coastal regions1:model description and validation[J].Journal of Geophysical Research,1999,104(C4):7649-7666.

[5] Ris R C,Holthuijsen L H,Booij N.A third-generation wavemodel for coastal regions2:verification[J].Journal of Geophysical Research,1999,104(C4):7667-7681.

[6] 徐福敏,张长宽,茅丽华,等.一种浅水波浪数值模型的应用[J].水动力学研究与进展:A辑,2000,15(4):429-434.

[7] Lin W Q,Sanford L P,Suttles SE.Wavemeasurement andmodeling in Chesapeake Bay[J].Continental Shelf Research,2002,22:2673-2686.

[8] Ou SH,Liau JM,Hsu TW,et al.Simulating typhoonwaves by SWANwavemodel in coastalwatersof Taiwan[J].Ocean Engineering,2002,29:947-971.

[9] 李一平,逢 勇,刘兴平,等.太湖波浪数值模拟[J].湖泊科学,2008,20(1):117-122.

[10] 张洪生,于小伟,周华伟,等.太湖风浪预测系统应急完善技术报告[R].上海:上海交通大学,2009.

[11] ZHANG Hong-sheng,ZHU Liang-sheng,YOU Yun-xiang.A numerical model for wave propagation in curvilinear coordinate[J].Coastal Engineering,2005,52:513-533.

Calculation of wave heights in Dian-shan Lakewith two approaches

ZHANG Hong-sheng,WENWu-jian,GU Jun-bo
(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

TV148

A

1005-9865(2011)01-0122-08

2010-08-02

国家自然科学基金资助项目(40676053,51079082);上海市科学技术委员会资助项目 (08DZ1203005);上海交通大学海洋工程国家重点实验室资助项目(GKZD010012,GK2D010024)

张洪生(1967-),男,山东高唐人,副教授,从事水波动力学的理论及其应用研究。E-mail:hhszhang@sjtu.edu.cn