大长细比柔性杆件涡激振动实验

唐国强,吕 林,2,滕 斌,谢 彬,宋吉宁,张建侨,吴 浩

(1.大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024;2.大连理工大学深海工程研究中心,辽宁 大连 116024;3.中海石油研究中心技术研究部,北京 100027;4.中国水产科学研究院渔业工程研究所,北京 100141)

大长细比柔性杆件涡激振动实验

唐国强1,吕 林1,2,滕 斌1,谢 彬3,宋吉宁1,张建侨4,吴 浩1

(1.大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024;2.大连理工大学深海工程研究中心,辽宁 大连 116024;3.中海石油研究中心技术研究部,北京 100027;4.中国水产科学研究院渔业工程研究所,北京 100141)

涡激振动(vortex-induced vibration,VIV)是导致深海细长柔性立管发生疲劳破坏的重要因素。采用实验观测手段研究了长细比为1 750的柔性立管多模态涡激振动特性。实验中,通过采用拖车拖拉立管模型在水池中匀速行进来模拟均匀流作用下的涡激振动响应。利用光纤光栅传感器测量立管模型在横流向(cross-flow,CF)和顺流向(in-line,IL)的应变,进而通过模态分解的方法,获得立管模型涡激振动的位移。在此基础上,研究了CF以及IL方向的响应频率、位移标准差的平均值和最大值等随流速的变化规律,并分析了立管模型上测点的运动轨迹及其影响因素。

细长柔性立管;涡激振动;动力响应;模态分解

Abstract:Vortex-induced vibration(VIV)isoneof themost important factorsaccounted for the fatigue damageof long-flexible risers in deep water.Laboratory testswere conducted to investigate themulti-mode dynamic responsesof risermodel subjected to steady current flow.The risermodel is28m in length and 1.6 cm in diameter,leading to a large aspect ration of 1750.The risermodelwas installed on a towing carriage,whichmightmove horizontally above awave basin with desirable speeds.Thus a uniform current could bemodeled in a straightforward manner.The strainof risermodel in both Cross-flow and In-line directionswas recorded by the Fiber Bragg Grating(FBG)sensorsand the displacementswere obtained bymeansof themodal decomposition method.The variationsof frequency spectrum and standard deviation of displacementwith towing speedwere examined.Theorbitalmotionof typical cross-sectionof the risermodel and its dependencewere also investigated.

Key words:long-flexible riser;vortex-induced vibration(VIV);dynamic response;modal analysis

海洋立管是连接上部平台和海底井口的重要海洋工程设施。在深海环境下,立管结构往往具有很大的长细比,此时所承受的海洋环境荷载主要是水流的作用。当水流经过立管时,会在其两侧形成交替的漩涡脱落,由此产生的周期性作用力会引起立管的涡激振动现象(vortex-induced vibration,VIV)。当立管的固有频率与涡旋的脱落频率比较接近时,会发生“锁定”(Lock-in)现象。“锁定”的发生将导致立管的疲劳寿命急剧降低;同时,由于拖曳力的相应增加,也会加剧立管的断裂破坏等,从而造成严重的经济损失和环境污染。

近年来,国内外许多学者针对深海细长柔性立管涡激振动的动力响应问题进行了模型实验和数值分析工作。模型实验基本可分为室内实验和现场测试两大类,前者主要集中于刚性圆柱的自由振动和受迫振动,后者主要针对细长柔性结构。而数值方面的研究工作,主要集中在CFD模型[1-2]以及经验模型[3-4]两大类。CFD模型由于计算量较大的缘故,还难以直接应用到实际的海洋工程问题中。因此,立管涡激振动的数值分析目前仍主要依赖于经验模型。以Vandiver[3]和Larsen[4]等为代表的学者分别开发了可用于实际工程问题的经验分析模型,用于分析海洋石油平台立管的涡激振动动力响应问题。由于立管涡激振动现象的复杂性,以及这些模型建立的基础主要依据室内刚性圆柱的受迫振动实验资料,因此这些经验模型对深海细长柔性结构涡激振动的预报还难以达到令人满意的程度。由于海洋立管的长细一般比较大,涡激振动发生时能够激发出更多的模态共同参与,并且模态之间的频率间隔很小,涡激振动引起的立管动力响应往往具有多模态共同参与的随机振动特点,这些现象难以通过简化的刚性圆柱物理模型实验来模拟。因此,有必要开展大长细比情况下深海立管的涡激振动物理模型实验,以更加深入的理解和认识涡激振动的物理现象,为经验模型的发展提供更为可靠的数据资料。Vandiver[5-7]利用野外环境开展了细长柔性立管涡激振动的现场实验,他们在实验中重点观测了拖曳力随流速的变化规律,并进行了CF和IL两个方向的振动耦合分析。但是由于野外现场环境的影响因素复杂,水流速度沿着立管轴向的分布难以确定,因此实验的测量结果难以用于涡激振动经验模型和CFD模型的校验。Trim[8]等通过室内水池拖拉方式开展了长度为38 m的柔性立管涡激振动实验,主要研究了螺旋条纹涡激振动抑制措施的效果,并针对该抑制措施计算了立管的疲劳寿命。Tognarelli[9]研究了立管在均匀流以及剪切流情况下的涡激振动问题。以上两项实验工作都采用了加速度传感器来进行涡激振动响应信号的观测,由于加速度传感器体积和质量较大,因此它们对局部流场和结构特性都会产生比较明显的影响作用。此外,Chaplin等[10]还通过室内实验研究了立管在阶梯流作用下的动力响应问题,得到了各个模态的响应情况。

目前,国内开展细长柔性立管涡激振动的实验还很少。张建侨等[11]利用波浪水槽研究了质量比对立管模型涡激振动响应的影响作用,但立管模型的长度非常有限。在此基础上,宋吉宁等[12]进一步研究了利用三根附属控制杆来抑制涡激振动的效果。为适应我国目前加速进行深海油气资源勘探、开发的迫切需要,近期在大连理工大学海岸和近海工程国家重点实验室多功能综合波浪水池中进行了长细比为1 750的立管模型涡激振动实验。其目的在于:1)加深对细长柔性立管涡激振动物理现象的认识;2)为实际的海洋石油平台立管设计提供技术参考;3)为数值模型的建立和发展提供更为可靠和有效的数据资料。

1 实验设置

1.1 实验水池

实验水池的尺寸为55 m×34 m×0.7 m(长×宽×深),立管模型的中心距离水面0.4 m。相关的数值计算表明[13],对于圆柱扰流问题,当流场趋于稳定后,圆柱后方的尾涡影响范围相当有限,基本在5倍的管径范围内,因此水深可以满足实验的要求。水池的上部建有拖车系统,通过变频电机驱动,可以在滑轨上进行平稳的往复水平运动。在本次实验中,由于立管模型的质量比为1.0,因此重力的影响十分有限,实验的结果与垂直放置的立管实验没有本质的差别。本实验采取拖车拖拉的方式进行涡激振动实验,因此可对相对流速进行准确控制。实验中拖车运行速度范围为0.15 m/s到0.6 m/s,通过采用变频器控制电机转速来设定拖车的运行速度,拖车速度的变化间隔为0.015 m/s。图1与图2以及图3分别为实验装置的示意图,现场图片和端部张力系统示意图。

图1 整体实验示意Fig.1 Sketch definition of the experimental setup

图2 实验现场图片Fig.2 Photograph in the laboratory test

图3 端部张力系统Fig.3 Spring tension system

1.2 立管模型

立管的模型采用钢管,长度为28.04 m,外径为0.016m,长细比为1 750。两端采用铰接的方式连接在拖车上(一端与拖车支架直接相连,另一端连接滑块-弹簧系统,便于施加预张力,同时允许发生轴向运动)。立管的详细模型参数如表1所示。

实验的过程中,立管模型由于水流的作用会产生很大的静变形,如果静变形过大,会对传感器造成损坏。在本次实验中,需要将立管在水流作用下的静变形控制在1 m之内。在实验开始之前,利用Morison公式初步的估计了立管模型在不同的初始张力情况下可能产生的最大静变形,并综合考虑了涡激振动过程中的拖曳力放大现象,选取了表1中的三组张力作为初始的张力。

表1 立管的模型参数Tab.1 Properties of the riser model

1.3 实验工况设计以及数据采集

实验中利用光纤光栅应变传感器进行应变监测和采集。光纤光栅应变传感器的直径仅有0.3mm,因此对流场的扰动很小,同时光纤光栅应变传感器还具有不受电磁信号干扰,不需要进行防水处理等优点,所以特别适合小直径柔性立管涡激振动实验。

在开展涡激振动实验之前,沿立管模型轴向等间隔布置了14个应变测点,每个测点位置有4个光纤光栅传感器,它们对称布置在立管模型的垂直和水平外表面,即采用90度等角度方式布置,如图4所示,实验中的传感器采用了封装技术进行了处理。实验过程中,立管施加了预张力,并且由于水流的作用,端部的张力是脉动变化的,从而引起光纤光栅传感器波长的变化。这部分波长的变化所对应的应变并不是由于涡激振动引起的,因此在数据处理的时候必须将其剔除。假设某一传感器由于张力引起的应变为a,由涡激振动引起的应变为b,那么其对称面由于涡激振动引起的应变为-b。对于对称的两个传感器,总的应变分别为a+b和a-b,将两个对称的传感器总的应变值进行相减并除以2,便可以消除脉动张力的影响。实验中所采用的光纤光栅传感器的采样频率为250 Hz。

1.4 实验数据处理方法

针对以上实验设置方案,建立如图5所示的坐标系统,坐标原点坐于立管模型的左端点,x坐标轴指向拖车水平行进方向,对应IL的方向,y坐标轴垂直向上,对应CF方向,z方向为立管模型的轴向。

以y方向的振动为例,对于长度为L的立管振动问题,应用模态叠加方法可将立管振动位移y(z,t)表示为[14]

式中:z为立管的轴向坐标,t为时间,ωn(t)为权重函数,φn(z)为模态函数,n为立管的振动模态,L为立管的总长度。

对于两端铰接的立管,其模态函数可以表示为

应该说明的是,在本实验中虽然左端允许轴向的自由滑动,但限制了沿坐标轴y方向的运动以及扭转,因此该端也可以近似为铰接的边界条件形式。那么,立管各点的位移及位移的二阶导数分别为

式中:ε(t,z)为测量的应变信号,R为立管半径。

图4 传感器布置示意Fig.4 Schematic of sensorson the risermodel

图5 立管坐标系统示意Fig.5 Schematic definition of coordinate system

通过式(5),可以计算得到每个测点模态权重函数ωn(t)的时间过程线。将ωn(t)代入式(3)中,即可得到立管模型上每个测点的位移时间过程线。

2 实验结果及分析

2.1 位移以及频谱分析

图6以及图7分别为测点位于z/L=0.33,流速为0.345 m/s时CF以及 IL方向的位移和频谱分析结果。其中y/D和x/D表示CF以及IL方向的无因次位移,Ay/D以及Ax/D表示CF和IL方向的无因次振幅,D为立管模型直径。

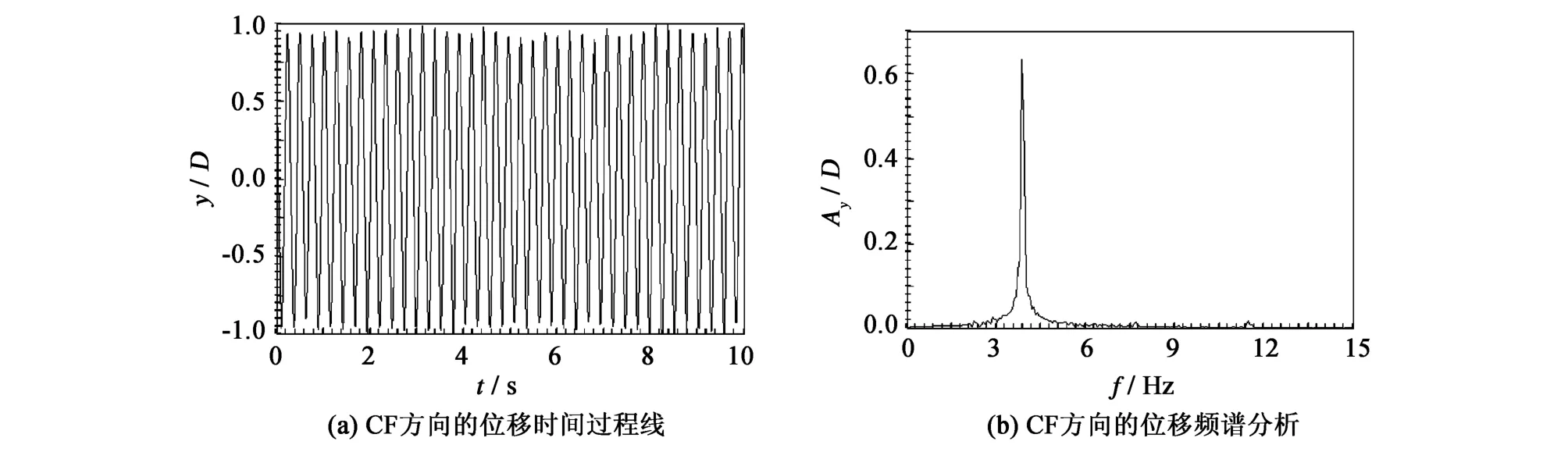
图6 CF方向的位移时间历程以及频谱分析结果Fig.6 Time history of CF displacement and frequency spectrum analysis

图7 IL方向的位移时间历程以及频谱Fig.7 Time history of IL displacement and frequency spectrum analysis

比较图6和图7的位移时间过程线可以看出,IL方向的位移比CF方向小很多。但从频谱分析中可以看出,IL方向的振动频率是CF方向的2倍。尽管IL方向的位移很小,但其所具有的高频振动响应特性对立管的安全稳定是十分不利的,因此有必要研究IL方向的振动对于疲劳寿命的影响。

立管的涡激振动过程往往会有多个频率共同参与,但其振动会主要受到某一阶模态的控制,其它模态对于立管整体的振动影响很小。因此,立管的疲劳寿命也主要由其主导模态的控制,其它模态对于疲劳的影响相比于主导模态为小量。基于这一假设,对于两端铰接的立管模型,无论CF方向还是IL方向,其模态函数都可以写成如下的形式[15]

式中:n为立管振动的模态阶次,L为立管的总长度,an为立管的模态振幅。

立管的应力振幅表达式为

式中:M为立管所承受的弯矩,D为立管的直径,I为立管的截面惯性矩。

弯矩的表达式为

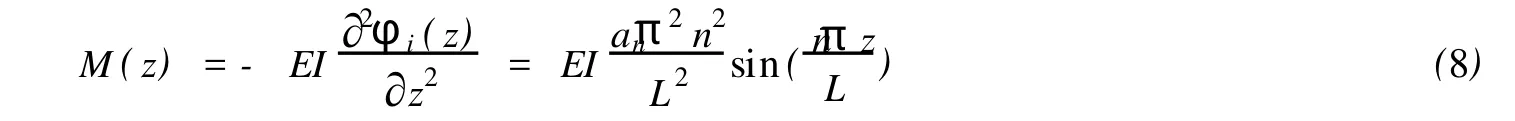
将式(8)代入到式(7)中,可以得到最大的应力振幅沿着立管轴向的空间分布为

那么,IL方向与CF方向应力振幅的比值为

从式(10)中可以看出,尽管CF方向的振幅通常较大,但由于IL方向的振动频率是CF方向的2倍,因此,从综合效果上考虑IL方向对于立管疲劳破坏的贡献是不容忽视的。

在以往的涡激振动研究工作中,人们往往更加关注CF方向的疲劳破坏程度而忽略了IL方向的分析工作。利用式(10)可以计算出IL方向与CF方向应力振幅的比值,进而可以研究IL方向的振动对疲劳破坏的影响程度。图8以相对流速为0.315m/s为例,给出了IL方向与CF方向应力振幅之比的空间分布。从图8可以看出,在5个测点上IL方向的应力振幅大于CF方向,并且最大的比值达到了3.5倍,其对于疲劳破坏的程度远高于CF方向。图9为立管模型中间点的IL方向与CF方向应力振幅比值随相对流速的变化规律。从图9的分析中可以看出,IL方向仍然有约25%的流速点其IL方向的应力振幅高于CF方向。从以上的分析结果中可以发现,IL方向振动对柔性立管涡激振动疲劳破坏的贡献应引起足够的重视。

立管上所有测点的振动位移随时间的变化可以清楚反映出立管振动的模态信息。图10(a)给出了端部张力为700 N,拖车速度为0.3m/s时,立管模型CF方向各测点位移在不同时刻的分布情况。图10(b)则对应端部张力为800 N和拖车速度为0.315 m/s的情况。图中各位移分布线所对应的时间为0.004 s到16.16 s,间隔为0.16 s。从图10中可以发现,在以上工况下,CF和IL方向的位移响应均为单一模态占主导的振动。实际的柔性立管在振动的过程中,除了主导模态以外,往往还会有其它的模态同时参与振动,但是这些模态贡献一般较小,通常不会在根本上改变位移响应的总体空间分布形状,但会引起图10和图11中位移沿空间分布的不对称性以及相位差。

图8 拖速为0.315m/s时IL与CF方向应力振幅比的空间分布Fig.8 The space distribution of the stress ratio of IL and CF direction at towing speed 0.315 m/s

图9 不同拖车速度下中间点IL方向与CF方向的应力振幅比Fig.9 The stress ratio for IL and CF direction in themiddle point at different towing speeds

图10 横向位移响应Fig.10 Cross-flow deflections

图11 顺流向位移响应Fig.11 In-line deflections

从图10和图11的比较中还可以看出,在两种工况下CF方向的参与模态均是4模态控制,而IL方向的主导模态为8模态。虽然,CF方向的位移响应明显大于IL方向,而IL方向的振动由于是在8模态的主导作用下,所以其振动频率也将明显高于CF方向。因此,从总体上而言,IL方向振动响应作用在柔性立管的整体的疲劳破坏中应占有相当大的比重。

2.2 位移标准差平均值以及最大值分析

图12和图13给出了CF以及IL方向位移标准差的平均值以及位移标准差的最大值随流速的变化情况。从图中可以看出,位移的变化趋势基本上是随着流速的增大缓慢增加。试验结果同时也表明,IL方向的位移响应约为CF方向的25%左右。

图12 位移标准差平均值随流速的变化Fig.12 Variation ofmean standard deviation of displacementwith towing speed

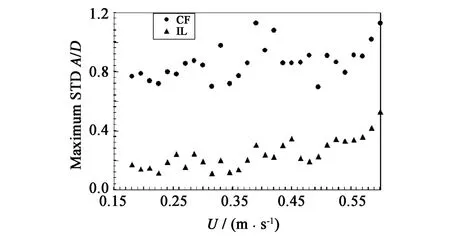
图13 位移标准差最大值随流速的变化Fig.13 Maximum displacement standard deviation vs.towing speed

2.3 立管测点运动轨迹分析

图14和图15以拖车速度为0.345 m/s为例,分别给出了奇数测点以及偶数测点位置的运动轨迹。

图14 奇数测点的运动轨迹Fig.14 Orbitalmotion of oddmeasurement points

图15 偶数测点的运动轨迹Fig.15 Orbitalmotion of evenmeasurement points

从图中可以看出,即使在同一个流速下,立管各个测点的运动轨迹也存在着很大的差别。这主要是由CF方向和IL方向位移的振幅分布以及二者之间的相位差造成的。测点位置的不同,导致CF以及IL方向振动幅值的不同,从而决定了运动轨迹的范围;在振动的过程中,由于CF方向和IL方向所存在的相位差,导致了运动轨迹形状的变化。

图16 CF以及IL方向的控制模态随雷诺数的变化Fig.16 The dominantmode for cross-flow and in-line versus Reynolds number

2.4 控制模态

涡激振动实验过程中,随着流速的增加,激发的模态阶次也会随着发生相应的改变。图16为CF以及IL方向的控制模态随雷诺数Re的变化。

从图中可以看出,随着雷诺数的增大,CF以及 IL方向的控制模态都是逐渐增大的趋势,并且IL方向的控制模态为CF方向的2倍。在振动的过程中,CF以及IL方向都存在同步的模态竞争现象。即随着雷诺数的增加,激发的模态阶次没有增加,反而降低。这种现象说明,涡激振动过程中往往伴随着复杂的流体与结构相互作用,立管的振动系统通过不断的调整附加质量以达到能量输入和能量消耗的动态平衡。

3 结 语

研究长细比为1 750的模型立管,在均匀流作用下的涡激振动问题。通过分析不同流速下的CF以及IL方向的位移响应、频率、位移标准差的平均值以及最大值和立管所有测点的运动轨迹,可以得出:

1)从测点的频谱分析可以看出,对单模态占主导地位的涡激振动,IL方向的主导频率为CF方向的2倍。但从位移的对比可以看出,IL方向的位移比CF方向的位移小很多。尽管IL方向的位移响应很小,但是IL方向和CF方向对于疲劳破坏的贡献基本处于一个数量级,甚至会高于CF方向的疲劳破坏程度。

2)从位移标准差的平均值以及最大值的分析中可以看出,CF以及IL方向的位移响应随着流速的增大而缓慢增加。IL方向的位移响应大概是CF方向的25%左右。

3)立管模型上不同测点的运动轨迹存在很大的差别,这主要是由各测点在CF和IL方向位移振幅不同,并且二者之间存在相位差所引起的。

4)在涡激振动的过程中,CF以及IL方向都存在着同步的模态竞争现象,反映出复杂的流体与固体相互作用的非线性关系。

[1] Meneghini J R,Bearman PW.Numerical simulation of high amplitude oscillatory flow about a circular cylinder[J].Journal of Fluid Structure,1995,9(4):435-455.

[2] Dong S,Karniadakis G E.DNSof flow past a stationary and oscillating rigid cylinder at Re=10 000[J].Journal of Fluid Structure,2005,20(4):519-531.

[3] Vandiver J K.SHEAR7 V4.3 Program Theoretical Manual[R].Massachusetts Institute of Technology,2003.

[4] Larsen CM,Vikestad K,Yttervik R,et al.VIVANA Theory Manual[M].Norway:MARINTEK,2001.

[5] Jong J Y,Vandiver J K.Response analysisof the flow-induced vibration of flexible cylinders tested at Castine[R].Massachusetts Institute of Technology,1983.

[6] Vandiver J K.Drag coefficientsof long flexible cylinders[C]∥Proc.Offshore Technology Conference.Houston:OTC4490,1983:405-414.

[7] Vandiver J K,Jone J Y.The relationship between In-Line and Cross-Flow vortex-induced vibration of cylinders[J].Journalof Fluid and Structure,1987,1(4):381-399.

[8] Trim A D,Braaten H,Lie H,et al.Experimental investigation of vortex-induced vibration of longmarine risers[J].Journal of Fluid and Structure,2005,21(3):335-361.

[9] TognarelliM A,Slocum S T,Frank W R,et al.VIV response of a long flexible cylinder in uniform and linearly sheared currents[C]∥Proc.Offshore Technology Conference.Houston:OTC16338,2004.

[10] Chaplin JR,Bearman PW,Cheng Y,etal.Blind predictionsof laboratorymeasurementsof vortex-induced vibrationsof a tension riser[J].Journal of Fluid and Structure,2005,21(1):25-40.

[11] 张建侨,宋吉宁,吕 林,等.质量比对柔性立管涡激振动影响的实验研究[J].海洋工程,2009,27(4):38-44.

[12] 宋吉宁,吕 林,张建侨,等.三根附属控制杆对海洋立管涡激振动抑制作用的实验研究[J].海洋工程,2009,27(3):23-29.

[13] 吕 林.海洋工程中小尺度物体的相关水动力数值计算[D].大连:大连理工大学,2006.

[14] 张建桥,宋吉宁,吕 林,等.柔性立管涡激振动实验的数据分析[J].中国海洋平台,2009,24(4):26-32.

[15] Vikestad K.Multi-frequency responseof a cylinder subjected to vortex shedding and supportmotions[D].Norwegian University of Science and Technology,1998.

Laboratorymeasurement of vortex-induced vibration of long flexible riser

TANG Guo-qiang1,LV Lin1,2,TENGBin1,XIEBin3,SONGJi-ning1,ZHANGJian-qiao4,WU Hao1
(1.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China;2.Center for Deepwater Engineering,Dalian Universityof Technology,Dalian 116024,China;3.CNOOCResearch Center,Beijing 100027,China;4.Fishery Engineering Research Institute of Chinese Academy of Fishery Sciences,Beijing 100141,China)

P751

A

1005-9865(2011)01-0018-08

2010-02-04

国家863计划资助项目(2006AA09A103);国家自然科学基金资助项目(50921001);海岸和近海工程国家重点实验室开放基金资助项目(LP0904)

唐国强(1982-),男,辽宁大连人,博士生,主要从事立管涡激振动方面的研究工作。E-mail:TangGQ@mail.dlut.edu.cn