液态金属棒束传热的理论分析

马在勇，仇子铖，王 美，田文喜，苏光辉，秋穗正

（西安交通大学 能源与动力工程学院，陕西 西安 710049）

核能发展到今天，快堆由于众多的优良特性越来越受到人们的重视。在第4代反应堆的6种候选堆型中，有3种是快堆，而这3种快堆中，又有2种使用液态金属作为冷却剂。研究液态金属的传热对于快堆的设计、运行和安全均具有十分重要的意义。液态金属具有很高的导热性和低的普朗特数，这使得其传热特性与普通流体很不相同，已有的普通流体的传热关系式不再适用，必须研究新的换热关系式。现有文献可查的液态金属棒束传热关系式很多，这些关系式主要由实验数据拟合而得，应用时具有一定的局限性。也有研究者通过建立模型和程序计算给出，但与实验结果相差颇大。

本工作通过建立模型和引入适当修正，研究新的液态金属棒束传热关系，并与实验结果进行比较。

1 模型建立

图1示出了三角形布置棒束的几何特征。填充区域即为本工作设定的基本传热单元，由6个通常定义的传热单元所组成。该传热单元外侧边界是等边六边形，与圆形非常相近，为方便处理，可将其近似为一同心环管，内径为r1，外径为r2。按面积相等的原则，可得到等效环管外径req的计算式。

图1 棒束传热模型Fig.1 Schematic of heat transfer model for tube bundles

图1中，六边形边长a＝P，其面积Aeq为：

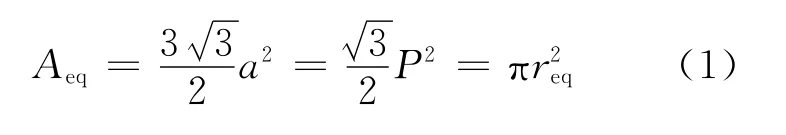
解得：

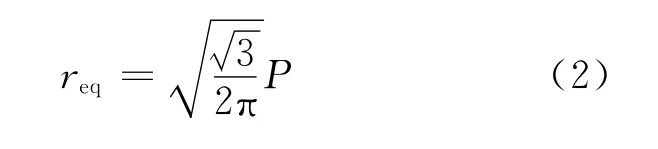
等效环管的径比yeq与节径比x的关系为：

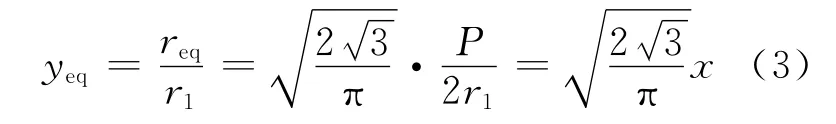
至此，完成将棒束传热向同心环管传热转变的第1步，类似的处理方式可参见文献［1－2］。在进行下一步工作前，首先分析该等效环管的流动传热特点，其特点如下。

1）该等效环管的充分发展流体速度分布与通常独立同心环管流体速度分布不同，其内径处是常规的无滑移条件，外径处则对应速度的最大值，同时，由于棒束之间的互相影响，其速度分布沿周向的变化也较大。

2）该等效环管内侧是等热流边界条件，外侧则可类似为绝热条件（对称性），同样由于棒束之间的相互影响，其温度分布沿径向和周向均有较大变化。

从上述分析可见，棒束之间的相互影响使等效环管的流动和传热特性变得相当复杂，难以分析。若不考虑棒束之间的相互影响，该等效环管的流动和传热特性则大为简化。在此，作出如下假设。

1）棒束之间的相互影响可简单地视为一几何效应，其对流动传热的整体影响可引入几何相关的修正项修正。引入该项修正后，可认为等效环管的截面速度、温度分布仅是径向的函数，与周向无关。

2）在不考虑棒束之间相互影响的条件下，等效环管的速度分布可使用内径为r1、外径为r2的同心环管在相应位置处的速度分布近似。这里忽略壁面润湿对速度分布的影响［3］，可认为速度最大处的位置仅与r1、r2相关。

3）在不考虑棒束之间相互影响的条件下，等效环管的温度分布可使用内径为r1、外径为r2、内侧等热流密度、外侧绝热的同心环管在相应位置处的温度分布近似。在同心环管最大速度处的温度梯度小于零，不是绝热条件，因为这个假设中包含了如下考虑：实际的棒束系统一般中心的温度高于边缘温度，使绝热条件被破坏；同时内侧加热、外侧绝热的同心环管的研究较深入，这样也可更好地利用已有成果使模型简化。

根据假设2，无论对于层流还是紊流，其截面最大速度在环管内的位置一般认为不变。故可用层流状态下的速度分布与半径的关系得到速度最大处的半径：

式中，y′为径比，y′＝r2／r1。

y′是隐式的，不能直接求解。可求出一系列某一y′对应的yeq，作图拟合出y′与yeq的关系（图2）。数据拟合结果为：

图2 y′与yeq的关系Fig.2 Relationship between y′and yeq

yeq按式（3）计算。式（4）拟合的R2＝1。

经以上分析和假设，棒束的传热问题转化为一径比为y′、内侧加热、外侧绝热的同心环管的传热问题。但棒束传热单元所等效的环管仅是径比为y′的同心环管在r＝r1和r＝req之间的部分。

牛顿冷却公式为：

由式（6）可知，由于热流密度q是相同的，在计算传热系数h时重要的区别是温差Δt。完整同心环管的温差大于传热单元的温差，同时，还需考虑环管对棒束传热近似所带来的影响（假设1），因而，必须对温差进行修正。

Nu的计算公式为：

式中：Dh为等效水力直径；κ为流体导热系数。

由式（7）可知，Dh应使用棒束传热单元的水力直径。由水力直径计算公式可得到水力直径修正：

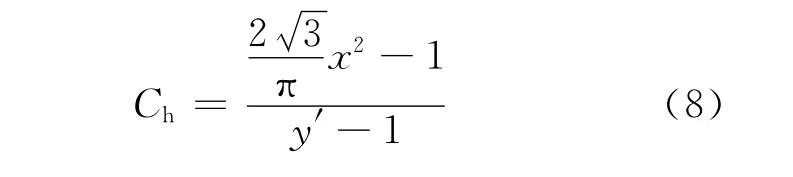
考虑了上述因素后，等边三角形布置的棒束传热关系式为：

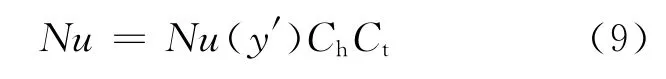
其中：Nu（y′）为径比为y′时对应内侧加热、外侧绝热的同心环管的Nu的计算式；Ch为水力修正项；Ct为温度修正项。

2 温度修正项

如前所述，欲得到棒束传热关系式，须对水力直径和温度进行修正。水力直径修正可直接给出准确的表达式，温度修正则包含了诸多因素，较难给出准确表达式。从前面的分析看，温度修正主要包含两个方面：1）完整同心环管的传热温差大于传热单元所等效的部分环管的传热温差；2）棒束速度场和温度场向环管近似过程方面的修正。

2.1 温度修正的第1项

温度修正第1项与内侧加热、外侧绝热的同心环管的截面温度分布和速度分布有关，按截面平均温度的定义，忽略密度、定压比热容随温度的变化，得到两种情况下的平均温差近似表达式：

式中：tw1为内侧壁温；t（r）、v（r）为半径r处流体温度及速度。

从而，温度修正的第1项为：

在计算式（12）时，同心环管的温度分布可用幂级数表示，利用文献［4］中的数据（流体为液钠、汞，Pe为322、700、2 140、3 110），拟合得到如下关系式：

上式拟合的R2＝0.991 4。

速度场按简单的1／7次幂速度分布律估计：

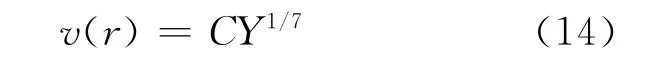
其中：C为常数；Y按式（15）计算［5］。

在不同的y′下计算得到Ct1，结果如图3所示。Ct1由图3可拟合为：

该式拟合的R2＝0.997 4。

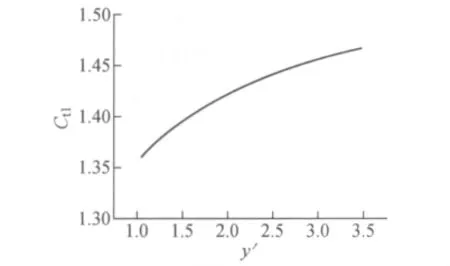
图3 Ct1与y′的关系Fig.3 Relationship between Ct1and y′

需说明的是，以上计算包含了一定估计的因素。虽然速度场按幂律分布这种处理方式在湍流区被广泛应用，但其在层流底层和最大速度处并不符合实际，且在Pe较低时，幂次也不是1／7。另外，环管温度场随着Pe、Pr不同也有所变化，因此，本工作的拟合式与实际有一定偏离，但从拟合的R2来看，引起的偏差不大。

2.2 温度修正的第2项

温度修正的第2项是由环管对棒束布置的近似引起的。棒束的几何条件与简单的环管不同，各棒之间相互影响，其温度场和速度场远比环管复杂，特别是在P／D较小的情况下，各棒之间相对距离小，这种差别更加明显。文献［6］给出不同P／D下局部Nu的变化规律。P／D较小时，Nu随角度的改变很大，而在P／D较高时，Nu在不同角度的值几乎相同。这表明，P／D越小，棒束间的相互影响越明显，几何布置沿周向的非均匀性越突出，速度场和温度场的复杂程度越高；但随着P／D的增大，这种非均匀性迅速减弱，最后逐渐趋于稳定。这体现了棒束间相互影响大小的一般规律。欲得到温度修正的第2项，就必须对这一规律进行较准确的描述。本工作采用的方法是，比较2根圆棒形成的通道与环管最外侧到中心圆棒壁面距离的相对大小，因为这2个值均关系到速度场的发展，进而影响温度场。若该值距1较远，则棒束与环管的温度场与速度场的相似度小，反之，则相似度大。具体表达式为：

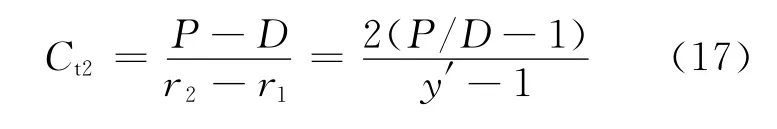
Ct2随P／D的变化规律示于图4。从图4看出，在P／D＜1.3时，随着P／D的增大，Ct2迅速增大；而当P／D＞1.3时，Ct2缓慢上升。

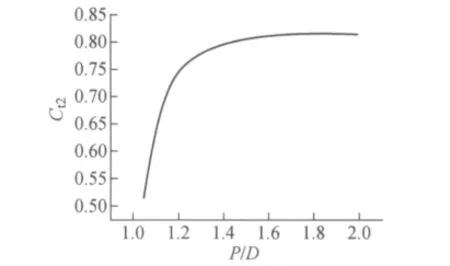
图4 棒束之间的相互影响Fig.4 Interaction among tube bundles

式（17）的计算结果与采用子通道方法计算棒束传热程序中使用的修正因子有效混合长度Lij的计算结果（仅在P／D较小时适用）非常接近［7－8］，图5示出这两种计算结果的比较。

图5 式（17）与有效混合长度的关系Fig.5 Relationship between Eq.（17）and effective mixing length

3 分析讨论

3.1 模型验证

通过将三角形布置的棒束传热问题过渡到同心环管传热问题，经水力直径修正和温度修正，得到三角形布置液态金属棒束传热的计算公式（式（9））。为验证该式的应用价值，与已有的实验数据进行了比较［9－11］。

文献［9］采用由7根22mm圆管构成等边三角形布置的棒束，在不同P／D（1.1、1.2、1.3、1.4、1.5）下测量了传热数据。实验加热段长800mm，温度变化范围为206～236℃，文献中未给出具体工质，但给出每组P／D实验数据所包含的Pr，分别为0.007、0.03、0.024。

文献［10］中实验段采用12mm的31根圆管布置成等边三角形，P／D为1.25、1.6、1.95，实验工质为44%Na－56%K，温度范围为100～425℃，Pr变化范围为0.011～0.024。文献中给出了246组数据，本工作使用了Pe在110～4 300范围内的数据。

文献［11］采用了13根13mm的圆棒构成P／D＝1.75的等边三角形布置，对汞进行了传热实验（Pr＝0.02），实验结果包含了146组实验数据。本工作分析中，使用了Pe在150～4 000的实验数据。

图6示出本工作计算结果与实验数据的比较。温度修正采用不同的关系式计算。图中的温度修正项拟合式按上述实验数据拟合而得：

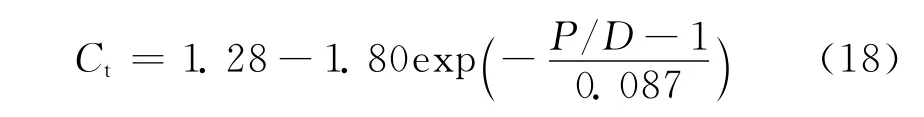
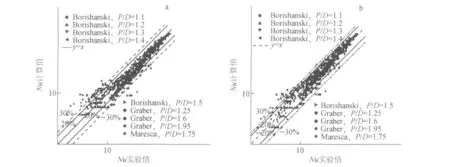
图6 实验结果与引用不同温度修正的计算结果的比较Fig.6 Comparison between experimental data and calculated values with different temperature corrections a——式（16）、（17）；b——式（18）

图6a的温度修正按式（16）、（17）计算。整体看来，几乎所有的实验数据都均匀地分布在y＝x这条直线两侧，Nu的计算结果对实验数据实现了很好的预测。在P／D≥1.2时，与实验数据的相对误差均在30%以内，但在P／D＝1.1时，很明显地高估了实验数据，约有一半数据的相对误差均大于30%。在P／D很小时对实验数据的偏离，应是这个情形下棒间间距过小、从等边六边形向圆形的等效近似导致传热几何的较大变化引起的。

图6b的温度修正项按实验数据拟合得到。整体看来，几乎所有实验数据与计算结果的相对误差均在±30%以内，且无明显高估或低估实验数据的趋势，预测效果良好。在P／D较大时，实验数据与预测结果的相对误差几乎均在±20%以内，随着P／D减小，预测效果降低。

3.2 讨论

经上述比较可见，在实验数据范围内，本工作所建立的模型取得了良好效果。对于P／D≥1.2，与实验数据估计的相对误差基本可在30%以下，在高Pe区的预测精度则更高。这充分说明了本模型的合理性，但使用该模型还需注意以下问题。

1）本模型在P／D＜1.2的情况下，对实验数据的预测偏高。初步估计是在小P／D情况下，从等边六边形向圆形的简化假设会引入较大误差，因为这种情况下，传热单元的面积受边界形状的影响增大，简化会引起传热几何上的巨大变化。若要在较低P／D情况下使用该模型，应引入对这一方面的修正。

2）本模型温度修正的第1项虽有明显的物理意义，但本工作给出的修正公式仅针对Pr很小的液态金属，且Pe在一定范围内适用，若条件有所改变，应相应地改变修正公式。

3）本模型温度修正的第2项虽导出过程的物理意义不十分明确，但从其与有效混合长度在计算结果上的一致性来看，其物理含义和准确计算可参考有效混合长度的相应结论。

4）本模型仅对等边三角形布置的棒束进行讨论，对于正方形布置的棒束传热，应引入一项几何上的修正。

4 结论

棒束传热问题可转化成内侧加热的同心环管的传热问题，本工作研究了这一过程，同时得到棒束传热的新关系式，通过与实验数据的对比讨论，取得较好的预测效果。本工作的结论如下。

1）液态金属三角形布置顺流传热关系式为：

拟合公式为：

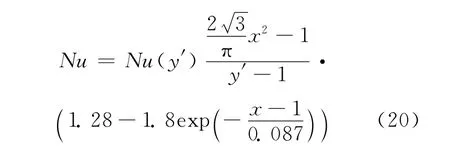
以上两式中：

Nu（y′）表示径比为y′时对应内侧加热、外侧绝热的同心环管的Nu的计算式，可按Dwyer等［12］给出的关系式计算。式（19）可在1.2≤P／D＜2范 围 内 使 用；式 （20）可 在1.1≤P／D＜2范围内使用。根据实验数据和参数拟合范围，以上两式适用于Pr≤0.03的液态金属，其中100＜Pe＜4 300。

2）进行温度修正第2项计算时发现，本工作提出的温度修正第2项关系式（式（17）），与已有的有效混合长度关系式符合较好，可作为有效混合长度的新关系式使用。

［1］DWYER O E，TU P S.Analytical study of heat transfer rates for parallel flow of liquid metals through tube bundles［J］.Chemical Engineering Progress Symposium Series，1960，56（30）：183－193.

［2］FRIEDLAND A J，BONILLA C F.Analytical study of heat transfer rates for parallel flow of liquid metals through tube bundles［J］.AIChE Journal，1961，7（1）：107－112.

［3］HLAVAC P J，NIMMO B G，DWYER O E.Experimental study of effect of wetting on turbulent flow of mercury in annuli［J］.Int J Heat Transfer，1972，15（12）：2 611－2 631.

［4］GÜNTHER G.Numerical simulation of turbulent temperature fluctuations in liquid metals［J］.International Journal of Heat and Mass Transfer，1981，24（3）：475－490.

［5］HENRY B.Fluid flow and heat transfer in an annulus with heated core tube［J］.ImechE，1955，169（1）：1 113－1 124.

［6］CHENG X，TAK N I.CFD analysis of thermalhydraulic behavior of heavy liquid metals in subchannels［J］.Nuclear Engineering and Design，2006，236（18）：1 874－1 885.

［7］JEONG Hae－yong，HA Kwi－seok.Evaluation of the conduction shape factor with a CFD code for a liquid metal heat transfer in heated triangular rod bundles［J］.Nuclear Engineering and Design，2007，237（6）：648－654.

［8］CHENG S K，TODREAS N F.Constitutive correlations for wire－wrapped subchannel analysis under forced and mixed convection conditions，DOE／ET／37240－108TR［R］.USA：Massachusetts Institute of Technology，1984.

［9］BORISHANSKI V M，GOTOVSKI M A，FIRSOVA E V.Heat transfer to liquid metals in long itudinally wetted bundles of rods［J］.Atomnaya Energiya，1969，27（6）：549－552.

［10］GRÄBER V H，RIEGER M.Experimentelle untersuchung des wärmeübergangs an flüssigmetalle（NaK）in parallel durchströmten rohrbündeln bei konstante und exponentieller wärmeflussdichteverteilung［J］.Atomkernenergie （ATKE）Bd，1972，19（1）：23－40.

［11］MARESKA M V，DWYER O E.Heat transfer in a mercury flow along bundles of cylindrical rods［J］.Journal of Heat Transfer，Transactions ASME，1964，64：180－186.

［12］DWYER O E，TU P S.Bilateral heat transfer to liquid metals flowing turbulently through annuli［J］.Nucl Sci Eng，1965，21（1）：90－105.