浓缩回收铀的M级联的近似算法
谢全新,耿冰霜,吴建军
(核工业理化工程研究院,天津 300180)
二元同位素分离级联的设计通常以理想级联[1]为基础,使实际级联的结构尽量逼近理想级联。理想级联是在级的混合管处无丰度混合损耗的级联,即效率最高的级联。在多元即多组分同位素分离级联中,不可能使所有组分在级的混合管处无丰度混合损耗,但可建立一种级联,使其中某两个组分的相对丰度在级的混合管处相等,这样的级联即为丰度比匹配级联(Matched Abundance Ratio Cascade),简称为M级联[2-3]。多元分离的M级联类似于二元分离的理想级联。
某些特殊的分离任务需借助附加供料级联,如核燃料循环中回收铀的再浓缩[4-6]利用了附加供料级联,以天然铀为主供料,回收铀为附加供料。本文将以带附加供料的M级联的数学模型为基础,利用回收铀浓缩的特殊性,提出一种浓缩回收铀M级联的近似算法。
1 带附加供料的M级联的数学模型
带附加供料的M级联(图1)的外参量有主供料流F、附加供料流E、精料流P及贫料流W,相应的组分丰度分别为CiF、CiE、CiP、CiW(i=1,…,m,m为待分离同位素混合物的组分数),级联总级数为N。精料从第N级取料,贫料从第1级取料。此外,主供料从第f级供入,而附加供料从第l级供入。上述参量之间存在以下关系[7-8]:

级联总相对流量可通过下列关系式来计算[7-8]:

式(1)~(5)中的gi是第i组分的精料流与贫料流之比[2-8],可表示为:
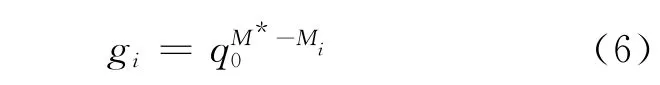
式中:q0为基本全分离系数;Mi为第i组分的摩尔质量;M*为两关键组分(如第n和第k组分)摩尔质量的平均值,即:
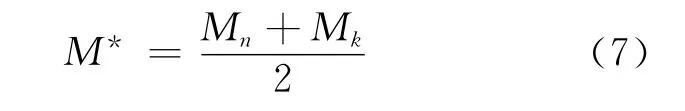
多组分同位素分离级联的计算从功能上可分为两类:一类是验证计算,即对级联结构和运行参量已确定的级联进行计算,来验证理论计算结果与实际运行数据是否相符。对于带附加供料的M级联,如级联总级数N、主供料级f、附加供料级l、主供料丰度CiF、附加供料丰度CiE及gi和E/F已知,由式(1)~(4)可求出相对流量F/P、F/W、精料组分丰度CiP和贫料组分丰度CiW,之后根据式(5)可求出M级联的总相对流量LT/P。另一类是设计计算,即针对一定分离任务,确定级联结构和运行参量,使级联最经济。如给定目标组分的精料丰度CnP和贫料丰度CnW,确定级联结构,即确定总级数N、主供料级f、附加供料级l,使级联总流量最小。这类计算实际是一以目标组分的精料丰度CnP和贫料丰度CnW为约束条件,以级联总相对流量LT/P为目标函数,以总级数N、主供料级f、附加供料级l为优化变量的带约束条件的非线性规划问题。该类计算较第1类计算复杂得多,必须借助专门的工程优化方法来完成。

图1 带附加供料的M级联示意图Fig.1 Scheme of M cascade with additional feed flow
2 用于回收铀浓缩的M级联的近似算法
回收铀的浓缩必须同时考虑232U的净化和236U 的 补 偿 问 题 。 理 论 研 究[4-5]表 明 ,浓 缩回收铀的最有效的级联形式是带附加供料的级联。天然铀作主供料,回收铀作附加供料。天然铀和回收铀的组成及其组分丰度列于表1。表1中回收铀的组分丰度为俄罗斯轻水堆VVER-440堆后料经10年储存期后的典型丰度。

表1 天然铀和回收铀的组成及其组分丰度Table 1 Composition and component abundances in natural and recycled uranium
本文所讨论的近似算法主要是针对第2类级联计算,即已知目标组分的精料丰度和贫料丰度,确定级联结构。毫无疑问,回收铀浓缩时的目标组分为235U,假设目标组分的精料丰度C3P=3.5%,贫料丰度C3W=0.2%。欲确定级联结构,即确定级联总级数N、主供料级f、附加供料级l,必须利用有效的工程优化方法。但回收铀的浓缩有其自身的特殊性。首先,作为主供料的天然铀,只含有两种组分235U和238U,即表1中的C1F=C2F=C4F=0。其次,作为附 加 供 料 的 回 收 铀,232U、234U 和236U 相 对235U和238U属微量组分。这两个特殊性允许在回收铀级联计算中做某些合理的近似处理,从而大为简化计算。下面将详细讨论用于回收铀浓缩的M级联的近似算法。
在带附加供料的M级联中,第i组分在4股外部流中的组分守恒方程可表示为:
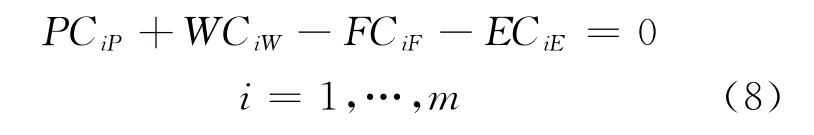
同时满足下面的H平衡方程:
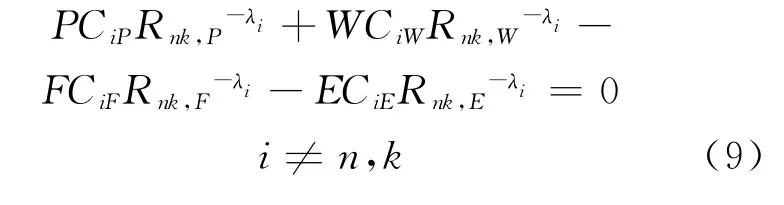
其中:Rnk,F、Rnk,E、Rnk,P、Rnk,W分别表示级 联 主供料、附加供料、精料与贫料流中n、k两关键组分的相对丰度,即:
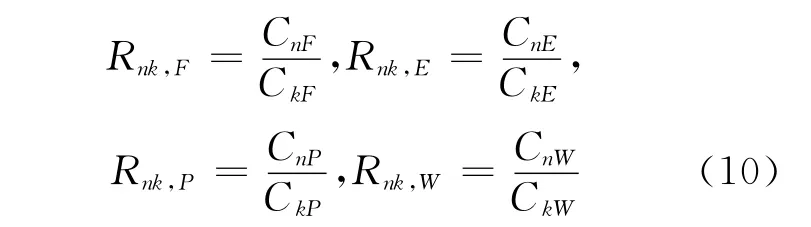
式(9)中的λi是与组分有关的量,可表示为:
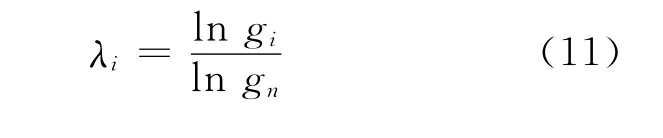
H平衡方程由Garza[2]首先提出,起初主要针对分离系数小的不带附加供料的普通扩散级联。之所以称之为H平衡方程,是因为方程中定义了一齐次函数(H函数)。式(9)中第i组分的 H函数可表示为Hi=CiRnk-λi,这样,式(9)可改写为:
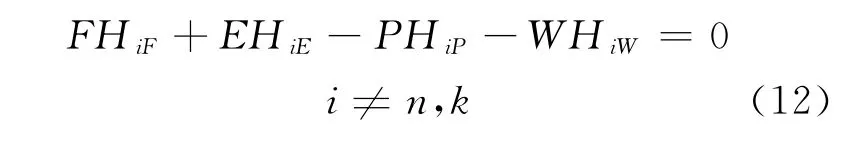
由于235U 和238U 的丰度在天然铀和回收铀中均占有绝对优势,所以把他们作为关键组分来进行计算是合理的,即在计算gi时,式(7)中的n=3、k=5。这样,根据式(6)~(7)可计算出各组分的gi,即:

借助式(13)可把式(9)表达成如下形式:
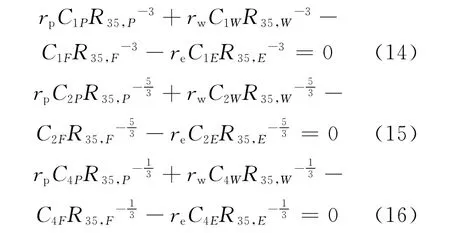
其中:rp=P/F;rw=W/F;re=E/F。
组分质量守恒方程保留原有形式并可分列如下:
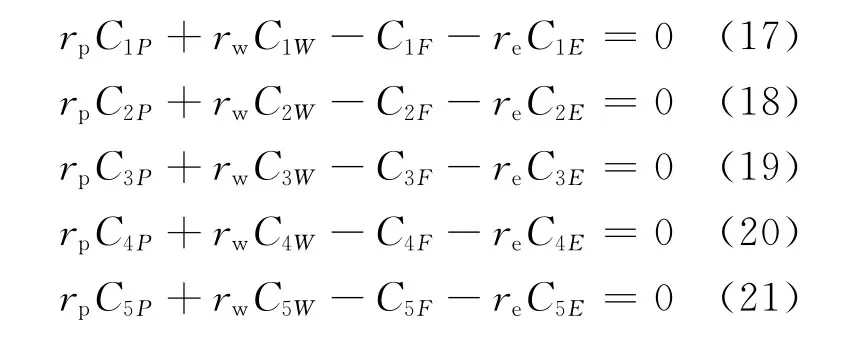
利用式(19)和下列级联流量守恒方程:
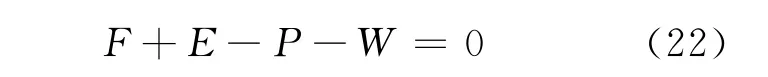
可求得rw和rp,即:

式(23)~(24)中的re为自由变量,一般人为给定。
在回收铀中,235U与238U两组分的丰度在同位素混合物中占绝对优势,因此,可作如下近似:
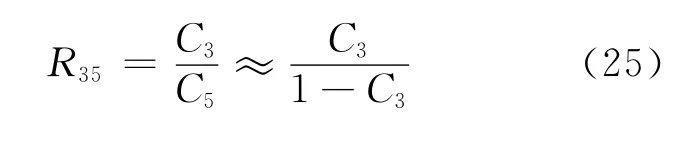
这样,通过求解方程组(14)和(17)并考虑到作为主供料的天然铀中不含232U,即C1F=0,可得到232U 的精料丰度C1P和贫料丰度C1W:
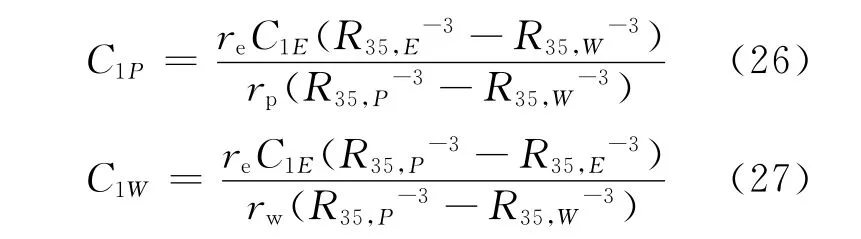
同理,可求得234U、236U 的精料丰度和贫料丰度:
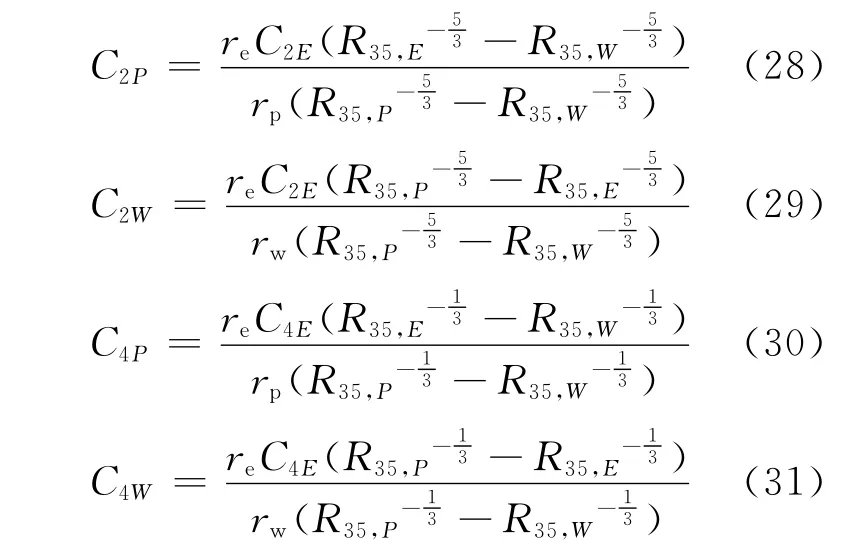
目标组分235U在级联主供料、附加供料、精料和贫料流中的丰度C3F、C3E、C3P、C3W是已知的,附加供料与主供料流量之比re一般预先给定,因此,根据式(23)~(24)可求出rw、rp。由式(10)并考虑近似关系式(式(25))可求得两关键组分在4股外部流中的相对丰度Rnk,F、Rnk,E、Rnk,P、Rnk,W。然后根据式(26)~(31)可求得232U、234U 和236U 3个组分的精料丰度和贫料丰度。238U的精料丰度和贫料丰度可由丰度归一化条件=1直接求出。至此,回收铀中全部5个组分的精料丰度和贫料丰度均已确定。
在级联设计计算中,还须确定级联总级数N、主供料级f、附加供料级l,这3个参量可由下式直接求出:

而级联中总的相对流量可由下式确定:

式(32)~(35)在文献[7-8]中有详细推导。
无论是由式(26)~(31)计算组分丰度,还是由式(32)~(35)确定级联结构和级联总流量,均为简单的解析求解,无须复杂的编程计算,使用普通的计算器即可完成计算。这是近似算法的最大优点。
3 近似算法与优化算法的比较
为验证近似算法的合理性,将近似算法与优化算法的结果进行比较。根据式(1)~(5)进行优化计算时,先利用罚函数法将约束优化问题转化为无约束优化问题,然后用单纯形法求解。计算中天然铀和回收铀取表1所列的供料丰度,回收铀和天然铀的供料量之比re=1。两种方法得到的计算结果列于表2。

表2 优化算法与近似算法的计算结果Table 2 Calculation results obtained by using optimization method and approximate method
由表2可看出,近似算法与优化算法的计算结果非常接近。通过改变re和回收铀的组分丰度,进行了一系列计算,也得到相同的结论,即两种算法的结果非常接近,最大相对偏差小于0.1%。因此,对于浓缩回收铀的 M级联,采用本文所提供的近似算法是合理的,且近似算法更方便和快捷。
4 结论
利用浓缩回收铀的特殊性,提供了一浓缩回收铀的带附加供料的M级联的近似算法。得到了求解精料组分丰度、贫料组分丰度、级联总级数、主供料级和附加供料级以及级联总流量的近似计算式。所有计算都无须复杂的编程,使用最普通的计算器即可算出结果。数值计算表明,近似算法与工程优化算法得到的结果非常接近,最大相对偏差不超过0.1%,但近似算法相对于工程优化算法具有简单、方便、快捷的优点。
[1]COHEN K.The theory of isotope separation as applied to the large scale production of235U[M].USA:Mc,Graw Hill Book Co.Inc.,1951.
[2]GARZA A D L.A generalization of the matched abundance-ratio cascade for multicomponent isotope separation [J].Chemical Engineering Science,1963,18:73-82.
[3]von HALLE E,TENNESSEE O R.Multicomponent isotope separation in matched abundance ratio cascades with losses from each stage[C]∥Proeeding of 1st Workshop on Separation Phenomena in Liquids and Gases.Darmstadt,Germany:[s.n.],1987:325-356.
[4]SULABERIDZE G A,BORISEVICH V D,XIE Q X.On some separation problems on regenerated uranium application in the fuel cycle [C]∥Proceedings ofⅨ All-Russia(International)Scientific Conference: Physical and Chemical Processes on Selection of Atoms and Molecules.Zvenigorod,Russia:[s.n.],2004:70-77.
[5]SULABERIDZE G A,BORISEVICH V D,XIE Q X.Study of regularities of stationary mass transfer in separating cascade for enrichment of regenerated uranium [J].Engineering Physics,2005(3):15-19.
[6]谢全新,李大勇,吴建军.回收铀分离级联计算[J].核技术,2009,32(1):61-65.XIE Quanxin,LI Dayong,WU Jianjun.Cascade calculations for separation of recycled uranium[J].Nuclear Techniques,2009,32(1):61-65(in Chinese).
[7]XIE Quanxin.Stationary molecular selective transfer in ordinary and multiflow cascades with large enrichment factors and losses at stages for the separation of multicomponent isotopic mixture[D].Moscow:Moscow Engineering Physics Institute,2007.
[8]SULABERIDZE G A,BORISEVICH V D,XIE Q X.Quasi-ideal cascades with an additional flow for separation of multicomponent isotope mixtures[J].Theoretical Foundations of Chemical Engineering,2006,40(1):7-16.

