矩形窄通道内DRYOUT模型研究

周 磊，闫 晓，黄善仿，黄彦平，肖泽军

（1.中核集团 核反应堆热工水力技术重点实验室，四川 成都 610041；2.清华大学 工程物理系，北京 100084）

临界热流密度（CHF）发生时，冷却剂对流换热系数减小、燃料元件壁温升高，严重的可使燃料元件烧毁从而引起放射性泄漏。因此，准确预测CHF对于反应堆设计和安全分析具有重要的意义。通常认为在环状流区，CHF是由液膜的干涸引起，据此建立的CHF预测模型常称为液膜干涸（DRYOUT）模型。由于环状流型所对应的含汽率范围广泛（约0.1～1.0），DRYOUT不仅对于沸水堆，而且对于压水堆的安全分析及瞬态过程均具有很重要的意义。近年来，DRYOUT模型倍受重视［1－2］。

板型燃料元件结构紧凑，有利于提高堆芯功率密度、减小堆芯体积，在一些研究堆、新型核动力堆和国外生产堆中已得到应用。其冷却剂流道是窄缝隙的矩形通道。矩形窄通道在一些电子设备的冷却中也有重要应用，因此相关热工水力性质已成为研究热点［3］。

文献中已有的DRYOUT模型主要是面向圆管常规通道开发的，对于矩形窄通道是否可用、性质如何，缺乏足够的实验数据验证。本文通过优化DRYOUT模型中重要本构关系式的组合、适当选取模型中的沉积率和夹带率等公式，以得到适用于矩形窄通道的DRYOUT模型。

1 流动结构和控制方程

图1为矩形窄通道中DRYOUT模型的示意图。由于热量的加入，沿流动方向含汽率逐步升高，当达到某一转变值xt时流型进入环状流；在环状流区，蒸汽在通道中间流动形成汽芯，液体则一部分沿壁面形成液膜，一部分以夹带液滴的形式存在于汽芯中。由于蒸发、液滴沉积及夹带等过程的共同作用，液膜流量沿流向逐渐变小，液膜厚度逐渐变薄。对于通道均匀加热的情况，若在通道出口处液膜厚度足够小，此时的热流密度即为临界热流密度。

图1 环状流区干涸模型示意图Fig.1 Sketch of DRYOUT model in annular flow regime

取通道上长度为Δz的一段，液膜的连续性方程为：

其中：Wlf为液膜质量流量，kg／s；me、md、mv分别为夹带率、沉积率和蒸发率，kg／（m2·s）；ξi和ξh分别为汽芯和液膜的交界面周长和热周，m；z为流动方向的坐标，m。

对于圆管通道，热周和界面周长相等，并可取为通道周长。而矩形通道热周取决于具体加热情况，而界面长度可近似取为通道周长。令Δz→0，即得Wlf满足如下控制方程：

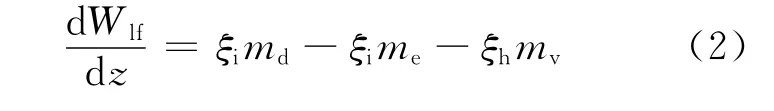
在DRYOUT模型中通常假设液膜的温度近似为对应压力下的饱和温度，加入的热量全部用于液体蒸发，因此有：

其中：qw为壁面热流密度，W／m2；hfg为汽化潜热，J／kg。

因此，只要给定环状流起始点和沉积率、夹带率公式及相应的本构方程，通过式（2）即可求得任意位置处的液膜质量流速，进而通过迭代过程可求得在出口发生干涸时对应的CHF。

2 本构方程

2.1 环状流起始点条件

对于环状流起始点，文献中发表了大量的判定关系式。敏感性计算表明，在DRYOUT模型中，当加热板长度较小或临界含汽率较小时，环状流起始点对CHF有显著影响，因而环状流起始点判据须慎重选取。本文选取著名的Mishima ＆ Hibiki关系式［4］作为判据：

其中：Jv为汽相表观速度；σ为表面张力，N／m；ρv为汽相密度，kg／m3；Δρ为液相和汽相密度差，kg／m3；g为重力加速度，即9.81m／s2。

上式是专门针对矩形窄通道建立的。

无量纲粘度数Nμf定义如下：

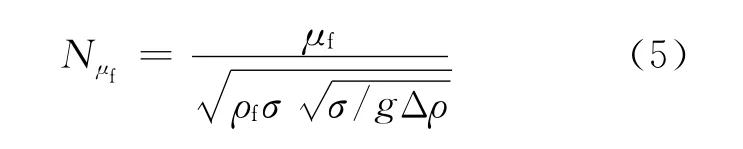
其中：μf为液相粘度，Pa·s；ρf为液相密度，kg／m3。

王俊峰［5］通过流型可视化实验证实矩形窄缝通道中环状流存在且可用式（4）进行较好预测。

2.2 沉积率和夹带率关系式

敏感性计算表明，沉积率和夹带率对液膜质量流量或液膜厚度有着全程性的影响，因而对计算的CHF有显著影响。但文献中公开发表的沉积率、夹带率关系式数量众多。本文仅选取5组应用广泛的关系式进行简要介绍和比较，这5组关系式均是在大量的液滴沉积实验数据的基础上拟合得到的，有的还被用于已有的反应堆热工水力分析程序中，具有较好的通道适用性。

1）Wurtz－Sugawara关系式（case 1）

由Sugawara对Wurtz关系式进行改进得到，以便更好地体现压力的影响，改进后的公式在COBAR－TF子通道分析程序中得到应用［6］：

其中：ug为汽相平均速度，m／s；τi为汽液界面摩擦应力，N／m2。

其中：uf为液膜平均速度，m／s。系数k为：

其中：Reg为汽相雷诺数。

ks为等效沙粒粗糙度（无量纲），由实验数据拟合得到：

式中：δ为液膜厚度，m。

液滴沉积率和液滴浓度成正比，即：

其中：C为液滴浓度，kg／m3；kd为沉积率系数，m／s，由下式计算：

其中：Sc为无量纲斯密特数。

汽芯中液滴浓度C定义如下：

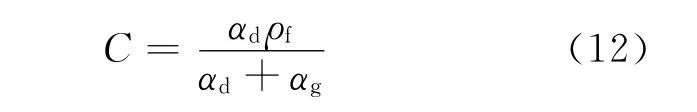
式中：αd、αg分别为液滴和汽相的体积份额。

2）Govan关系式（case 2）

Govan等［7］直接对沉积和夹带实验数据进

行拟合，得到：

其中：min表示取小值函数；D为通道等效直径，m。

夹带率为：

其中：Gg、Glf分别为汽相和液膜质量流速，kg／（m2·s）。

临界液膜质量流速Glfc由下式给出：

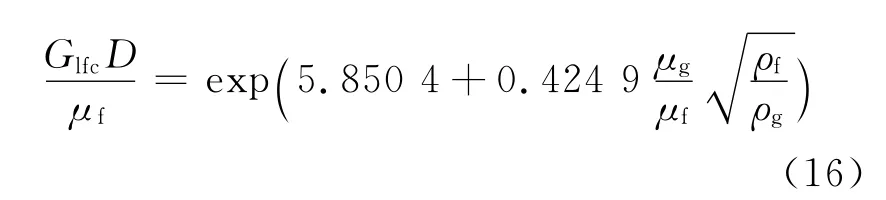
3）Okawa ＆ Tsuyoshi关系式（case 3）

他们假设夹带率和界面剪切应力成正比，而和表面张力成反比，首先定义无量纲数π［8］：e

式中：fi为剪切应力系数。

则夹带率可表示为：

并且只有当液膜雷诺数Relf足够大时，才发生液滴的夹带，即：

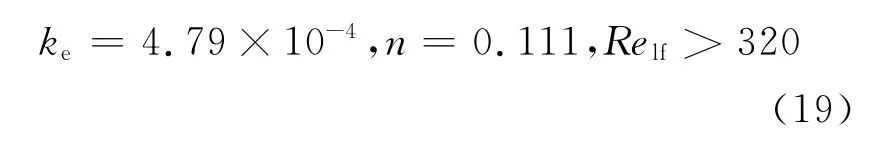
对于沉积率，Okawa和Tsuyoshi等的研究结论是高压下Govan公式较好，而低压下Sugawara公式更好，因此他们的沉积率关系式是二者的线性组合（对于Govan公式有少量修改以消除原公式的不连续性）：

权重w的大小取决于压力以及含汽率的情况。

4）Kataoka ＆Ishii关系式（case 4）

Ishii ＆ Kataoka给出的沉积率关系式［9］如下：

其中：E为汽芯中夹带液滴在全部液相质量中的比重。

Ishii ＆Kataoka给出的夹带率公式考虑了入口效应等，因此结构上较为复杂，即：

E∞为平衡夹带份额，按下式计算：

而夹带Webber数定义为：

当液膜雷诺数小于某临界值时，夹带不会发生，临界液膜雷诺数为：

5）Okawa ＆ Kataoka关系式（case 5）

Okawa和 Kataoka［10］对沉积实验数据分析后认为，实验数据难以使用统一的函数形式表达。当液滴浓度较高时，沉积率系数可视为液滴浓度的函数，即：

式中：C＊为无量纲液滴浓度；k＊d为无量纲沉积率系数。

当液滴浓度很低时，沉积系数是摩擦速度的函数：

uτ为摩擦速度，m／s，定义为：

其中：τw为壁面摩擦应力，N／m2。夹带率公式的拟合思路和Okawa ＆Tsuyoshi等相同，只是函数形式略有改变：

无量纲量πe1为：

临界汽相表观速度Jgc为：

若汽相表观速度低于临界值，则夹带率为0。

2.3 沸腾夹带率

上述沉积率和夹带率公式均是根据绝热等温实验数据拟合得到的，并未考虑汽化过程的影响。实际上对于有加热的情况，汽泡不断产生并进入汽芯，也会形成液滴夹带，因此对于有加热的情况，总的夹带率应为：

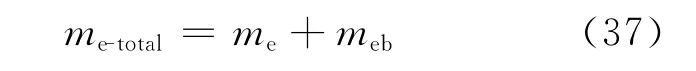
meb为沸腾夹带率，kg／（m2·s）。本文采用 Ueda公式［11］计算：

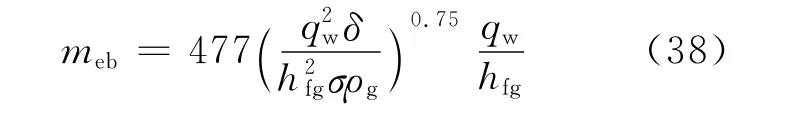
其中，液膜厚度可根据液膜质量流量求得。

2.4 统计参量和评价实验数据库

由于缺乏矩形窄通道沉积率和夹带率实验数据，不能对上述关系式进行直接评价。但可将这些关系式引入DRYOUT模型中，通过和CHF实验数据的对比，得到最优的DRYOUT模型。为此，收集准备了矩形窄通道CHF实验数据库，参数范围列于表1。表中DRYOUT数据是根据Mishima ＆Hibiki关系式［4］选出的。

按照习惯，定义如下统计参数。模型计算偏差CHFR，表示CHF模型计算值与实验值之比：

模型平均偏差，即CHFR的平均值为：

标准偏差仅体现CHFR的分散程度，若CHFR分布散度很小但总体倾斜很大，结果仍不好，因此引入CHFR的分布带宽BW：

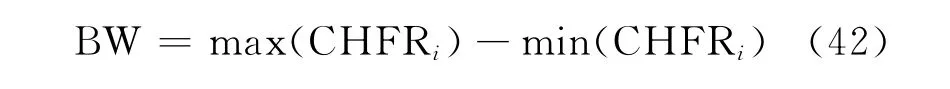
其中，N表示样本总数。

标准偏差为：

表1 矩形窄通道CHF实验数据库Table 1 Experimental database for CHF in narrow rectangular channel

3 模型开发结果

3.1 模型优化过程

图2、3示出了由5组沉积率和夹带率关系式计算得到的CHFR的分布情况，本文仅给出CHFR随质量流速和含汽率的分布。表2列出了采用不同沉积率和夹带率关系式计算结果的统计特征。

从图2、3和表2可看出，case 1、4的计算结果总体上小于实验值，模型平均偏差仅为0.863 和 0.895，CHFR 的 分 散 度 也 很 大。case 2的结果绝大部分分布在±20%之内，标准偏差也较小，但从CHFR－xC的分布图上看出，当含汽率大于0.25时，模型计算结果偏大。case 5的结果分布趋势和case 2相似，但分散度更大，且有更多点超出了20%偏差线。只有case 3，全部结果的精度在±20%以内，且CHFR的分布带宽BW小于0.3，标准偏差为0.043，这 是 因 为 其 沉 积 率 公 式 是 Wurtz－Sugawara关系式和Govan关系式的线性组合，因此基本消除了case 2中CHF在高含汽率时偏大的现象，结果在5组关系式中最好。因此，Okawa ＆ Tsuyoshi关系式被用于本文的DRYOUT模型中。表3列出了本文DRYOUT模型最终采用的主要关系式。

3.2 与已有DRYOUT模型的比较

对于本文收集的实验数据，同时采用Celata模型和Kataoka模型进行了计算。计算结果的对比见表4和图4。可看出，Celata模型计算结果全部大于实验值，总体偏大约30%。Kataoka模型虽引入了临界液膜的概念，但计算结果总体上仍偏大，且含汽率较低时计算误差更大，这是因为该模型采用了不同的环状流起始点判据，含汽率低于0.2时基本超出了模型的推荐使用范围。而本文模型对于全部实验数据计算精度达到20%，且标准偏差最小，性能明显优于已有模型。

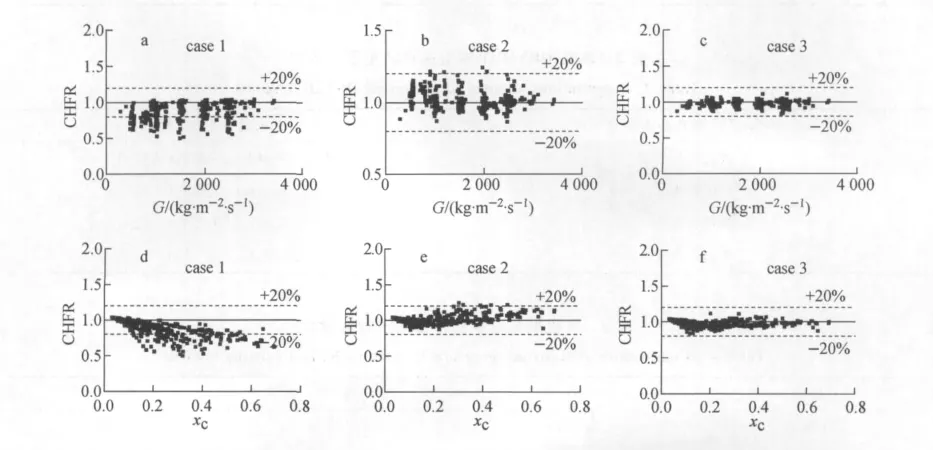
图2 Wurtz－Sugawara（a、d）、Govan（b、e）和 Okawa ＆ Tsuyoshi（c、f）关系式计算结果Fig.2 Caculation results of Wurtz－Sugawara（a，d），Govan（b，e）and Okawa ＆ Tsuyoshi（c，f）correlations

图3 Kataoka ＆Ishii（a、c）和 Okawa ＆ Kataoka（b、d）关系式计算结果Fig.3 Caculation results of Kataoka ＆Ishii（a，c）and Okawa ＆ Kataoka（b，d）correlations

表2 不同关系式得到的DRYOUT模型统计量Table 2 Statistics of DRYOUT models by different correlations

表3 本文DRYOUT模型采用的主要关系式Table 3 Correlations adopted in optimized DRYOUT model

表4 本模型和已有模型结果统计量对比Table 4 Comparison of statistics of results by this model and existing models

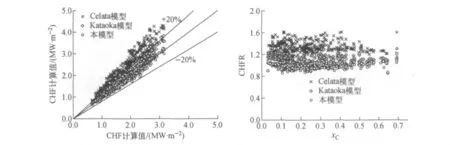
图4 各模型计算值对比Fig.4 Comparison of calculated results by different models

4 结论

矩形窄通道以其特有的热工性能而获得越来越多的关注。本文对DRYOUT型临界热流密度模型进行了研究，主要结论如下。

1）已有的DRYOUT模型主要是面向圆管常规通道开发的，能否适用于矩形窄通道缺乏足够的实验支持；对于本文的实验数据，已有模型计算结果总体偏高，从安全的角度考虑，已有DRYOUT模型不宜直接用于矩形窄通道CHF的预测计算。

2）通过匹配DRYOUT模型中重要中间量的计算和合理选取沉积率、夹带率关系式，得到了对于矩形窄通道适用的优化模型。模型计算结果明显优于已有模型，对本文全部实验数据的计算精度在20%以内，且主要系统参数对CHFR的分布无系统性影响，已用于相关的分析程序中。

［1］CELATA G P，MISHIMA K，ZUMMO G.Critical heat flux prediction for saturated flow boiling of water in vertical tubes［J］.Int J Heat Mass Transfer，2001，44（22）：4 323－4 331.

［2］OKAWA T，KOTANI A，KATAOKA I，et al.Prediction of the critical heat flux in annular regime in various vertical channels［J］.Nucl Eng Des，2004，229（2）：223－236.

［3］HUANG J，HUANG Y P，WANG Q W，et al.Numerical study on effect of gap width of narrow rectangular channel on critical heat flux enhancement［J］.Nucl Eng Des，2009，239（2）：320－326.

［4］HIBIKI T，MISHIMA K.Flow regime transition criteria for upward two－phase flow in vertical narrow rectangular channels［J］.Nucl Eng Des，2001，203（2－3）：117－131.

［5］王俊峰.矩形窄缝通道内水流动沸腾流型及其演变机理研究［D］.成都：中国核动力研究设计院，2010.

［6］SUGAWARA S.Droplet deposition and entrainment modeling based on the three－fluid model［J］.Nucl Eng Des，1990，22（1－3）：67－84.

［7］GOVAN A H，HEWITT G F.An improved CHF modeling code［C］∥Proceedings of the sedond UK national heat transfer conference.London：Oxford University Press，1981：33－48.

［8］OKAWA T，KITAHARA T，KENJI Y，et al.New entrainment rate correlation in annular twophase flow applicable to wide range of flow condition［J］.Int J Heat Mass Transfer，2002，45（1）：87－98.

［9］KATAOKA I，ISHII M，NAKAYAMA A.Entrainment and deposition rates of droplets in annular two－phase flow［J］.Int J Heat Mass Transfer，2000，43（9）：1 573－1 589.

［10］OKAWA T，KATAOKA I.Correlations for the mass transfer rate of droplets in vertical upward annular flow［J］.Int J Heat Mass Transfer，2005，48（23－24）：4 766－4 778.