线性源近似的中子输运方程特征线解法
汤春桃
(上海核工程研究设计院,上海 200233)
中子输运方程的特征线解法是从中子输运方程的一阶微分形式出发,沿特征线进行积分求解的方法,理论上该方法适用于任意复杂几何输运问题的求解。同时,该方法在求解输运方程的过程中无需保存中子角通量和大规模耦合系数矩阵,所以十分节省计算机内存。特征线法早在20世纪50年代即被提出,但直至20世纪70年代才被运用于简单几何的反应堆物理计算中。最近十多年由于计算机硬件水平飞速发展以及工程计算中对复杂几何处理能力的需求,该方法被国际上众多机构广泛研究。近期开发或维护的组件计算程序均采用了这种算法,如 CASMO-4E[1]、HELIOS-2[2]、WIMS[3]、DRAGON[4]等。
但现有的大部分特征线法输运程序均是基于平源近似的步特征线法(SC)模型开发的,平源近似是特征线法理论模型中除角度变量直接离散外又一基本假定。为取得足够的计算精度,该方法须采用足够致密的特征线布置,同时平源近似的区域划分也须足够小。增加平源近似区的数目,一方面会给特征线的布置带来更高的要求,另一方面会增加几何以及相关物理量的存储空间,还会极大地增加相应的跟踪计算时间。
本工作在平源近似的步特征线法理论模型的基础上,提出基于线性源近似的特征线法(LS)改进跟踪计算模型。线性源近似是平源近似的拓展,通过在输运方程右端中子源项部分引入线性项表达式实现。与平源近似的步特征线法相比,它可在采用较大网格剖分的前提下,获得很高的计算精度。其中,中子源项表达式中线性斜率的计算是模型的核心,本文研究该线性斜率的解析表达式,完善坐标投影法的理论模型。此外,在探讨这种改进的数值计算模型的过程中,提出相关负中子源分布的修正方法,使数值收敛过程稳定。
1 理论模型
与SN方法相同,特征线法也是由经角度变量直接离散后的中子输运方程出发的。中子沿某一方向飞行满足稳态多群中子输运方程:

式中:θn为中子飞行方向Ωmn(m为方位角、n为极角)的极角;s为中子运行轨迹在x-y平面的投影;ψg(s)为中子角通量;Qg(s)为该处的中子源项;Σg(s)为宏观总截面;下标g为能群。
在不考虑散射各向异性的情况下,式(1)右端源项可表示为:

式中:χg为裂变份额;keff为有效增殖因数;ν为每次裂变中子数;Σf,g′为裂变截面;Σs,g′→g为散射截面。
从式(2)可看出,Qg(s)应具备与ψ(s)类似的形状分布。实际上,在通常的步特征线法计算模型中,在同一网格i内均未考虑Qg(s)的空间分布,而是将其看作一常数。这是特征线法理论模型中,除角度变量直接离散外又一基本假定。欲在这种平源近似的假定下获得较高的计算精度,特征线法的空间网格离散(即平源近似区)的尺寸须划分得足够小。增加平源近似区的数目、减小平源近似区的尺寸,一方面会增加几何及相关物理量的存储,另一方面也会增加相应的处理时间。同时,还会给特征线的布置提出更高要求。
图1a示出实际压水堆燃料栅元常用的三区模型,欲获得准确的计算结果,在平源近似的特征线法程序中需建立如图1b所示的空间网格划分。基于线性源近似的特征线法会缓解这一问题,它可在采用较大空间网格划分的情况下,依然获得良好的数值计算精度。

图1 燃料栅元三区模型(a)与平源近似区网格划分(b)Fig.1 Fuel cell model with three region(a)and mesh division for flat source approximation(b)
1.1 步特征线法
根据式(1),从中子输运方程的一阶微分形式出发,在假设网格i内宏观截面和中子源强为常数的前提下,穿过该网格的第k条特征线的出射中子角通量可表示为:


由此,网格i内的平均标量中子通量可通过式(3)在所有网格i内的特征线及所有离散方向上积分获得:

式中:ωm和ωn分别为对应离散方向Ωmn的辐角和极角权重;δAm为特征线间的投影间隔;Ai为网格i的面积。
为保证实际区域i的面积守恒,几何扫描产生特征线时,投影长度sm,i,k需经式(5)修正:

1.2 线性源近似特征线法
在笛卡尔坐标(x-y)系统内,本工作探讨的线性源特征线法模型的右端源分布采用如下表达形式:

为源分布的线性斜率,可表示为:
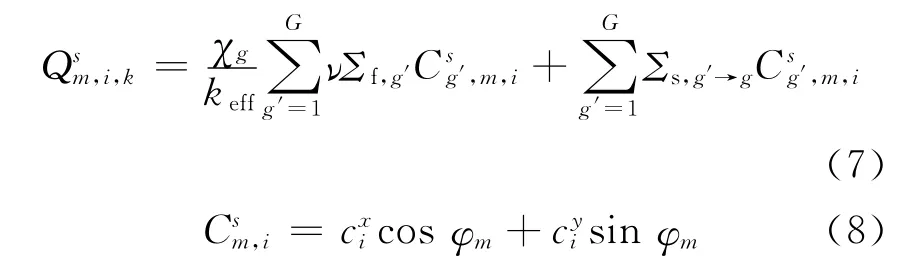
图2示出坐标投影法示意图。
在假设入射中子角通量、网格i的平均源强Qi和线性斜率已知的情况下,将式(1)沿特征线k积分,即可求得出射角中子通量的表达式:

图2 坐标投影法示意图Fig.2 Sketch map for projection method

其中:τ=Σism,i,k/sinθn,为三维空间的光学距离;Ei函数可按下式定义:

根据式(9)求得出射角中子通量后,更新网格平均标量中子通量,进而更新散射源、裂变源等过程与平源近似的步特征线模型相同。需注意,每完成1次外迭代均需根据出射角中子通量更新线性斜率的贡献项、:

式中:Km为经过区域i、方向为m的特征线总数目;Nθ、Nφ分别为方向离散辐角和极角的总数目。
在线性源近似模型中,中子源强分布函数非负是数值计算过程中对物理量的基本要求。式(6)右端项非负的充要条件是:

其中,(sm,i,k)max是特征线段sm,i,k在 网格i内的最大值。
在投影法求线性斜率的过程中,式(12)并不能自动满足,这意味着若不做相应的修正,很有可能出现负中子源强,这是不允许发生的。
在迭代求解过程中,一旦式(12)得不到满足,程序将会在保留原斜率符号的前提下自动调整它的数值,即:
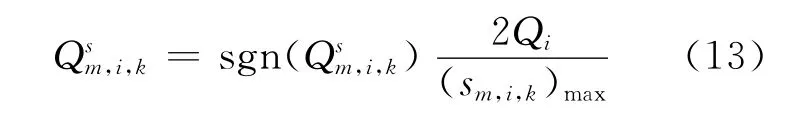
在实际计算过程中,不满足式(12)的情况绝大部分只发生在迭代初期。经基准题的数值检验,式(13)的修正方式可使整个收敛过程更稳定。另外,它既不影响网格内的中子平衡,又在物理量可允许的范围内最大限度地考虑到了中子源强的线性分布,是一种非常有效的修正方法。
2 数值检验
根据上述理论模型,在自行研制的特征线法程序PEACH[5-6]中加入了线性源近似的计算模型,该模型的引入并不影响程序中原有的几何处理方法以及各种加速方法的实施。为了检验线性源近似模型的精度与速度,采用由OECD/NEA发布的广泛用于检验输运程序求解非均匀堆芯能力的C5G7-MOX 2D基准问题[7]和自定义沸水堆小堆芯问题。
2.1 C5G7-MOX 2D基准问题
该基准题堆芯由UO2燃料组件和MOX燃料组件混合装载,共计16盒燃料组件,呈1/8对称。由于它具有强泄漏、组件间能谱差异大、非均匀性强等特点,目前被美、日、韩等国家的研究机构广泛用于新一代堆芯物理分析。关于该基准题的具体几何结构和各种材料的宏观截面等参数参考文献[7]。
程序PEACH在计算C5G7-MOX 2D基准问题时,将特征线法的标准控制参数设定为:1/8卦限内辐角数目为10、极角数目为3,平均相邻特征线间的间隔为0.02cm,每燃料栅元内的网格数为48(图3),靠近燃料棒的4列反射层栅元采用6×6等分、再外面的反射层采用4×4等分。该标准参数下的数值结果由PEACH的平源近似步特征线法模型给出。
表1列出C5G7-MOX 2D问题特征线法平源近似和线性源近似结果比较。从表1可见,PEACH已达到文献[7]公布的国际同类软件的计算精度。

图3 C5G7-MOX 2D燃料栅元的2种网格划分Fig.3 Two types of fuel cell division employed for C5G7-MOX 2Dproblem
为展示本工作提出的线性源特征线法的优越性,将控制参数放松为:1/8卦限内辐角数目为8、极角数目为3,平均相邻特征线间的间隔为0.04cm,每燃料栅元内的网格数为8(图3),反射层栅元均采用4×4等分。由表1可知,一旦平源近似网格划分较大,平源近似特征线法模型的精度将受到影响,keff的偏差为29pcm、棒功率的最大相对偏差可达4.18%。图4分别示出这两种计算模块得出的精细棒功率相对偏差分布。由图4可见,平源近似特征线法的棒功率分布明显存在倾斜。这一现象是较易理解的,靠近反射层的燃料栅元内注量梯度很大,较大网格的平源近似模型很难体现源的梯度。
但在相同控制参数的情况下,线性源近似特征线法模块可给出与标准参数下精度相当的计算结果。另外,从计算机的耗时和存储量两方面来看,线性源近似特征线法模型均是标准参数下平源近似特征线法模块的1/2,可见,线性源近似特征线法具备较明显的优势。
2.2 自定义沸水堆小堆芯问题
该问题的1/4堆芯由9盒燃料组件组成,堆芯外围是宽度为15.24cm的水反射层。堆芯布置如图5所示,燃料组件的外形尺寸为15.24cm×15.24cm,分成两种类型,一种是新料(组件编号为1、2、3),另一种是燃耗深度为20GW·d/tU的旧料(组件编号为4、5、6)。
燃料组件内部共含有6种富集度的UO2燃料和2种类型的含GD燃料棒。燃料栅元为三区的几何结构,分别是燃料、包壳、冷却剂。组件中心位置为约2×2栅元尺寸的水洞,每1/4组件由5×5的燃料栅元规则排列组成。燃料组件外围由盒壁固定,盒壁与燃料间有很窄的间隙,盒壁外面分别是宽水隙和窄水隙,其中,宽水隙是为给控制棒提供足够的插入空间。
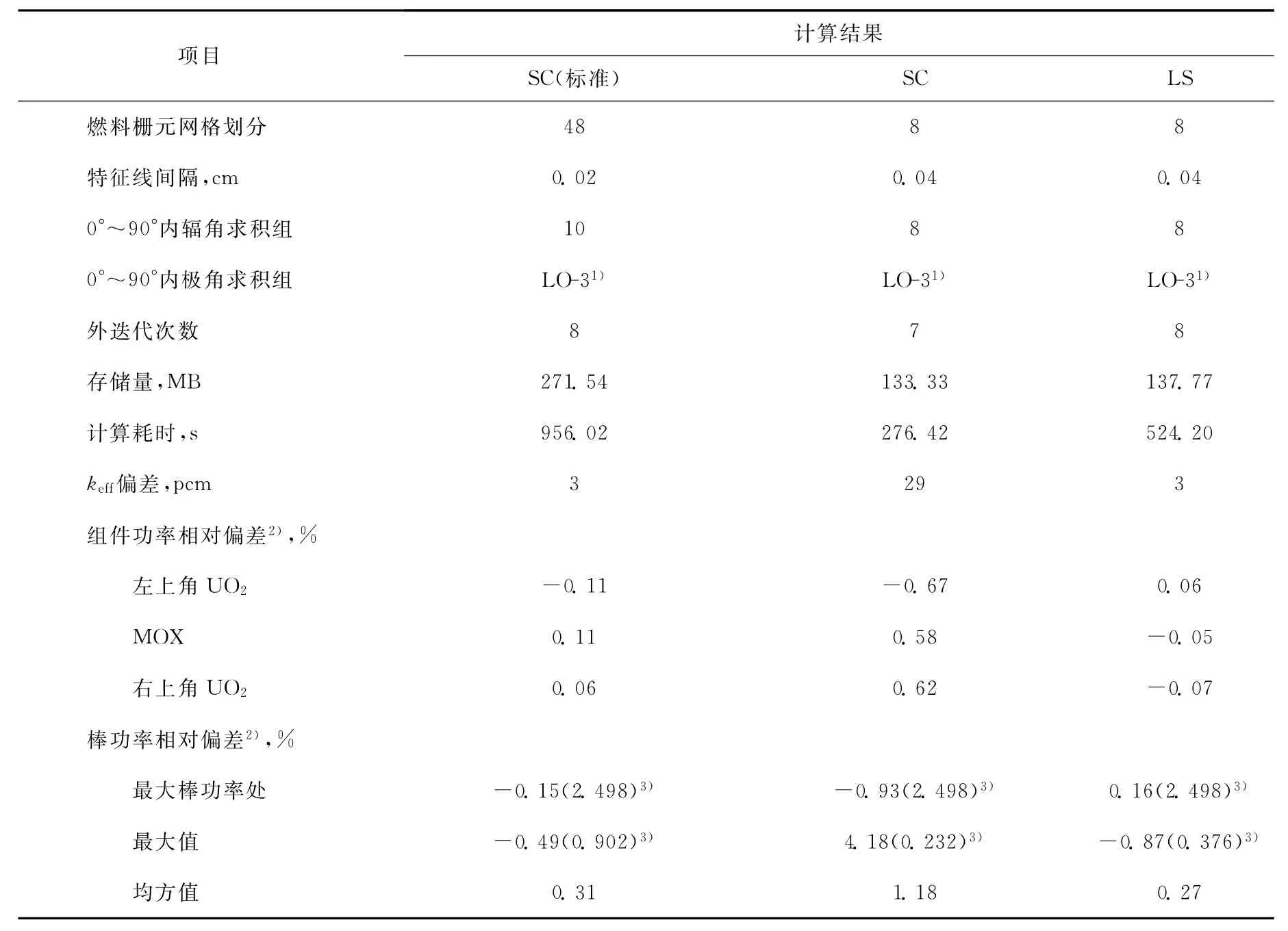
表1 C5G7-MOX 2D问题特征线法平源近似和线性源近似结果比较Table 1 Performance comparisons between SC and LS schemes for C5G7-MOX 2Dproblem
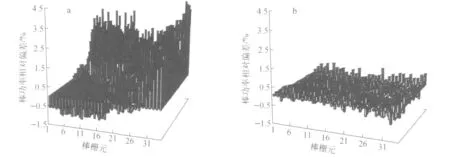
图4 粗控制参数下平源近似(a)和线性源近似(b)的精细棒功率相对偏差分布Fig.4 Comparison of pin power relative deviation distributions between SC scheme(a)and LS scheme(b)with coarse parameters
各种材料的69群宏观截面由IAEA 69群截面库经DRAGON程序[4]计算产生。该问题的参考解(keff和精细棒功率分布)由多群蒙特卡罗程序 MCMG[8]给出。为获得可靠的计算结果,在MCMG计算过程中每代投入的粒子数为160 000,总共计算1 200代,其中前100代不参与统计。
在计算该问题时,将特征线法的标准控制参数设定为:1/8卦限内辐角数目为8、极角数目为3,平均相邻特征线间的间隔为0.03cm,每燃料栅元内的网格数为40,靠近燃料棒的4列反射层栅元采用5×5等分、再外面的反射层用3×3等分。该标准参数下的数值结果由PEACH的平源近似步特征线法模型给出。
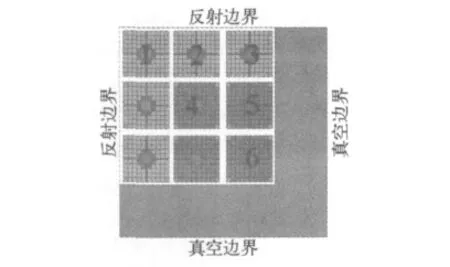
图5 自定义沸水堆小堆芯问题布置Fig.5 Configuration of self-defined BWR mini-core problem
为了展示本工作提出的线性源特征线法的优越性,将控制参数放松为:1/8卦限内辐角数目为4、极角数目为2,平均相邻特征线间的间隔为0.07cm,每燃料栅元内的网格数为12,反射层栅元网格划分与标准参数时相同。
表2列出程序PEACH平源近似模块和线性源近似模块针对该问题与参考解相比较的偏差。由表2可知,一旦平源近似网格划分较大时,平源近似特征线法模块的精度将受影响,针对该问题,keff的偏差为-140pcm、最大棒功率的相对偏差可达3.54%。但在相同控制参数的情况下,线性源近似特征线法模块可给出与标准参数下精度相当的计算结果。另外,从计算机的耗时和存储量两方面来看,线性源近似特征线法模块不到标准参数下平源近似特征线法模块的1/2,再次证明线性源近似特征线法具备较明显的优势。
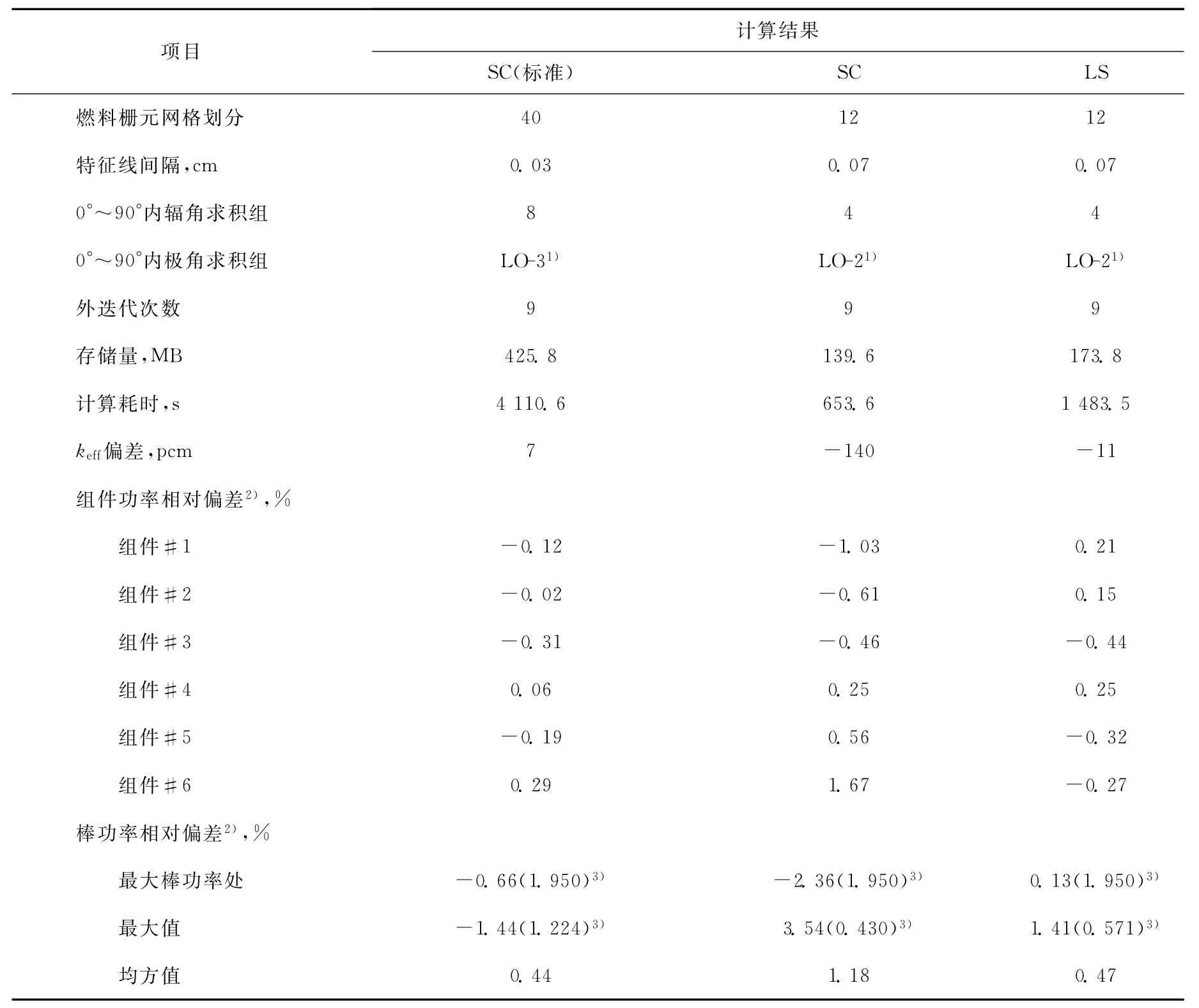
表2 沸水堆小堆芯问题特征线法平源近似和线性源近似结果比较Table 2 Performance comparisons between SC and LS schemes for BWR mini-core problem
3 结论
本工作提出一种基于坐标投影法的线性源特征线法跟踪计算模型,提出了迭代求解过程中相关负中子源分布的修正方法,并将该模型成功加入程序PEACH中。通过C5G7-MOX 2D基准题和自定义沸水堆小堆芯问题的数值验算结果表明,本工作提出的线性源近似特征线法模型在相同计算精度的前提下,占用更少的系统内存和运行时间,值得在中子输运方程的特征线解法领域中推广。
本工作是在上海交通大学赵荣安教授和张少泓副教授指导下完成的,在此对二位导师表示最诚挚的感谢。
[1]SMITH K S,RHODES J D.Full-core 2-D LWR core calculations with CASMO-4E[C/CD]∥Proceedings of PHYSOR 2002.Seoul,Korea:[s.n.],2002.
[2]WEMPLE C A, GHEORGHIU H N M,STAMM′LER R J J,et al.Recent advances in the HELIOS-2lattice physics code[C]∥Proceedings of PHYSOR 2008.Interlaken,Switzerland:[s.n.],2008.
[3]NETWON T,HOSKING G,HUTTON L,et al.Developments within WIMS10[C]∥Proceedings of PHYSOR 2008.Interlaken,Switzerland:[s.n.],2008.
[4]MARLEAU G,HÉBERT A,ROY R.A user’s guide for DRAGON,IGE-174[R].[S.l.]:Ecole Polytechnique de Montréal,2007.
[5]汤春桃,张少泓.以栅元为模块进行特征线跟踪的中子输运方程解法[J].核动力工程,2009,30(4):32-36.TANG Chuntao,ZHANG Shaohong.Study on method of characteristics based on cell modular ray tracing[J].Nuclear Power Engineering,2009,30(4):32-36(in Chinese).
[6]汤春桃,张少泓.CMFD加速在特征线法输运计算中的应用[J].核动力工程,2009,30(5):8-12.TANG Chuntao,ZHANG Shaohong.Application of coarse-mesh finite difference acceleration in transportation calculation by method of characteristics[J].Nuclear Power Engineering,2009,30(5):8-12(in Chinese).
[7]LEWIS E E,SMITH M A,TSOULFANIDIS N,et al.Benchmark specification for deterministic 2-D/3-D MOX fuel assembly transport calculations without spatial homogenisation (C5G7-MOX),NEA/NSC/DOC(2001)4[R].USA:OECD/NEA,2001.
[8]DENG L,XIE Z S,ZHANG J M.A 3-D multigroup P-3Monte Carlo code and its benchmarks[J].J Nucl Sci Technol,2000,37(7):608-614.

