用Timoshenko梁修正理论研究功能梯度材料梁的动力响应

吴 晓， 罗佑新

(湖南文理学院，常德 415000)

功能梯度材料是基于一种全新的材料设计概念合成的新型复合材料［1－10]，日本科学家于20世纪80年代末年提出了功能梯度材料的概念［11]，即根据具体的要求，选择使用两种不同性能的材料，通过连续平滑地改变两种材料的组织和结构，使其结合部位的界面消失，从而得到功能相应于组织变化而变化的均质材料，最终减小或消除结合部位的性能不匹配因素。功能梯度材料梁的力学性能引起了工程设计人员的极大关注，有关研究功能梯度材料梁的文献都没有确定功能梯度材料梁的中性轴真实位置，而是假设了功能梯度材料梁中性轴位置在距离梁上表面二分之一处，然而一般功能梯度材料仅是功能相应于组织变化而变化的均质材料，功能梯度材料梁中性轴位置不在距离梁上表面二分之一处，这种研究方法显然是具有局限性的。基于上述原因，本文首先确定了功能梯度材料梁的中性轴位置，在此基础上应用Timoshenko梁修正理论建立了功能梯度材料梁的振动方程，讨论了有关因素对功能梯度材料梁动力响应的影响。因为经典Timoshenko梁理论建立的运动方程是时间和空间的四阶微分方程，导致存在两个实频率系。文献［12，13] 对Timoshenko梁的振动方程进行了修正，修改了Timoshenko梁理论的不足之处，证明了Timoshenko梁实际上仅有一个固有频谱。因此，本文采用Timoshenko梁修正理论研究了泡沫铝合金梁的动力特性。

1 振动微分方程

对于功能梯度材料梁，其下侧为金属材料，上侧为陶瓷材料，中间为两种材料组成的混合物。由于金属材料与陶瓷材料的泊松比相近，可令它们的泊松比均为μ。设金属材料的弹性模量、剪切弹性模量、密度分别为Em、Gm、ρm，陶瓷材料的弹性模量、剪切弹性模量、密度分别为Ec、Gc、ρc，则梁内任一点的弹性模量、剪切弹性模量、密度分别为:

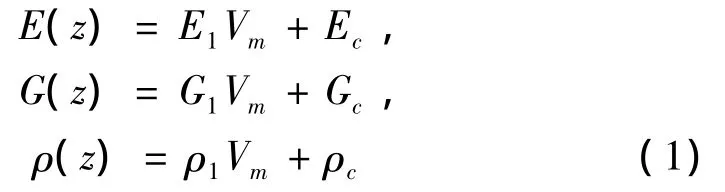
式中，E1=Em－Ec，G1=Gm－Gc，ρ1=ρm－ρc，Vm为金属材料组分的体积比例系数。

假设坐标原点建立在功能梯度材料梁的中性轴上，设功能梯度材料梁中金属材料组分的体积比例系数为梁厚方向坐标z的幂函数为:

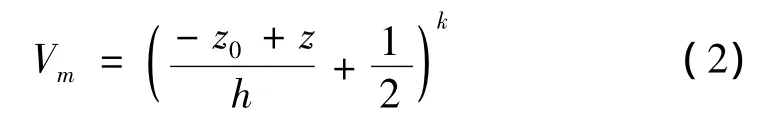
式中，k为梯度指数，z0为梁中性轴真实位置与有关文献假设距梁上表面二分之一处的中性轴之间的距离。

根据Timoshenko梁修正理论假设φ为梁截面弯曲转角，y为梁的挠度，可知功能梯度材料梁的应力表达式为:

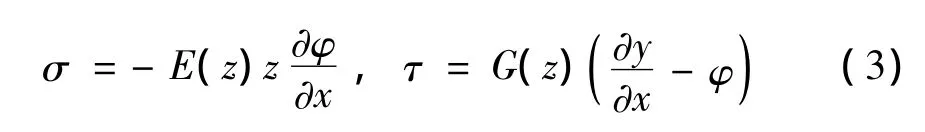
功能梯度材料纯弯曲时横截面内力应满足下式:

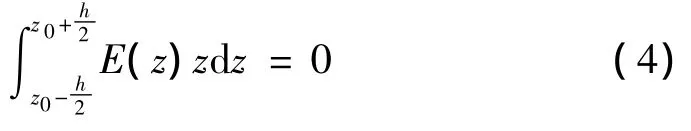
把式(1)、式(2)代入式(4)中可以得到:

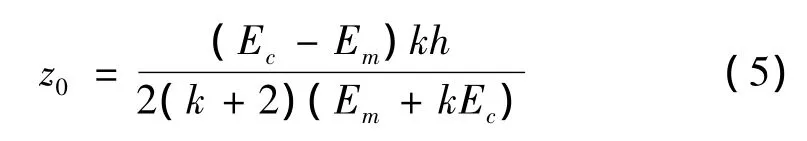
利用式(3)可得功能梯度材料梁的弯矩、剪力表达式为:

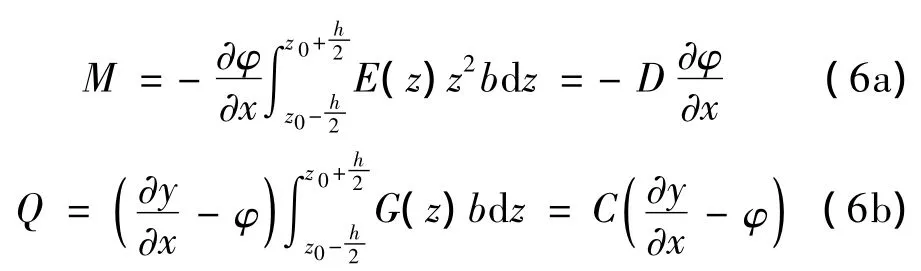
式中，μ为剪切因子，

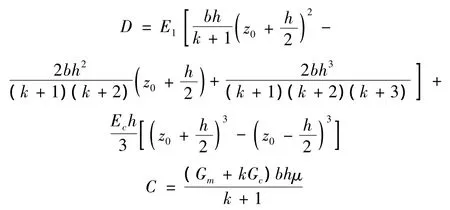
对于图1所示在横向动荷载作用下的功能梯度材料梁，参阅文献［12－14] 可知功能梯度材料梁采用Timoshenko梁修正理论得到振动微分方程为:

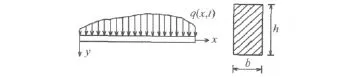
图1 功能梯度材料梁Fig.1 Beam with functionally graded materials

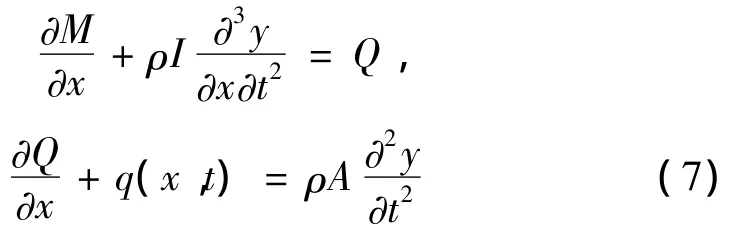
式中:

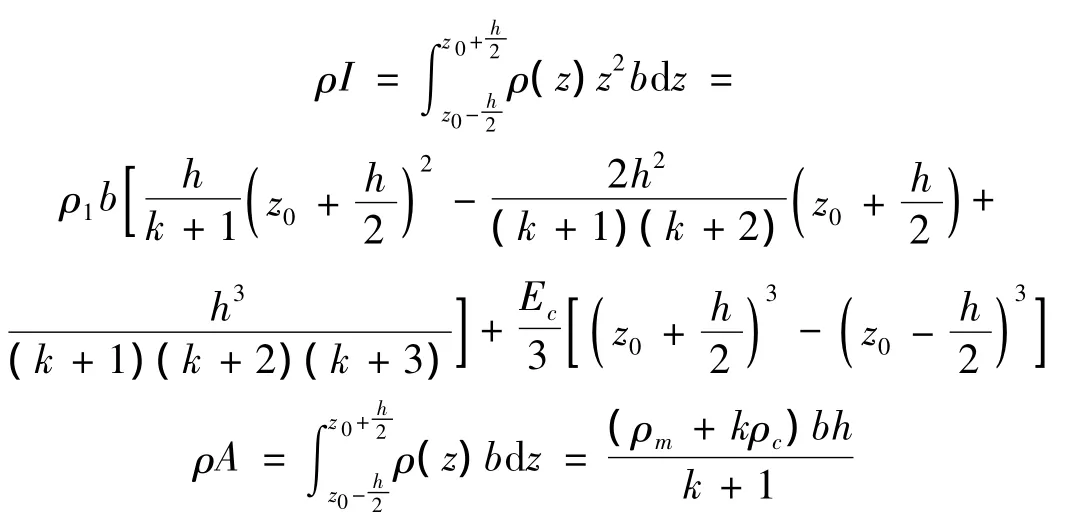
把式(6)代入式(7)中可以得到:

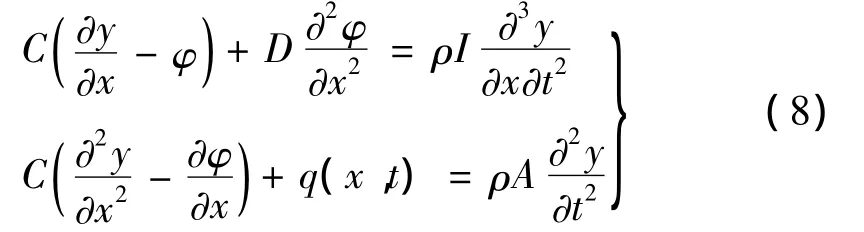
把式(8)解耦后可得修正Timoshenko梁振动方程为:

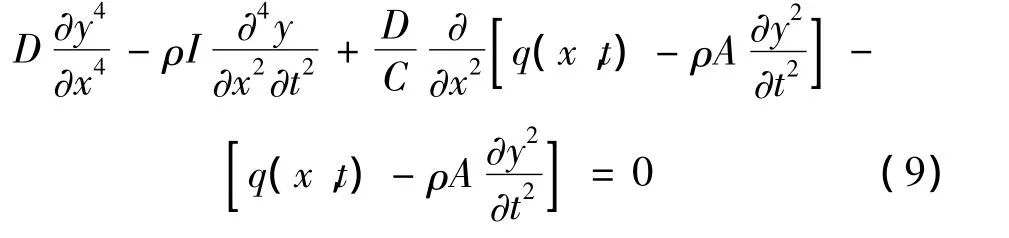
2 功能梯度材料梁动力响应

2.1 自由振动的解

令功能梯度材料梁的自由振动位移及外载荷分别为:

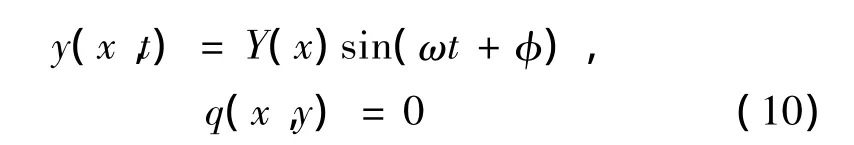
把式(10)代入式(9)中可以得到:

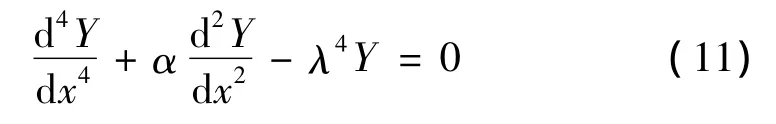
式中，

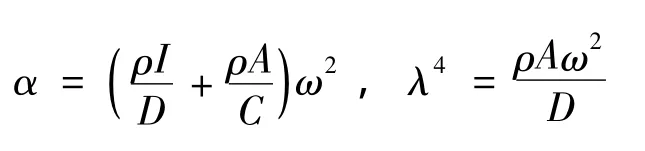
由式(11)可以求得功能梯度材料梁振型函数为:

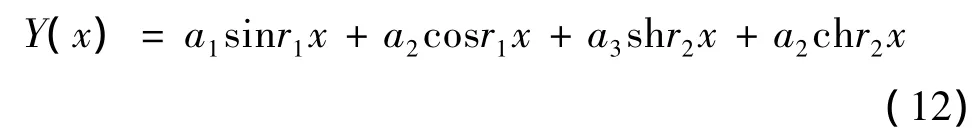
式中:

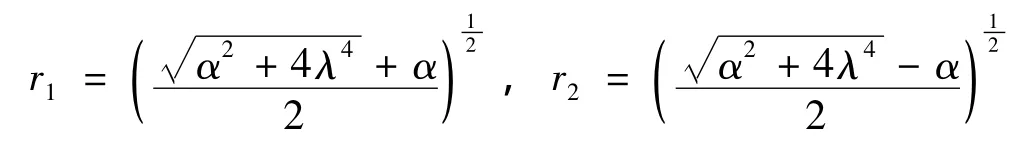
以简支梁为例，可知功能梯度材料梁的边界条件为:

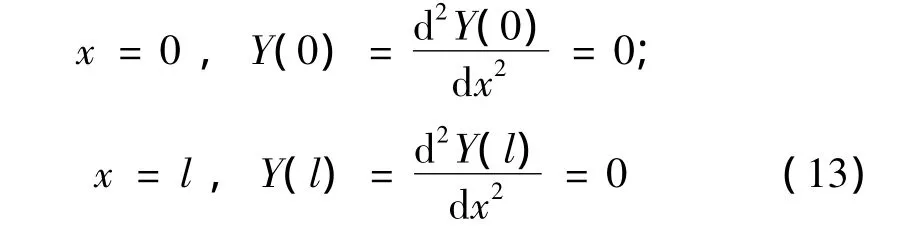
利用式(12)、式(13)可以求得功能梯度材料梁的自振频率为:

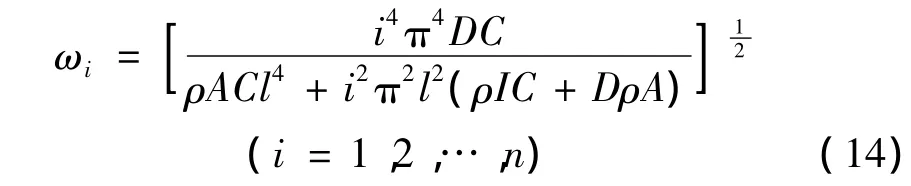
所以，功能梯度材料简支梁的振动位移为:

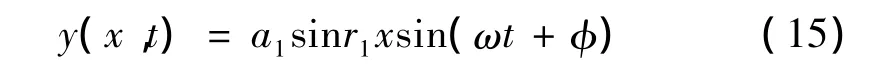
2.2 强迫振动的解

令式(9)的解为:

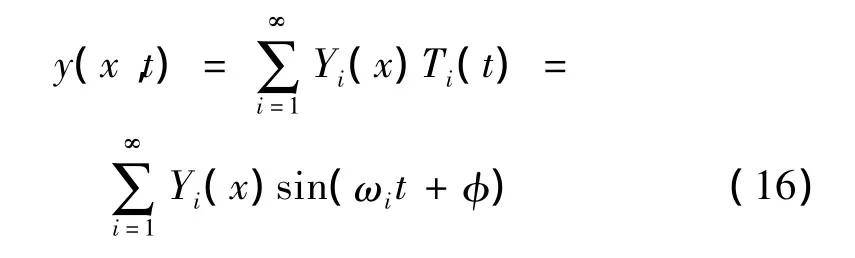
假设式(11)在简支梁的边界条件下，对应于ωi和ωj的两个振型函数为Yi(x)和Yj(x)，把式(16)代入式(11)中，于是有:

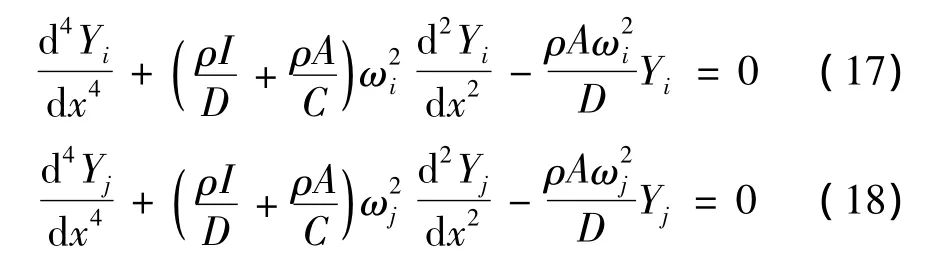
将式(17)乘以Yj(x)、式(18)乘以Yi(x)，然后把所得的两个乘式相减，再沿梁全长积分，注意在积分式中代入铰支座边界条件，即得所需要的正交性方程式:

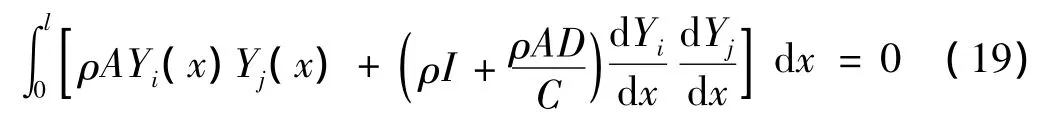
把式(16)及简支梁振型函数代入式(9)中并应用式(19)可以得到:

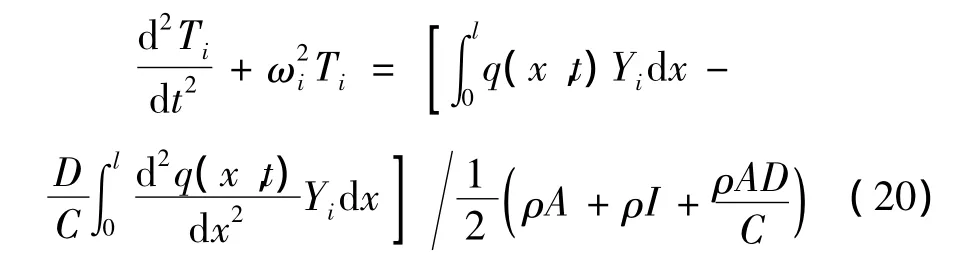
假设分布荷载q(x，t)在时间上与空间上可分离，可令:

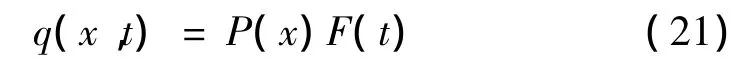
把式(21)代入式(20)中积分可得:

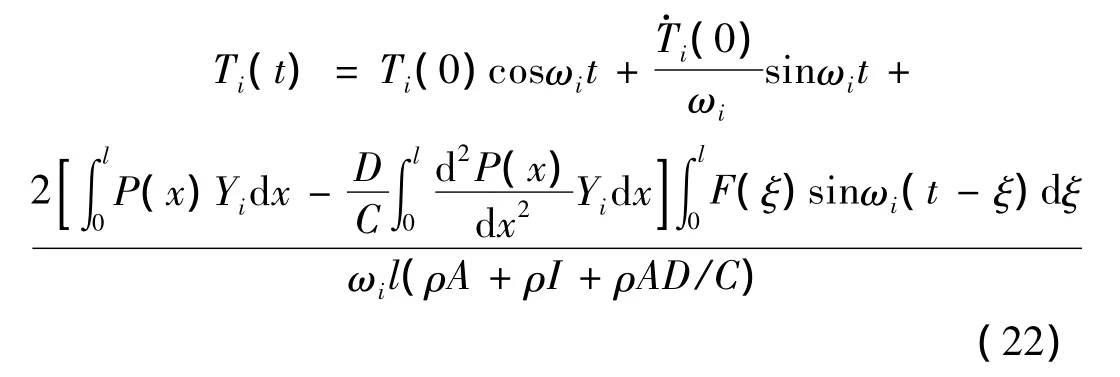
设功能梯度材料梁的初始条件为:

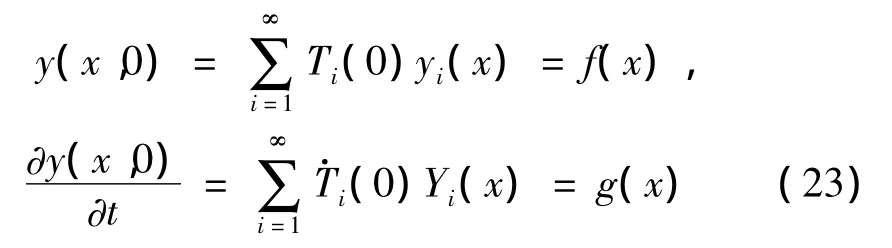
由式(23)可以确定:

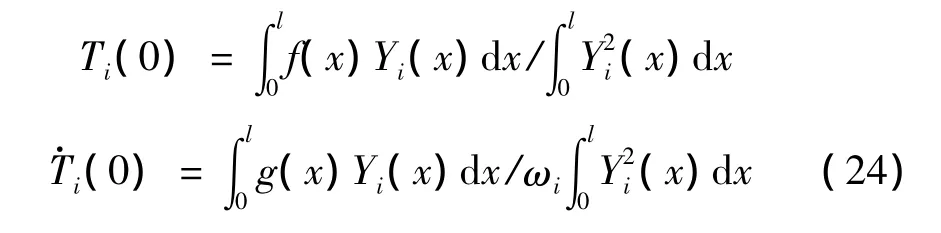
若作用在梁上的外扰力为沿梁长为均匀分布的简谐干扰力 q(x，t)=q0sinΩt，利用式(22)可以求得:

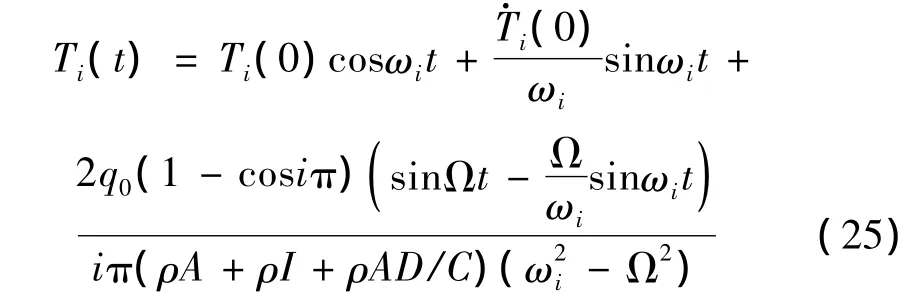
若在简支梁x=l0处作用有一简谐干扰力P0sinΩt，则有 q(x，t)=P0δ(x － l0)，利用式(22)可以得到:

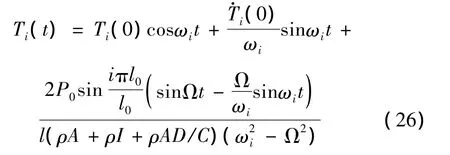
3 算例分析及讨论

为了分析简支功能梯度材料梁的动力特性，取梁长 l=1 m，b=0.22 m，h=0.27 m，l0=0.5 m，Ω =8 rad/s。金属材料的弹性模量、剪切弹性模量、密度分别为 Em=70 GPa、Gm=26.92 GPa、ρm=2.7 ×103kg/m3。陶瓷材料的弹性模量、剪切弹性模量、密度分别为Ec=380 GPa、Gc=146.15 GPa、ρc=2.5 × 103kg/m3、μ =5/6。

分别采用有限元和本文方法计算简支功能梯度材料梁固有频率值，计算结果如表1所示。在图2—图5中假设初始条件 Ti(0)、(0)皆等于零时，采用及式(25)、式(26)进行计算得到了简支功能梯度材料梁中点处的动力曲线。具体计算结果可见表1及图2—图5。

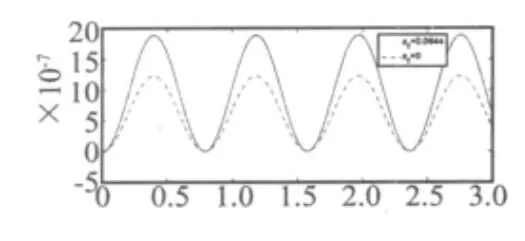
图2 动力响应曲线(q0=1 000 N/m，k=0.5)Fig.2 The dynamic responsecurve(k=0.5)

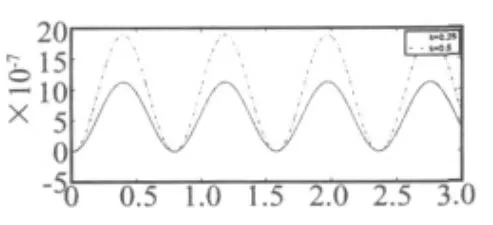
图3 动力响应曲线q0=1 000 N/mFig.3 The dynamic response curve

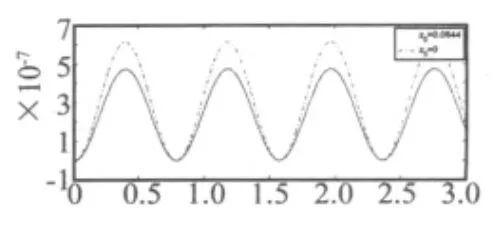
图4 动力响应曲线(P0=1 000 N，k=0.5)Fig.4 The dynamic response curve(k=0.5)

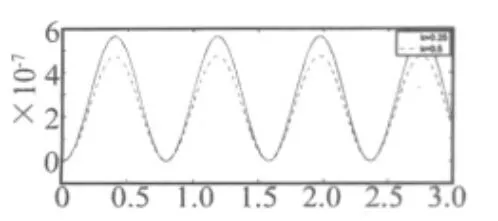
图5 动力响应曲线(P0=1 000 N)Fig.5 The dynamic response curve

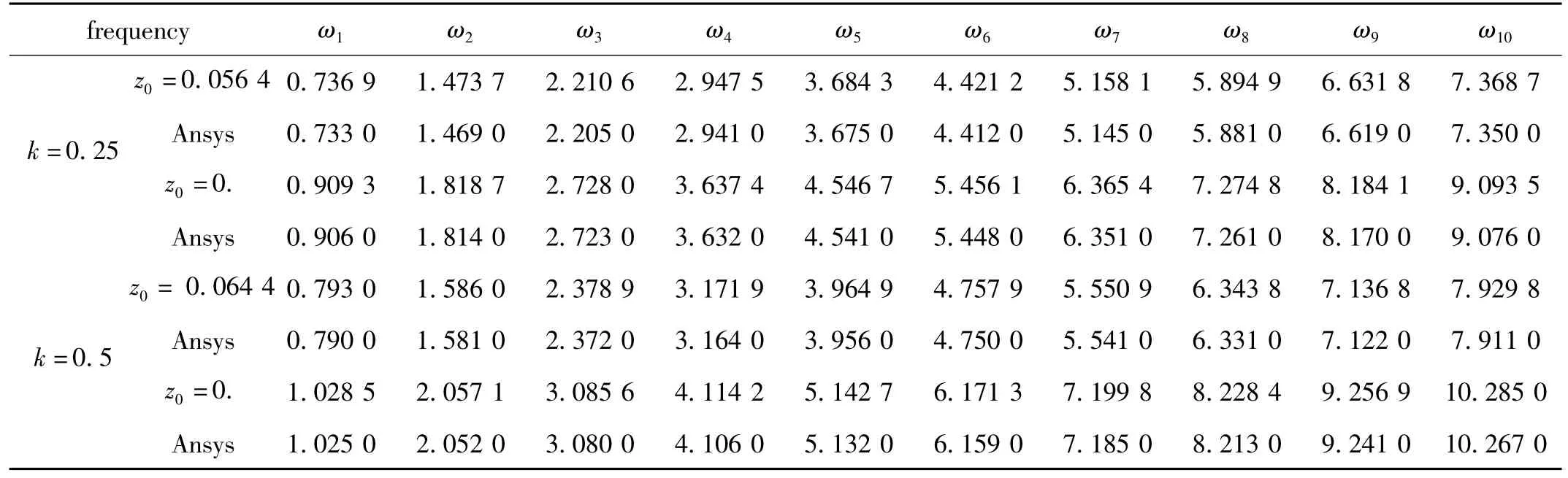
表1 简支功能梯度材料梁固有频率ωi(rad/s)Tab.1 Natural frequency of simply supported beam with functionally graded materials

由表1可以知道采用Timoshenko梁修正理论计算的固有频率与有限元法计算的固有频率非常接近。这说明采用Timoshenko梁修正理论计算梁的固有频率是比较合理的。

由表1及图3、图5可以看出，随着梯度指数k增大功能梯度材料梁固有振动频率将变大。而随着梯度指数k增大功能梯度材料梁在均布载荷作用下动力响应曲线的幅值将变大、在集中载荷作用下动力响应曲线的幅值将变小。

由表1及图2、图4还可知道，如按有关文献不确定功能梯度材料梁中性轴的真实位置，而是假设功能梯度材料梁相对于中性面具有几何和弹性对称，来研究功能梯度材料梁的固有振动及动力响应，得到的固有频率将偏大。同时确定功能梯度材料梁中性轴的真实位置后，在均布载荷作用下功能梯度材料梁动力响应曲线的幅值将偏大，而在集中载荷作用下功能梯度材料梁动力响应曲线的幅值将偏小。所以，功能梯度材料梁中性轴位置对功能梯度材料梁的固有振动及动力响应有较大的影响，这一点由由表1及图2～图5看出。

4 结论

由以上分析可以得到以下结论:

(1)采用Timoshenko梁修正理论计算梁的固有频率是比较合理的。

(2)随着梯度指数k增大功能梯度材料梁固有振动频率将变大。而随着梯度指数k增大功能梯度材料梁在均布载荷作用下动力响应曲线的幅值将变大、在集中载荷作用下动力响应曲线的幅值将变小。

(3)功能梯度材料梁中性轴位置对功能梯度材料梁的固有振动及动力响应有较大的影响。

［1] Zhong Z，Yu T.Vibration of a simply supported functionally graded piezoelectric rectangular plate［J] .Smart Mater Struct，2006，15:1404 －1412.

［2] Zhong Z，Shang E T.Three－ dimensional exact analysis of a simply supported functionally gradient piezoelectric plate［J] .Int JSolids Struct，2003，40(20):5335 －5352.

［3] 尚尔涛，仲 政.功能梯度热释电材料平板柱形弯曲问题的精确解［J] .应用力学学报，2003，20(4):122 －125.

［4] Chen W Q，Ding H J.On free vibration of a functionally graded piezoelectric plates ［J] .Acta Mechanica，2002，153－207.

［5] Wu X H，Chen C Q，Shen Y P，et al.A high order theory for functionally graded piezoelectric shells［J] .Int J Solids Struct，2002，39(20):5325 －5344.

［6] 王铁军，马连生，石朝锋.功能梯度中厚圆/环板轴对称弯曲问题的解析解［J] .力学学报，2004，36(3):348 －353.

［7] 马连生，赵永刚，杨静宁.功能梯度圆板的轴对称非线性分析——大挠度问题［J] .兰州理工大学学报，2004，30(6):139－142.

［8] 马连生，赵永刚，杨静宁.径向压力作用下功能梯度圆板的过屈曲［J] .兰州理工大学学报，2006，32(4):158 －161.

［9] 沈惠申.功能梯度复合材料板壳结构的弯曲、屈曲和振动［J] .力学进展，2004，34(1):53 －60.

［10] 刘 进，武兰河，张晓炜.功能梯度材料板的弯曲问题［J] .石家庄铁道学院学报，2003，16(2):1 －5.

［11] 陈 镕，郑海涛，薛松涛，等.无约束Timoshenko梁横向冲击响应分析［J] .应用力学和数学，2004，25(11):1195－1201.

［12] 陈 镕，万春风，薛松涛，等.Timoshenko梁运动方程的修正及其影响［J] .同济大学学报(自然科学版)，2005，33(6):711－715.

［13] 陈 镕，万春风，薛松涛，等.无约束修正Timoshenko梁的冲击问题［J] .力学学报，2006，38(2):262 －268.