电磁喇叭分段线性振动响应及其声学特性的研究
郭继峰, 任万滨, 翟国富, 赵宏伟
(1.哈尔滨工业大学 军用电器研究所,哈尔滨 150001;2.东北林业大学,哈尔滨 150040;3.哈尔滨工业大学 固泰电子有限责任公司,哈尔滨 150060)
电磁喇叭是一类将电能转变为声音的换能器件,广泛用于具备直流电源的水陆交通工具中。作为警告信号用的喇叭现已成为各类交通工具安全系统中不可或缺的关键元器件。低成本、长寿命、高可靠性和环境适应性已成为喇叭的未来发展方向[1]。
交流电动式扬声器及电动式耳机的设计问题与失效模式现已得到广泛关注[2~4]。电磁喇叭与其不同点在于,运动零件动铁心、动触头、静触头间具有可分合接触特点,导致结构动力学系统具有多自由度分段线性的特征,属于一类典型的含间隙的碰撞振动系统[5]。另外其电磁激振力亦与动铁心、动静触头的振动响应相关,具有显著的时变脉动性。电磁喇叭电磁系统与运动系统参数的合理确定将直接关系到膜片振动稳态响应,且最终影响其发声特性。国内学者更多地关注于电磁喇叭膜片零件对其发声特性的影响,如叶郁文对膜片横向振动频率与发声特性的关系进行了研究[6],季强研究了膜片振动碎裂的原因及改进的工艺设计[7]。
本文根据电磁喇叭结构特征建立了其工作过程中时变电磁力激励条件下动铁心与膜片构成的分段线性振子动力学模型,应用数值积分方法分析了电磁喇叭振动响应特性。进而根据所得到的稳态振动幅值与频率应用ANSYS软件仿真了电磁喇叭的声学特性,并重点研究了喇叭中触头压力及间隙参数对振动响应及发声特性的影响规律。
1 数学模型
1.1 结构特点
电磁喇叭整体结构主要由电磁系统、接触系统和振动发声部分组成。其中电磁系统包括动铁心、静铁心、激磁线圈以及钢板外壳等;接触系统由动触头、动簧片、静触头、静簧片和绝缘膜片组成。膜片和号筒则构成了振动发声部分,如图1所示。

图1 电磁振动喇叭平面结构示意图Fig.1 schematic sketch of electromagnetic horn planer structure
线圈通入直流电产生磁场,电磁力吸引动铁心带动膜片向下运动,动铁心继而推动常闭触头分断,激磁电流减小至零。当电磁吸力低于动簧片与膜片所构成的机械结构反力时,动铁心依靠动簧片与膜片的回弹力自下而上返回运动,触头即又恢复闭合状态导通激磁线圈电流,吸引动铁心重复上述作用过程。此过程中膜片在周期性外力作用下产生简谐振动,引起周围空气产生波动,通过号筒传播即为喇叭的鸣叫声。
1.2 电磁模型
电磁喇叭的电流和电压具有周期性的特点,线圈与触头间的串联关系使燃弧阶段与熄弧阶段电压平衡方程为:
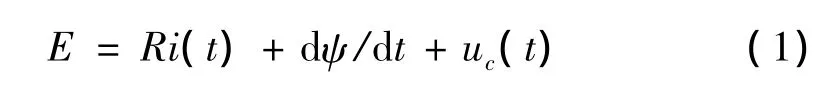
式中:E为电源电压;i为回路电流;R为线圈电阻;ψ为线圈磁链;uc为电弧电压。
考虑到线圈电流与动铁心位移的时变性,式(1)中的线圈磁链变化率可改写为:
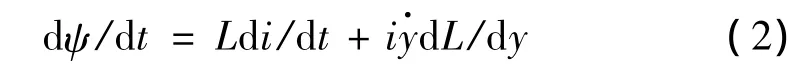
则振动过程中动铁心的时变电磁力可表示为:
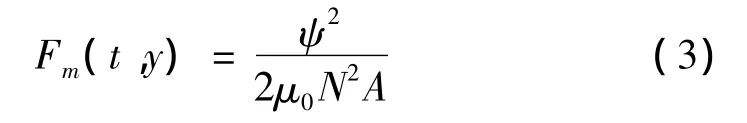
式中:N为线圈匝数;A为截面积。
1.3 分段线性振子模型
将动铁心、静触簧、动触簧分别等效为集中质量M1、M2、M3,k1、k2、k3分别为振动膜片、静触簧、动触簧的等效刚度。c1、c2、c3分别为振动膜片(含空气)、静触簧、动触簧的等效阻尼。考虑到动铁心与动触簧间、静触簧与动触簧间具有的可分合接触特征,因此以kj1、kj2等效接触刚度描述其间的接触状态。且静触簧与动触簧间接触压力为F0,满足:
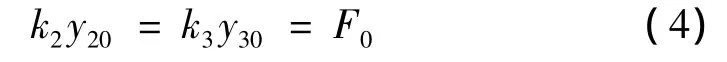
式中y20、y30分别为静触簧和动触簧的初始变形量。
规定竖直向上为正方向,根据结构运动特征可得振动系统力学模型,如图2所示。
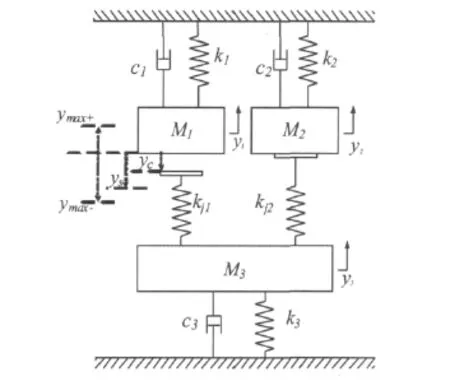
图2 电磁振动喇叭等效力学模型Fig.2 Equivalent mechanical model
为分析方便,引入下列动铁心位移特征量辅助描述喇叭振子模型
yc为M1与M3初始间隙;
ys为使动触头与静触头分离的动铁心位移;
ymax+为动铁心竖直向上的最大位移;
ymin-为动铁心竖直向下的最大位移。
当ymax+<y1<yc时,喇叭振子模型可写为:

式中Fm为电磁驱动力,与时间和动铁心位移参数直接相关。此时电磁喇叭动作对应为单自由度系统模型。
当yc<y1<ys时,动铁心与动触簧、静触簧构成三自由度系统,振子模型可改为:
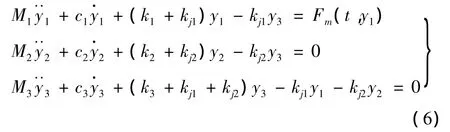
当ys<y1<ymax-时,动触簧与静触簧脱离接触,振子退化为两自由度系统,模型可改写为:
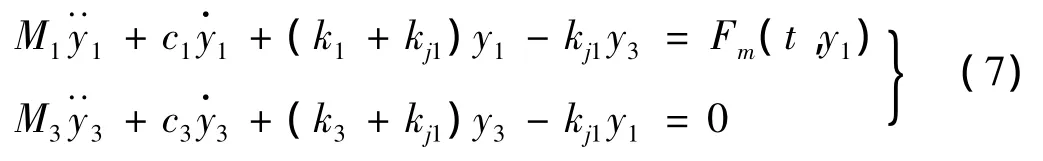
式(5)-式(7)表明电磁喇叭周期振动数学模型具有质量—弹簧—阻尼分段线性的特征,属于典型的非线性结构动力学问题。其周期振动过程中动铁心、动静触点的振动响应不仅与本身结构特征参数相关,同时与电磁系统结构参数及所能提供的驱动力直接相关。
2 振动响应数值计算
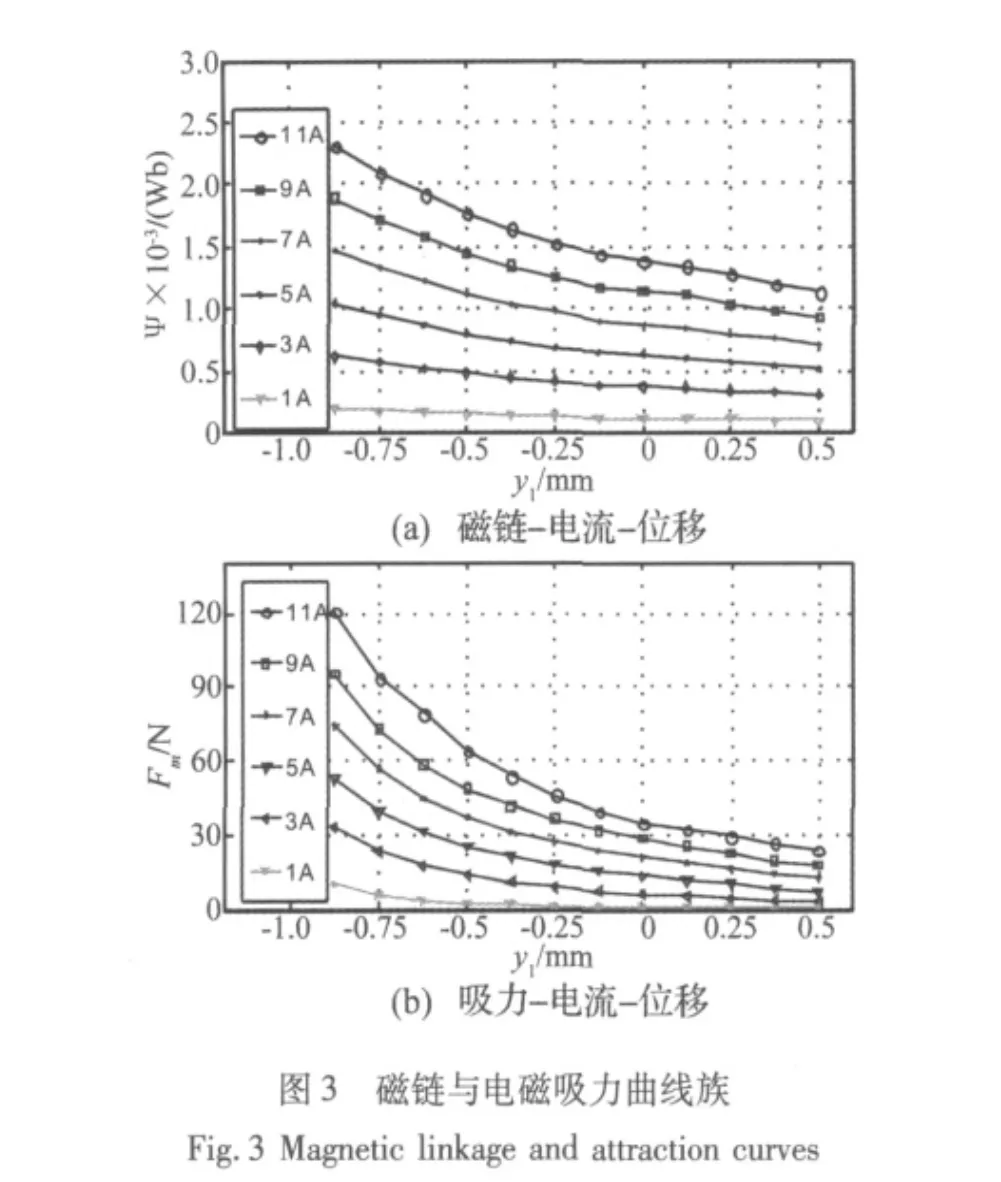
选取一个额定电压为12 V的蜗牛形电磁喇叭作为试验对象,线圈电阻0.97Ω,由电磁场有限元分析软件FLUX求解磁气隙在工作范围内,电流由零至稳定状态间磁链曲线族ψ(y1,i)与电磁吸力曲线族Fm(y1,i)(如图3所示),并以此作为振子激励源。
选取电磁喇叭基本参数为 M1=22.35 g,M2=M3=0.07 g,k1=223.7 N/mm,k2=1 788.9 N/mm,k3=6.1 N/mm,c1=11.7 N·s/m,c2=c3=0.001 N·s/m,kj1=kj2=107N/m,f0=3 N,yc=0.02 mm。电磁喇叭振动响应计算流程如图4所示,电磁模型采用龙格-库塔法计算取Δt1=1μs,振子模型应用中心差分法计算取Δt2=1μs。
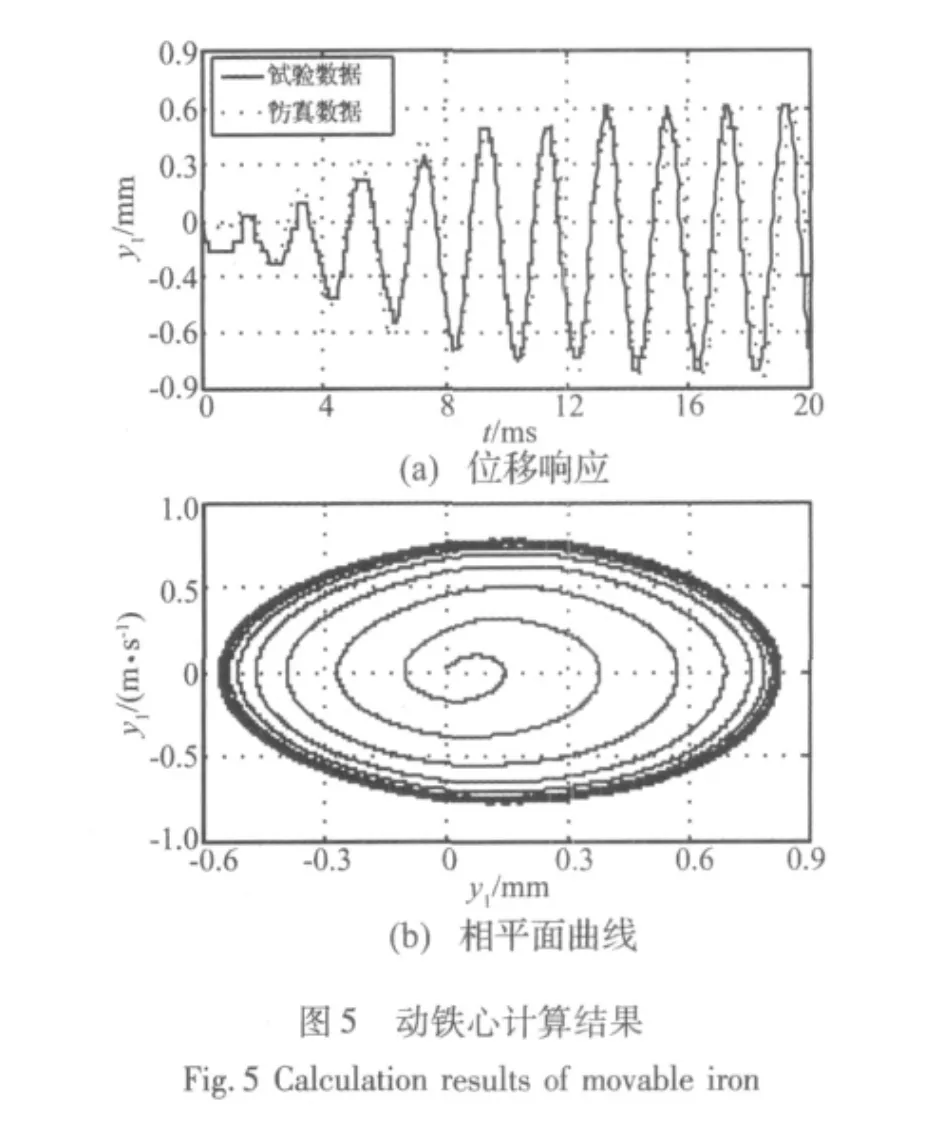
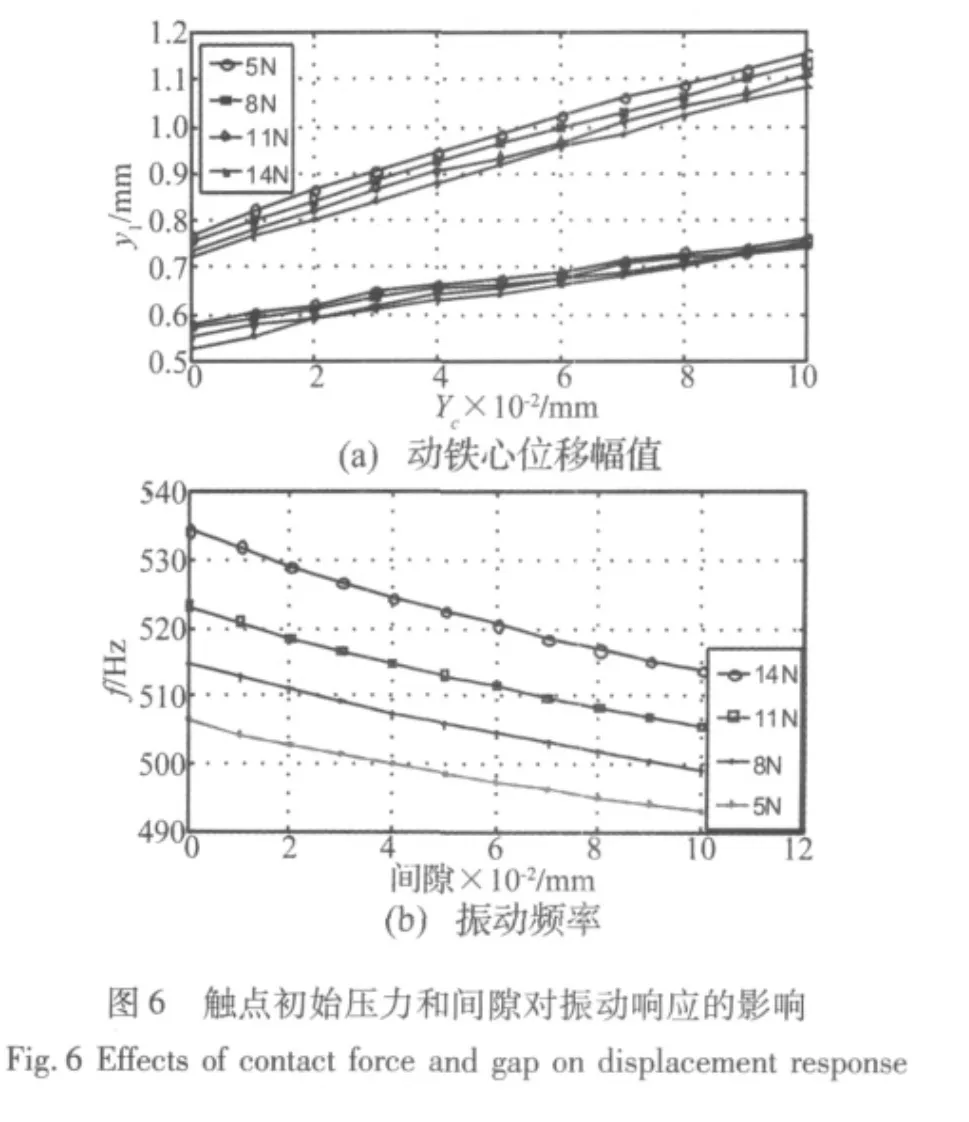
设定仿真时间,计算所得动铁心振子响应如图5所示。经过起动与过渡过程达到稳定振动,过平衡位置21次,振动频率f=496.4 Hz,且振子位移响应幅值存在不对称现象,即 ymax+=0.56 mm,ymax-=0.83 mm。同时应用高速数字摄像机(Phantom V7.3)记录动铁心的全部运动过程,可见很好地验证了所建模型的准确性。改变触头压力与间隙条件下的动铁心位移响应如图6所示,可见动铁心稳态响应幅值ymax+、ymax-均具有随触头压力F0的增大而减小,随间隙yc的增大而增大。上述算例条件下电磁喇叭系统均为稳定性振动,且增大F0和减小yc可使动铁心振动频率增大。
3 声学特性
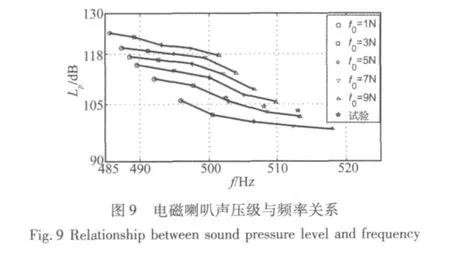
电磁喇叭声压级和频率是喇叭性能的两项重要指标,我国汽车用电磁喇叭通常规定声压级为105 dB-118 dB,频率为 500 ±10 Hz[8]。前文所述动铁心带动膜片进行上下振动,经过号筒可发声传播。考虑到号筒形状的复杂性,本文采用商用有限元软件ANSYS建立包括膜片、壳体、号筒、号筒中气柱的几何模型,仿真过程中应用的单元类型及材料如表1所示。以动铁心位移响应波形加载至动铁心底部,将膜片周围设为固定边界(如图8所示)。按照文献[8] 中的试验条件完成仿真其在消音室中的声压级分布,得到距喇叭口2 m处的声压级,图9为得到的触头压力[1,9 N] 与间隙[0,0.1 mm] 装配条件下,电磁喇叭声压级与频率变化的特性曲线。实验测试该喇叭在yc=0.02 mm条件下触头压力为5 N时频率为503 Hz,声压级为107 dB;触头压力为7 N时频率为508 Hz,声压级为109 dB;触头压力为9N时频率为513 Hz,声压级为103 dB。计算结果较测试结果均偏低,仿真中未考虑结构与声的耦合是产生误差的主要原因。
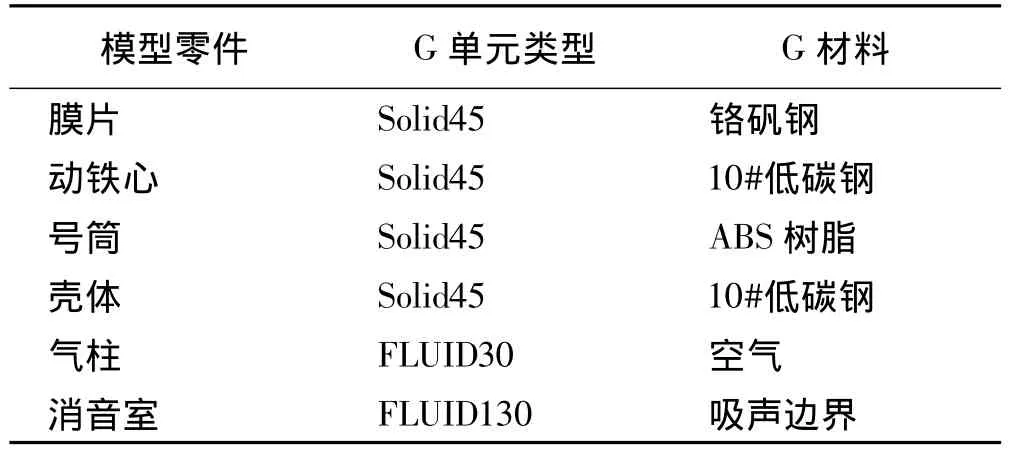
表1 喇叭单元类型与材料Tab.1 Element type and material of horn

4 讨论
综合上述计算结果可知,增大触头初始压力F0,可增加常闭触簧系统的固有频率,抑制了动铁心碰撞动触头的位移响应,因此将减弱膜片的振动幅值,同时减弱喇叭发声声压级。所引起的动铁心与动触头碰撞次数增加,因而电磁喇叭发声频率增加。另外,增大间隙yc相应地增加了膜片的振动幅值,增强喇叭发声声压级。同时减少了其与动触头的碰撞次数,因而电磁喇叭发声频率降低。可见,电磁喇叭的稳态运动及其发声与否与触头初始压力和间隙等装配参数关系密切,两者的合理配合是达到电磁喇叭发声要求的充要条件。由图9可见,不同F0和yc的配合条件下,电磁喇叭稳态振动的声压级与频率两项性能指标呈负相关性。
5 结论
(1)电磁喇叭是一类分段线性的碰撞振动系统,本文所建立的数学模型及提出的振动响应分析方法与声学仿真方法完全适用于该问题的动力学特性与声学特性的研究。
(2)电磁喇叭具有机-电-磁耦合特征,激振力与系统位移响应相关,具有脉动性。系统振动位移响应具有频率稳定、幅值不对称的特点。
(3)触头初始压力与间隙是影响电磁喇叭振动响应与发声特性的关键参数,减小触头压力、增大间隙可增强喇叭声压级,降低发声频率;增大触头压力、减小间隙可减弱喇叭声压级,提高发声频率。
[1] 郭继峰,任万滨,翟国富.汽车电喇叭的技术发展[J] .机电元件,2010,30(1):39 -46.
[2] Ravaud R,Lemarquand G,Roussel T.Time-varying nonlinear modeling of electrodynamic loudspeakers[J] . Applied Acoustics,2009,(70):450-458.
[3] Lemarquand G.Ironless loudspeakers[J] .IEEE Transactions on Magnetics,2007,43(8):3371 -3374.
[4] Hsu T S,Poornima K A.Loudspeaker failure modes and error correction techniques[J] .Applied Acoustics,2001,(62):717-734.
[5] 丁旺才,谢建华.碰撞振动系统分岔与混沌的研究进展[J] .力学进展,2005,35(4):513-524.
[6] 叶郁文,王振林,潘钧俊,等.蜗牛式电喇叭膜片振动对声特性的影响研究[J] .振动与冲击,2001,20(2):56-58.
[7] 季 强,蒋伟康,戚方好.汽车喇叭膜片寿命的影响因素分析及其优化设计[J] .振动与冲击,2007,26(5):112 -114.
[8] GB 15742-2006机动车用喇叭的性能要求及试验方法[S] .

