在役桥梁结构损伤位置识别的综合指标方法研究

常 军

(苏州科技学院 土木工程学院，江苏 苏州 215011)

CHANGJun

(School of Civil Engineering，University of Science and Technology of Suzhou，Suzhou，Jiangsu province 215011 China)

许多结构决定了现在社会的发展状况，例如:建筑物、飞机、桥梁、风力涡轮机、海洋平台等。而这些结构在其服务年限内，由于内外环境的共同作用导致其出现连续的损伤积累。实时了解其健康状况，是这些结构能够进一步为社会的发展提供服务的前提条件之一，这一点无疑受到了国内外工程界和学术界的广泛关注，并逐渐成为研究热点之一。桥梁作为国民经济发展的生命线工程，毋庸置疑地受到了社会的广泛关注。目前，包括中国在内的许多国家和地区都在大型桥梁结构上安装了健康监测系统。例如美国的金门大桥、中国的东海大桥和苏通大桥、香港的青马大桥等。作为桥梁健康监测系统组成部分的结构损伤识别是近年来国内外学术界和工程界研究的一大热点。结构损伤会改变结构的物理特性，进而导致其模态特性发生变化，即频率、振型和阻尼比会发生变化。这些指标无疑可作为结构损伤的识别指标。而在实际操作过程中，这些指标并不是理想的，因此如何选择损伤指标是损伤识别的一大难题。近年来，为了能够在结构退化早期就检测出其损伤状况，进而提高结构的预期可靠性和安全性，降低结构维修养护费用，国内外许多专家学者对结构损伤识别进行大量研究，提出一系列损伤识别方法。例如:基于频率变化的损伤识别方法、基于振型变化的结构损伤识别方法、基于曲率模态变化的结构损伤识别方法、基于柔度变化的结构损伤识别方法、模态修正法等。每种方法都有其优缺点，都有其应用前景。基于频率变化的结构损伤识别方法主要是通过损伤前后频率的变化来识别结构的损伤状况，该方法理论基础较清晰，测试简单方便，曾一度受到青睐。但应当指出，该方法在实际应用上也有其限制，例如频率变化对损伤精度要求不敏感，对较严重损伤不敏感等。由于频率是结构的整体性能描述，很难用于具体位置损伤的识别。基于振型改变的损伤识别方法是通过分析损伤前后的振型变化情况来识别结构损伤状况的。基于曲率模态变化识别结构损伤状况方法中，曲率模态实质上是振型的二阶导数，它是振型的一种扩展。该方法之所以受到一定的关注，是因为它与振型相比，对损伤敏感性高［2，3]。

本文提出了一种基于曲率模态和频率变化率的综合指标法。该方法融入了曲率模态对局部损伤灵敏性高和频率方法操作简便、精度高的优点。为了使损伤测试过程中不影响在役桥梁的正常运营，该方法引入了随机子空间方法，随机子空间方法是一种能够识别环境激励下结构模态参数的时域方法。论文所提出的方法可直接应用于在役桥梁损伤识别、桥梁结构健康监测及结构状态评估。

1 系统随机状态空间方法

随机子空间方法是上世纪80年代发展起来的一种用于时域环境下的结构模态参数识别方法。近年来，国内外包括作者在内的许多研究人员对此进行了研究，并发表了许多高水平论文［4－10]，此处不再对该方法进行详细讨论，读者可以查阅相关文献，这里只对其概念进行简单介绍。

随机子空间方法的应用前提是环境激励为白噪声，其均值为0，结构为线性结构，其动力行为可用如下随机状态空间模型描述:

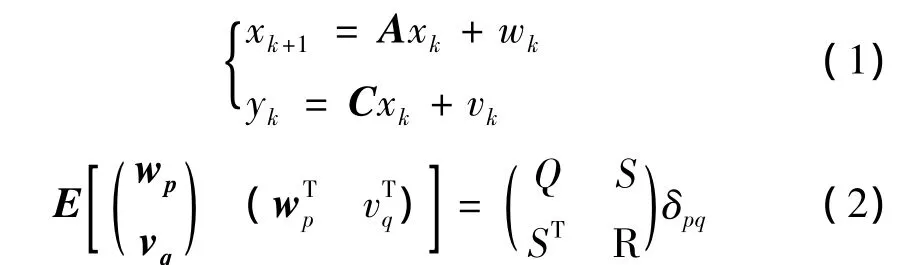
其中，yk∈Rl×1为第l个测点在第 k(k∈N)个采样间隔(Δt)的输出向量为系统的状态向量，n为系统的阶数;A∈Rn×n为状态矩阵;C∈Rl×n为输出矩阵;E为数学期望符号;δpq为 kronecker函数为过程噪声为测量噪声;wk与vk均假定为白噪声，且 E［wk] =0，E［vk] =0。Q∈Rn×n、S∈Rn×l和 R∈Rl×l为噪声序列的协方差矩阵。

随机子空间方法的理论核心是把“将来”输出信息的行空间投影到“过去”输出信息上，投影的结果保留了“过去”的全部信息，并用这些信息预测“将来”的状况。

随机子空间方法中有三个关键数学工具:最小二乘法、奇异值分解(SVD)和QR分解。他们是识别系统状态矩阵的有力工具。可以不严密地说，QR的分解主要用于数据缩减，而SVD则用于剔除干扰。一旦确定系统的数学模型，便可通过特征值分解确定结构模态参数:自振频率、阻尼比和振型。

从理论上讲随机子空间方法是通过投影矩阵的奇异值分解所得到的奇异值确定系统阶次，但由于干扰过多，奇异值确定系统阶次非常困难，在实际应用中常采用稳定图来确定系统的阶次［6－10]。

2 曲率模态方法的基本原理

近年来，国内外许多研究人员都对曲率模态识别结构损伤位置进行了深入研究，并发表了一系列高水平论文［11－13]。

通常，结构的损伤包括结构刚度减小和质量变化两种。但在土木工程领域，结构损伤一般不会导致结构质量发生多大变化，因此，结构损伤识别主要研究结构刚度的降低状况。在采用有限元建模时，通常通过降低结构刚度来模拟其损伤。

在实际操作过程中，结构的曲率模态是通过对现场测试得到结构振型进行差分法近似算出的。具体步骤如下:

根据材料力学的基础知识得到如下关系式:

其中:m为截面位置，Mm为m截面的弯矩，EmIm为m截面的抗弯刚度。Cm为m截面的曲率。

可以看出，曲率和截面的抗弯刚度成反比。因此，由于损伤引起的刚度降低会引起曲率的增加。从理论上讲，在损伤区域，损伤前后的曲率变化是最大的。

例如，一个梁单元，对于一个均匀划分为m段的离散化梁单元，j节点截面的曲率可以表示为:

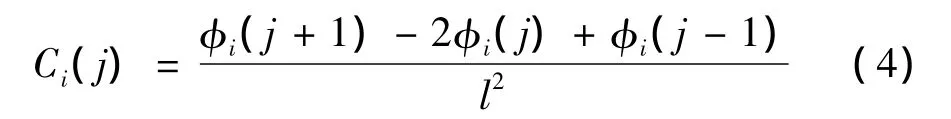
式中:φi(j－1)，2φi(j)，φi(j=1)分别表示第 i阶归一化的振型在j－1，j，j+1点的竖向位移;l为两节点间距离。

3 曲率模态方法的改进

根据结构无阻尼自由振动动力力学方程可推导出第i阶的频率:

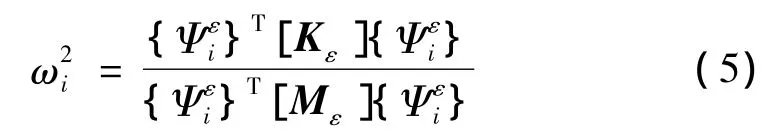
式中，Mε=［B]－T［M] ［B]－1，为质量矩阵;［Kε] =［B]－T［K] ［B]－1，为刚度矩阵;{ε}=［Ψε] {q}，为单元应变向量;［B] 为转换矩阵;［Ψε] 为应变模态;{q}为模态坐标向量。

对i阶振动动力学方程展开并整理得:

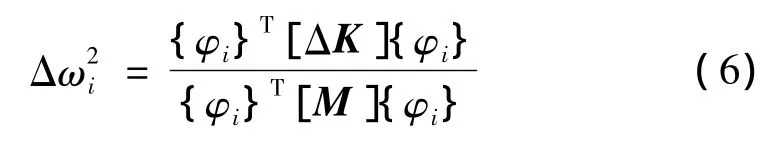
设r(x)是中性面到某点的距离，则该点在x方向的应变为:

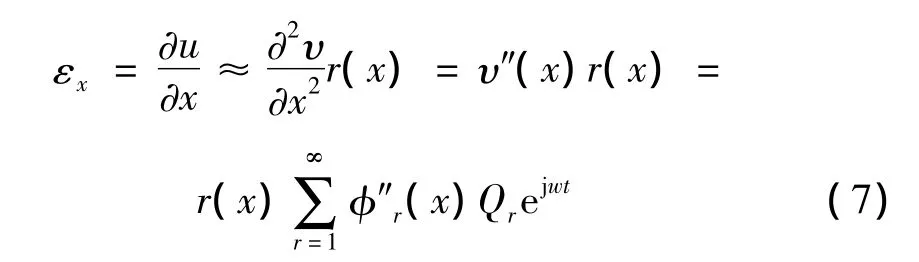
此处u为x方向的变形位移，应变模态{ψi}与曲率模态{φi}的关系根据模态的叠加性可得:

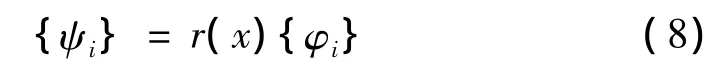
将式(8)代入式(6)中化简得:

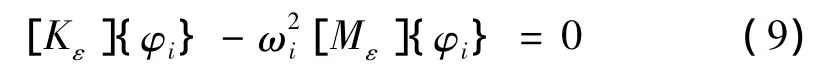
当一个n自由度无阻尼自由振动系统出现损伤时，由方程(9)得:

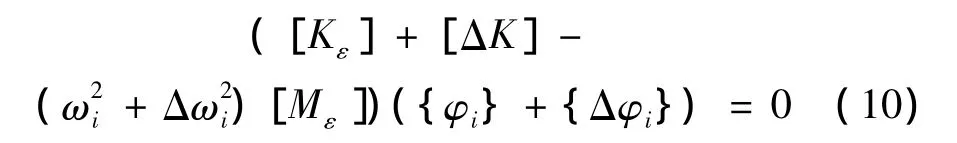
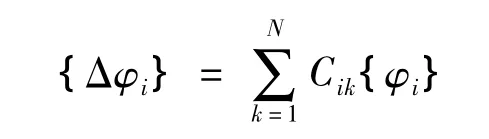
式中k为单元数;N为单元个数;Cik为损伤单元曲率改变系数。进而得出:

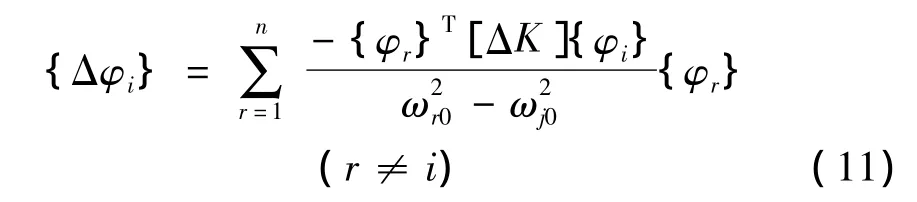
由式(6)、式(11)可推导出曲率模态变化与固有频率平方变化率的比值，即曲率、频率综合指标C为:

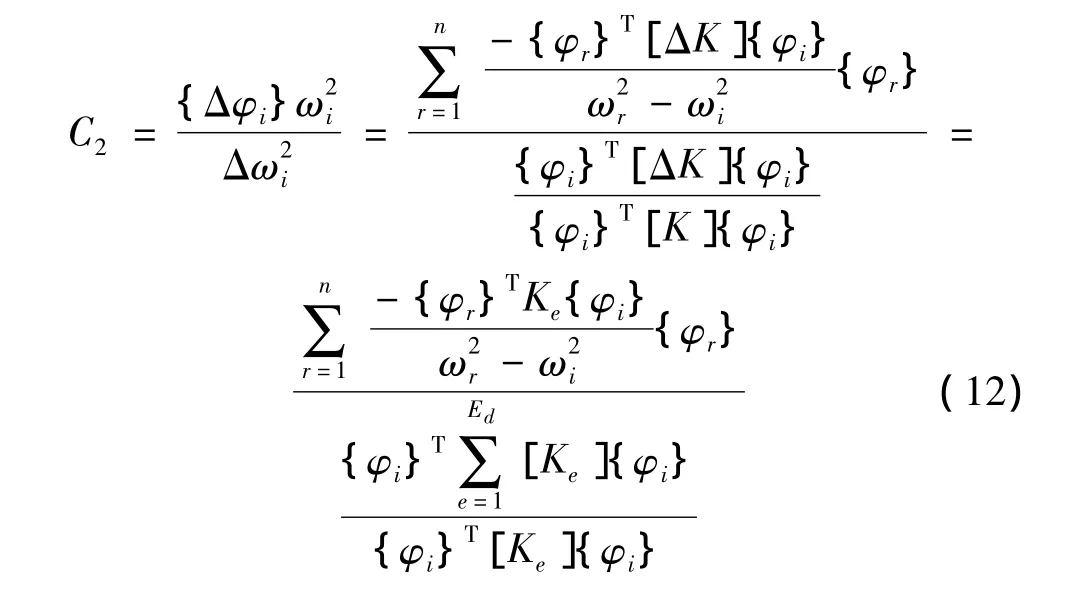
可以证明，上述曲率、频率综合指标C仅与损伤位置有关，并且是损伤位置的单调函数，因此，该指标可用于结构的损伤识别。

4 试验分析

试验模型采用两端简支的钢板矩形梁，截面为26 mm×10 mm，梁长为3.00 m，材料为Q235钢材。模型的惯性矩是 2.167E －9，弹性模量是 2.06E5 MPa，密度是7 850 kg/m2。沿梁长1/8节点处均布7个加速度传感器，同时在损伤位置处增加一个加速度传感器，共计8个加速度传感器，如图1所示。对试验模型进行表1所示的损伤工况试验。在试验过程中，通过对试验模型施加脉冲力，以模拟结构所处的自然环境，测量结构在自由振动下的加速度响应信号。

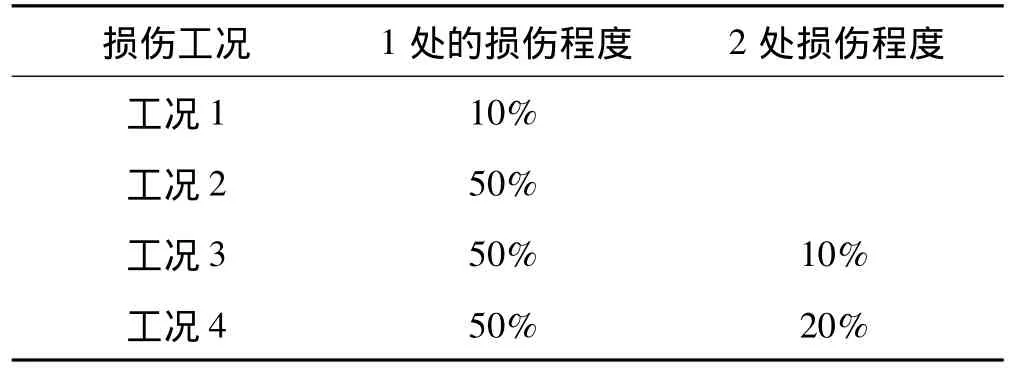
表1 梁损伤工况Tab.1 Steel beam damage case

采用随机子空间法对传感器所获的加速度传感器信号进行分析、识别。实际应用中采用稳定图方法辅助识别结构的模态参数。随机子空间方法结合稳定图识别结构模态参数过程中所需唯一人为确定参数是稳定标准的选择，在该试验分析中经反复对比筛选后，决定采用如下标准:频率稳定标准为1%，振型稳定标准为2%，阻尼稳定标准为10%。

工况4结构损伤后稳定图如图4所示。分别对各损伤工况的模态参数对比分析，不同工况下各频率识别结果如表2所示。频率表现为随着损伤程度的增加而降低。工况4损伤前后的前4阶振型如图5所示。

图4 工况4结构稳定图Fig.4 The stabilization diagram of the 4th case(?:frequency and shape stable;*:complete stable;☆:frequency stable;◇:frequency and damp stable)

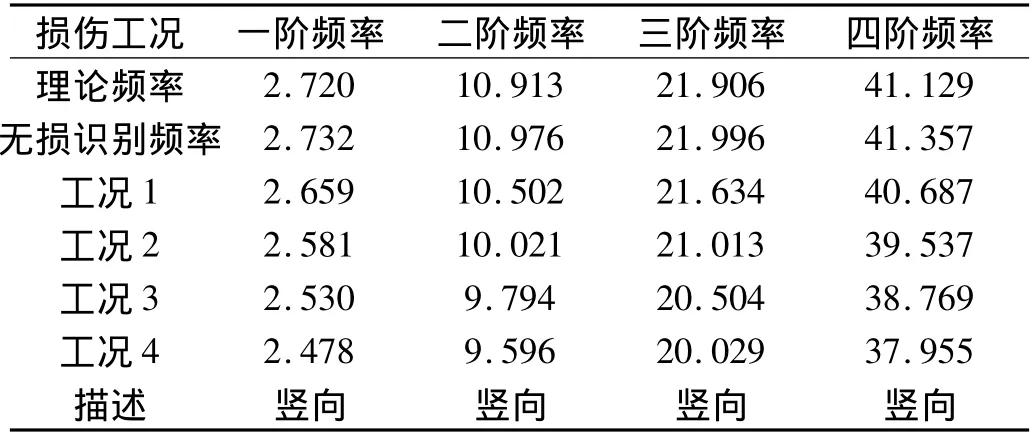
表2 不同工况下模态频率的识别结果Tab.2 The modal frequency of different case

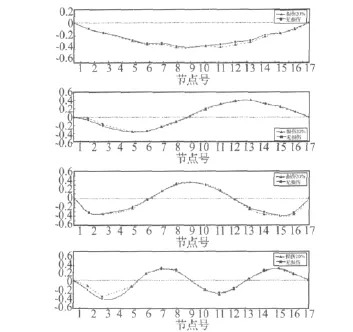
图5 工况4的前4阶振型Fig.5 The first four modal shapes of damage case 4

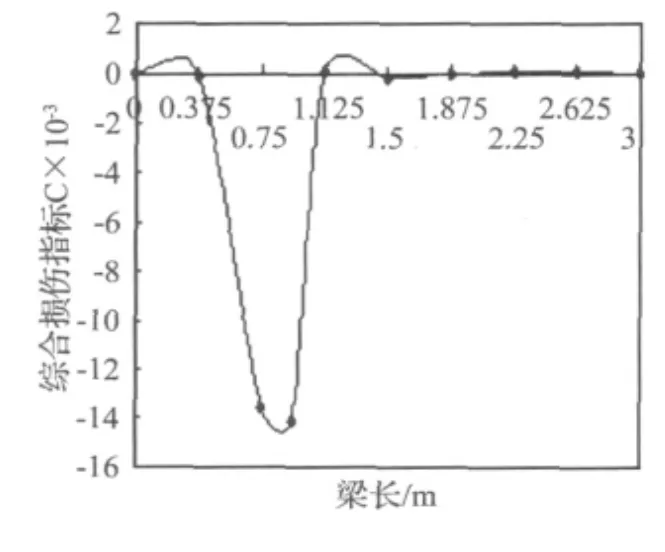
图6 工况1的识别结果Fig.6 The identification result of damage case 1

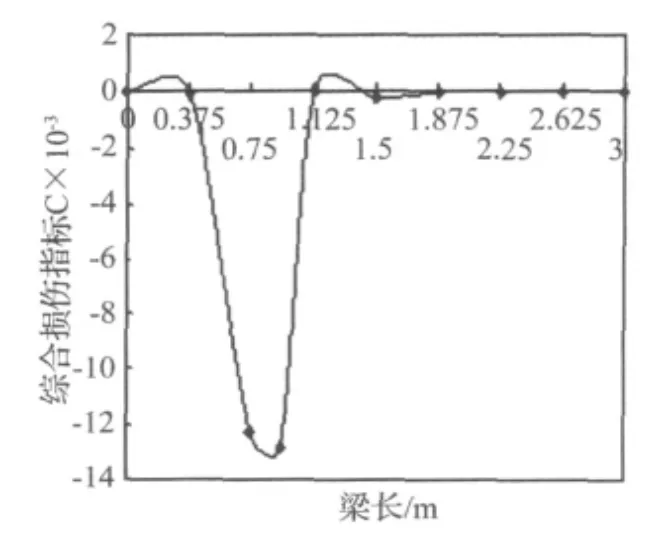
图7 工况2的识别结果Fig.7 The identification result of damage case 2

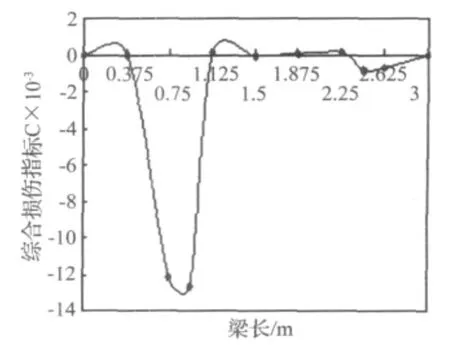
图8 工况3的识别结果Fig.8 The identification result of damage case 3

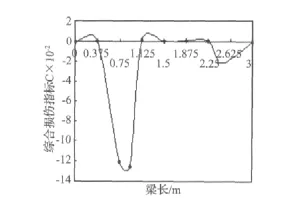
图9 工况4的识别结果Fig.9 The identification result of damage case 4

应用论文所提出的综合指标对实验室测试数据进行损伤识别。

由图6－图9可以清楚地看出:论文所提出的桥梁结构损伤识别的综合指标法能够有效地识别出各工况的损伤位置。从图中可以明显地看出单点损伤位置识别效果比较明显，多点损伤位置也能识别出，虽然图中能够显示出各不同损伤的位置的损伤大小，但数值并不太精确，只是能够定性地显示出损伤的相对大小。

5 结论

曲率模态方法对结构的局部损伤比较敏感，而频率指标具有测试简单便捷、精度高的特点，就此，本文提出了一种曲率模态变化与固有频率平方变化率比值的综合指标方法。为了使在役桥梁在损伤测试过程中不影响桥梁的正常运营，论文将随机子空间方法引入该方法中。首先采用随机子空间方法有效地从环境激励下的结构响应信号中识别出结构的模态参数;其次，采用差分法分析随机子空间方法所识别的结构振型，得出结构的曲率模态。再次，将曲率模态的变化率与频率变化率进行综合，得到综合指标C。最后，在实验室采用一简支钢梁对该方法进行了试验验证。试验结果表明:改进的在役桥梁结构损伤位置识别综合指标法结合随机子空间方法不仅比单纯的曲率模态方法识别的结果要精确得多，而且在识别过程中不会对在役的正常运营有影响。论文所提出的结构损伤位置识别方法可有效用于在役桥梁的损伤识别、桥梁结构健康监测的输入及结构状态评估中。

［1] Doebling S W，Farrar C R，Prime M B，et al.Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics:a literature review［R] .Los Alamos:Los Alamos National Laboratory，1996.

［2] Wa Hab M A，Roeck GD.Damage detection in bridges using modal curvatures:Application to a real damage scenario［J] .Journal of Sound and Vibration，1999，226(2):217－235.

［3] Pandey M B，Samman M.Damage detection from changes in curvature mode shapes［J] .Journal of Sound and Vibration，1991，145(2):321－332.

［4] 常 军，张启伟，孙利民.一种分段平稳随机信号的参数识别方法［J] .振动与冲击，2007，26(6):17－20.

［5] Van Overschee P，De Moor B.Subspace identification for linear systems:theory-implementation-applications［M] .Kluwer Academic Publishers， Dordrecht， The Netherlands，1996.

［6] Peeters B，De Roeck G.Reference-based stochastic subspace identification for output-only modal analysis［J] .Mechanical Systems and Signal Processing，1999，13(6):855－878.

［7] Peeters B，De Roeck G.Reference-based stochastic subspace identification in civil engineering［J] .Inverse Problems in Engineering，1999，100:128.

［8] Poly A B.Reference version of subspace algorithms for output only structural identification ［C] //18th MAC，2000，620－624.

［9] 常 军，张启伟，孙利民.稳定图方法在随机子空间识别模态参数中的应用［J] .工程力学，2007，24(2):39 －44.

［10] 常 军，张启伟，孙利民.随机子空间方法产生虚假模态原因分析［J] .工程力学，2007，26(11):57 －62.

［11] 常 军.基于曲率模态的钢筋混凝土梁多点损伤位置识别［J] .建筑科学与工程学报，2006，23(4):24－27.

［12] 王成强，陈怀海，姜双燕，等.基于转角模态曲率的损伤识别研究［J] .海军航空工程学院学报，2009，24(3):24－27.

［13] 赵 俊，程良彦，马宏伟.基于曲率模态的拱板结构损伤识别［J] .暨南大学学报(自然科学版)，2009，29(5):470－476.

［14] 张育智，李 乔，单德山.SOFM网络在结构损伤位置识别中的应用［J] .振动与冲击，2007，26(2):160 －163，170.