复杂形体超高钢结构电视塔抗震性能分析研究

李春祥， 汪英俊， 钟秋云， 秦季标

(1.上海大学 土木工程系，上海 200072;2.上海浦桥工程建设监理有限公司，上海 200090)

1 工程简介

近年来，随着广播、电视、通讯等事业的迅猛发展，我国相继建成了一系列体型新颖的大型多功能现代超高电视塔。这些现代超高电视塔除了提供广播电视发射的主要功能，同时还具备了旅游观光、休闲娱乐等功能，实际上是一个城市的标志性建筑和地区的象征。例如，位于上海陆家嘴商业区的高468 m东方明珠电视塔［1]和高610 m 广州新电视塔［2]。从结构形式看，现代超高电视塔融入了高层建筑的特点，往往在顶部设有楼层，是一种综合性的超高高层－高耸建筑。超高高层－高耸建筑由于质量和刚度存在突变，高宽比较大，平面与竖向不规则性等特性使其在风和地震作用下的动力响应很强烈。现代超高电视塔设计过程中追求个性化的设计思想，体系日趋多样性、建筑平面布置与竖向体型也越来越复杂，因而受力状况表现出复杂性和不确定性。这些重大复杂形体建筑给结构抗震抗风分析与抗震抗风设计带来了许多新的问题。

拟建宁夏电视塔(NXTVT)(高320 m)造型独特、建筑形体复杂。NXTVT不仅代表宁夏，而且还表征着技术、艺术、创新、人民、环境、个性 (Technology、Art、Innovation、People、Environment、Identity，TAIOEI)。NXTVT体型呈现底部小、上部大、中部略呈细腰形且设计有三段楼层共计28层的花瓶状形体，其立面示意图如图1所示。结构上部最大外围尺寸为118.4m，中间最小外围尺寸为33.4m，柱脚处外围尺寸为46.5 m。结构方案I:钢框架－支撑内筒体系。外框架共设有6根弧形外柱，其中每2根由巨型桁架连接成一组，在71 m、148 m、222 m高分别设置6根拉索连接内筒和6根外柱。NXTVT楼层段位置:第一段楼层(下部)位于20 m至32 m处，共4层;第二段楼层(中部)位于79 m至107 m处，共8层;第三段楼层(上部)位于156 m至216 m处，共16层。第一段楼层和第二段楼层间的透空区高为47m，第二段楼层和第三段楼层间的透空区49 m高。在有楼层处，外柱与内筒通过钢梁、钢桁架相连，楼板采用压型钢板组合楼板;而在透空区，外柱与内筒无连接，仅靠外柱和内筒的各自自身刚度形成结构抗侧刚度。

根据结构的平面、立面布置及结构体系，该结构具有以下几个特征:① 结构高宽比H/B=216 m/46.5 m=4.65，满足我国《建筑抗震设计规范》8.1.2 条关于钢结构民用房屋最大高宽比的要求;② NXTVT建筑平面形状呈Y型，如图2所标注，凹进尺寸与该方向投影总尺寸之比 =27.98/73.42=0.381 ＞0.3，由《建筑抗震设计规范》3.4.2条“结构平面凹进的一侧尺寸，大于相应投影方向总尺寸的30%”可以判定该结构体系属于平面不规则类型中的凹凸不规则;③ NXTVT第三段楼层的内柱落在转换桁架(156 m高度)上，竖向抗侧力构件的内力由水平转换构件向下传递，出现高位转换层。由《建筑抗震设计规范》3.4.2条可以判定该结构体系属于竖向不规则中的竖向抗侧力构件不连续;同时，该结构两段透空区会引起结构侧向刚度的明显变化。④ NXTVT立面从大－小－大尺寸的变化，且上部楼层数量多、质量大，质量多集中结构上部，对抗震不利。从概念分析知，此建筑形体和楼层布置在地震作用下的倾覆力矩大于总质量、高度相等但质量均匀分布的建筑形式［3]。

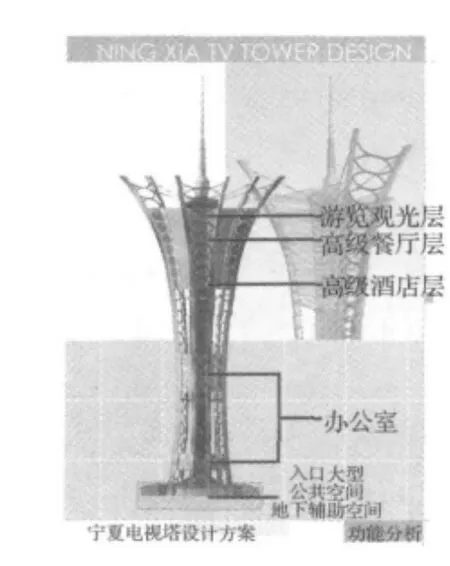
图1 NXTVT立面图Fig.1 Elevation view of NXTVT

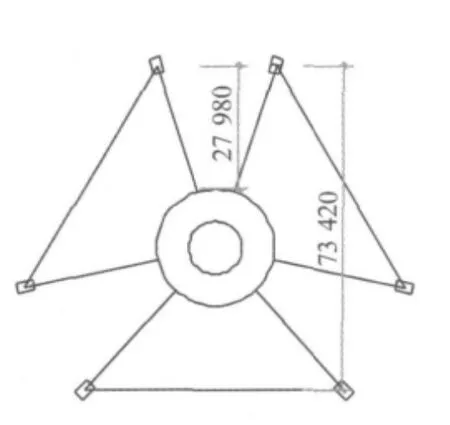
图2 NXTVT有楼层处典型平面图Fig.2 Typical plan view of NXTVT

图3 NXTVT的ANSYS三维模型图Fig.3 ANSYS model of NXTVT

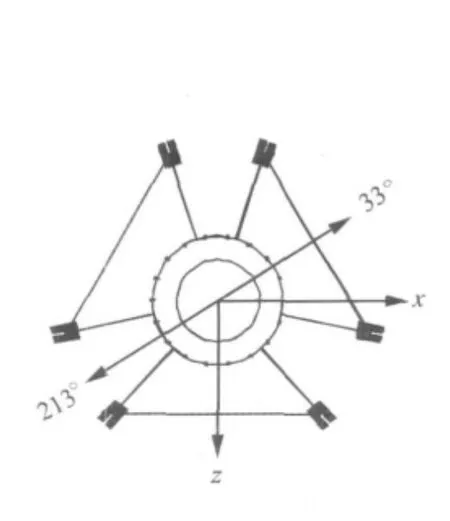
图4 抗震分析坐标系Fig.4 Coordinate system for seismic analysis

当前，国内结构计算软件主要分为专业软件和通用软件两大类，专业软件对竖向刚度分布均匀的结构计算结果良好。但是NXTVT形体复杂，专业软件的计算假设多，有一定误差。通用软件ANSYS和SAP2000等是世界上颇有影响的大型通用有限元分析软件，可完成大型复杂几何结构的静力分析、模态分析、瞬态动力分析和谱分析等。例如，文献［4，5] 基于通用软件ANSYS和SAP2000分别对331 m的武汉国际证券大厦、388 m的河南省广播电视塔进行了抗震分析。最近，文献［6] 进行了大型超高钢结构电视塔模拟地震振动台试验研究。考虑到NXTVT的楼层多达28层，功能定位非常倾向高层建筑，且结构形式新颖独特，国内外罕见，因此，本文使用通用软件ANSYS对NXTVT进行动力特性和抗震性能分析。同时，就结构固有频率，将ANSYS计算结果与SAP2000计算结果进行比较。

2 建立NXTVT的ANSYS分析模型

NXTVT钢材选用 Q345钢，楼层混凝土标号为C40。NXTVT抗震性能分析时采用的重力荷载代表值取为1.0倍恒载+0.5倍活载，其中，恒载包括结构构件自重以及非结构构件质量等。经ANSYS计算，电视塔的总重力荷载代表值为460 240 KN。在ANSYS有限元模型中，梁柱采用Beam188单元;分析模型考虑楼面板弹性，因而采用shell63单元;质量块采用Mass21单元;拉索采用Link10单元;桅杆梁柱采用Pipe16单元。整个结构有限元模型共计52 800个单元，63 350个节点，三维ANSYS有限元分析模型如图3所示。塔身有楼层处典型平面图如图4所示;抗震分析时，x和z坐标系如图4所示(注:本文Y轴为高度方向)。

3 NXTVT动力特性分析

3.1 结构的周期和振型

分析结构动力特性是了解结构的重要途径，同时也是振型分解反应谱法的基础。因结构中设有预应力拉索，所以在ANSYS中采用分块Lanczos预应力模态分析方法。鉴于 NXTVT的复杂性，本文同时使用SAP2000建立了三维有限元模型，采用特征值向量法，以非线性静力分析终态作为模态分析的初始状态进行动力特性分析。ANSYS和SAP2000分析结果的前30阶频率列于表1。

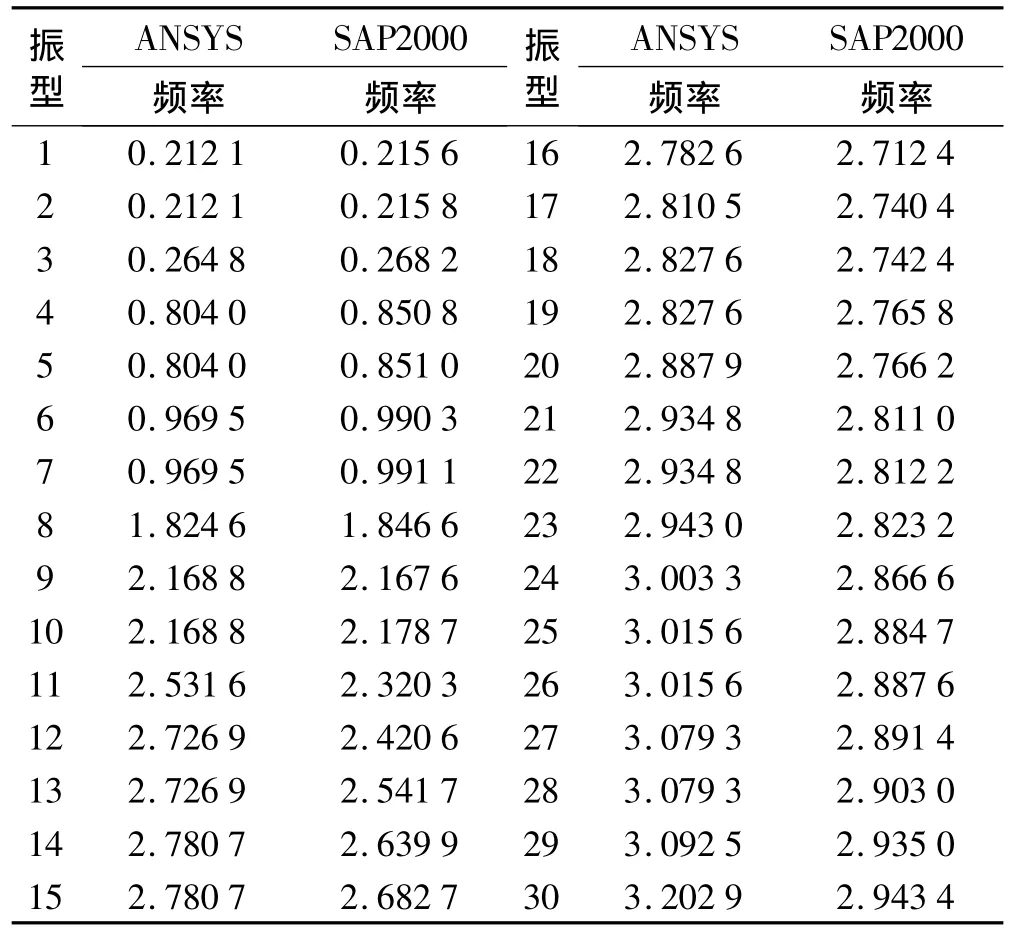
表1 结构前30阶自振频率Tab.1 First thirty modal frequencies of NXTVT

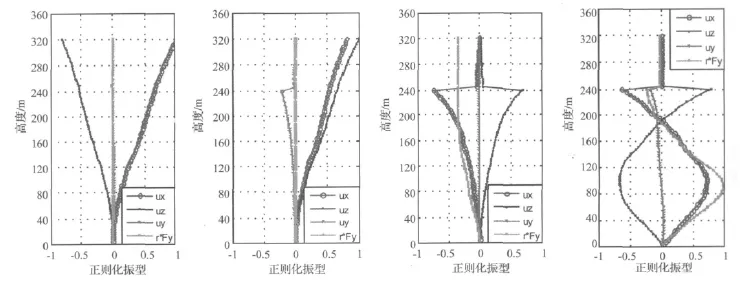
图5 耦合3D振型Fig.5 Coupled 3D mode shapes

表2 结构的第1－3和8阶振型俯视图Tab.2 vertical views of the first，second，third，and eighth mode shapes of NXTVT

由表1知:ANSYS和SAP2000计算结果非常接近，SAP2000计算得到的第一振型频率为0.215 6 Hz，与ANSYS计算结果相差不到2%。由图5和表2知:第1、2阶为结构整体沿水平方向第一横向振动;第3阶为整体扭转并伴随一定的水平振动;第8阶为3组巨型外柱的扭转振动。

由表1－表2和图5可得出如下主要结论:

(1)结构的基频较低，第一振型频率为0.212 1 Hz，周期4.715 2 s，反映结构的整体刚度较柔。

(2)结构以扭转为主的第一自振周期Tt与以平动为主的第一自振周期T1之比值为3.776 6/4.715 2=0.800 9，扭平比小于 0.85［7]，满足规范要求。

(3)结构沿x方向平动与z向平动周期相等，表明结构在x和z方向的抗侧刚度相当。

(4)结构振型以平动振型为主，第一扭转振型出现在第3阶。

(5)表1的数据显示，该结构高阶振型的频率密集，相邻各阶频率相差不超过0.2 Hz，因而在对该结构进行抗震设计时，高阶振型的影响不可忽视。最后，值得指出的是，本文中的Y向指的是结构高度方向，Y方向振型即竖向振型，主要出现在10阶以后，与高层建筑结构的振型主要为水平振型的概念判断是相符的。

3.2 振型参与系数

计算得到结构在各个方向上的振型参与系数如图6所示。由图6可知，X、Z方向上均为低阶振型起控制作用，而Y方向上则第11、16、20、40阶振型起控制作用。

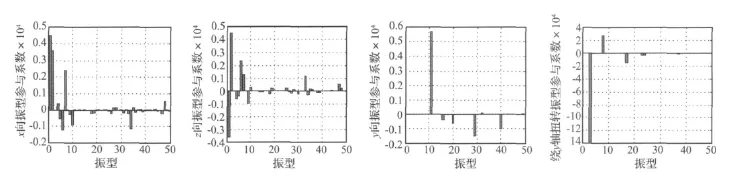
图 6 X、Y、Z、RotY 方向振型参与系数Fig.6 Participation factors of vibration modes

3.3 合理振型数目

为满足振型分解反应谱法计算精度的需要，对振型求解提出了水平向振型质量参与系数之和超过0.9的要求。图7的横坐标为振型，纵坐标为振型参与质量/总质量。经试算，可以得到当参与质量达到90%时，需要的振型分别为16阶(X方向)、16阶(Z方向)。考虑到该结构的竖向质量分布不均匀，在使用振型分解反应谱法时，截取前50阶进行计算。从图7可以看出，在取50阶振型计算时，沿Y向的振型参与质量系数之和为78%，接近80%。可以判断取50阶计算基本满足考虑竖向振型的要求。为了进一步了解该电视塔竖向振型参与质量系数与振型阶数的关系，在动力特性分析阶段分别提取了100阶和300阶振型计算的结果，深入研究了竖向振型参与质量系数与扩展模态阶数的关系，如图8所示。从该图可以看出，在阶数增加至300阶时，竖向振型参与质量系数之和与50阶相比并无太大变化，仅从77.9%提高到83.9%。在考虑计算效率的前提下，在使用振型分解反应谱法时截取前50阶进行计算足以充分考虑竖向地震作用。

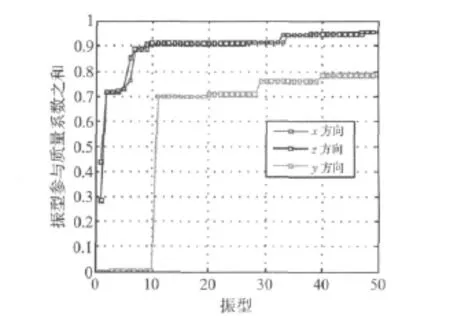
图7 振型参与质量系数Fig.7 Modal participating mass ratio

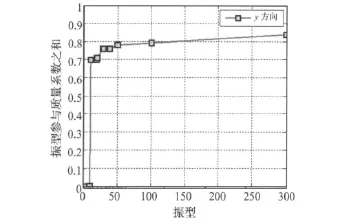
图8 Y向振型参与质量系数Fig.8 Y-direction modal participating mass ratio

4 结构的振型分解反应谱法分析

NXTVT位于宁夏银川市市区，抗震设防烈度为8度，50年超越概率为10%的设计基本地震水平加速度峰值为0.2 g，设计分组为第一组;场地类别属Ⅱ类，为中软场地土;建筑抗震设防类别:特殊设防类，简称甲类。在结构方案验证阶段，地震作用计算时抗震设防烈度按9度考虑。由该电视塔的场地类别和抗震设计分组，根据《建筑抗震设计规范》可查到该结构的特征周期为0.35 s;由抗震设防烈度可查得多遇地震水平地震影响系数最大值为0.32。多遇地震作用下结构的抗震性能分析时，其阻尼比取为0.02，根据文献［8] 中5.1.5 条可计算得:γ =0.95，η1=0.024，η2=1.32，其中γ、η1、η2分别为反应谱曲线下降段的衰减指数、下降斜率调整系数、阻尼调整系数。

4.1 结构基底剪力和关键点处位移

本文分别进行了单向、双向和三向振型分解反应谱法分析，振型组合采用CQC方法，方向组合采用SRSS遇合法则。单向、双向和三向振型分解反应谱法得到的结构基底剪力与剪力系数列于表3。

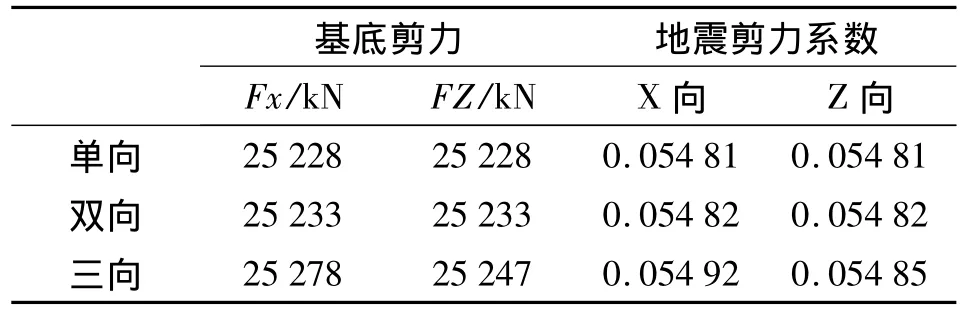
表3 使用振型分解反应谱法得到的结构基底剪力与剪力系数Tab.3 Base shears and shear coefficients obtained using the response spectrum method

由表3知，结构最小基底剪力系数为0.054 81，大于《建筑抗震设计规范》规定的0.045，基底剪力系数值在正常范围内，结构设计合理。在单向、双向和三向地震作用下，结构在x和z方向上的底部剪力数值相差都较小，表明结构沿两个水平主轴方向的抗侧刚度大致相同;在选取了足够多考虑竖向地震作用的模态阶数后，双向和三向地震作用下结构基底剪力相差不到1%，说明竖向地震作用对结构基底剪力的贡献不明显。

4.2 结构水平位移和层间位移角

本文中，水平方向取值比例是根据文献［8] 中5.2.3条对双向水平地震作用的规定，竖向地震作用组合则是参照文献［8] 在动力时程分析时取0.65的建议。具体计算时，以x100、z100、y100分别表示沿 X、Z、Y方向的单向谱计算，x100 z085表示按文献［8] 中式5.2.3 －7、x085 z100 表示按文献［8] 中式 5.2.3 －8 双向谱计算，x100 z085 y065、x085 z100 y065则在分别表示的基础上组合了0.65倍的竖向地震，并称100所在方向为主组合方向。

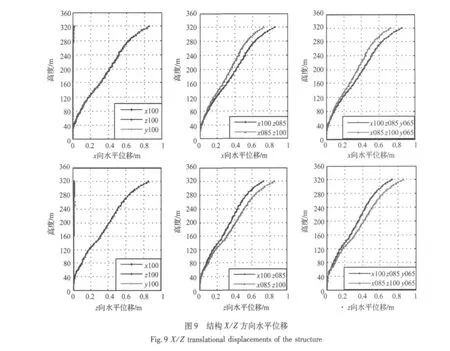
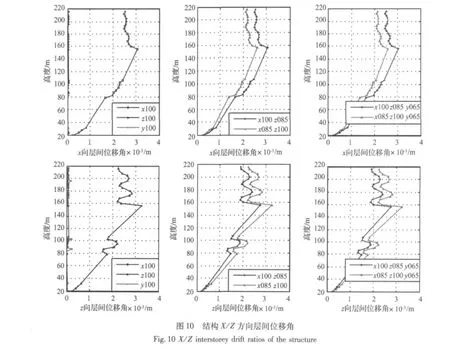
单向、双向、三向谱分析得到的结构水平位移和层间位移角分别如图9－图10所示。由图9－图10可得出如下主要结论:

(1)沿X和Z方向的水平位移响应几乎相同，表明沿X和Y方向的抗侧刚度非常接近。

(2)结构变形以弯曲变形为主，位移随高度增加持续增大。

(3)在有楼层处，结构刚度较大，层间位移角相对较小，例如第一段楼层处(高度20 m－32 m)，第二段楼层处(高度79 m－107 m)，第三段楼层处(高度156 m －216 m)。

(4)在无楼层处，结构抗侧刚度较小，层间位移角随高度增加持续增大，例如第一段透空区(高度32 m－79 m)，第二段透空区(高度107 m－156 m)。

(5)在有楼层段与无楼层段交接处，结构抗侧刚度突变，相应地体现在层间位移角变化上，尤其是在156 m位置处，为结构的薄弱区域。

(6)在9度地震作用下，结构最大层间位移角为1/308，满足我国抗震规范的要求。

5 弹性动力时程补充验算

5.1 基底剪力

根据NXTVT场地特征，本文选用El－Centro东西波［9](加速度峰值 2.099 2 m/s2)，Hollywood storage 南北波和1组人工波进行动力弹性时程分析。三维弹性动力时程分析时，X、Y、Z方向三个方向加速度峰值比即 x100 y085 z065 是取为 1∶0.85∶0.65，x085 y100 z065是取为0.85∶1∶0.65，以下称1.0 比例分量所在的水平方向为输入主方向。根据《建筑抗震设计规范》(GB 50011－2001)，地震作用持续时间不小于结构基本周期(T1=4.715 2 s)的5倍－10倍，因此本文取为30 s。弹性动力时程补充验算阶段，地震加速度时程输入的最大值为140 cm/s2，三条地震波均按照这一最大值进行调幅处理。弹性动力时程分析采用Newmark-β积分算法，其中积分参数 α =0.252 5，δ=0.505。考虑到结构中存在拉索，在进行多遇地震弹性动力时程分析时应考虑结构的几何非线性影响。表4给出了动力时程分析与振型分解反应谱分析得到的基底剪力，表中，RSM表示反应谱法结果，DTM表示动力时程法结果，ADTM表示动力时程法结果的平均值。

由表4可看出，在多遇地震作用下，结构动力时程分析的结果与反应谱分析的结果基本一致;而且每条地震时程曲线所计算出的结构底部剪力不小于振型分解反应谱法计算结果的65%;3条地震时程曲线计算所得的结构底部剪力平均值不小于振型分解反应谱法计算结果的80%。因此，弹性动力时程补充验算结果符合《建筑抗震设计规范》对于时程分析的计算要求。同时，取前述3条地震波计算结果的平均值与振型分解反应谱法计算结果的较大值来进行地震作用的设计验算。从表4可看出:结构动力时程分析结果的平均值大于振型分解反应谱法，为抗震计算的控制性分析方法。

5.2 水平位移和层间位移角

图11给出了结构在一维、二维、三维输入下楼层水平位移响应包络图，而图12给出了相应的楼层层间位移角。从图11可看出，采用的地震加速度时程曲线，虽然其加速度峰值相同，但每条地震波均有自己的频谱特性，不同地震波计算出的结构地震响应存在较大的差别，在不同的楼层段，最大值也不一样。因此，地震波的选取以及选取的数量都应予以重视，建议取多条地震波计算结果的平均值。在桅杆的顶部，在Holleywood Storage波时结构的响应最大，桅杆顶端最大水平位移为1.15m，但小于结构总高度1/100的控制值［10]。3条地震波作用下结构变形的共同特点是，桅杆部位的水平位移都放大，鞭稍效应明显。结构的层间位移角最大值均出现在156m高度处，此处为无楼层到上部楼层的交界面，结构刚度突变，为结构的薄弱部位，因此该位置需要采取构造措施进行加强处理。人工波作用下结构的层间位移角最大，其最大值为1/389，小于1/300，满足我国相关规范要求。由图11和12可得出与反应谱法相同的结论，即该结构沿X和Z两个水平方向的抗侧刚度大致相当。结合图9与图11可以看出，结构的位移响应:中部楼层段、上部楼层段以及桅杆中下段反应谱法大于动力时程分析的平均值，下部楼层段及桅杆顶部段则反应谱法结果小于时程分析平均值，尤其是桅杆顶部的鞭稍效应，可见动力时程分析能更清晰地反应结构桅杆顶部的鞭稍效应。因此，像电视塔结构这类结构进行地震作用计算时，应综合采用反应谱和弹性动力时程两种方法的分析结果。

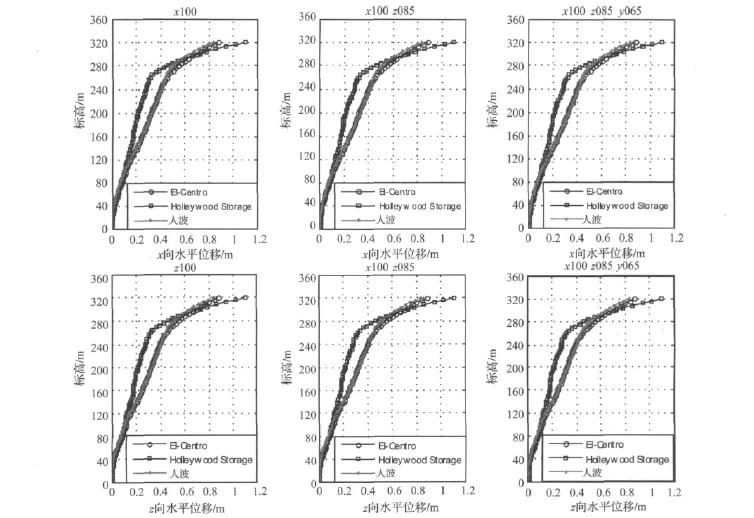
图11 结构X/Z方向水平位移包络图Fig.11 Envelope of X/Z translational displacements of the structure

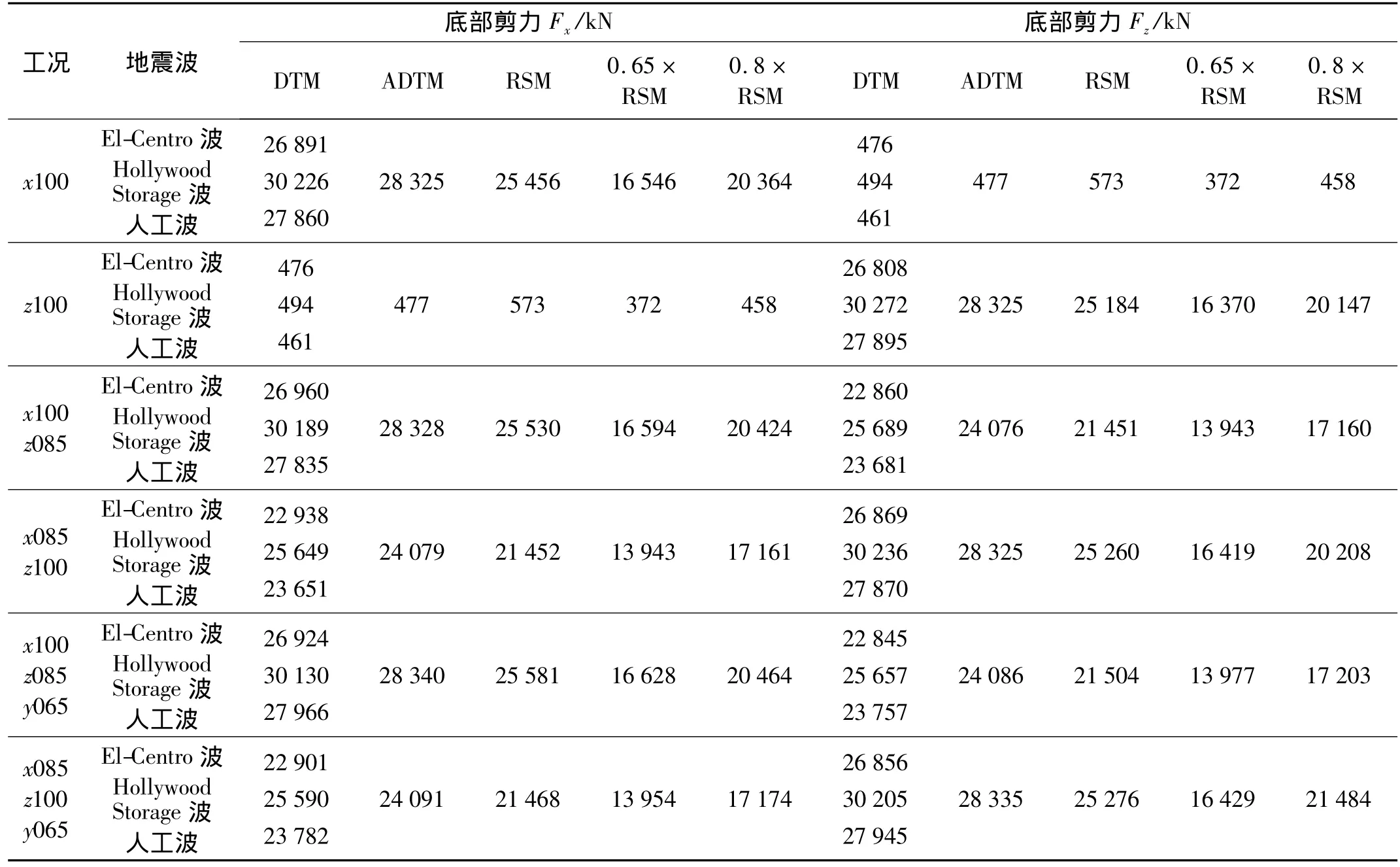
表4 动力时程法(DTM)和反应谱法(RSM)得到的基底剪力Tab.4 Base shear force using dynamic time-history analysis(DTM)and response spectral analysis(RSM)

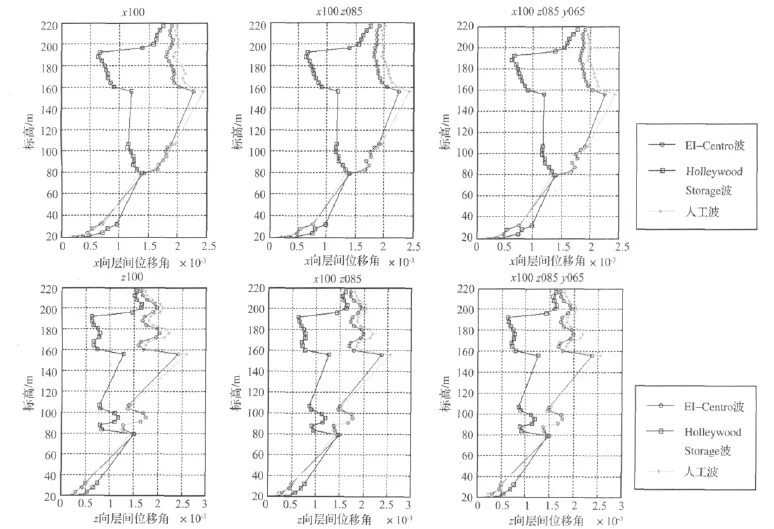
图12 楼层X/Z向层间位移角包络图Fig.12 Envelope of X/Z inter－ story drift ratios of the structure

现在，分别选取三个楼层段最上面一层，即标高为32 m、107 m、216 m的3个楼层，观察它们在不同频率成分地震波作用下，结构不同高度楼层的水平位移、速度、加速度响应时程曲线，如图13、图14、图15所示。

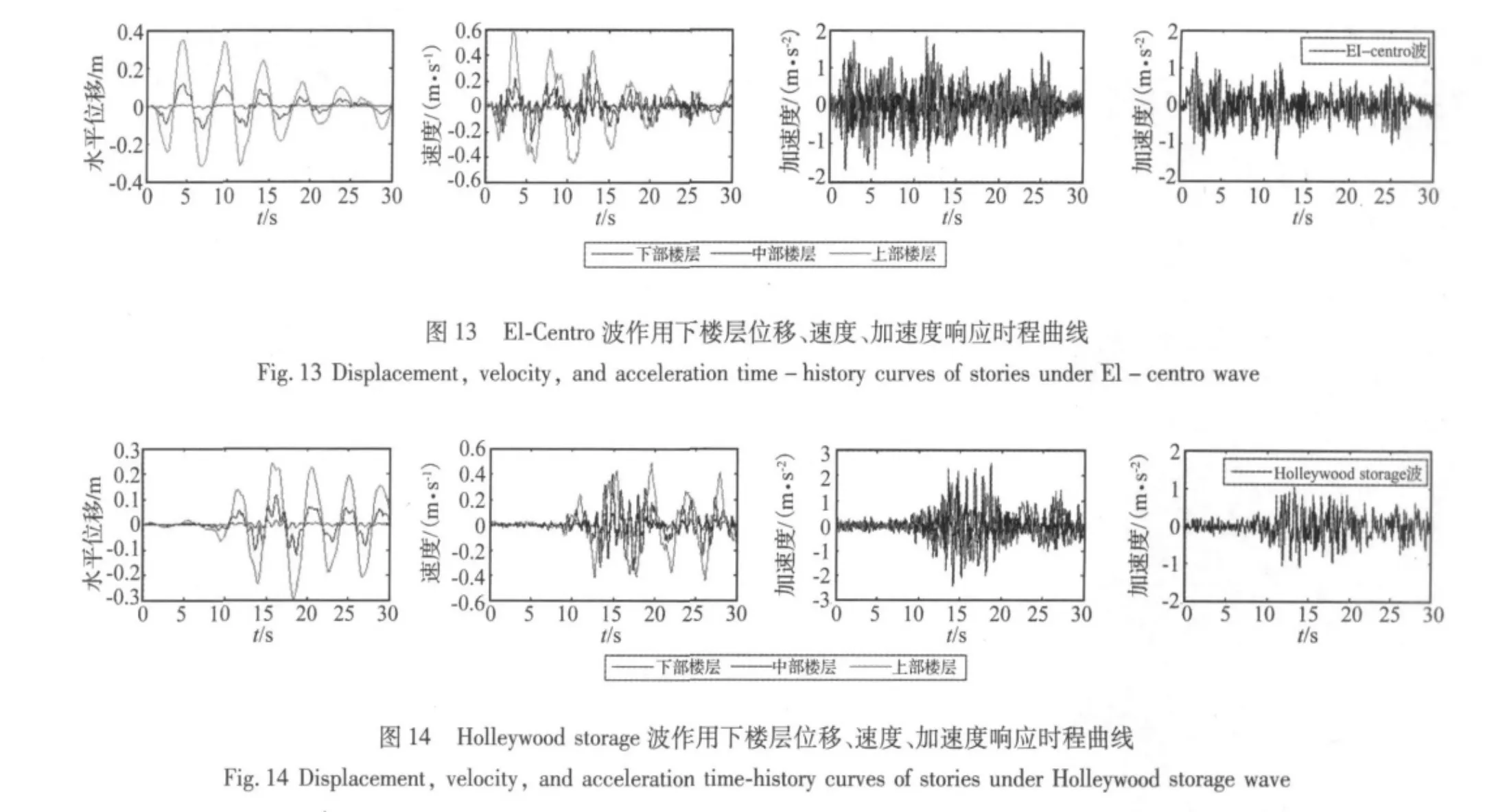
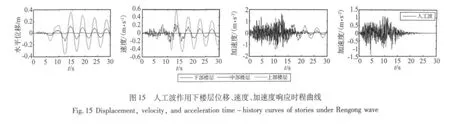
图13－图15表明，3条地震波分别作用下，三段楼层响应的相似之处为:三段楼层水平位移幅值的变化与地震波输入幅值变化基本保持一致;速度时程曲线的变化与位移基本一致，但下、中、上楼层的速度依次增大，说明楼层位置越高速度响应的放大作用越大;加速度响应时程曲线则显示不同位置楼层的加速度值达到峰值的时刻也不相同。3条地震波分别作用下，三段楼层响应的不同之处:El－centro波作用下加速度达到峰值中部楼层最早、下部次之、上部最后，加速度峰值出现在上部楼层;Holleywood storage波作用下加速度达到峰值上部楼层最早、下部次之、中部最后，加速度峰值出现在中部楼层;人工波作用下，加速度达到峰值下部楼层最早、中部次之、上部最后，加速度峰值出现在中部楼层。均匀的结构加速度峰值基本出现在顶层，NXTVT两段透空区的存在使结构加速度值沿高度的变化变得复杂，两条波作用下加速度峰值出现在中部楼层，说明略呈细腰形的中部楼层是结构的薄弱部位，设计时应引起注意。

为分析地震输入维数对结构地震响应的影响，以El－centro波作用下上部楼层响应为例(如图16所示)，对不同维数地震波输入下结构地震响应进行比较。以X方向为主输入方向时，X方向的水平位移在x100、x100 z085输入时基本一致;而Z向水平位移则在x100输入时非常小，与x100 z085输入时相比基本可以忽略不计;以Z方向为主输入方向时，X向水平位移在z100输入时非常小，与x085 z100输入时相比基本可以忽略不计，而Z方向的水平位移在z100、x085 z100输入时基本一致。可见，单向水平地震作用能反映在输入方向的效应，而结构在非输入方向的效应基本无法体现。因此，双向水平地震作用分析更能真实地反映结构的地震反应。

同时，由图可以看出，在x100 z085、x100 z085 y065输入时，无论X、Z方向的位移都基本保持一致;在x085 z100、x085 z100 y065输入时，在X、Z方向的位移也几乎相等。可以总结出，双向水平地震输入下结构X、Z向位移与三维地震输入下结构X、Z向位移几乎相等(相差在1%以内)，再次表明竖向地震对结构水平位移影响较小，与反应谱法得到的结论一致。

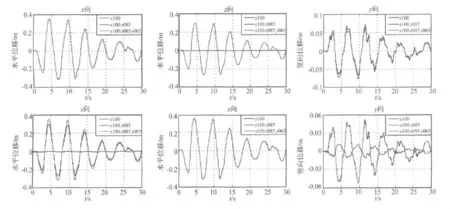
图16 不同维数地震作用下上部楼层的水平位移Fig.16 Displacements of upper story under different dimension earthquake excitations

6 弹塑性动力时程分析

弹塑性动力时程分析中，钢材的弹塑性本构关系采用经典双线性随动强化模型(如图17所示)，采用弹性斜率和塑性斜率的双线性曲线来表示应力应变关系，初始弹性模量2.06×105N/mm2，强化模量取初始弹性模量的1%。屈服准则采用Von mises屈服准则，并考虑随动强化体现鲍辛格效应。在分析中，在弹塑性分析时楼面板、拉索等仍按弹性考虑。结构的阻尼比取为0.05，并考虑“P－Δ”效应和大变形效应。

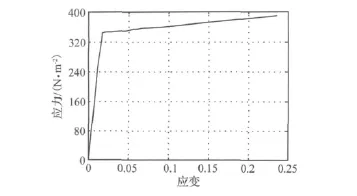
图17 钢材应力－应变曲线Fig.17 The relationship of stress-strain of steel

仍然选用前述的三条地震波曲线并定义时程函数，分别按照8 度(0.2 g)、8 度(0.3 g)、9 度罕遇地震最大加速度 400 cm/s2、510 cm/s2、620 cm/s2进行峰值调整，并按照X:Z:Y=1:0.85:0.65的比例同时施加三个方向的地震加速度。本文采用稳定性较好的Newmark-β算法，且最大计算时间步长取0.002 s，以保证非线性动力分析的稳定性、收敛性和精确性。根据《建筑抗震设计规范》第5.5.5条规定:结构薄弱层的弹塑性层间位移角限制对于高层钢结构为1/50。

6.1 水平位移和层间位移角

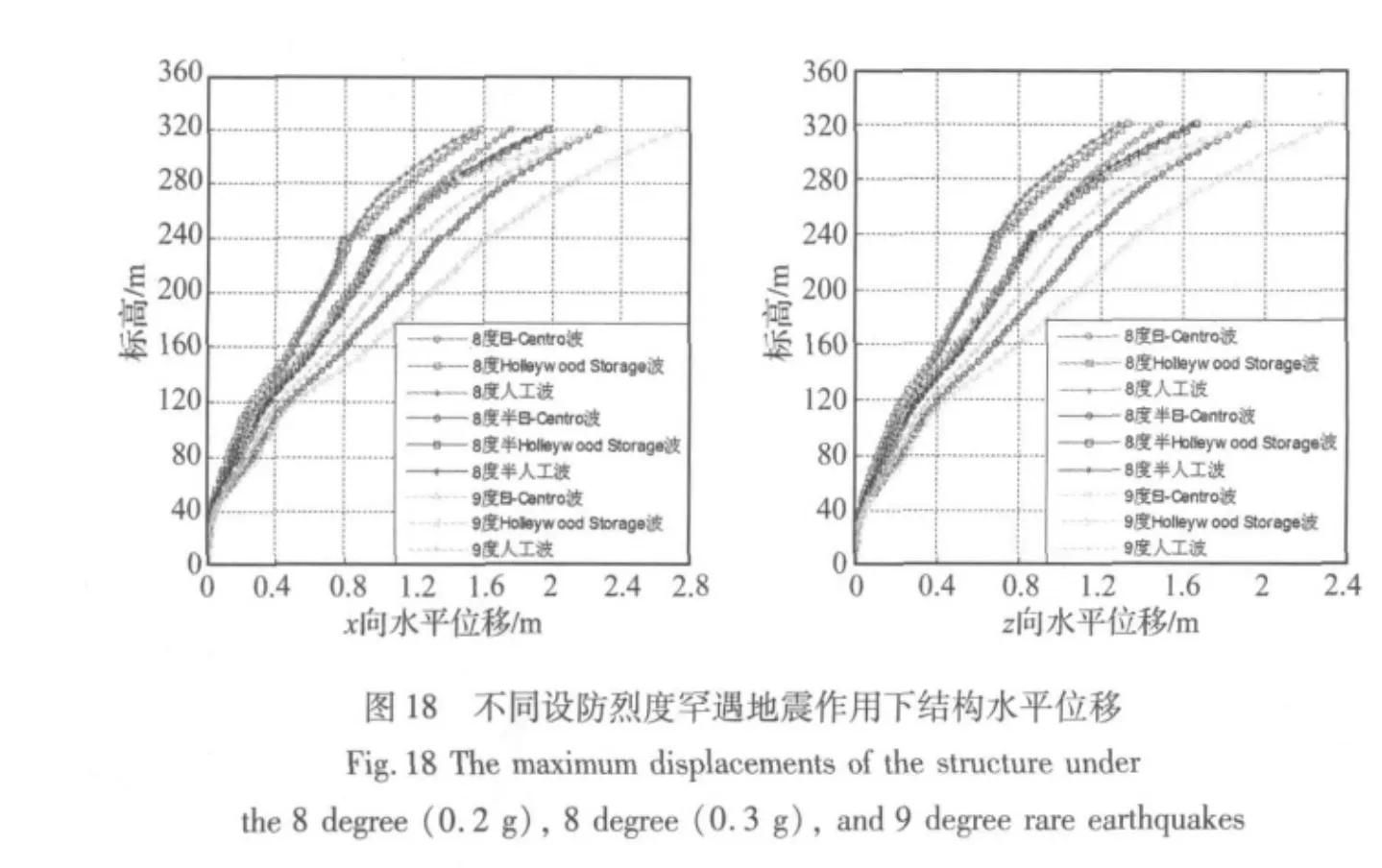
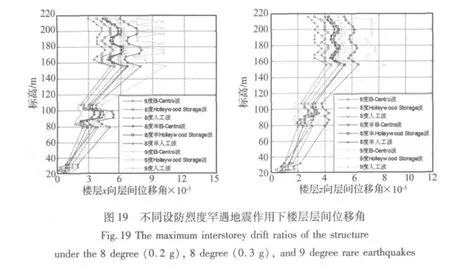
取标高32 m、107 m、216 m的3个楼层外柱处的节点以及桅杆顶点为结构关键节点，表5为不同设防烈度罕遇地震作用下关键节点处的最大位移及最大层间位移角。图18为不同设防烈度罕遇地震作用下x100 z085 y065输入时结构X向、Z向各质点沿高度的水平位移曲线，而图19为相应的楼层层间位移角。结合表5和图18可以看出，在8度(0.2 g)罕遇地震作用下，桅杆顶部水平位移在El－Centro波作用下最大，X向最大水平位移为1.75 m，而弹性地震作用下桅杆点水平位移最大值为1.15 m，可见8度(0.2 g)罕遇地震作用下的最大水平位移比弹性地震作用下大了50%;8度(0.3 g)罕遇地震作用下，X向最大水平位移为2.27 m，可见8度(0.3 g)罕遇地震作用下的最大水平位移比8度(0.2 g)罕遇大了约30%;9度罕遇地震作用下，X向最大水平位移为2.73 m，可见9度罕遇地震作用下的最大水平位移比8度(0.3 g)罕遇大了约20%。

由图19可以看出，无论是在8度(0.2 g)、8度度(0.3 g)还是9度设防烈度下，El-centro波作用下结构层间位移角明显大于另两条波下，而最大值均出现在156 m高。在8度(0.2 g)罕遇地震作用下结构的最大层间位移角为1/164，8度(0.3 g)楼层弹塑性层间位移角最大值为1/127，9度时楼层弹塑性层间位移角最大值为1/98，可见结构在9度罕遇到地震作用下层间位移角仍然小于《建筑抗震设计规范》(GB50011－2002)规定的1/50限值，满足规范要求。

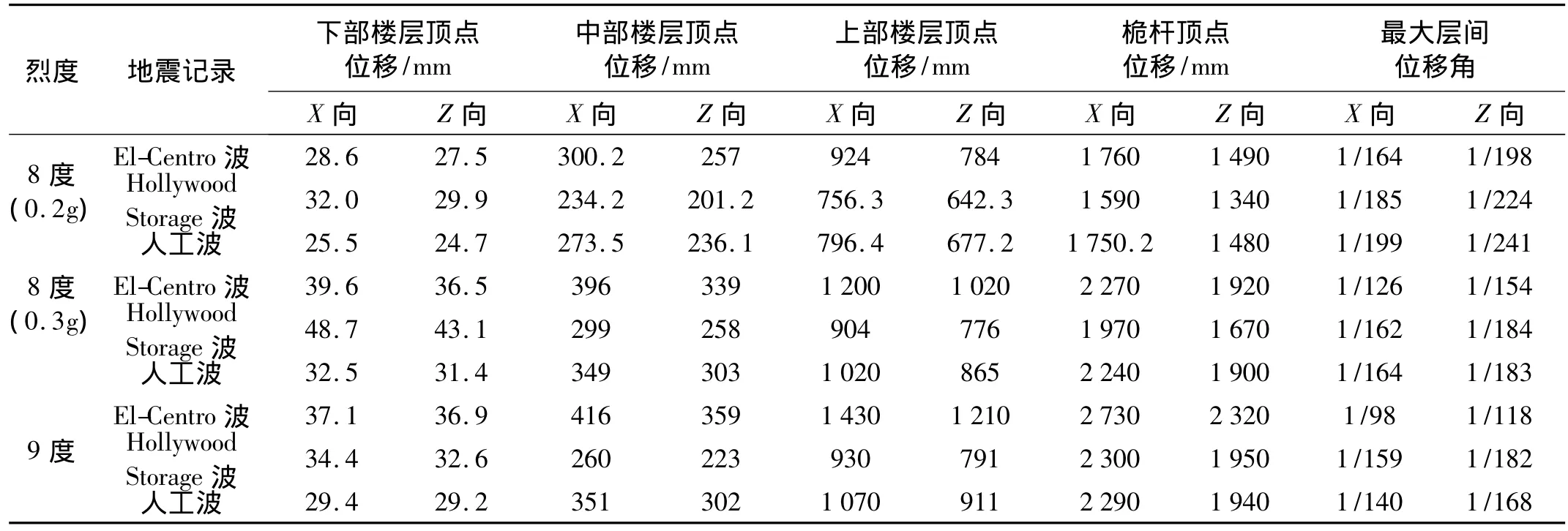
表5 不同设防烈度罕遇地震下结构的最大位移和最大层间位移角Tab.5 The maximum displacements and maximum interstorey drift ratios of the structure under the 8 degree(0.2g)，8 degree(0.3g)，and 9 degree rare earthquakes

为深入分析结构在大震作用下的弹塑性动力响应，图20对各关键点在不同设防烈度罕遇地震作用下的位移时程响应计算结果进行了比较。通过比较可见，9度弹塑性位移响应总体上大于8 度(0.3 g)，8 度(0.3 g)总体上大于8度(0.2 g)，但除了峰值时刻，其余部位有基本相等或稍微增大。这一现象表明在部分构件进入塑性状态后，结构部分位置承载能力和刚度的降低，不仅仅导致了内力和刚度的重新分布，也使结构的地震作用响应发生了变化。根据计算结果，可以判断由于结构刚度的降低，地震作用可以一定程度地减小。

6.2 构件应力及塑性发展

通过对结构应力最大值以及塑性发展历程的跟踪分析显示，在8度(0.2g)罕遇地震作用下，结构的塑性发展程度较弱，仅个别构件出现塑性，绝大部分时间和构件都处于弹性状态，且个别进入塑性构件的等效应力可恢复到弹性应力范围。在8度(0.3 g)和9度设防烈度罕遇地震作用下，在El-centro波作用下，结构中最早屈服构件为连接核心筒与外柱的连梁支撑，位于中部楼层段79m－83m高度;到4.46s时中部楼层段的塑性进一步发展:塑性应力范围内的构件数量增多，屈服构件类型也从连梁支撑发展到了框架梁支撑;到4.54 s，结构的下部楼层段连梁支撑也出现了塑性;到6.58 s，塑性应力范围内的构件类型不再局限于支撑，连梁端部以及与支撑相交位置也开始出现塑性。12.66 s为应力峰值时刻，最大等效应力为379 N/mm2，该构件为外柱间框架梁支撑，位于下部楼层段。此刻，下部楼层段连梁支撑以及个别框架梁端也进入了塑性应力范围，其他构件等效应力均处于弹性范围内。

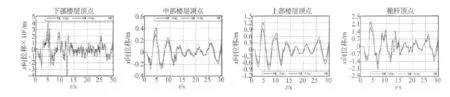
图20 不同设防烈度下El-Centro波作用下关键点X向水平位移时程曲线Fig.20 The X-directional displacement at the key points under the 8 degree(0.2 g)，8 degree(0.3 g)and 9 degree rare El-Centro earthquake

在Holleywood Storage波作用下结构中最早屈服的构件为连梁支撑，位于下部楼层段;到13.64 s下部楼层段的塑性进一步发展，从连梁支撑发展到了外柱间的框架梁支撑。随着卸载的进行，结构的等效应力慢慢减小。从14.4s开始，结构的下部楼层段框架支撑再次进入塑性应力范围，到15.06 s，塑性慢慢的发展到了下部楼层段的个别框架梁端上。

人工波作用下11.98 s中部楼层段的连梁支撑进入塑性;12.3 s时该构件的等效应力增加到了353 N/mm2;13.98 s时中部楼层段上层的连梁支撑也进入塑性应力，14.18s则发展到更多的连梁支撑上。人工波作用下结构的等效应力达到屈服的构件主要是中部楼层段的连梁支撑，其余构件的等效应力均处于弹性范围内。

通过上述分析，可见结构在各条波作用下结构的塑性发展进程如图21－图23所示。从图21－图23可以看出，虽然各条波作用下结构的塑性出现和发展有区别，但整体趋势来看，结构的塑性发展历程为连梁支撑－框架梁支撑－连梁端－框架梁端，结构的塑性发展较为合理，符合多道抗震防线的设防原则。

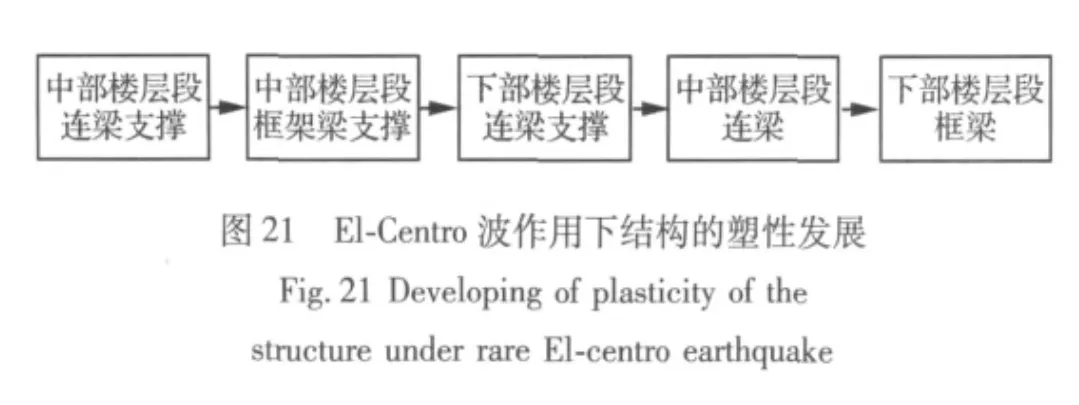
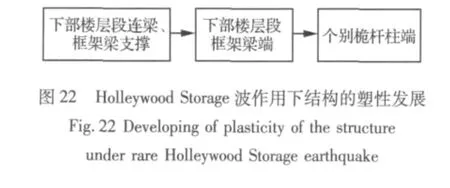
图23 人工波作用下结构的塑性发展Fig.23 Developing of plasticity of the structure under rare artificial earthquake

7 结论

采用ANSYS有限元软件，对NXTVT进行了动力特性、多遇地震和8 度(0.2 g)、8 度(0.3 g)、9 度罕遇地震作用下的地震反应计算和分析，得到的主要结论如下:

(1)NXTVT体型复杂，对其动力特性的计算分析表明，结构第一、第二阶振型以平动为主，第三阶为扭转振型，但伴随有一定的水平振动，扭平周期比满足规范要求但数值偏大，建议在减震控制设计时予以考虑。

(2)在多遇地震作用下，结构楼层段楼层的弹性层间位移角、塔顶最大水平位移均小于规范规定的限值，结构在多遇地震作用下的抗震性能满足规范要求。

(3)在8度(0.2 g)罕遇地震作用下，结构的楼层层间位移角最大值为1/164，在8度(0.3 g)罕遇地震作用下层间位移角最大值为1/127，在9度罕遇地震作用下层间位移角最大值为1/98，均满足《建筑抗震设计规范》(GB50011－2002)规定的1/50限值要求。

(4)在8度(0.2 g)罕遇地震作用下，宁夏电视塔结构的塑性发展程度较弱，仅个别构件出现塑性，绝大部分时间和构件都处于弹性应力状态;在8度(0.3 g)9度和罕遇地震作用下，结构的塑性发展较8度(0.2 g)有很大程度的提高，塑性不仅出现在支撑构件上，框架梁端、连梁也出现了构件部分截面进入塑性的情况;但整体上，外柱、核心筒及网格筒基本处于弹性状态，结构满足“大震不倒”的抗震设防要求。

(5)整体趋势来看，结构的塑性发展历程为连梁支撑－框架梁支撑－连梁端－框架梁端，结构的塑性发展较为合理，符合多道抗震防线的设防原则。

(6)结构在8度(0.3 g)和9度罕遇地震作用下，结构最早屈服的构件都出现在中部楼层段，该部位是结构最薄弱的部位，该位置恰好在结构立面上的细腰段，应特别予以加强处理。

［1] 王肇民，马人乐.塔式结构［M] .北京:科学出版社，2004.

［2] 王雪亮，瞿伟廉，刘 晖.广州新电视塔的动力特性有限元分析［J] .武汉理工大学学报，2007，29(1):142－156.

［3] 林同炎，斯多台斯伯利.结构概念和体系［M] .北京:中国建筑工业出版社，1999.

［4] 王元清，黄 怡，石永久，等.超高层钢结构建筑动力特性与抗震性能的有限元分析［J] .土木工程学报，2006，39(5):65－71.

［5] 马人乐，赵 林，何敏娟.大型超高钢结构电视塔抗震性能分析［J] .同济大学学报，2007，35(10):1310－1315.

［6] 何敏娟，梁 峰，马人乐.大型超高钢结构电视塔模拟地震振动台试验研究.振动与冲击，2010，29(1):77－80.

［7] 中华人民共和国行业标准.高层建筑混凝土结构技术规程(JGJ 3－2002)［S] .北京:中国建筑工业出社，2002.

［8] 中华人民共和国国家标准.建筑抗震设计规范(GB 50011－2001)［S] .北京:中国建筑工业出版社，2008.

［9] 杨 溥，李英民，赖 明.结构时程分析法输入地震波的选择控制指标［J] .土木工程学报，2002，33(6):33－37.

［10] 中华人民共和国国家标准.高耸结构设计规范(GB 50135－2006)［S] .北京:中国计划出版社，2007.