基于线性规划的直升机旋翼性能优化分析
蔡 伟,曹金华,吴奎发
(1.中航工业昌河飞机工业集团公司,江西景德镇 333002;2.陆航驻景德镇地区代表室,江西景德镇 333000)
0 引言
直升机的旋翼(气动)性能对全机性能优劣起着决定性的作用,优化旋翼几何外形以改善其性能是直升机界非常重视的问题[1]。在旋翼设计过程中,常常首先只确定旋翼的总体参数,而桨叶具体的几何参数(例如,弦长,扭转角,尖削值等)的确定,则需要通过不断地进行尝试以达到性能指标,这是一个耗时且繁琐的过程。若能在准确计算旋翼性能的基础上,通过选用某种优化算法对其进行优化分析,那么旋翼设计过程将得到简化。因而,开展直升机旋翼性能的优化技术研究和探讨具有一定的理论和现实意义。
进行旋翼性能优化分析的首要前提是对旋翼性能的准确计算。在过去,计算旋翼流场及性能的常用方法是动量理论、固定尾迹方法及预定尾迹方法,但它们因各自的局限性,很难在旋翼性能预估技术中得到有效应用[2]。而自由尾迹方法具有良好的旋翼尾迹形状模拟能力,是一种更准确且物理上正确的方法[3]。此外,选择一种满足具体要求的优化算法同样重要。随着计算机技术的快速发展,线性规划方法更趋成熟,应用更为广泛,成为解决工程优化问题的一种实用方法。作为求解线性规划的常用方法,单纯形法试图通过有限次迭代得到最优解,可同时满足鲁棒性和有效性的要求[4]。
计算旋翼性能的关键在于对其尾迹结构的捕捉[5]。为此,本文拟采用松弛类自由尾迹方法对悬停状态的旋翼尾迹结构进行捕捉并计算此状态的旋翼性能。其中,采用二阶升力线模型模拟桨叶空气动力的作用,而尾迹模型则采用当今国际上应用较多的卷起桨尖涡模型。在计算旋翼性能的基础上,将性能优化问题进行线性化假设和处理,并采用单纯形法对其进行优化分析。从已公开发表的文献来看,国外开展的旋翼性能优化计算主要集中在悬停状态。而在国内,对旋翼性能进行优化分析的工作开展得很少。因此,本文通过耦合线性规划和自由尾迹方法对悬停旋翼性能进行优化分析,在国内是一种新的尝试。
1 计算模型和优化方法
1.1 桨叶气动模型和尾迹模型
采用二阶升力线模型模拟桨叶空气动力的作用,桨叶附着涡布置在四分之一弦线上,而相应的单元涡格控制点则布置在四分之三弦线中点处。每一小段桨叶附着环量规定为常值,它们沿桨叶径向的变化引起尾随涡在桨叶后缘拖出,并以当地速度自由移动。而桨叶附着环量沿旋转方位角的变化则引起脱体涡的逸出。
在本文建立的卷起桨尖涡模型中,忽略桨根涡对空间点诱导速度的贡献,只计入桨尖涡的影响,并且假设桨尖涡的卷起服从Betz卷起规则[6]。将整个尾迹模型分为近尾迹和远尾迹部分。近尾迹由尾随涡和脱体涡构成,而远尾迹为向下游运动的桨尖涡。旋翼下洗流场中空间点的当地速度包括由桨叶附着涡、尾随涡和桨尖涡共同诱导产生的速度。旋翼自由尾迹在它们的共同作用下完全自由地在流场中移动(如图1所示)。
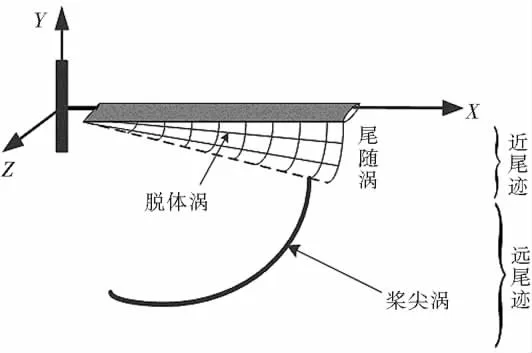
图1 卷起桨尖涡旋翼自由尾迹模型示意图

采用有限差分方法离散涡线控制方程之后,再进一步对其进行数值迭代求解,迭代方法选用由赵景根等人[7]提出的“预测-校正-松弛”组合迭代方法。
1.2 旋翼性能的求解方法
直升机悬停状态下旋翼消耗的功率主要包括诱导功率Pi和型阻功率Po,即

式中Pv表示悬停状态下旋翼消耗的总功率。
得到桨叶各段的附着环量后,便可确定桨叶剖面的气动力,进而求出旋翼拉力和扭矩。
由Joukowski定律,桨叶单位长度上的升力为

式中,ρ为空气密度,Wi是剖面来流速度,Γi是第i段桨叶微元的附着涡环量值。
由此,将各剖面升力分解得到翼型拉力并沿展向求和,即可确定旋翼的拉力。将剖面升力与到旋翼轴的向量做矢积,并取平行于旋翼轴的矢积分量进行求和,即可得到诱导功率。
查询相关二元翼型数据表确定桨叶剖面型阻系数Cd,并求解相应的剖面型阻,从而求和确定旋翼的型阻功率系数。
1.3 旋翼性能的优化分析方法
由于桨叶面元的法向诱导速度来自附着涡、尾随涡和桨尖涡的共同贡献,并要求满足面元法向合速度为零的边界条件,且尾迹形状收敛,悬停旋翼性能中的拉力和诱导功率均可由各桨叶微段的环量值线形表达。而型阻功率所占的比例较小,也可作近似的线性处理。至此,可近似将悬停旋翼气动性能线性表达为

其中,{τ}为桨叶各分段的环量值,[Pτ]和[Tτ]各为相应的计算旋翼功率和旋翼拉力的影响系数矩阵。
在讨论优化问题前,需要引入设计变量。通常来说,可作为设计变量的桨叶几何参数包括扭转角、弦长、尖削角、后掠角等,本文选择桨叶扭转角分布作为优化分析的设计变量,而将旋翼消耗的功率作为目标函数。在旋翼拉力保持不变的情况下使得消耗的旋翼功率最小,即要求在ΔT等于零的同时使得ΔP达到最大。另外,为保证引入桨叶结构微调后,依旧维持桨叶切向流的边界条件及旋翼尾迹的收敛,需要引入以下约束函数
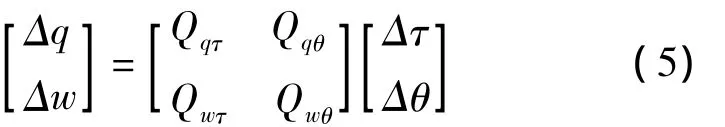
式中,Δq、Δw分别表示尾迹位置和桨叶面元法向速度的扰动量,Q矩阵是计算Δq和Δw所需的影响系数矩阵,而且Δq和Δw这二项扰动都应为零。
每次调用优化算法前都需要对旋翼桨叶新扭转分布情况下的尾迹进行更新,并重新确定相应的旋翼拉力系数和功率系数,将其与之前的系数的差值作为下一轮优化计算中约束函数及目标函数方程设计变量的系数。图2给出了本文中进行旋翼性能优化计算的主要步骤。

图2 悬停旋翼性能优化计算的流程图
需要指出的是,由于旋翼气动性能的计算本身是非线性的,因而将这一过程做线性处理,是有一定误差的。另外,本文计算得到的旋翼性能优化值未必是理论上的最优值,这主要是由于计算过程里做了一些简化、假设以及优化计算时间的限制等。
2 算例
选用文献[1]中提及的一组旋翼参数,并应用本文建立的旋翼性能线性优化方法对该旋翼的悬停气动性能进行优化分析。旋翼的基本参数如下:半径4.6m,弦长 0.3m,旋翼转速 40rad/s,桨叶翼型是NACA0012,优化前的桨叶采用线性扭转,扭转角为-7°。下面将对四片桨叶的情况进行悬停旋翼性能优化分析。
取旋翼尾迹10周,其中畸变(自由)尾迹2周。为了在保证一定计算精度的前提下减少计算时间,将桨叶沿展向按正弦函数方式分为14段。经计算,调用10次优化程序后,旋翼消耗的诱导功率得到有效减小。

图3 优化前后扭转角分布情况(初始CT=0.00448)
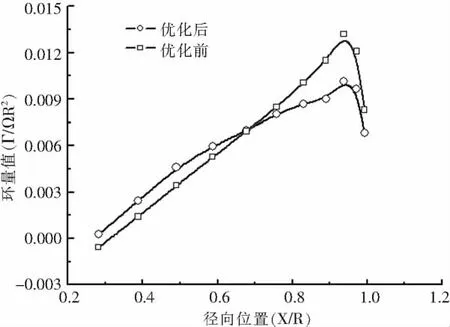
图4 优化前后环量分布情况(初始CT=0.00448)
优化前将旋翼总距设定为8°,此时相应的旋翼拉力系数为0.00448,悬停效率是0.608。进行优化计算后,旋翼悬停效率提高了6.3%,达到0.646。图3和图4分别比较了优化前后桨叶展向扭转角和环量分布的变化情况。从图中可以看出,桨叶安装角不再呈线性分布,而环量分布也更加“均匀”。该优化算法的实质是,将桨叶外段的载荷“转移”到内段上,这样就在保持旋翼拉力不变的情况下减小旋翼扭矩(旋翼诱导功率)。从图3中还可以看到,桨叶径向约75%以内安装角增大明显,而外端靠近桨尖处安装角迅速减小。从环量的分布图中也可说明这一点,即增加了桨叶内段的载荷,相应减小了靠近桨尖处的载荷。
3 结束语
本文通过耦合线性规划和旋翼自由尾迹方法,对悬停状态的旋翼气动性能进行了优化分析,可得到以下结论:
1)通过建立基于线性规划的旋翼性能优化分析模型,实现了悬停状态旋翼桨叶几何参数的优化,可提高旋翼的悬停效率,改善旋翼气动性能;
2)以四片桨叶模型旋翼为算例,验证了该旋翼性能优化分析模型的有效性。桨叶扭转角分布在优化调整后,桨叶环量值和剖面载荷沿展向分布更加均匀;
3)本方法适用于直升机悬停状态的旋翼性能优化设计,单纯形法的求解思想简单实用,易于编程实现,具有一定的工程应用价值。
[1]Quackenbush T R,Wachspress D A,Kaufman A E.Optimization of Rotor Performance in Hover Using A Free Wake Analysis[J].Journal of Aircraft,1991,28(03):200-207.
[2]王适存,徐国华.直升机旋翼空气动力学的发展[J].南京航空航天大学学报,2001,30(3):203-21.
[3]Bagai A,Leishman J G.Rotor Free Wake Modeling U-sing a Relaxation Technique Including Comparisons with Experimental Data[J].Journal of the American Helicopter Society,1995,40(03):29-41.
[4]江道琪,何建坤,陈松华,编:实用线性规划方法及其支持系统[M].北京:清华大学出版社,2006.
[5]Landgrebe A J,Cheney M C.Rotor Wakes-Key to Performance Predictions[R].AGARD CPP-111,1972.
[6]Rossow V J.On the Inviscid Rolled-Up Structure of Lift Generated Vortices[J].Journal of Aircraft,1973,10(11):647-650.
[7]赵景根.直升机旋翼/机身气动干扰的研究[D].南京:南京航空航天大学,2001.

