几种特殊类型二重积分的计算技巧

赵 赫

(北京林业大学 林学院, 北京 100083)

几种特殊类型二重积分的计算技巧

赵 赫

(北京林业大学 林学院, 北京 100083)

二重积分是高等数学的重点，也是难点，计算较为繁琐，有的二重积分需要一定的技巧才能求出．探讨了积分区域关于坐标轴对称、关于直线对称、积分区域是圆的一部分等特殊区域上二重积分的计算技巧，讨论了几类特殊被积函数二重积分的选择积分顺序的问题，研究了如何用轮换法求二重积分．

二重积分；积分区域；被积函数

众所周知，计算二重积分的一般原则是将二重积分化为二次积分(即累次积分)加以计算．求积的困难主要来自2个方面，一是被积函数的复杂性，二是积分区域的多样性．不同顺序二次积分计算的难易程度往往是不相同的，有时选错积分顺序导致积分无法计算，有的二重积分必须通过换元才能求出．

通过自己做二重积分习题时的一些心得体会，再结合所查资料以及老师指导，这里总结了几类特殊二重积分计算技巧．

1 积分区域关于坐标轴对称

设积分区域为D

1) 当D关于y轴对称时

2) 当D关于x轴对称时

例1 设D为以点(1,1)， (−1,1)， (−1,−1)为顶点的三角形，D1为D在第一象限部分．试将∫(xy+cosx siny)dx d y 化为D1上的积分．

解 积分区域如图所示，被积函数中xy是x的奇函数，也是y的奇函数．cosx siny是x的偶函数，是y的奇函数．为利用奇、偶函数积分的性质，需将D分为对x轴或对y轴对称的域．为此作直线y=−x，即连结点(0,0)， (−1,1)，将D分为4个区域，其中，D1，D2关于y轴对称，D3，D4关于x轴对称

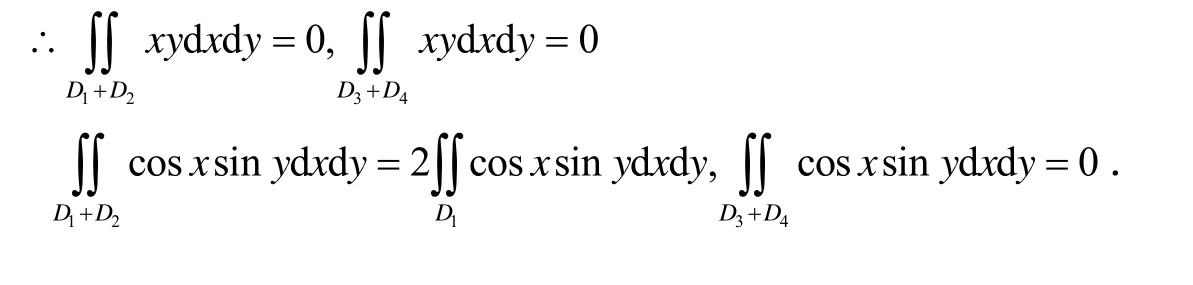
图1 例题1

2 积分区域关于直线yx=对称

当积分区域关于直线y=x对称时，有些二重积分可用轮换坐标的方法来简化计算．轮换坐标是换元法的一种特殊形式，即将x，y互换．将x，y更换顺序后，相当于将坐标轴重新命名，积分区域没有发生变化，则被积函数作相应变换后，积分值不变．

解 D的边界曲线的极坐标方程为r=cosθ+sin θ

积分区域关于直线y=x对称，根据轮换坐标对称性，将x、y互换，则

2 例题2

解 积分区域关于直线xy=对称，根据轮换坐标对称性，将x、y互换，则

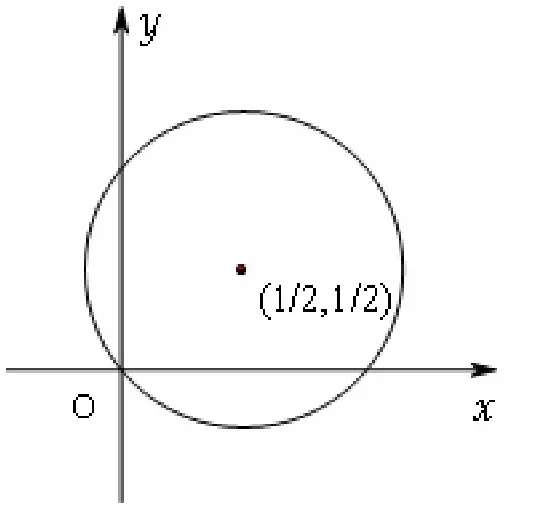
3 积分区域是圆的一部分

若积分区域是圆的一部分时，常用极坐标变换计算二重积分．即

图3 例题4

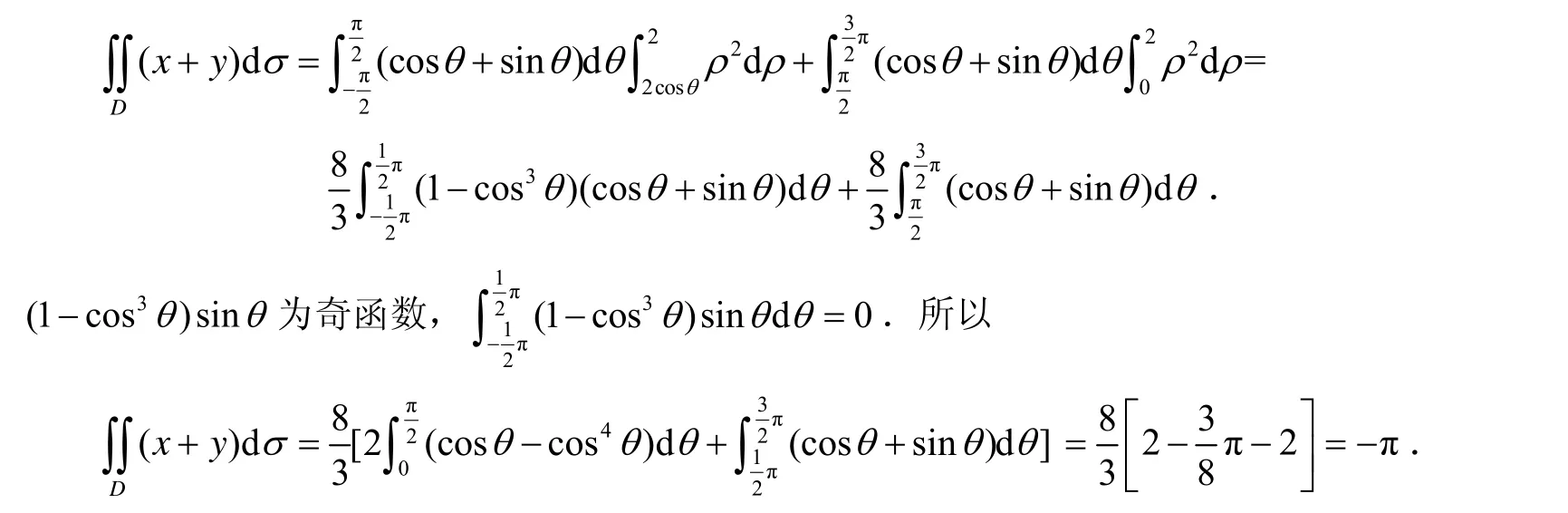
4 被积函数的原函数不是初等函数

若被积函数只与y(或x)有关，并且原函数不是初等函数，则只有化成先对x(或y)后对y(或x)的积分．如则只能化成先对y后对x的二次积分．

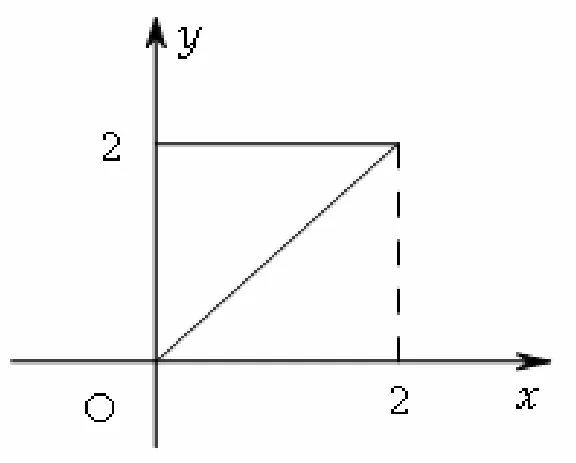
图4 例题5

综上所述，二重积分的计算方法是有规律可循的．总体上，二重积分的计算思路是先化重积分为累次积分，在做重积分题目时，要根据积分区域和被积函数的特点，灵活选择合适的方法，使计算过程最大程度的简化．

Several Calculating Techniques of Special Double Integral

ZHAO He

(College of Forestry, Beijing Forestry University, Beijing 100083, China)

Double integral is the important and difficult point in advanced Mathematics. Its calculation is very complicated and some require certain techniques. This paper discusses some special calculating techniques concerning coordinates axis symmetry, beeline symmetry, and integral domain being part of a circle, etc. It analyzes the integral option order of double integral of some special integrand. It also studies how to calculate double integral with rotation method.

double integral; integral domain; integrand

O172.2

A

1673-2065(2011)04-0010-03

(责任编校：李建明 英文校对：李玉玲)

2011-03-26

赵 赫(1990-),女,河北衡水人,北京林业大学林学院学生.