一类三阶边值问题单调迭代解的存在性

邹序焱，陈世群

(宜宾学院数学学院，四川 宜宾 644007)

文献［1］应用锥拉伸与锥压缩定理以及Leggett–Williams不动点定理，证明了下列边值问题:

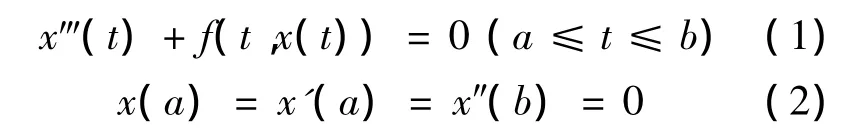
至少存在一、二、三和无穷多个单调正解.

文献［2］利用范数形式的锥拉伸与锥压缩不动点定理讨论了下列边值问题正解的存在性:

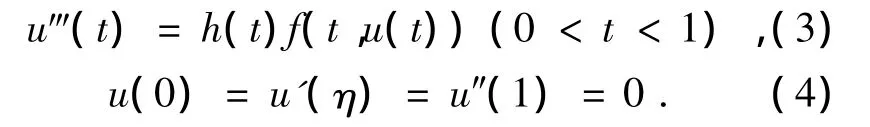
三阶多点边值问题正解的存在性，在我们生活实践中有着广泛的应用，也引起了广大学者的关注［3－7］.文献［3］利用锥压缩与锥拉伸定理考查了一类三阶非线性周期边值问题正解的存在性.

本章应用单调迭代技术讨论了下列边值问题:

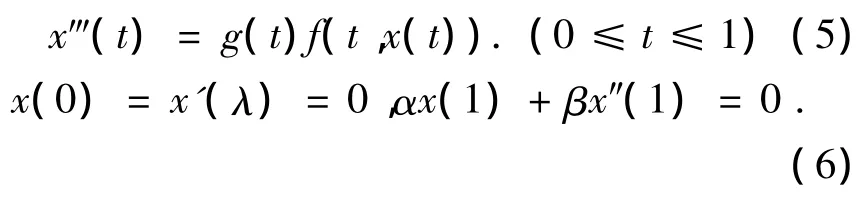
其中，f:［0，1］×［0，+∞)→［0，+∞)是连续函数，g:［0，1］→［0，+∞)也是连续函数且满足，且β＞0.在边值问题不要求有上下解存在的情况下，应用单调迭代技术从简单函数开始构建出连续的函数序列，使它趋近边值问题的正解.

1 引理

引理1［8］边值问题(5)+(6)的解当且仅当它满足下面的积分方程

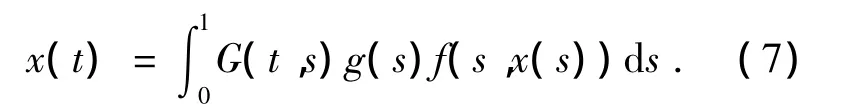
其中

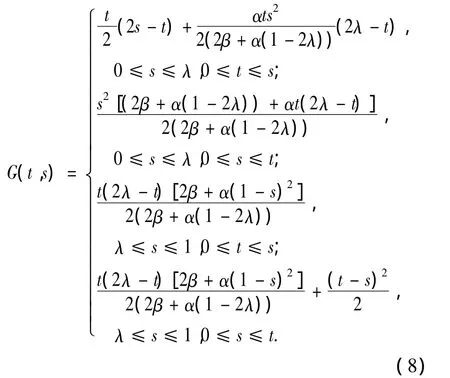
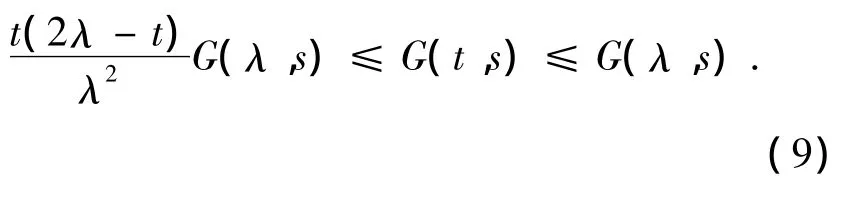
引理2［9］设{xn}是单调序列且为相对列紧集，则{xn}是收敛序列.更进一步，若{xn}是单调增序列，则有 xn≤ x*(n=1，2，3…)，其中x*是{xn}的极限，若是减序列，则x*≤xn(n=1，2，3…).

为了证明边值问题存在正解，我们定义

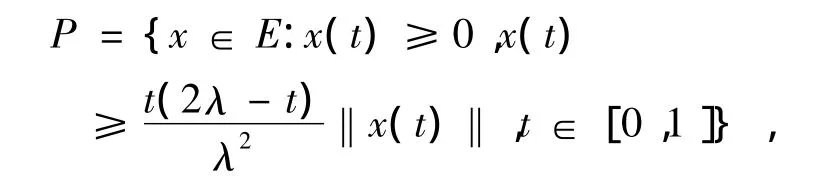
经计算满足锥的定义.

算子

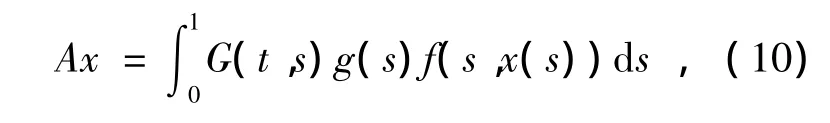
对于任意x∈P，根据(9)式得

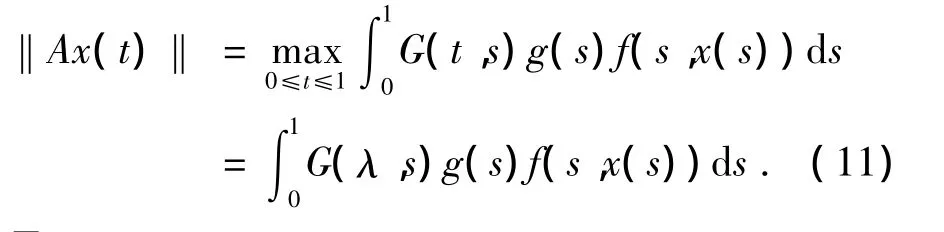
且

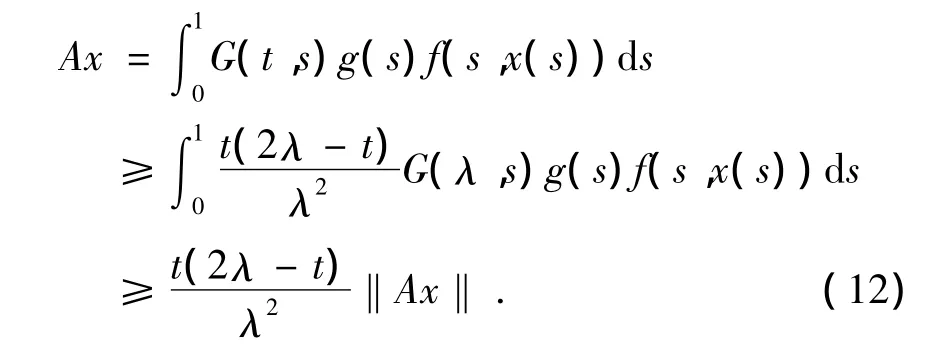
由(12)式知，算子AP⊂P.很容易验证算子A:P→P是全连续算子，所以算子A在P中的不动点即为边值问题(5)+(6)的解.

2 主要结果及证明

定理1 假设存在常数a＞0，且

(H1)f(t，x1)≤ f(t，x2)，对所有的0 ≤ t≤1，0≤x1≤x2≤a;

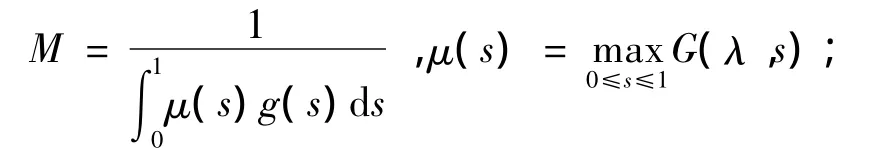
(H3)f(t，0)不恒等于零，则边值问题(5)+(6)存在正解v*和w*，满足:

0＜v*(t)≤a，0＜w*(t)≤a，

且

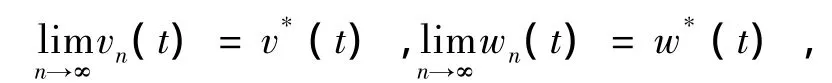
其中:v0(t)=0，w0(t)=a;及

vn(t)=(Avn-1)(t)，wn(t)=(Awn-1)(t)，

其中 n=1，2，3… .

证明

(i)定义Pa={x∈P，‖x‖≤a}，对任意的x∈Pa，由(10)式定义的算子有

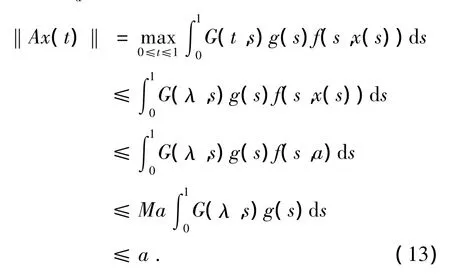
由(13)得算子A:Pa→Pa.

(ii)假设 v0(t)=0，vn=Avn-1，n=1，2，3….因为算子 A:Pa→ Pa，所以 vn∈ A(Pa)⊂Pa，设任意的 x(t)，x1(t)，x2(t)∈ Pa，且有 0 ≤x1(t)≤x2(t)≤a，以及G(t，s)≥0，g(s)≥0得

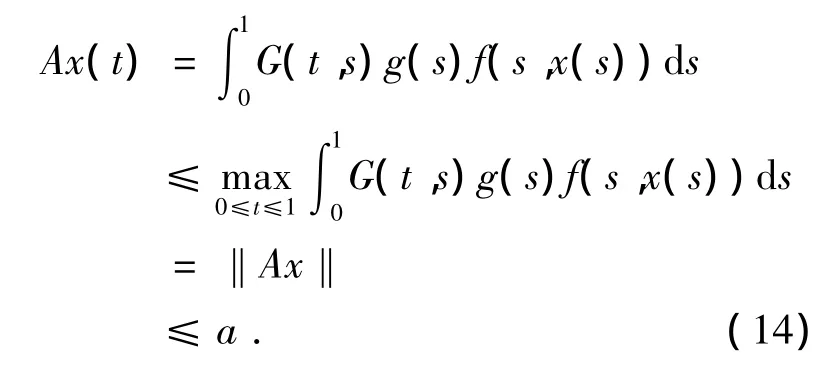
且Ax(t)≥0.

由(H1)得

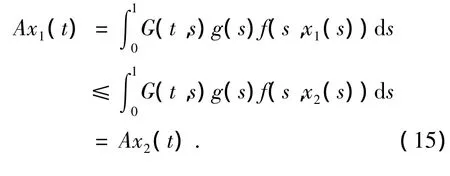
即

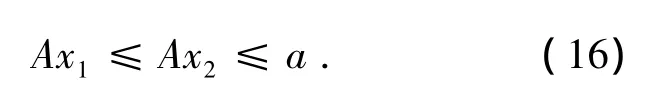
由v0=0，得a≥v1(t)=(Av0)(t)≥0=v0(t).由(13)及(16)式有

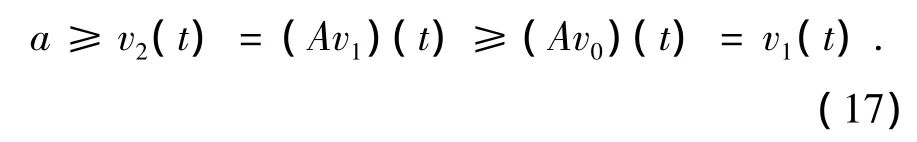
依次迭代得:

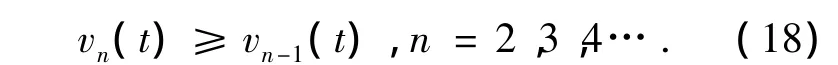
(iii)假设 w0(t)=a，wn=Awn-1，n=1，2，3….由于a ＞ 0，且a∈P，a∈Pa所以

w1(t)=(Aw0)(t)≤a=w0(t).由(15)式

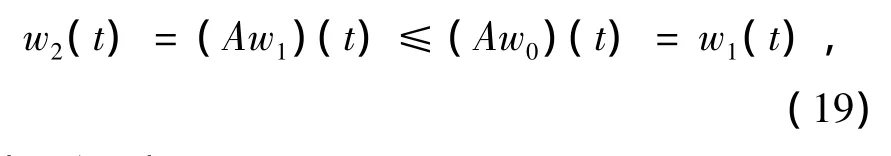
从而得到:

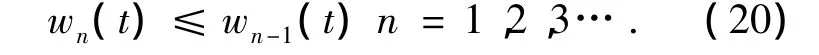
由于以上证明不能肯定v*≠w*或v*=w*，所以不能肯定算子A在Pa中存在两个正解，但能肯定算子A在Pa中存在至少一个正解.因此边值问题(5)、(6)存在正解.

3 举例

考虑下列边值问题:

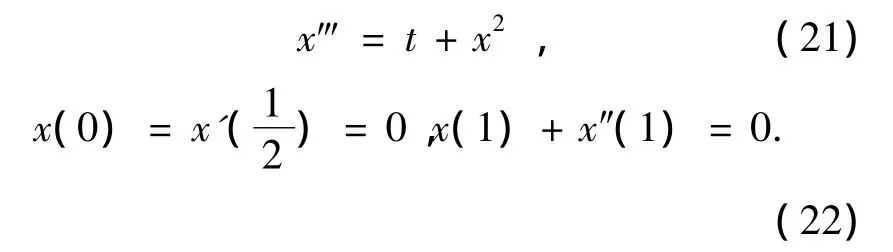
其中:g(t)=1，f(t，x)=t+x2，，α =1 ＞0，β=1 ＞0.取a=1，经计算得M=3，经验算它满足定理1的所有条件.因此边值问题(21)+(22)存在正解v*和w*，且

0 ＜ v*(t)≤ a，0 ＜ w*(t)≤a，t∈(0，1).存在两个单调迭代序列和，使得

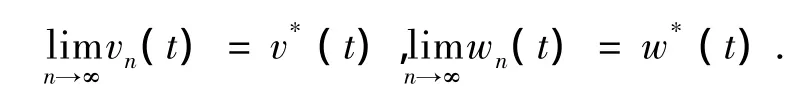
其中:vn=Avn-1，wn=Awn-1，v0(t)=0，w0(t)=a.

［1］Liu Zeqing，Lokenath Debnathb，Shin Min Kangc.Existence ofmonotone positive solutions to a third order two－point generalized right focal boundary value problem［J］.Computers and Mathematics with Applications，2008，55(3):356 – 367.

［2］Liu Z，Ume J，Kang S.Positive solutions of a singular third order two－ point boundary value problem［J］J.Math Anal Appl，2007，326:589 －601.

［3］Chu Jifeng，Zhou Zhongcheng.Positive solutions for singular non－linear third－order periodic boundary value problems［J］.Nonlinear Analysis ，2006(64):1528－1542.

［4］Guo Lijun，Sun Jianping，Zhao Yahong.Existence of positive solutions for nonlinear third－order three pointboundary value problems［J］.Nonlinear Analysis，2008(68):3151–3158.

［5］Grossinho M R，Minhós FM，Santos A I.A third －order boundary value problem with one－sided Nagumo condition［J］.Nonlinear Analysis，2005(63):247－ 256.

［6］Yao Qingliu.Positive solutions of singular third－order three － point boundary value problems［J］.J.Math.Anal.Appl.，2009，354:207 – 212.

［7］Alex P，Palamides，George Smyrlis.Positive solutions to a singular third－order three－point boundary value problem with an indefinitely signed Green’s function［J］.Nonlinear Analysis，2008(68):2104–2118.

［8］Douglas R Anderson.Green’s function for a third order generalized right focal problem［J］.Journal of Mathematical Analysis and Applications.2003，288(1):1 –14.

［9］郭大钧，孙经先，刘兆理.非线性常微分方程泛函方法［M］.济南:山东科学技术出版社，1995:10－15.