一类椭圆型方程弱解的正则性

狄华斐，周道军，郑治波

(1.云南民族大学数学与计算机科学学院，云南 昆明 650500;2.云南师范大学数学学院，云南 昆明 650092)

现代椭圆型方程问题的可解性的研究总是在合适的泛函空间中考虑其弱解的性质，所以sobolev空间的引进为这一研究提供了有效途径［1－2］.通过 sobolev 空间，我们可以在更广泛的函数类中寻求问题的解，这样可解性的问题变得就容易多了.这种解往往就称为“弱解”或“广义解”.

本文讨论椭圆型方程:

在一定的条件假设下弱解的正则性问题.近年来，这类椭圆型方程很多学者已经对它进行了广泛的研究［2－4］.这些文献假设算子 L的系数 aij，bi，c是光滑的.在本文中，我们对L的系数的范围进一步放宽，在这里只要求aij∈Cm+1(U)，bi，c∈Wm，∞(U)，则得到与文献［2］同样的结论.

我们假设U⊂Rn是一个有界开集.u∈H10(U)是椭圆型方程Lu=f in U的一个弱解，在这里L拥有散度形式:

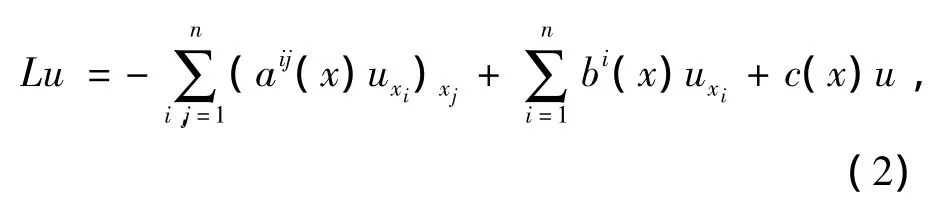
并且偏微分算子L是一致椭圆型算子，即存在常数θ＞0，使得:

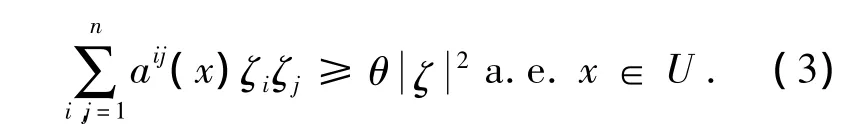
其中ζ∈Rn，并且对方程中的系数aij，bi，c进一步做出额外的假设.双线性泛函B［，］是通过椭圆型算子L定义的，即:

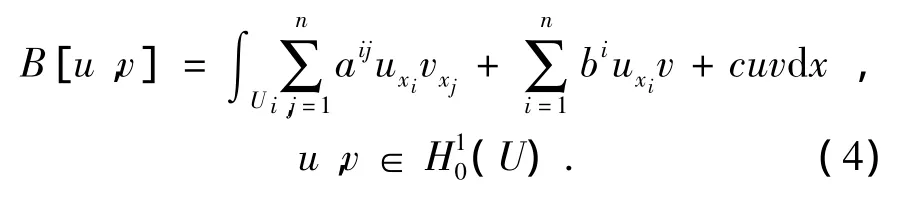
1 主要结果

本文的主要结论:

定理1 设m是一个非负整数，并且L的系数满足:

且

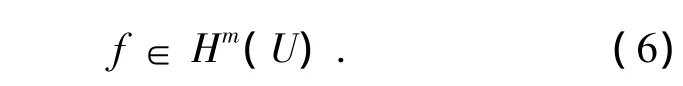
进一步假设u∈H1(U)是椭圆型方程Lu=f in U的一个弱解，则:

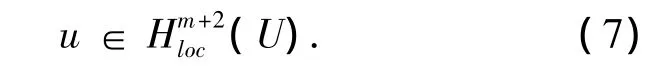
对于任意的V⊂⊂U(即V是U的紧子集)，有:

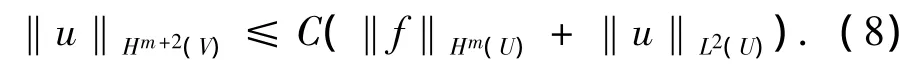
这里，常数C依赖于U，V及算子L的系数.

2 几个要用到的结论

注意:在这里(，)代表的是 L2(U)上的内积.

定理2 设m是一个非负整数，并且L的系数满足 aij，bi，c∈Cm+1(U)，f∈Hm(U)，如果 u∈H1(U)是椭圆型方程Lu=f in U的一个弱解，则u∈(U)且对于任意的V⊂⊂U(即V是U的紧子集)有:

这里常数C依赖于U，V及L的系数.

注意:定理 2中要求 L的系数:aij，bi，c∈Cm+1(U)(证明的过程参考文献［2］).在定理1中，我们对L的系数的范围进一步放宽，只要求aij∈ Cm+1(U)，bi，c∈ Wm，∞(U)，则可得到同样的结论.

3 定理1的证明

1)(7)、(8)结论的证明，我们采用归纳法.首先讨论m=0的情况，即L的系数满足aij∈C1(U)，bi，c∈ L∞(U)，f∈ L2(U). 如果 u ∈H1(U)是椭圆型方程Lu=f in U的一个弱解，则，且对于任意的V⊂⊂U(即V是U的紧子集)，有

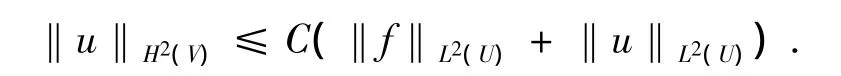
常数C依赖U，V及L的系数.

2)固定任意一个开集 V⊂⊂ U，使得dist(∂V，∂U)= δ＞ 0(其中δ是一个常数)，选择一个开集W，使得V⊂⊂W⊂⊂U，接着选择一个光滑函数ζ(x)满足:

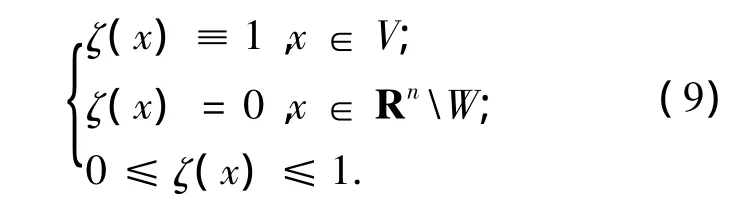
在这里，ζ(x)为一个截断函数(ζ(x)的取法见文献［6］).

3)因为u是椭圆型方程Lu=f in U的一个弱解，∀v∈(U)，B［u，v］ =(f，v).因此:

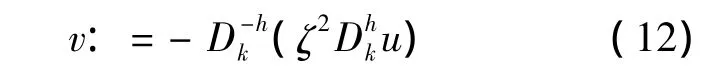
我们将表达式写成:

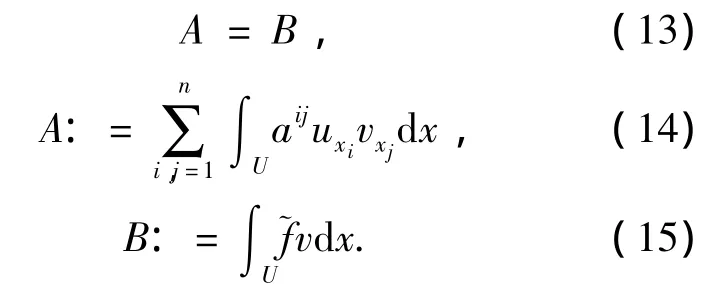
5)对A进行估计

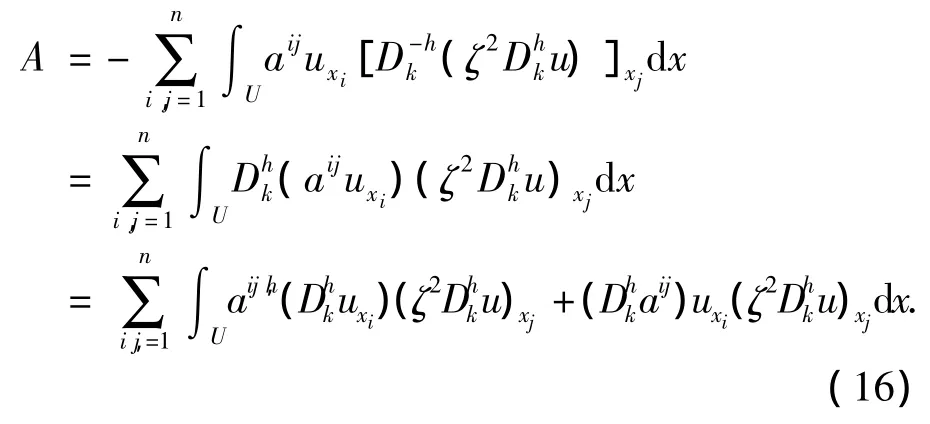
在这里用到的公式有:

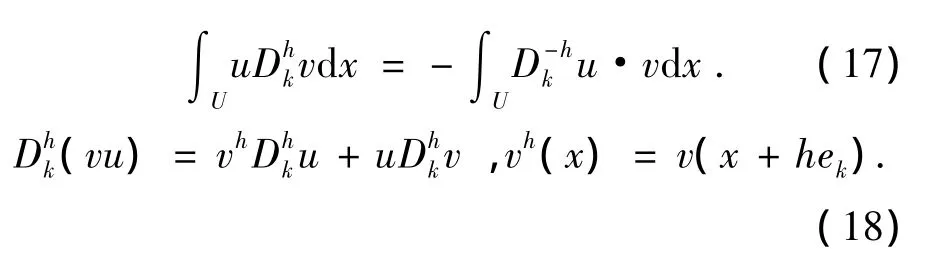
返回到(16)，我们发现:

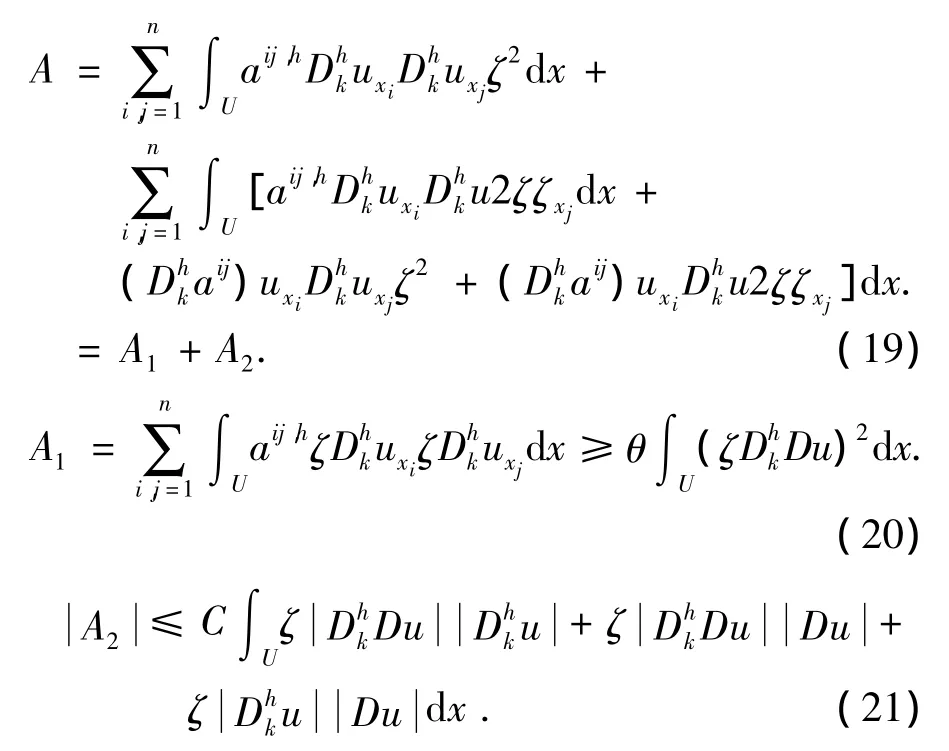
这里要求aij∈C1(U).

应用柯西不等式，整理得:

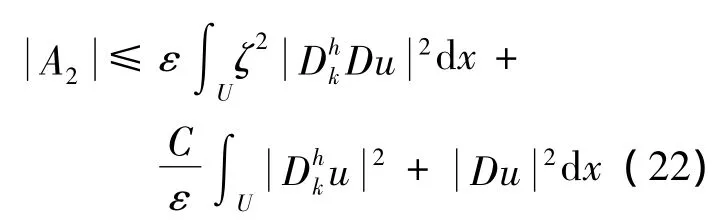
上式用到了(9)式中ζ(x)的定义.

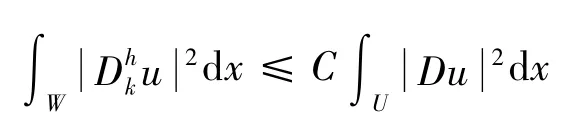
(见参考文献［2］§5.8.2 中的定理3)

因此，可得不等式:

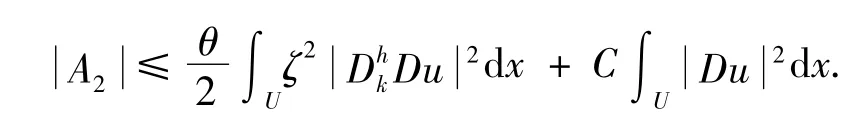
6)对B 的估计，综合(11)、(12)、(15)得到:

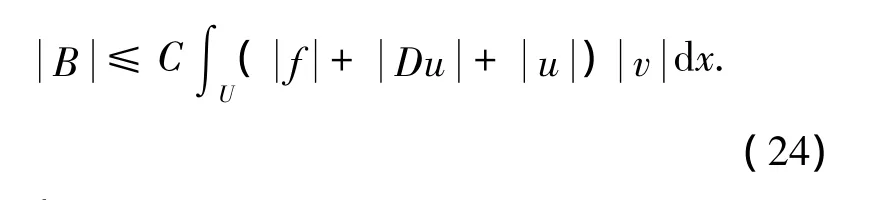
又因为:

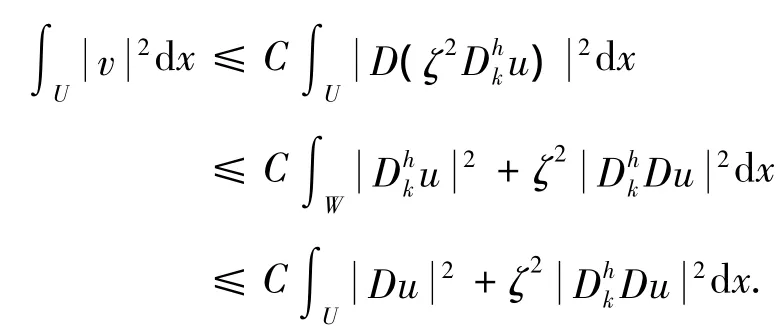
所以由ε的柯西不等式和(24)式得:

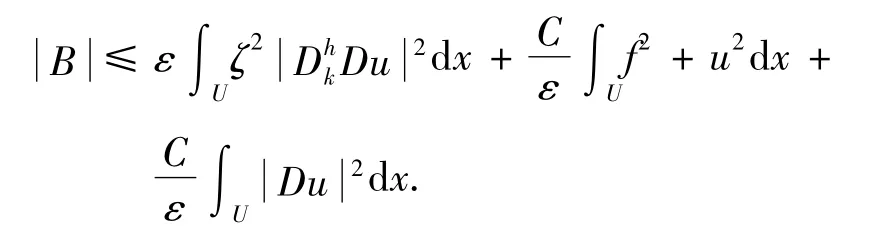
综合(13)、(23)、(25)得:

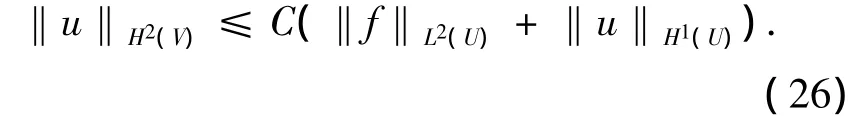
7)如果V⊂⊂W⊂⊂U，如同步骤2)～6)的方法可得:

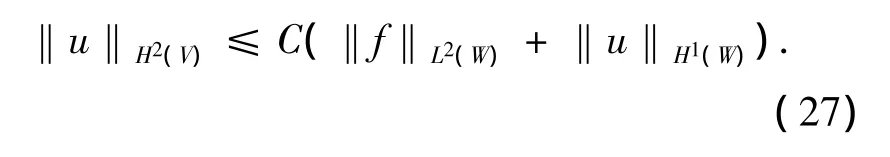
常数C与V，W及算子L的系数有关.

选取一个新的截断函数:

取v=ζ2u，则通过计算得:

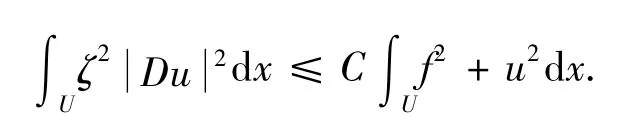
所以有:

又综合(27)式可得

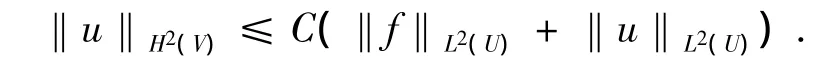
8)假设m=k+1(为一个非负整数)时结论成立.

9)那么当m=k+2时，即在aij∈Ck+2(U)，bi，c∈ Wk+1，∞(U)的假设前提下，同时 u ∈H1(U)是椭圆型方程Lu=f in U的一个弱解.

接着通过整理(29)式有:

其中

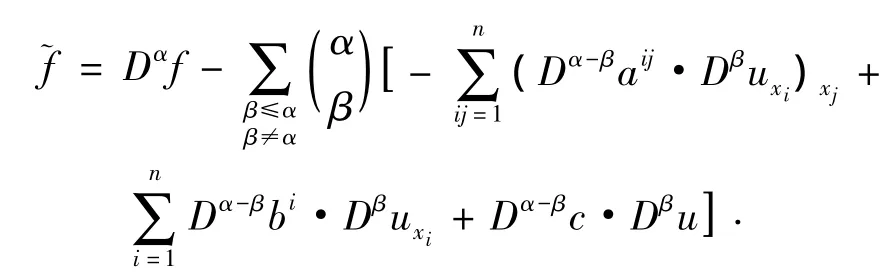
由弱导数的定义［6］，在中只要求:aij∈Ck+2(U)，bi，c ∈ Wk+1，∞(U)，就可得到 (L，)=).又结合步骤8)中的假设，我们可得到∈L2(W)且

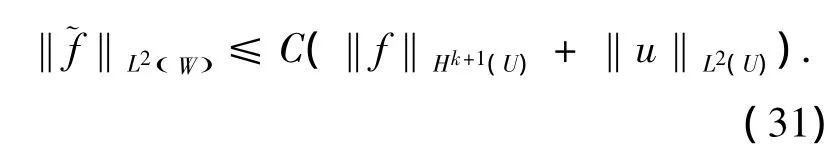
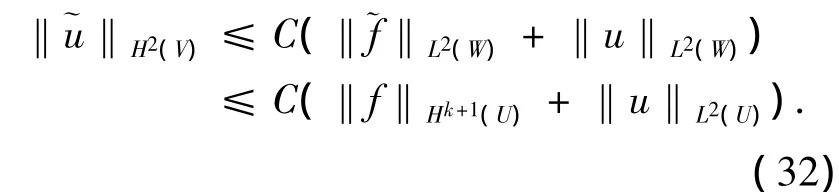
4 结论

在这篇文章中，我们对椭圆型算子L的系数范围进一步放宽，只要求 aij∈ Cm+1(U)，bi，c∈Wm，∞(U)，并且函数u在边界∂U上不做出任何假设，然后通过一定的技巧和方法，讨论了一类椭圆型方程弱解的内部正则性，给出了定理1的结论.

［1］李开泰，马逸尘，王立周.广义函数和 Sobolev空间［M］.西安:西安交通大学出版社，2008:67－83.

［2］Lawrence C Evans.Partial differential equations［M］.Rhode Island，1988:308－317.

［3］陈亚浙，吴兰成.二阶椭圆型方程与椭圆型方程组［M］.北京:科学出版社，1991:1－14.

［4］Zhang Yunzhang ，Yang Ganshan.Existence and regularity ofweak solutions for the biharmonic equation with complete second order derivative［J］.Dynamics of Continuous，Discrete and Impulsive Systems Series A:Mathematical Analysis，2010(17):215 －232.

［5］Lawrence CEvans.A survey of entropy methods for partial differential equations［J］.Bulletin AMS，2004，41(4):409－438.

［6］Walter rudin.Functional analysis:second edition［M］.刘培德，译.北京:机械工业出版社，2004:23－57.

［7］Lin FH.On the Dirichlet problem forminimal graphs in hyperbolic space［J］.Inventiones Mathematica，1989，96(3):592－612.

［8］Daskalopoulos P，Hamilton R.Regularity of the free boundary for the 2 dimensional porousmedium equation［J］.JAmer Math Soc，1998，11(4):899 －965.

［9］Daskalopoulos P，Hamilton R，Lee K.All time c∞regularity of the interface in degenerated diffusion:a geometric approach［J］.Duke Math J，2001，108(2):295－327.