线性缓冲算子及其矩阵表示研究

刘卫锋，何 霞

(郑州航空工业管理学院数理系，河南 郑州 450015)

针对灰色预测建模中存在波动较大数据问题，文献［1］中首度提出了缓冲算子的概念和公理系统，并对缓冲算子的特性进行研究，开启了利用缓冲算子研究波动数据的大门.文献［2－11］在文献［1］的基础上，构造了许多不同的强化缓冲算子和弱化缓冲算子，并对其性质进行了更深入的研究，揭示了一些缓冲算子之间的内在联系.文献［12］构造了一类线性弱化缓冲算子和强化缓冲算子，并从矩阵的角度研究它们的复合运算.本文在上述研究基础上，将文献［12］中涉及的线性缓冲算子概念一般化，并给出严格的数学定义，然后定义了线性缓冲算子矩阵的概念，最后给出了利用线性缓冲算子矩阵对线性缓冲算子类型进行判断的方法.

1 线性缓冲算子及其矩阵表示

定义1 设X1=(x1(1)，x1(2)，…，x1(n))，X2=(x2(1)，x2(2)，…，x2(n))是任意两个非负序列，D是一个缓冲算子，λ是任意非负实数.称D是一个线性缓冲算子，若D满足条件

(1)(X1+X2)D=X1D+X2D;(2)(λX1)D= λ(X1D).

显然，线性缓冲算子本质上就是线性变换.将X1，X2看成具有n个分量的向量，则定义1中的两个条件告诉我们，线性缓冲算子保持向量的加法和数量乘法.

定义2 设 X1=(x1(1)，x1(2)，…，x1(n))，X2=(x2(1)，x2(2)，…，x2(n))是任意两个非负序列，D是一个缓冲算子，λ1，λ2是任意非负实数.称D是一个线性缓冲算子，若D满足条件

(3)(λ1X1+λ2X2)D= λ1(X1D)+λ2(X2D).容易证明，定义1和定义2是等价的.对定义2中的条件(3)作数学归纳法，容易得到

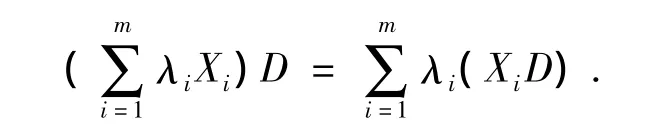
其中 λ1，λ2，…，λm是任意非负实数.

定义3 X=(x(1)，x(2)，…，x(n))是系统行为数据序列，D是一个线性缓冲算子.称D是一个线性弱化缓冲算子，若缓冲序列XD比原始行为数据序列X的增长速度(或衰减速度)减缓或振幅减少.

定义4 X=(x(1)，x(2)，…，x(n))是系统行为数据序列，D是一个线性缓冲算子.称D是一个线性强化缓冲算子，若缓冲序列XD比原始行为数据序列X的增长速度(或衰减速度)增强或振幅增大.

定义5 设 X=(x(1)，x(2)，…，x(n))是系统行为数据序列，D是一个线性缓冲算子，XD=(x(1)d，x(2)d，…，x(n)d)，则 有 XD=(x(1)，x(2)，…，x(n))A .其中 A=(aij)nn，称A为线性缓冲算子D的线性缓冲算子矩阵.

例1 设 X=(x(1)，x(2)，…，x(n))是系统行为数据序列，各时点的权重为ω =(ω1，ω2，…，ωn)，ωn≠0，ωk≥ 0(k=1，2，…，n)，XD1=(x(1)d1，x(2)d1，…，x(n)d1)，其中 x(k)d1)，k=1，2，…，n，则 D1是线性弱化缓冲算子.

证明 设X1=(x1(1)，x1(2)，…，x1(n))，X2=(x2(1)，x2(2)，…，x2(n))是任意两个非负序列.文献［3］中已经证明了D1是弱化缓冲算子.故只需证明D1是一个线性缓冲算子即可.

由定义1可知，D1是一个线性缓冲算子.故D1是一个线性弱化缓冲算子.其线性缓冲算子矩阵为:

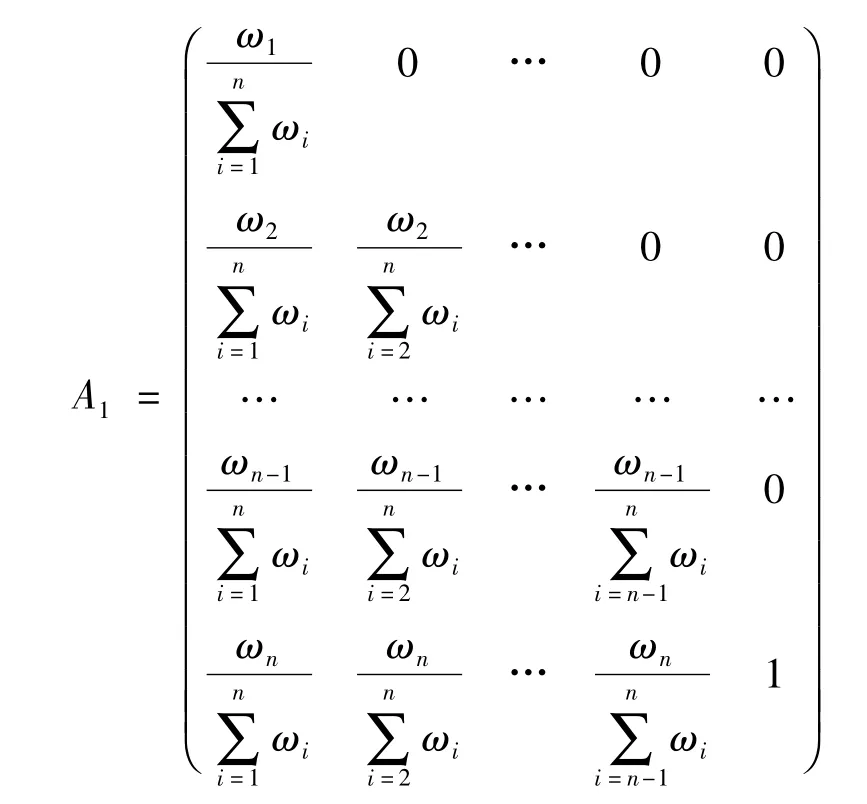
说明:(1)线性缓冲算子矩阵A与线性缓冲算子D的作用完全相同，只是表达形式不同:一个是公式表示，一个为矩阵表示.故本质上它们是一一对应关系.

(2)线性缓冲算子必须满足条件x(n)d=x(n)，故线性缓冲算子矩阵的一个明显特征是，其最后一列元素除ann=1之外，其余全为零.

(3)设原始序列为 X=(x(1)，x(2)，…，x(n))，显然

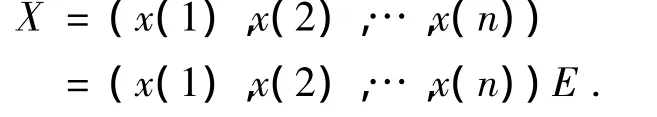
其中E为单位矩阵，即恒等线性算子矩阵为单位矩阵E.

例2 设 X=(x(1)，x(2)，…，x(n))是系统行为数据序列，XD2=(x(1)d2，x(2)d2，…，x(n)d2).其中x(k)，k=1，2，…，n，则 D2是线性弱化缓冲算子.

证明 例1中的ω =(1，…，1)时，线性弱化缓冲算子D2就是D1的特殊情况，故D2是线性弱化缓冲算子.

例3 设 X=(x(1)，x(2)，…，x(n))是系统行为数据序列，XD3=(x(1)d3，x(2)d3，…，x(n)d3)，其中

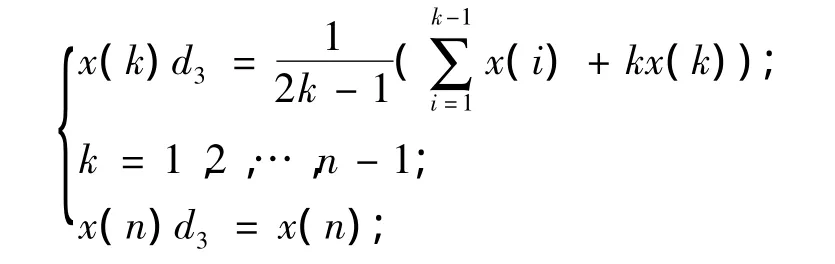
则当X为单调增加序列或单调衰减序列时，D3是线性强化缓冲算子.

证明 文献［1］中已经证明D3是强化缓冲算子，只需再证其是线性缓冲算子即可.

设 X1=(x1(1)，x1(2)，…，x1(n))，X2=(x2(1)，x2(2)，…，x2(n))是任意两个非负序列，则

控制系统使用增量式编码器来获取同步信号，编码器和切刀盘连接，编码器旋转一周，切刀切割一支双倍长烟，选择256线编码器。控制系统采集A向脉冲和Z向脉冲，A相脉冲用于采集点同步和计数，Z向脉冲用于确定采集点在烟支上的位置。每收到一个Z向脉冲，就将A相脉冲值清零。

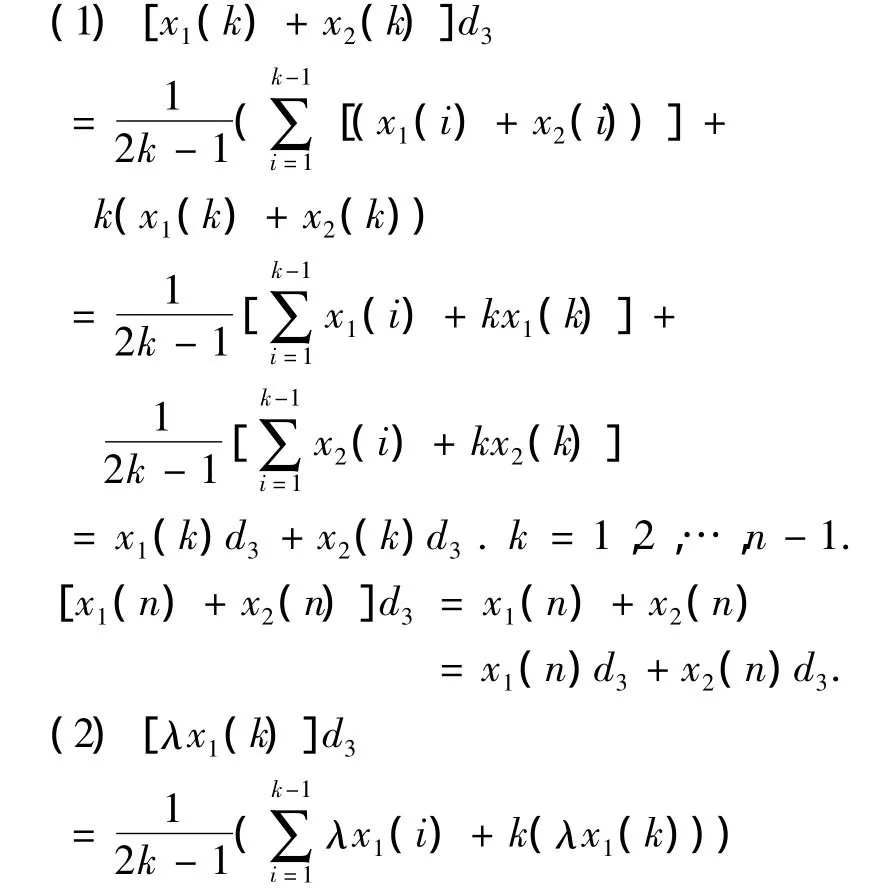
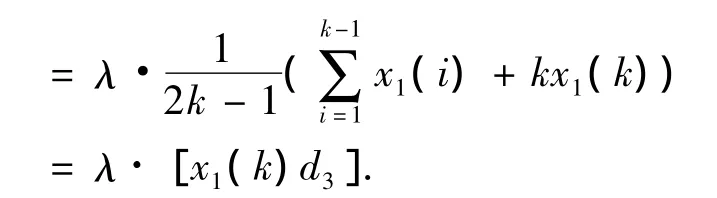
［λx1(n)］d3= λx1(n)= λ·［x1(n)d3］.故D3是线性强化缓冲算子，且其算子矩阵为

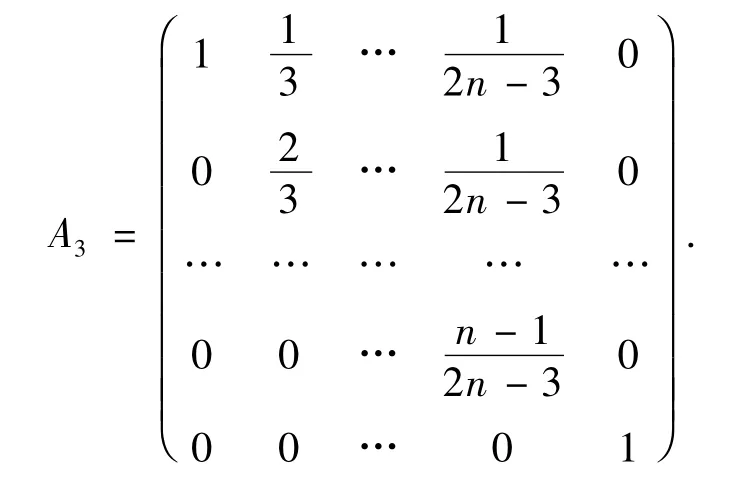
2 线性缓冲算子类型的矩阵判断

由于线性缓冲算子矩阵与线性缓冲算子存在一一对应关系，因此线性缓冲算子是弱化缓冲算子还是强化缓冲算子的判断也可使用线性缓冲算子矩阵来进行.

设 X=(x(1)，x(2)，…，x(n))是非负递增序列，D是一个线性弱化缓冲算子，

XD=(x(1)d，x(2)d，…，x(n)d)=(x(1)，x(2)，…，x(n))A .

因为D是线性弱化缓冲算子，且X是非负递增序列，故有 x(k)d ≥ x(k)，k=1，2，…，n-1，x(n)d=x(n);而x(k)d=)，因此x(k)d≥x(k)等价于+(akk-1)x(k))≥0，k=1，2，…，n-1 .

于是，得到利用线性缓冲算子矩阵判断线性缓冲算子类型的方法:

XD=(x(1)d，x(2)d，…，x(n)d)=(x(1)，x(2)，…，x(n))A.

同理可以得到:

定理2 设X=(x(1)，x(2)，…，x(n))是非负衰减序列，D是一个线性缓冲算子，且XD=(x(1)d，x(2)d，…，x(n)d)=(x(1)，x(2)，…，x(n))A.

是线性缓冲算子矩阵，则:

定理3 设X=(x(1)，x(2)，…，x(n))是非负振荡序列，D是一个线性缓冲算子，且XD=(x(1)d，x(2)d，…，x(n)d)=(x(1)，x(2)，…，x(n))A.

(1)D是线性弱化缓冲算子时的充要条件:.

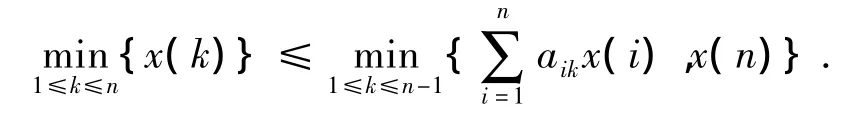
(2)D是线性强化缓冲算子时的充要条件:

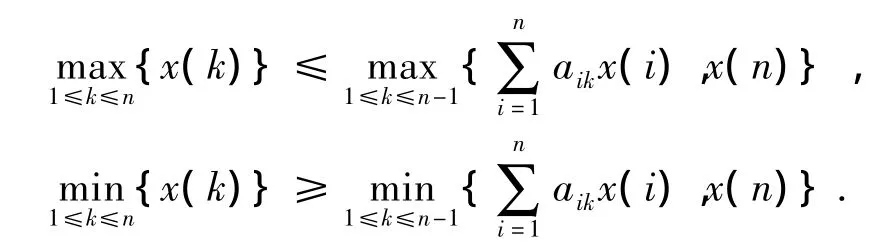
同理可证:

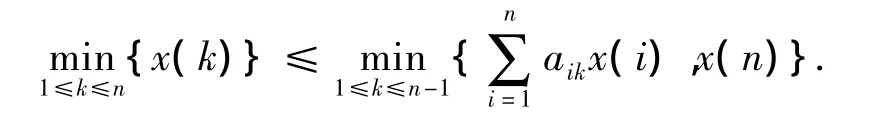
(2)证明同(1)类似.

例4 设X=(1，1.5，2.5，3)是系统行为数据序列，D2是一个线性缓冲算子，其中x(k)d2=(i)，k=1，2，…，n，则 XD2=(1，1.5，2.5，3)A2，其中

3 结论

文章在定义线性缓冲算子及线性缓冲算子矩阵的基础上，给出了利用线性缓冲算子矩阵来判断线性缓冲算子类型的方法，从而打开了利用矩阵来研究线性缓冲算子的大门，并为如何利用矩阵方法构造更多的线性缓冲算子以及利用矩阵运算表示线性缓冲算子的复合运算奠定了数学基础，同时对利用矩阵方法研究非线性缓冲算子性质和构造也有一定的启发意义.

［1］刘思峰.冲击扰动系统预测陷阱与缓冲算子［J］.华中理工大学学报，1997，25(1):25 －27.

［2］谢乃明，刘思峰.一种新的实用弱化缓冲算子［J］.中国管理科学，2003，11(S):46 －48.

［3］党耀国，刘思峰，刘斌，等.关于弱化缓冲算子的研究［J］.中国管理科学，2004，12(2):108 －111.

［4］党耀国，刘斌，关叶青.关于强化缓冲算子的研究［J］.控制与决策，2005，20(12):1332 －1336.

［5］谢乃明，刘思峰.强化缓冲算子的性质与若干实用强化算子的构造［J］.统计与决策，2006(4):9－10.

［6］关叶青，刘思峰.关于弱化缓冲算子序列的研究［J］.中国管理科学，2007，15(4):89 －92.

［7］党耀国，刘思峰，米传民.强化缓冲算子性质的研究［J］.控制与决策，2007，22(7):730 －734.

［8］关叶青，刘思峰.强化缓冲算子序列与m阶算子作用研究［J］.云南师范大学学报，2007，27(1):32 －35.

［9］崔杰，党耀国.一类新的弱化缓冲算子的构造及其应用［J］.控制与决策，2008，23(7):741 －744.

［10］吴正朋，刘思峰，米传民，等.弱化缓冲算子性质研究［J］.控制与决策，2010，25(6):958 －960.

［11］魏勇，孔新海.几类强弱缓冲算子的构造方法及其内在联系［J］.控制与决策，2010，25(2):196 －202.

［12］关叶青，刘思峰.线性缓冲算子矩阵及其应用研究［J］.高校应用数学学报，2008，23(3):357 －362.