基于SODM的支持向量机的多分类器融合算法

宋 磊

（济南大学管理学院，济南 250022）

0 引言

支持向量机SVM（Support Vector Machines）是学者Vapnik提出的结构化风险最小的统计学习理论[1～3]，主要研究小样本情况下的统计学习方法，是目前国际上最为流行的机器学习和模式识别技术，并在很多领域成功应用。但是，随着企业信息化水平的逐步推进，需要处理的数据急剧增加，而一般的支持向量机技术在挖掘和分析海量的数据时，内存开销大、训练速度慢的缺点极大阻碍了支持向量机方法的应用。因此。许多学者对传统支持向量机提出许多改进。

一类方法是改进支持向量机的训练方法，如：Platt[4,5]，Keerthi等[6]提出了基于序列最小优化（SMO，Sequence Minimal Optimization），将大的二次规划分解为一系列小的二次规划，使得SVM处理大样本数据的速度大大提高；Lee等[7]提出随机选取子集的减少样本训练量的方法（RSVM，Reduce Support Vector Machine）；Zhang[8]提出了递归支持向量机方法（R-SVM，Recursive Support Vector Machine）去除噪声点以降低计算强度。刘向东[9]和秦玉平[10]提出FCSVM（Fast Classification Support Vector Machine）采用二分法优化分类函数中的支持向量数。

另外一类方法是改进样本处理方法，如：Schölkopf等[11]提出了将大样本分成不同的子样本的方法；。Osuna[12]提出的工作集算法（Working Set）；Domeniconi等[13]提出多支持向量机分类器的并行学习算法；Collobert[14]提出w-model算法，使用多个支持向量机分类器的组合来解决大样本分类问题；。Lin[15]也提出了加权的模糊支持向量机（FSVM）。

本文也是采用多分类模型（MSVMs，Multiple Support Vector Machine）的方法改进样本处理速度，考虑到采用不同的分类模型的分类结果有较大差异，且具有互补性，将不同分类器分类结果进行融合，得到综合分类结果可以发挥各个分类模型在各自空间的分类优势。但目前的多分类器技术大多采用Borda计数、贝叶斯方法等，分类时可能产生一些冗余和冲突。因而，多分类器的选择性融合是最佳选择。Ivakhnenko[16]提出的自组织数据挖掘理论（SODM，Self-Organize Data Mining）构造一个多层前馈神经元网络结构，通过遗传，进化，变异，选择和淘汰等一系列操作，来决定系统模型的输入变量，结构以及参数，最后通过终止法则来选择最优复杂度模型[17]。本文将利用自组织数据挖掘SODM，将其应用于支持向量机多分类器分类算法的优化，解决多分类器产生一些冗余和冲突。

1 支持向量机多分类器融合

1.1 基于one-against-all策略的支持向量机的多分类器

支持向量机的多分类器是由两分类支持向量机扩展来解决多分类问题，通过合并多个两分类SVM分类器来构造MSVM的三类典型方法，即one-against-all，one-against-one，DAGSVM方法。

one-against-all方法是对k类问题构造k个分类器，第i个SVM用第i类中的训练样本作为正的训练样本，将其他的样本作为负的训练样本。

首先，建立k个两分类SVM分类器。第i个SVM把第i类与其他类分隔开，i=1,2,…,k（第i类样本的类属性设为1，其他样本的属性设为-1），第i个支持向量机解决以下的优化问题：

其中，C为罚因子，是允许xj被错分的松弛因子，通过求解上式，可以得到k个距离函数：

最终输出的是于具有最大值的距离函数的类：

1.2 w-model多分类器融合算法

2 自组织选择性融合多支持向量机算法

2.1 自组织数据挖掘理论

自组织数据挖掘（SODM，Self-Organize Data Mining）的基本思想是构造一个多层前馈神经元网络结构，从参考函数出发，通过遗传，进化，变异，选择和淘汰等一系列操作，来决定系统模型的输入变量结构以及参数，最后通过终止法则来选择最优复杂度模型。SODM的核心技术是GMDH（Group Method of Data Handling）算法，GMDH算法将观测样本数据分为训练集(training set)和测试集(testing set)，建立因变量(系统输出)和自变量(系统输出)之间的一般函数关系，一般常用K-G（Komogorov-Gabor）多项式：

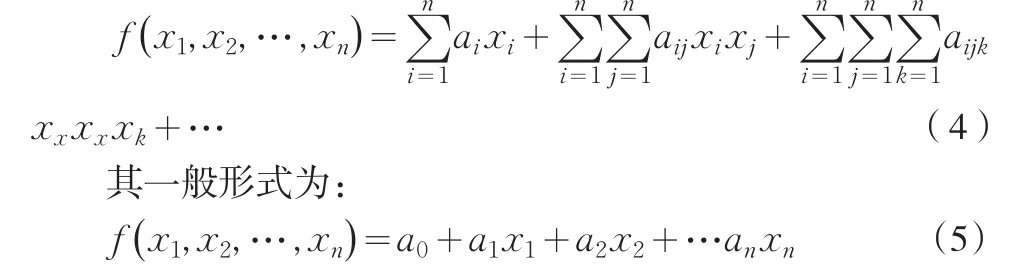
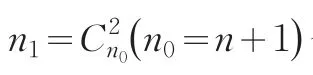
，，是训练集上利用最小二乘(LS)估计得到的参数，通过阈值度量，F1(≤n1)个局部函数（F1称为选择自由度)被选出，并再次以两两配对的形式作为第2层的输入：

不断重复以上过程，直到满足中止法则，得到最优复杂度模型时停止。

中止法则是：当模型的复杂度逐渐增加时，具有“外补充”性质的选择准则(外准则)中选出一个作目标函数，外准则的准则值会呈现先减小后增大的变化趋势，外准则全局极小值对应了最优复杂度模型[17]。

在多分类器融合中，融合方案的优劣最直接的测度指标就是其融合后的分类误差，根据贺昌政[21]选择外准则为：

(B)表示测试集B上建立的模型对应训练集A中的预测值，(A)表示测试集A上建立的模型对应训练集B中的预测值。

2.2 选择性融合多支持向量机

假设现在有k个分类器：Ψ(1)，Ψ(2)，…，Ψ(k)，每一个分类器属于分类：i=M{1 ,2,…,M}，这样，大样本集的SVM问题就变成一系列小的二次规划问题（QP）。

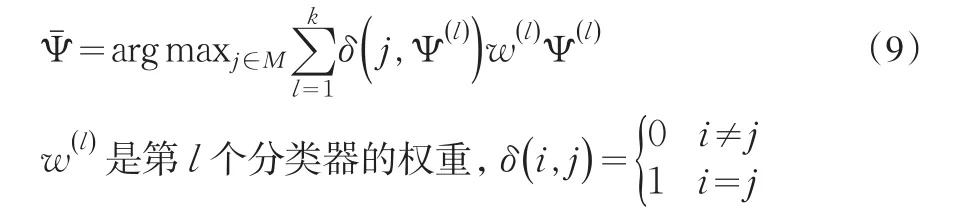
现在我们分析三个分类器的支持向量机分类问题。由于自适应线性神经元（Adaline）的数量m1对GMDH网络的影响很大，当层数增加时，GMDH网络的中与预测无关的值会大量增加，并直接影响预测分类预测的精度。按照PPS准则（prediction sum of squared）和AIC准则（Akaike Information Criterion）.（Tamura，1978）[22]，自适应线性神经元（Adaline）定义为：

其中，是残差平方和，是估计值，C是和m相关的一个常量。

假设在[0 ,TLC]时间内，累积性错误被记为随机计数过程{N(t),t＞0} ，那么，发生在[0 ,TLC]间的错误总期望V(TLC)为：

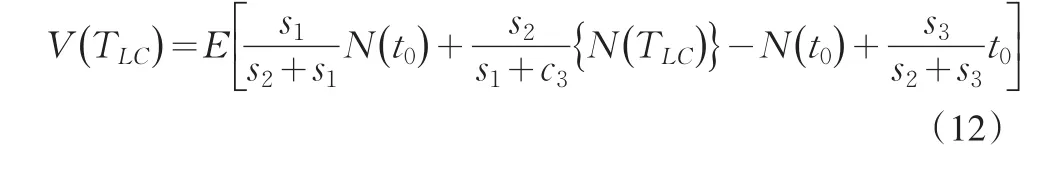
s1，s2，s3分别为三个分类器的累积性错误标准差。那么，取得min{V(TLC) }的TLC即是运算终止时间，此时对应的分类即为最终的分类结果。

3 仿真实验

J.A.Mueller和L.Frank开发了功能强大的自组织数据挖掘软件包KnowledgeMiner，使SODM成功地应用于各个领域的建模实践。本例采用台湾信用卡数据，32个字段，1301068条记录，利用KnowledgeMiner软件，分别随机抽取10%，20%，…，100%，SVM分类器分别选取，高斯核RBF分类器、d维多项式分类器、多层感知器分类器三种，对比单独使用这三种分类器、w-model多分类器融合算法和本文的自组织选择性融合多分类器算法（SOSF）的预测精度如表1。

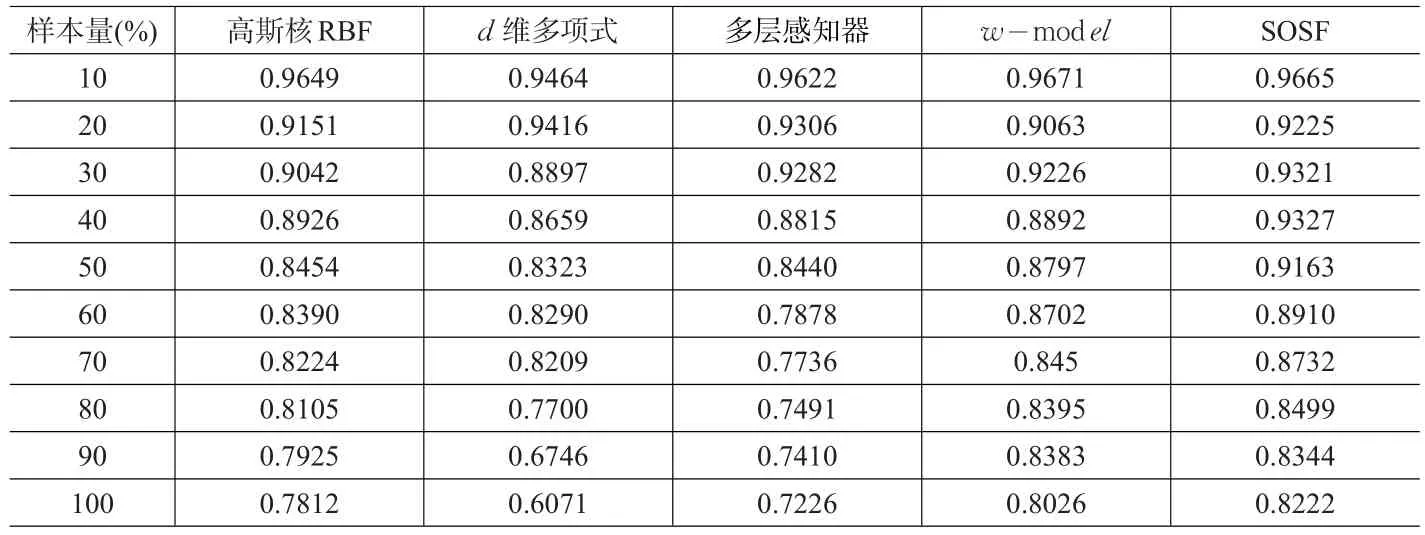
表1 10个数据集上的分类精度比较（%）

4 结论

将自组织数据挖掘理论引入支持向量机多分类器融合的学习中，实现选择性多分类器融合，PPS准则和AIC准则，以累积性错误总期望V(TLC)最小为分类终止条件，有效解决大样本多分类器融合受子样本分布状态影响、各分类器学习能力相差过大的缺点，从而提高了训练效率和分类效率。在本文的信用卡数据实验中发现，在样本量较小的情况下单一分类器分类误差和多分类器分类误差差别不大，而随着样本容量的逐步增大，多分类器分类误差有明显提高，特别是本文的自组织选择性融合多分类器算法（SOSF）优于w-model多分类器融合算法。

[1]Vapnik V,Lerner A.Pattern Recognition Using Generalized Portrait Method[J].Automation and Remote Control,1963,24(6).

[2]Vapnik V.The Nature of Statistical Learning[M].New York:Springer,1995.

[3]Vapnik V.Theory of Support Vector Machines[D].Royal Holloway;University of London,1996.

[4]Platt J.Sequential Minimal Optimization:A Fast Algorithm for Training Support Vector Machines[J].Advances in Kernel Methods Support Vector Learning,1998,208.

[5]Platt J C.Fast Training of Support Vector Machines Using Sequential Minimal Optimization[C].MIT Press,1999.

[6]Keerthi S S,Shevade S K,Bhattacharyyc C,et al.Improvements to Platt's SMO Algorithm for SVM Classifier Design[J].Neural Computation,2001,13(3).

[7]Lee y J,Mangasarian O L.Rsvm:Reduced Support Vector Machines[R].Wisconsin:Data Mining Institute,Computer Sciences Department,University of Wisconsin,2000.

[8]Zhang x,Lu x,Shi Q,et al.Recursive SVM Feature Selection and Sample Classification for Mass-spectrometry and Microarray Data[J].BMC Bioinformatics,2006,7(1).

[9]刘向东,陈兆乾.一种快速支持向量机分类算法的研究[J].计算机研究与发展,2004,41(8).

[10]秦玉平,王秀坤.一种改进的快速支持向量机分类算法研究[J].大连理工大学学报,2007,47(2).

[11]Sch Lkopf B,Chris Burges,Vapnik V.Extracting Support Data for a Given Task;Proceedings of the First International Conference on Knowledge Discovery and Data Mining,Menlo Park,Canada[C].AAAI Press,1995.

[12]Osuna E,Freund R,Girosi F.Improved Training Algorithm for Support Vector Machines;Proceedings of the Procedings of the Ieee Nnsp[C].Amelia Island,1997.

[13]DomeniconI C,Gunopulos D.Incremental Support Vector Machine Construction;Proceedings of the In Proceedings of of International Conference on Data Mining,Califomia,USA[C].IEEE,2002.

[14]Collobert R,Bengio S,Bengio Y.A Parallel Mixture of Svms for very Large Scale Problems[J].Neural Computation,2002,14(5).

[15]Lin C F.Fuzzy Support Vector Machines[J].Neural Networks,IEEE Transactions on Neural Networks,2002,13(2).

[16]Ivakhnenko A G.Heuristic Self-organization in Problems of Engineering Cybernetics[J].Automatica,1970,6(2).

[17]Mueller J A,Lemke F.Self-organising Data Mining:An Intelligent Approach To Extract Knowledge From Data[M].Hamburg:Libri,1999.

[18]Yan W W,Chen Z G,Shao H H.Multi Support Vector Machines Decision Model and its Application[J].Journal of Shanghai Jiaotong University(Science),2002,7(2).

[19]Platt J C,Cristianini N,Shawe-taylor J.Large Margin DAGs for Multiclass Classification.Advances in Neural Information Processing Systems[M].Cambridge,MA:MIT Press,2000.

[20]Anastasio P L,Pan h,Liang Z,et al.A Hybrid Nn-Bayesian Architecture For Information Fusion;Proceedings of the Proceedings of ICIP98[C].Citeseer,1998.

[21]贺昌政.自组织数据挖掘与经济预测[M].北京:科学出版社,2005.

[22]Tamura H,Kondo T.Revised GMDH Algorithm Using Prediction Sum of Squared(PSS)as a Criterion for Models Selection[J].Trans Instrument and Control Engineering,1978,（14）.