相关四格表数据资料检验方法的进展与应用

陆运清

（河北师范大学 教育学院，石家庄 050024）

1 McNemar检验及其存在的问题

1.1 McNemar检验

两个相关二分变量的差异显著性检验在实际研究中经常涉及，最典型的是前后测实验设计研究。例如，在医学研究中，考查患者服用某种药物或接受某种处理前后是否出现某种症状，以研究该种药物或该种处理对此症状的治疗效果；在营销研究中，调查消费者在看到某产品广告前后购买该产品的情况，以确定该产品广告的效果；在教育研究中，测查学生在接受某教育过程前后某项素质的达标情况，以了解该教育过程的成效；等等。在前后测实验设计中（见表1），a、d分别表示处理前后的测试结果均为“是”和均为“否”的被试数，二者所代表的被试，处理前后测试结果相同。b、c分别表示处理前后测试结果由“是”变为“否”和由“否”变为“是”的部分，二者所代表的被试，处理前后测试结果均发生变化。

对相关二分变量进行统计检验的常用方法是McNemar检验，它是由美国统计学家Quinn McNemar于1947年提出的[1]。McNemar检验的基本公式为

其应用条件为b+c≥10。该卡方分布的自由度为1。

1.2 McNemar检验存在的问题

计数数据资料的检验看似简单，但在实际应用中经常出现误用问题[2][3]。McNemar检验的问题有所不同，是理论上有些不尽如人意。从McNemar检验公式可以看出，只有表示前后测结果不一致的两部分b和c包括在公式中，而处理前后测试结果不发生变化的部分a和d并未包括在其中。Cochran WG于1950年论及前后测结果一致的部分在差异检验中不起作用，并提出这一点不符合直观感觉[4]。对于给定的b和c,直觉应该是前后测试结果差异在a和d为零时要比a和d很大时显著。这一点通过实例更容易理解。例如，将未通过某次标准化考试的学生随机分配到两辅导班培训，培训一段儿时间后这些学生又参加了第二次的标准化考试，如果要考查甲、乙两个辅导班的效果，随机抽取学生了解考试情况，结果抽取的参加甲辅导班的10名学生全部通过考试（a1=0,b1=0,c1=10,d1=0），抽取的参加乙辅导班的30名学生中10名通过了考试(a2=0,b2=0,c2=10,d2=20)。通过McNemar检验考查两个辅导班辅导的效果，二者的检验结果均为χ2=(b-c)2/(b+c)=10,p=0.0015。而具体分析，甲辅导班的效果应该好于乙班。可见，McNemar检验中只存在两次测试不一致的部分具有一定的不合理性。表1相关四格表“前-后测实验设计”示意表

2 与McNemar检验有关的一些推导和分析

2.1 在样本整体基础上推导出McNemar检验的方法存在的问题

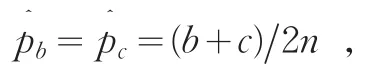
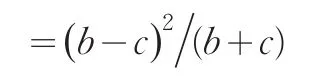
因此，研究者得出了McNemar检验公式。实际上，这个推导过程对a和d的极大似然估计并没有意义，这种估计方法a和d永远不起作用。退一步讲，即使承认该推导过程，得出的检验公式也只是计算卡方的公式形式上与McNemar检验公式相同，而实际上并不能像文中论及的一样：该过程得出McNemar检验。因为McNemar检验的卡方分布的自由度为1，而此推导过程的分类项数为4（与McNemar的推导过程相比，差别仅是多出了关于a和d的两项），因此，该卡方分布的自由度为3。这样，这个推导过程并不能得出McNemar检验，更不可能正确解释McNemar检验中不包含a和d的问题。

2.2 目的不同的两种检验

统计学家还就比之比、对数比、风险比等其它一些方法作过相关四格表差异显著性检验的研究，但这些方法均为得出更合理的结果[7]。

3 McNemar检验的修正公式和几个研究结果的修正

3.1 McNemar检验的合理修正

通过重新组合分组的方法，研究者简单巧妙地解决了在样本整体基础上考虑两个变化项一致的问题[8]。将样本n考虑成b和a+c+d或者c和a+b+d两个分项，则对应两项的理论次数分别为（b+c）/2和n-(b+c)/2,这个过程既考虑到整个样本，又使得b和c对应的理论次数相等。在此基础上用Pearson卡方和二项分布近似的正态分布均可以推导出相关四格表数据的检验公式[8]

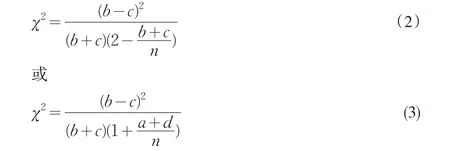
在b+c≥10时，公式（2）和（3）的计算结果符合自由度为1的卡方分布。这个结果对McNemar检验进行了合理修正。

用修正公式（2）和（3）对本文开始部分的甲、乙辅导班的效果进行检验，则甲辅导班的效果检验结果χ2=10，p=0.0015；乙辅导班的检验结果χ2=5.36，p=0.0206。甲辅导班的效果更显著。

修正后的McNemar检验不但依赖于前后测验结果发生变化的被试数目b和c，还与总样本容量n或前后测验结果不变的被试的数目a和d有关。在b和c一定的情况下，修正后的卡方值随着a和d的增大而减小，当a+d=0时，与修正前的值相等。这个结果更具有合理性。

3.2 几个研究结果的修正

由于McNemar检验仅考虑两次测试有变化的部分b和c，因此检验结果扩大了具有统计学意义的可能性。在此抽取几个采用了McNemar检验的研究文献，将其研究数据用McNemar检验的修正公式重新进行检验，两种检验的有关结果如表2。

从表2中的数据可以看出，修正公式检验结果相对于McNemar检验结果的显著性在不同程度上降低了。其中数据⑵⑶⑺⑻⒀⒂⒃McNemar检验结果为p＜0.05,修正公式的检验结果为p＞0.05；数据⑷⑸⑹⑽⑾⑿的McNemar检验结果为P＜0.01,修正公式的检验结果为p＜0.05；数据⑴、⑼、⒁的McNemar检验结果分别为p＜0.01,p＜0.001,p＜0.001，修正公式的检验结果分别为p＞0.05,p＜0.01,p＜0.05。由于McNemar检验只考虑两次测试结果的不一致部分b和c,将两次测试结果的差异放大，因此，造成I型错误的显示值比真实值小，有时使差异本不显著的数据检验结果显示为显著。修正后的检验结果修正了这个误差。例如，文献[6]中甲、乙两种方法检验细菌的结果差异未达到显著水平，但McNemar检验结果差异非常显著。文献[9]中的McNemar检验结果显示，腰围指数和腹部肥胖诊断代谢综合征的结果差异显著，修正检验得出两种诊断结果的差异不显著。文献[10]中的McNemar检验结果显示，新生儿血清HBV-DNA阳性组PBMC中HBV-DNA检出率明显高于血清HBV-DNA阴性组，而修正检验结果显示，阳性组与阴性组的检出率差异不显著。文献[13]中，在对自闭症谱系障碍分析中，被试回答有关自闭症测试的两种问题通过率的McNemar检验结果为差异显著，而修正后的检验结果未达到显著程度；对TD(typically developing）组的分析中，两种问题测试通过率的差异检验结果也如此。文献[15]中通过基本护理筛查(ADS-PC)和简明精神量表（MMSE）对不同组别老年痴呆病人组和非痴呆病人组测试结果进行检验，原文表3中第5组的白人及表4中第6组的受教育年限大于12年的被试的测试结果而言，McNemar检验结果显著，而修正结果显示二者差异不显著。文献[16]对选修家庭暴力问题课程的同学在上课前后调查其是否遭到过家庭暴力，结果显示，上课后回答曾经遭受家庭暴力的学生增多，McNemar检验差异显著，但修正检验的结果差异不显著。修正后的检验纠正了因仅考虑变化部分而放大了差异性的问题。

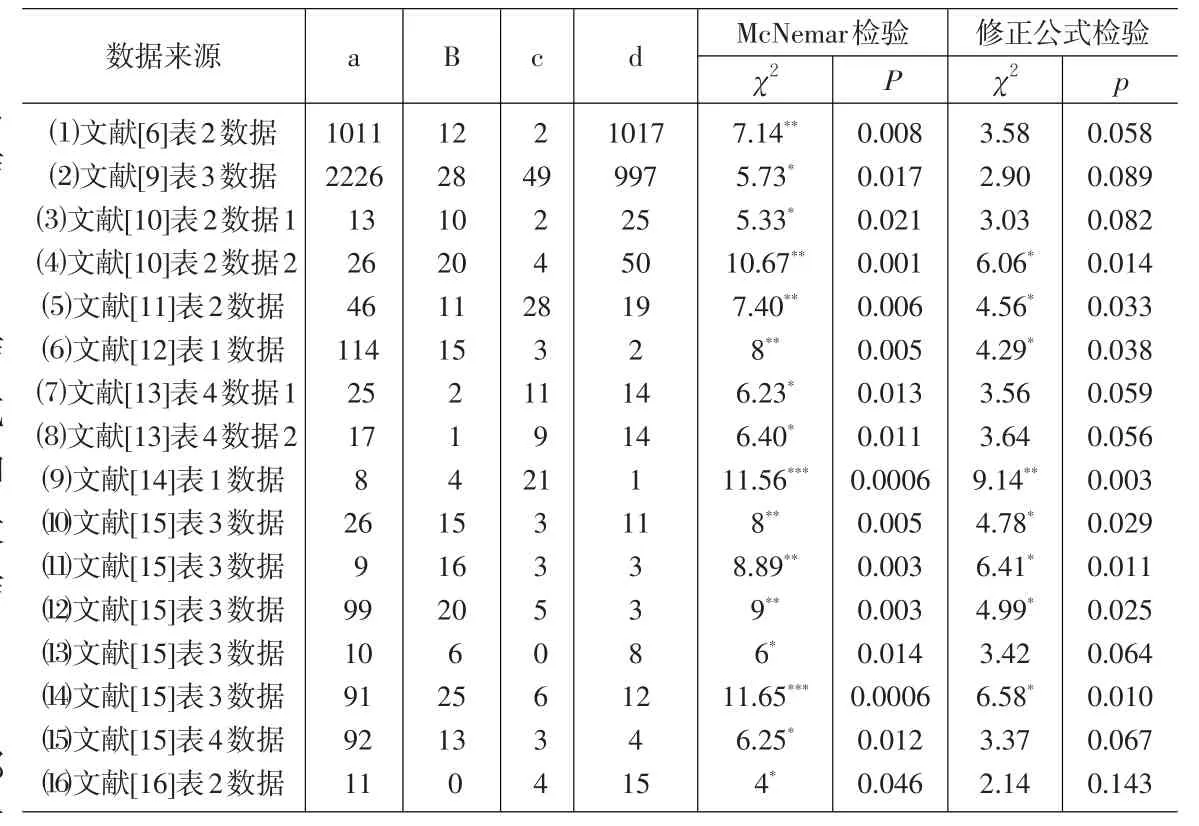
表2 几个研究文献中数据的两种检验结果

4 结语

相关二分变量的统计处理除在前后测设计中广泛应用外，对配对研究设计中的数据分析也适合。如双胞胎对两种性质活动的选择是否有相同偏好；夫妻对某项社会决策的赞成和反对意见是否一致；父子对两种养老方式的赞成倾向是否相同；等。可见，相关二分变量在很多领域的实际研究中应用相当普遍。因此，选用合适的统计方法对相关二分变量进行分析以得出更科学的研究结果，为生活、工作实际提供更为有效的指导是非常必要的。

[1]McNemar Q.Note on the Sampling Error of the Difference between Correlated Proportions or Percentages[J].Psychometrika，1947,（12）.

[2]陆运清.用Pearson’s卡方统计量进行统计检验时需要注意的几个问题[J].统计与决策，2009,(15).

[3]陆运清.心理与教育研究中列联表统计检验的几种常见错误辨析[J].统计与决策，2010,(15).

[4]Cochran WG.The Comparison of Percentages in Matched Samples[J].Biometrika,1950,(37).

[5]罗明奎.配对资料McNemar检验法的适用范围[J].中国卫生统计，1999,16(3).

[6]赵莹.配对四格表的一致性检验[J].数理医药学，2010,23(4).

[7]Agresti A，Min Y.Effects and Non-Effects of Paired Identical Observations in Comparing Proportions with Binary Matched-pairs Data[J].Statistics in Medicine,2004,(23).

[8]Yunqing Lu.A Revised Version of McNemar’s Test for Paired Binary Data[J].Communication in Statistics-Theory and Methods,2010,39(19）.