风暴潮灾害综合财产险精算定价模型探析

赵 昕，王晓婷

（中国海洋大学，山东青岛 266100）

0 引言

中国海岸线漫长，南北跨度较大，且面临台风多发的太平洋洋面，每年会遭受多次台风风暴潮。同时由于沿海城市多是我国经济发达省份，风暴潮往往给沿海城市及居民等造成巨大经济损失，对我国灾害管理体系提出巨大考验与挑战。目前我国在自然灾害管理过程中具有典型的政府主体性、资金配置财政性、管理方式计划性等特点。这种风险管理机制固然有其自身的优越性，例如国家对救灾资源调动较为迅速和集中等。但相对而言，政府面临巨大的财政压力，且仅依靠社会救助无法满足灾害损失的补偿。面对风暴潮灾害频发的现状，迫切需要依托经济市场的手段解决自然灾害所带来的损失，风暴潮灾害保险成为应对风暴潮灾害的首要选择。

风暴潮灾害保险没有成立主要是由于我国保险市场发展不完善，但更重要的是风暴潮灾害一直被视为一种巨灾保险，单纯依靠市场化保险公司无法承担如此巨大风险。但从风暴潮灾害常造成的巨大损失来看似乎如此，但与地震等自然灾害不同的是，由于风暴潮灾害的多发性，其造成大额损失的概率极低，并且每次损失的地理分布也不集中，并不符合巨灾的特点。本文拟从风暴潮损失的分布拟合入手，判别风暴潮损失的损失特征，并讨论风暴潮灾害保险建立的可行性，进而依据保险精算理论对风暴潮灾害保险进行定价研究，从而探讨风暴潮灾害保险的现实可行性，为相关部门提供对策建议。

1 风暴潮灾害损失特征分析

在风暴潮灾害保险进行定价时，首先需要确定风暴潮灾害保险的损失特征，即此种自然灾害保险是否具有右尾特征，也就是说是否属于巨灾保险，进而确定是否需要对保险分布的尾部进行处理，从而选择适合的保险精算方法进行保险定价。传统保险一般认为风暴潮灾害属于巨灾风险，但一直未给出相关证明，本文从损失分布拟合的角度探寻风暴潮灾害保险的损失分布特点，以确定风暴潮灾害保险的尾部特征是否真正属于巨灾风险的范畴，为后文风暴潮灾害保险定价提供依据。

损失分布理论主要研究在以致发生某一损失的条件下，相应损失量的分布情况。其主要目的是确定风险的严重程度以便管理。分布拟合要解决三个主要问题：

第一是要判断所研究的数据来自哪一种分布模型；

第二是确定分布中的未知参数。也就是在假设数据来自某类分布模型时，如何确定其中的未知参数；

第三是指出拟合的效果，通常通过统计显著性检验来完成。

1.1 损失分布的拟合

第一步，根据经验分布[1]以及经验剩余期望函数[2]形状选择合适的分布模型，主要有帕累托分布、伽马分布、威布尔分布、指数分布、正态分布等。

1.1.1 经验分布

经验分布就是累计频率，设有样本X1,…,Xn，及x轴的分割点c0＜c1＜c2＜…＜ck-1＜ck，且一般有：c0≤min(xi)，ck≥max(xi)，cj(j=1,2…,k-1)不与任何样本xi重合。分割点c0＜c1＜c2＜…＜ck-1＜ck不要求等距离，但必须使连接[c0,Fn(c0)=0]，[c1,Fn(c1)]，…[ck-1,Fn(ck-1)],[ck,Fn(ck)]等点的折线较好地拟合经验分布函数Fn(x)。

Fn(x)是x的跳跃增函数，在每个无重复值xi处跳跃1n，0≤Fn(x)≤1。当x1,…,xn互不相等时，把这n个值按从小到大的顺序排列，记为x(1)＜x(2)＜…＜x(n)，则

当X1,…,Xn是某总体X～F(x)的独立同分布的样本时，统计学上可以证明Fn(x)依概率收敛到F(x)，所以当n比较大时，可以用Fn(x)近似代替F(x)。

1.1.2 经验密度函数

对于分组数据，按照前面的定义构造经验分布函数是不可能的。但是仍然能够估计函数的分布情况。定义分组数据的经验密度函数为

其中，nj为区间[cj-1,cj)内函数值的频数。

由此得到的图形称为直方图，这种方法的最大优点在于，直方图代表了密度函数，并且直方图下方图形的面积可以用来得到经验概率值。

1.1.3 剩余期望函数

由于非寿险中常考虑巨灾损失引起的准备金、再保险安排等问题，损失分布的尾部常常受到特别关注，常常只考虑一定金额值以上的期望值，即用尾部期望函数也就是剩余期望函数来描述它。

设X是一个随机变量，密度函数为f(x)，分布函数为F(x)，对给定的实数d，定义剩余期望函数为

e[X;d]表示随机变量X比d的高出值的平均水平，也就是在X≥d的条件下求X-d的期望值。如果X表示产品的使用寿命，则e[X;d]就表示产品使用时间d后剩余的平均寿命。因此e[X;d]反映的是随机变量尾部的性质，是对随机变量做了“掐头”的处理。剩余期望函数e[X;d]的增减性与分布的具体形式有关，这条性质对分布拟合中选择模型很有帮助。

以下介绍由样本值计算经验剩余期望函数值的方法，根据总体剩余期望函数的计算公式，得经验剩余期望函数的计算公式为

当xi互不相等时，顺序统计量x(1)＜x(2)＜…＜x(n)，上式在d=x(k)的值为

第二步，对选用的分布中的参数做出初步估计，一般采用矩估计法或百分位数法等。如果原始数据数目较多，可以考虑采用分组数据进行简化计算。另外也可以运用相关软件对参数进行精确估计，例如极大似然估计法、最小距离法、最小Χ2法等，不过这些方法都有其适用范围，应该视具体情况而定。

第三步，检验损失分布拟合。对未分组数据可以采用剩余期望函数值比较法，对于分组数据可以对损失分布进行拟合优度检验。

1.2 风暴潮损失特征的判别

中国是全球少数几个同时受台风风暴潮和温带风暴潮危害的国家之一，风暴潮灾一年四季、从南到北均可发生，风暴潮灾害每年给我国带来巨大损失。下文根据国家公布的风暴潮灾害损失数据，采用自2000年以来连续54次风暴潮灾害的直接经济损失数据对其分布进行拟合。值得说明的是，风暴潮灾害的直接经济损失数据包含了众多标的物的损失，包括渔船保险、船东保险这普遍意义上的渔业互助险所承保的损失，同时包括了被保险界认为是不可保的海水养殖等在内的其他标的物损失。总之，风暴潮灾害直接经济损失数据属于风暴潮灾害综合保险的经验损失数据，给我们提供了一种用综合保险来补偿风暴潮损失的新的保险保障思路。

首先对发生的54次致灾风暴潮损失数据进行去通胀处理，以使不同年份数据之间具有可比性。并将数据从小到大排列如表1。

根据公式（1）及（4）计算经验分布和经验剩余期望。运用SPSS 软件绘制出二者的散点图（图1、图2），通过二者的散点图可以较好地选择适合的分布模型[3],[4]。

表1 处理后的风暴潮损失数据

图1 损失分布的散点图

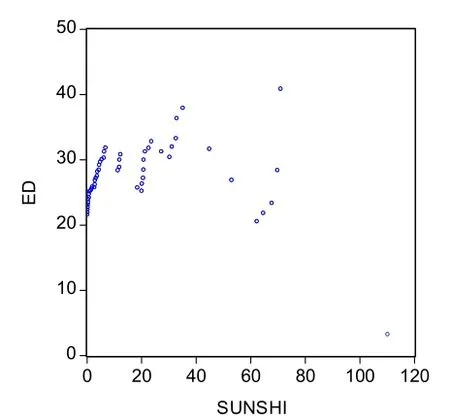
图2 经验剩余期望散点图

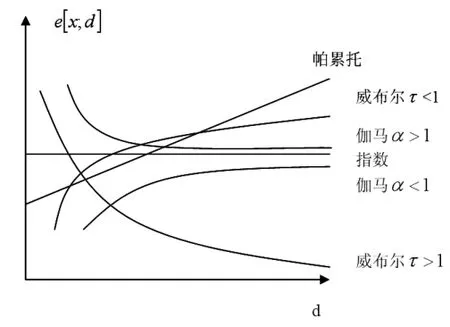
图3 各分布的剩余期望函数曲线

通过比较两幅散点图可以看出，累计概率的尾部趋向平坦，密度概率呈下降趋势。由图2风暴潮损失数据的剩余期望可以看出，尾部并没有表现出明显的变化趋势，很难看出同图3中常见分布函数的剩余期望函数曲线相似，或许表明风暴潮损失分布不具有厚尾特征。因此可以考虑采用密度函数对风暴潮损失数据进行进一步分析。

将初始数据按照Sturges提出的经验公式（5）确定组数，并根据实际情况采取非等距型将数据分成下列6组：(0,1]、(1,10]、(10,30]、(30,50]、(50,100]、(100,114]。得到其概率分布为

K=1+lgnlg2 （5）

通过图4可以看出其概率分布符合保险精算常用分布中的对数正态分布趋势，因此根据对数正态分布进行拟合。运用1stOpt1.0软件，采用牛顿迭代法经过11次迭代，所得拟合结果为

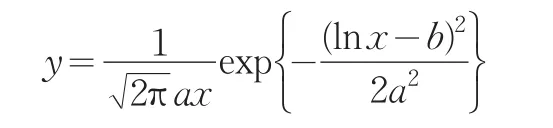
其中，a=5.9123，b=-5.4594，R2=0.9979，曲线拟合图如图5。

进而对对数正态拟合函数进行参数检验，χ2=0.001798，F=1873.7779，顺利通过拟合优度检验，由此可以判断对数正态分布是风暴潮损失分布的有效拟合曲线。

通过上文对风暴潮灾害损失分布的拟合分析可知，潮灾害损失分布属于对数正态分布，由对数正态分布的矩存在性可以看出其尾部较轻，不符合巨灾风险所常有的右尾特征，因此风暴潮灾害风险不属于巨灾风险，可以用一般非寿险精算方法对其进行定价研究。

图4 频率分布直方图

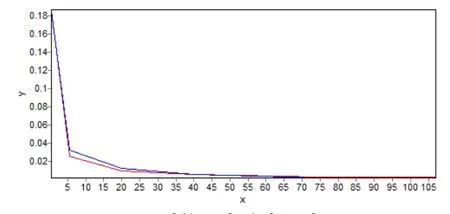
图5 对数正态分布拟合图

2 风暴潮灾害保险的定价

通过上文的研究发现，风暴潮灾害损失分布的有效分布为对数正态分布。对数正态分布是财产险的常用分布之一，根据其矩存在性可以推出对数正态分布的尾部较轻，不属于巨灾风险分布的范畴[5]，可以采用一般非寿险精算方法对其进行定价研究。由于风暴潮灾害保险仅属于理论研究阶段，未投入实际应用，其附加风险保费无法确定。因此，本文主要对风暴潮灾害保险的纯保费进行定价研究。

根据非寿险精算理论相关结论，理论纯保费根据其平均赔款额确定，设赔偿金额Y是一个随机变量，它是另一个随机变量——损失金额X的总数，即Y=f(x)，设X的概率密度为p(x)，则每一赔案的评价赔款额为

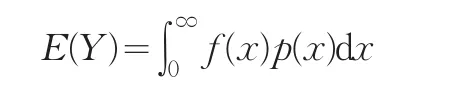
在实际财产保险中，若被保险人将标的足额投保，即保险金额等于标的的实际价值，标的的总价值为S，则赔偿金额的评价赔款额为

另外，被保险人也可以采取绝对免配额、相对免赔额、不足额投保等方式，本文暂不讨论。

同时根据信度理论可以对平均赔款额进行校正，推导略，可得校正后的平均赔款额m

其中，Z=n(n+k)，μ为先验估计，xˉ为通过观察得到的平均值。

通过原始数据易得xˉ=21.3237①，Z=0.9643。μ可以根据前文拟合所得的对数正态分布函数以及公式（6）得到。其中S值的确定成为关键，理论上保险标的上限S应该是无穷大的，根据对数正态分布的一阶矩为

显然实际情况下市场无法承担如此庞大的灾害损失。风暴潮灾害毕竟属于自然灾害的一种形式，不可避免的会出现损失极端大的情况，在我国目前保险市场不发达的情况下，为了避免风险极大状况下保险公司纷纷倒闭的情况，可以对风暴潮灾害损失赔付设定一个上限，当损失超过此上限后，超过部分由国家财政或者民间团体救助等方式进行，以此来保证风暴潮灾害保险的顺利开展。

鉴于对54次风暴潮损失数据的分析，可以采取S=200。通过MATLAB 2008编程计算，μ=3.5329，根据式（7）可得，每次风暴潮损失的平均赔款额为20.6883亿元。为粗略估算沿海个体居民所缴保费，可假设保费筹集区域为风暴潮灾害频发的南方七省（台湾省除外），同时不考虑企业或政府等个体购买保单情况，以七省总人口数α来近似作为被保险人购买保单总数，且保单为同质保单，则沿海七省2009年底总人口为α=3.35亿人。由此可得每人在每次风暴潮发生时仅需付给y=mα=6.17元。即沿海7省每人仅需付6.17元即可享受一次风暴潮灾害带来的损失补偿；另外以平均每年n=5次台风计算，则沿海居民每年所需缴纳的风暴潮保险保费为

即沿海7省每人每年仅付30.88元可应对单次风暴潮总损失最高达200亿元的保险补偿。这对沿海饱受风暴潮影响的居民来说具有重要意义，同时可以大大减少国家财政压力。

3 结论

本文将风暴潮造成的直接经济损失都包括在内，即包括了渔船、沿海养殖、陆上财产等的风险，所发行的风暴潮灾害保险属于财产综合险。经过拟合发现风暴潮灾害并不具有巨灾的性质，可以按照一般非寿险精算方法进行保险定价。这样可避免因单独承保沿海养殖等保险所存在的巨灾的性质，通过综合保险的形式最大程度的包含了众多风暴潮灾害风险，为科学确定沿海居民的风暴潮灾害损失补偿。

在此基础上，本文利用非寿险精算方法对风暴潮灾害保险进行定价，研究发现沿海居民每年所需缴纳的风暴潮保险保费30.88元即可应对总损失最高达200亿元的保险补偿，明显增强了沿海居民对风暴潮灾害保险的应对能力，通过市场化手段提高了对风暴潮灾害的灾后补偿。

[1]卓志,李恒琦,张运刚等.保险精算通论[M].成都：西南财经大学出版社，2006.

[2]王晓军等.保险精算学[M].北京:中国人民大学出版社,1999.

[3]姚众志.论精算方法在火灾等可保风险中的预警作用[J].保险研究,2008，（增刊2）.