QSAR中ANN用于研究变量选择方法的回顾和比较

杨 蕾，王 鹏，王 虹，3，蒋益林

(1.哈尔滨工业大学 基础交叉与科学技术研究院，150001哈尔滨，leiyang84@vip.sina.com;2.哈尔滨工业大学市政环境工程学院，150090哈尔滨;3.黑龙江大学化学化工与材料学院，150080哈尔滨)

在环境化学领域，QSAR是进行有毒化学品生态风险评价的重要手段之一.目前，QSAR研究中常用的方法有多元线性回归分析(MLR)、人工神经网络(ANN)等，后者在处理非线性关系方面有着非常强大的功能，而化合物的结构和毒性之间大多存在非线性的关系，使ANN成为QSAR研究的热点[1－3].

由输入变量ANN便能预测输出变量，但网络内部的作用机理往往被忽略，因而被认为是个黑箱模型.近年来，研究者提出了许多方法来描述变量在神经网络QSAR模型中所起的作用，然而大多数方法被用来消除不相关变量，因而被称为修剪方法[4－6].简单地说，修剪算法就是由具有高度联结的网络(i.e.神经元之间有许多连接)开始，逐步移除弱连接，或当连接移除时，网络误差无明显变化的连接.事实上，在QSAR建模中，不仅需要好的预测能力，还要了解每个输入变量对输出的相对贡献大小.本文回顾和比较了用ANN建模并解释QSAR模型的6种方法，这些方法被用来确定每个输入变量对输出的贡献，因而不是修剪算法.

以35种硝基化合物对黑呆头鱼96 h的生物毒性为研究对象，探讨了ANN中引入变量选择方法后，QSAR模型的解释能力.结果表明，偏微分方法分析所建模型能得出最为全面准确的结果，模型具有良好的预测和解释能力;其次为分布图方法.扰动法和权重法对输入参数能实现较好的分类，但过于简化且方法不稳定;传统的逐步回归法所得结果最差.

1 建模数据库及方法

以文献[7]报道的35种硝基芳烃化合物对黑呆头鱼的96 h半致死浓度cL50(mmol/L)数据作为研究对象，来讨论和比较用于分析和解释人工神经网络QSAR模型的不同方法.该硝基芳烃主要由具有不同硝基取代基的甲苯、苯胺和苯酚、卤代苯组成，具体结构和活性见表1.数据lg1/cL50见文献[7].

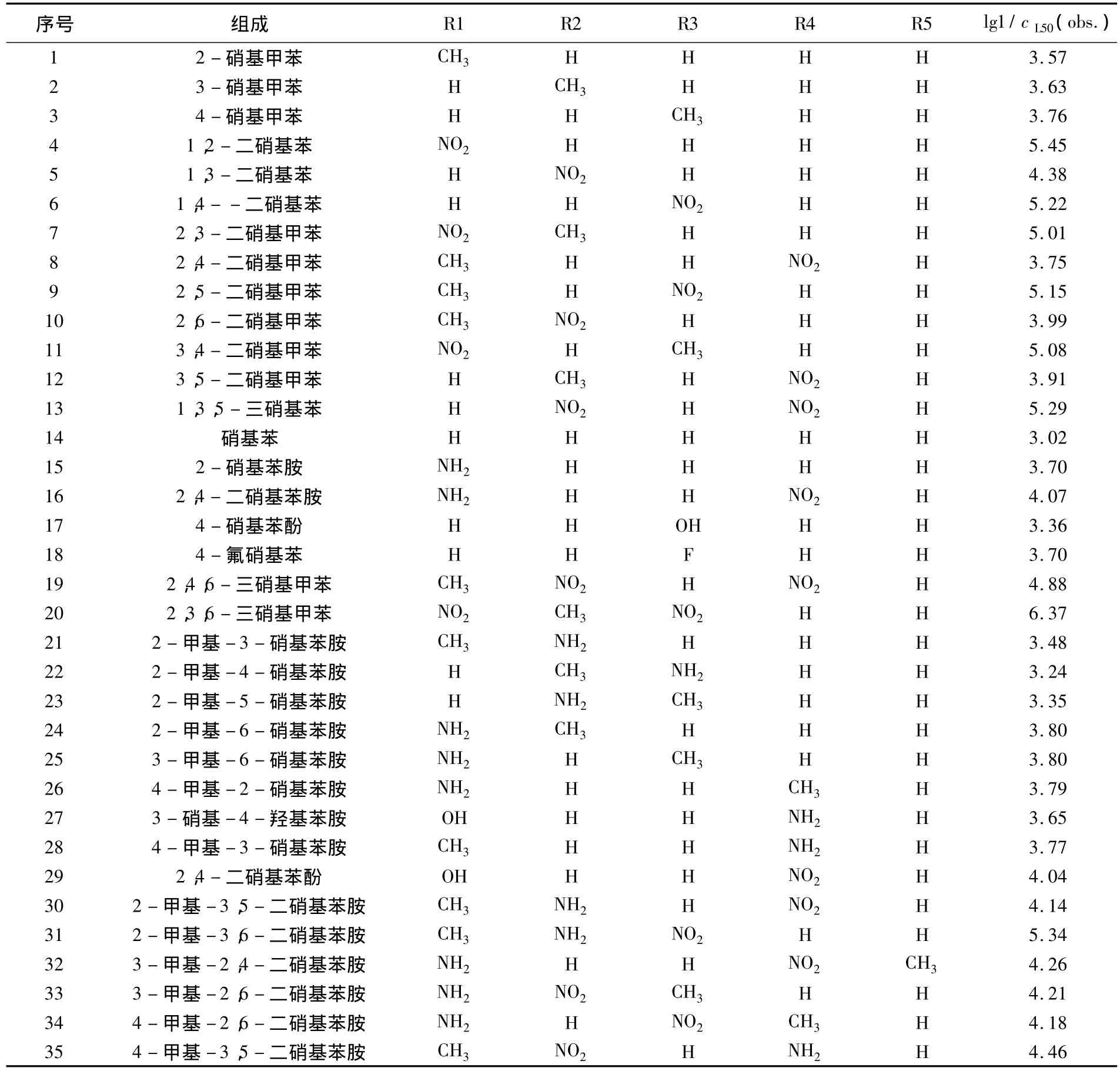
表1 硝基芳烃化合物结构及其毒性

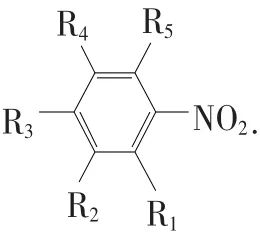
在QSAR研究中，用于描述化合物的结构参数有很多，包括拓扑的、量子的、实验值等[7－9].本文在 Hall[7]和黄庆国等[10]研究硝基芳烃类化合物的基础上，利用HyperChem 6.03软件和自编的C++软件分别计算了7种量子化学参数和5种自相关拓扑指数来表征化合物的结构，具体见表2(为表述方便，以下选择变量方法中都以表中的编号来代替变量).

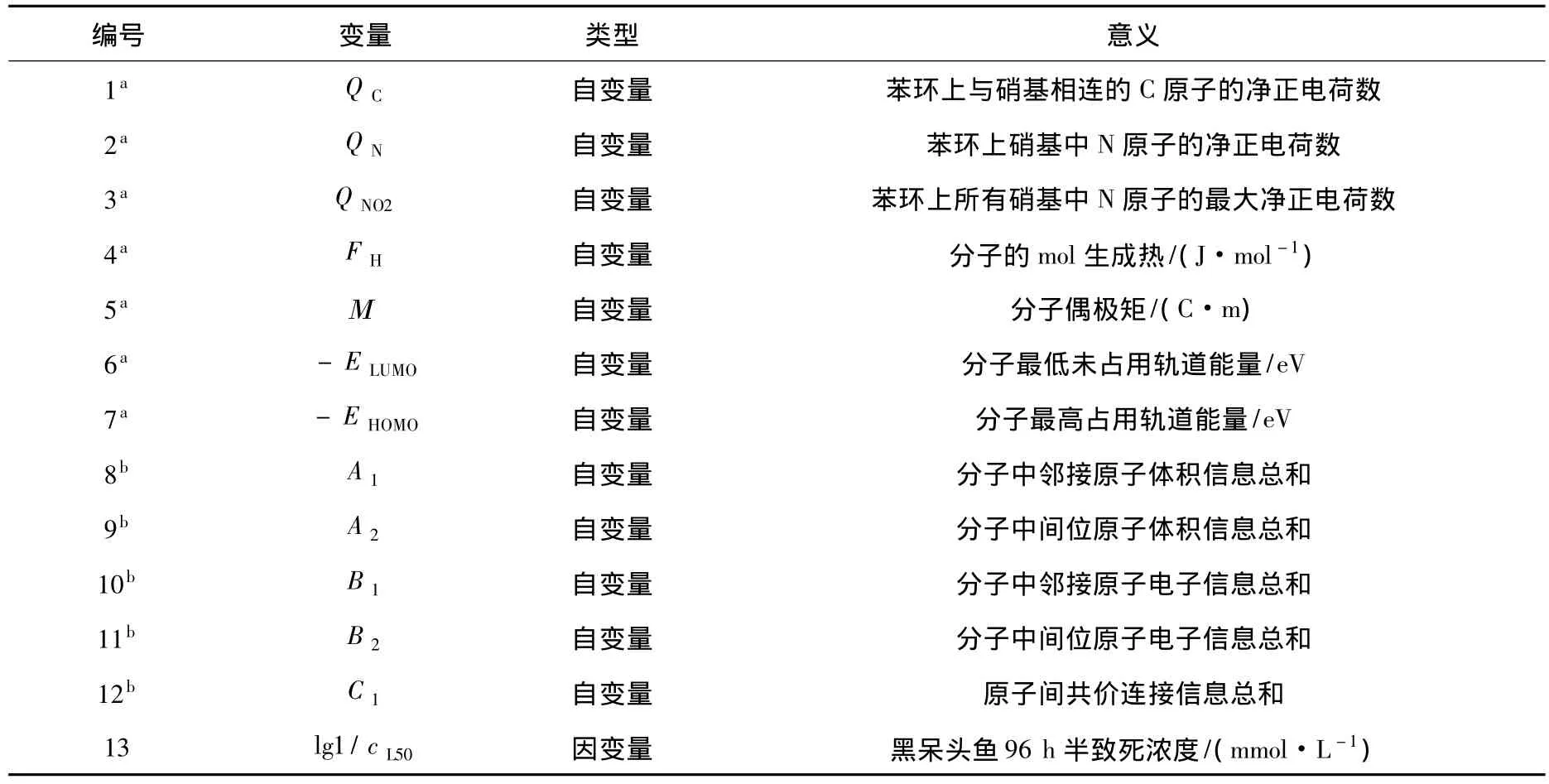
表2 硝基芳烃化合物的量子化学参数和拓扑指数

2 方法

2.1 人工神经网络结构

目前，在QSAR建模中，多层前馈性人工神经网络结构得到了最为广泛的应用，其依据误差反向传播算法训练而得.本文采用较为普遍的3层网络结构(其中输入层12个神经元，隐含层5个神经元和输出层1个神经元)，具体结构见图1.

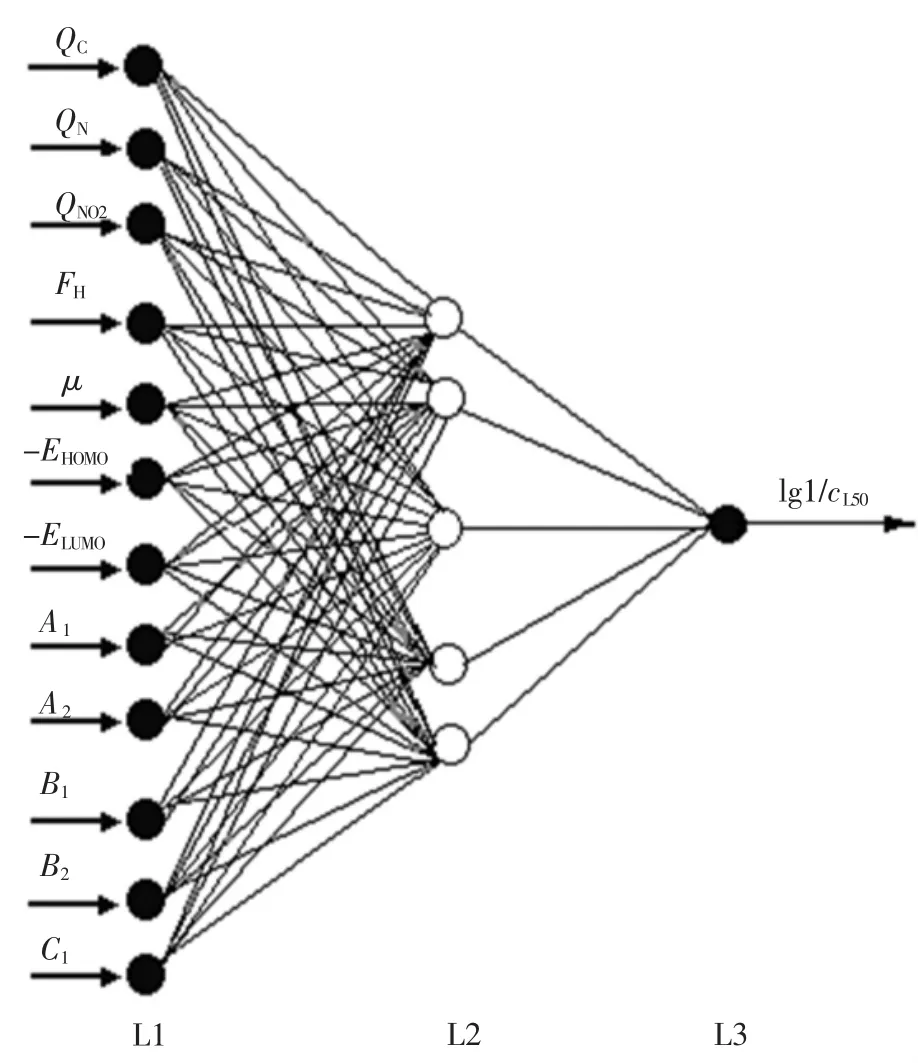
图1 人工神经网络结构

建模过程主要分两步:

1)随机选择75%的化合物作为训练集，25%的化合物作为测试集，利用训练数据集来训练模型，测试集来验证模型，反复多次来确定最佳的网络结构[12];

2)在整个数据集上，利用第一步所获得的网络最佳结构进行QSAR建模，采用不同方法研究输入变量对网络输出，即化合物的生物毒性的相对贡献大小，并分析解释QSAR模型.

2.2 偏微分法

由该法可以获得两种结果:一是每个输入变量的微小变化导致网络输出变化的偏微分图;二是每个输入变量相对输出的贡献大小排序.

为了获得输入变量的微小变化导致输出变化的偏微分图，计算输出对输入变量的偏微分.以具有ni个输入节点、nh个隐含节点和1个输出节点，第j个样本的输出yj关于输入xj(j=1…N，N为样本总数)的偏微分为

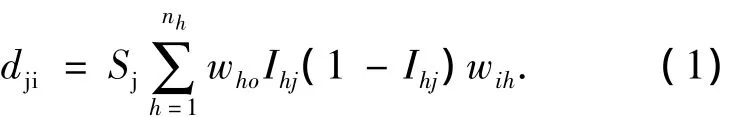
其中:Sj为输出神经元对其输入的偏微分;Ihj为第h个神经元的响应;who和wih分别为输出与第h个隐含层神经元、第i个输入神经元与第h个隐含神经元之间的连接权重.

由式(1)可获得一系列输出相对输入变量的偏微分图，能直接评价每个输入对输出的影响.例如，偏微分为负，对于研究变量，输出随输入的增大而减小.

另外，对于整个数据集，由偏微分方法可得到ANN输出对每个输入变量的相对贡献大小，具体计算如下:

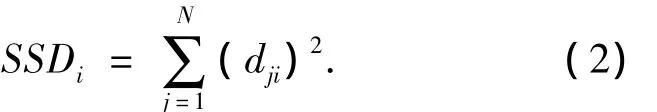
其中:SSDi为第i个变量对所有化合物毒性网络输出的偏微分平方之和，SSD值越大，其对网络输出，即对化合物毒性的影响最大.

2.3 扰动法

该法旨在评价每个输入的微小变化对ANN输出的影响.算法首先调整一个变量的值，而保持其他变量不变，同时记下每个输入对输出的响应.输入变量变化对输出影响最大的变量被视为对网络输出影响最大[13]，为最重要的变量.

基本思想如下:假定xi为选定变量，δ为变化量，则xi的变化可表示为xi=xi+δ.一般δ可选定变量值的10%～50%不等，这样便可获得按重要性排序的输入变量分类.

2.4 权重方法

该法通过分割网络连接权重来确定输入变量的相对重要性，是由 Garson[14]首先提出的.方法主要涉及两部分:一是按隐含层节点分割隐含－输出层间连接权重;二是按输入层节点划分输入－隐含层间连接权重.本文对此方法进行了简化，而所得结果一致，具体如下:

1)对于隐含神经元h，用其输入－隐含层连接权重的绝对值除以所有输入－隐含层间的连接权重绝对值之和，即

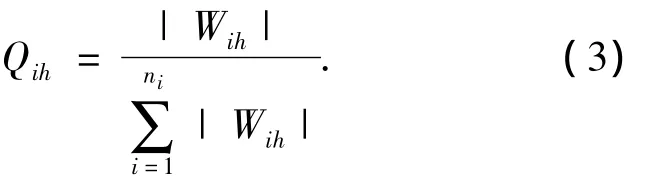
2)对于输入神经元i，用每个隐含神经元与其连接的输入所获得的Qih之和，除以所有隐含神经元与其连接的输入所获得的Qih之和，再乘以100便可获得每个输入变量对所有样本输出，权重分布贡献的相对重要性(Relative Importance)，即

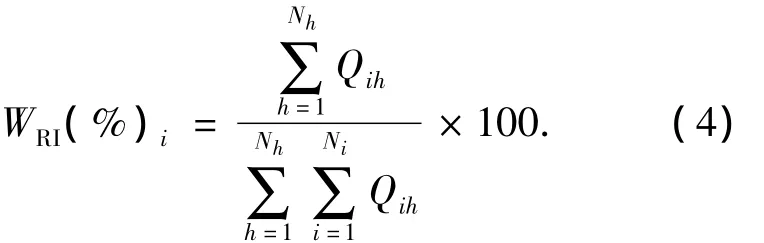
2.5 轮廓图法

Lek等[15]首先提出了该方法，其主要思想是构建隶属于所有输入变量范围的假定矩阵，同一时刻固定其他变量的值，在假定矩阵范围内连续变化某个输入变量来观察网络输出的变化.详细地说，就是每个输入变量在区间范围内被分成等间距的一系列值，该间距被称为标度.其他变量被依次固定在不同倍数的标度上，一般取5个点，分别是最小值、1/4区间、1/2区间、3/4区间和最大值上.对于每个输入变量，根据不同的取值，便可得到输出变量的分布图.由分布曲线图(见图3)可以直观地看到随着输入变量的递增，网络输出变量的变化趋势和垂直波动范围，波动范围越大，表明该变量越重要.

本文在利用轮廓图法研究输入变量对输出贡献的过程中，分别将输入变量的最大值和最小值区间范围分成12、24、48、96、144 和 192 标度.图 3代表了24标度的轮廓图.事实上，不管采用什么标度，该方法相当稳定，不同标度下变量的轮廓图具有相似的形状，唯一不同的是标度越大，变量的轮廓图越精细.

2.6 传统逐步回归法

该法主要包括逐步地增加或删除一个输入变量来考察对输出结果的影响，根据网络输出均方差(MSE)的变化，输入变量便能按照重要性进行排序.例如在逐步减少输入变量个数的过程中，引起均方差最大程度增大的变量，便是问题空间最重要的变量[16];反之，在逐步增加输入变量的过程中，引起均方差最大程度减小的变量，便是问题空间最重要的变量.本文利用这两种逐步回归建模方法来评价12个输入变量的影响，分别可以获得变量之间的相对重要性排序.

1)前进法:首先产生12个模型，每个模型仅包含一个输入变量，产生最小误差的变量x最为重要，并参与下一步建模;接着产生11个模型，每个模型由x和剩余变量中的任意一个组成，这个过程反复进行，直到所有的变量都进入模型.网络模型中输入变量的出现排序即为它们对网络输出的相对重要性关系;

2)后退法:首先产生12个模型，每个模型由11个变量组成，如果模型中不包含变量x引起网络输出的最大误差，则该变量x最为重要;接着产生11个模型，每个ANN模型由10个输入变量组成.这个过程反复进行，直到模型中剩下一个变量为止.网络中输入变量的消除顺序即为它们对网络输出的重要性排序.

3 结果与讨论

3.1 ANN－QSAR模型的预测能力

由2.1给出的建模过程，最终确定最佳网络结构为12－5－1(见图1).对于化合物学习样本集，步骤 1(见 2.1)的结果为 R2=0.923(P＜0.01);对于测试样本集，其结果为 R2=0.930(P＜0.01).这表明该网络结构可以应用于步骤2(见2.1)，即分析结构参数对所有化合物毒性的相对重要性.所有样本参与建模，结果为R2=0.938(P＜0.01)，验证了该网络模型的预测能力.

3.2 不同方法选择变量结果及其比较

3.2.1 偏微分方法

由偏微分方法可以获得一系列输入变量对输出的偏微分图.图2给出了QNO2对硝基芳烃化合物毒性lg1/cL50的偏微分图.可以看出，其偏微分值都为正，且随着QNO2的增大，偏微分接近于0，表明随着QNO2的增大，lg1/cL50也随之增大并最终达到一个稳定值，类似情况的还有变量QC、QN、FH、－ ELUMO、A2，其中 QN无明显的规律性;此外变量 μ、－ EHOMO、A1、B1、B2、C1对硝基芳烃化合物毒性lg1/CL50的偏微分值大多为负，其中μ、B1无明显的规律性.

图2 ANN网络输出lg1/cL50对变量QNO2的偏微分图

3.2.2 轮廓图法

图3代表了24标度的轮廓图，可以看出，网络输出lg1/cL50随QNO2、B2和 － EHOMO的增大有明显变化，其中QNO2在整个取值范围内对网络输出影响最大，是最重要的变量.另外，lg1/cL50随QNO2的增大而增大，且当QNO2增大到一定程度时，lg1/cL50保持恒定，而B2和－EHOMO的增大将导致lg1/cL50减小，这与偏微分方法所得结果一致.由轮廓图法获得的变量间的相对重要性关系见表3.

3.2.3 权重法和扰动法

图4(a)给出了由偏微分图得到的输入变量对输出的相对贡献图，可以看出，该方法非常的稳定且有较小的置信度区间，QNO2是化合物结构变量中对生物毒性贡献最大的变量(45.2%)，其次是－ELUMO(16.1%)和B2(11.3%).由权重方法获得输入变量对输出的相对贡献率见图4(b).与偏微分方法比较，其置信度区间更大，因而稳定性较差.由图可见，QNO2变量对网络输出的贡献率最大，其次为 － ELUMO、QC、FH和 B2，而其他变量贡献率差异不大.

图3 12个参数变量对网络输出lg1/cL50的轮廓图

图4(c)给出了利用扰动法(δ=50%)获得的输入对输出的相对贡献分布图.由图可见，QNO2变量对网络输出的贡献率最大，其次为 QC、－ELUMO和B2.该方法同样也不够稳定，因为有些变量如QN和A2、－EHOMO和B1等之间对输出的贡献差异并不明显.

3.2.4 逐步回归法

逐步回归方法分为前进法和后退法，获得的变量之间的相对重要性排序结果见表3，可以看出，除了最重要的变量QNO2，两种方法对变量重要性分类结果不尽相同.根据前进法，QNO2之后依次为FH、QC、－ EHOMO，而后退法依次为QC、－ ELUMO、QN.

3.3 ANN－QSAR模型的解释性能力

本文采用12－5－1的3层神经网络结构，对硝基芳烃对黑呆头鱼生物毒性进行QSAR建模，并将各种选择变量方法作用于模型，来研究不同变量对网络输出，即生物毒性的相对重要性，进而来阐释硝基芳烃化合物的作用机理，提高网络模型的解释能力.

早期的研究表明[17]，硝基芳烃化合物是一类重要的遗传毒性化合物，其致毒机理为:苯环上硝基N原子的亲电中心与生物组织中作为亲核中心的DNA分子相互反应引起的.

结构参数QNO2是用来表征苯环上所有硝基中N原子的最大净正电荷数，由表3可以看出，所有变量选择方法都得出QNO2是影响化合物毒性的最重要参数，这正好验证了文献[17]所报道的该类化合物的致毒机理.

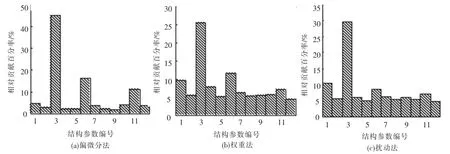
图4 不同方法获得的12个结构参数对ANN输出的相对贡献分布图

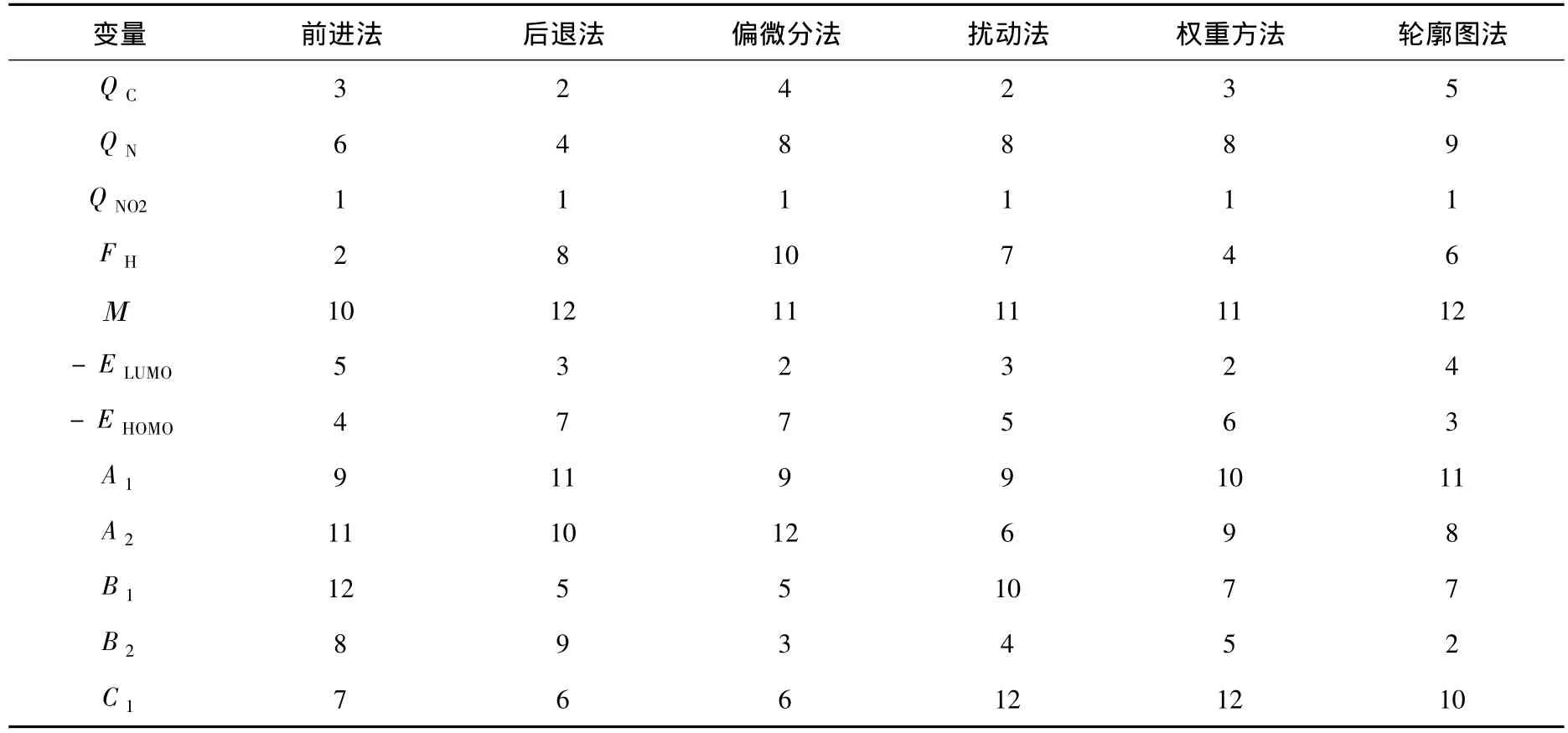
表3 采用不同方法对输入变量相对重要性分类结果

比较表3和图4可以看出，－ELUMO、QC、B2是另外3个影响硝基芳烃毒性的重要结构参数.

其中－ELUMO表示分子最低未占用轨道能量，其值愈大，接受电子的能力越强，化合物对黑呆头鱼毒性也越大.这表明－ELUMO与生物毒性之间正相关，这与偏微分法和轮廓图法所得的结论一致.可以认为，当化合物的亲电中心与DNA分子的亲核中心发生反应时，－ELUMO越大则化合物越容易接受电子发生反应，因而化合物的生物毒性越强.

QC代表苯环上与硝基相连的C原子的净正电荷数，其值越大，则与之相邻的硝基N原子亲电中心越强，越容易与DNA分子反应，因而QC与化合物毒性之间正相关，这与偏微分法的结论一致.

自相关拓扑指数B2代表分子中间位原子电子信息总和，可以认为取代基电子相互作用同样影响了DNA分子的反应活性.供电基团，如NH2、CH3、OH(见表1)可能离域了硝基上N原子的正电荷，提高了反应的活化能，因而化合物的毒性与B2负相关，这与偏微分和轮廓图方法所得结论一致.

利用不同的变量选择方法，剩余变量的相对贡献大小排序有较大的出入，这主要是由方法的局限性引起的.不管怎样，ANN中引入选择方法有助于识别影响问题空间的主因子，提高模型的解释能力.

4 结论

1)在ANN中引入不同的变量选择方法，可大大增强QSAR模型的解释能力，其中偏微分方法能得出最为全面准确的结果，其次为轮廓图方法.扰动法和权重法对输入参数能实现较好的分类，但过于简化且方法不稳定;而传统的逐步回归法结果最差.

2)硝基芳烃对黑呆头鱼毒性的QSAR模型中，选择方法识别的重要变量包括QNO2、－ELUMO、QC和B2，它们能准确揭示化合物的致毒机理，从而证明了变量选择方法的有效性.

[1]WU J H，MEI J，WEN S X，et al.A self－adaptive genetic algorithm－artificial neural network algorithm with leave－one－out cross validation for descriptor selection in QSAR study[J].Journal of Computational Chemistry，2010，31(10):1956 －1968.

[2]JAGDISH C P，ONKAR S.Artificial neural networksbased approach to design ARIs using QSAR for diabetes mellitus[J].Journal of Computational Chemistry，2009，30(15):2494－2508.

[3]JAGDISH C P，BOON H C.Artificial neural networkbased drug design for diabetes mellitus using flavonoids[J].Journal of Computational Chemistry，2011，32(4):555－567.

[4]APILAK W，CHANIN N，THANAKORN N，et al.Modeling the activity of furin inhibitors using artificial neural network[J].European Journal of Medicinal Chemistry，2008，44:1664 －1673.

[5]陈国华，陆瑶，陈虹.基于逐步回归所得变量集的遗传反向传播神经网络的QSAR研究[J].计算机与应用化学，2010，27(9):1257 －1262.

[6]杜雨静，范英芳.人工神经网络用于三苯基丙烯腈衍生物的定量结构 －活性关系模型[J].化工进展，2010，29(1):25 －28.

[7]KIER L B，HALL L H.Molecular connectivity in structure － activity analysis[M].[S.l.]:Research Studies Press，1987:232 －256.

[8]李鸣建，冯长君.取代苯甲酸对植物生长调节活性的拓扑QSAR研究[J].哈尔滨工业大学学报，2009，41(5):195－197.

[9]陈炫，聂长明，蒋司同，等.量子拓扑方法对硫醇的定量构效关系研究[J].南华大学学报，2009，23(4):84－87.

[10]HUANG Qingguo，LIU Yongbin.Genotoxicity of substituted nitro benzenes and the quantitative structureactivity relationship[J].Journal of Environmental Sciences，1996，8:103 －109.

[11]于秀娟，王鹏，龙明策，等.有机化学品点价自相关拓扑指数与生物降解性的定量关系[J].环境科学学报，2000，20(增刊):93 －96.

[12]GEMAN S，BIENENSTOCK E，DOURSAT R.Neural networks and the bias/valance dilemma[J].Neural Computation，1992，4(3):51 －58.

[13]SCARDI M，HARDING L W.Developing an empirical model of phytoplankton primary production:a neural network case study[J].Ecological Modelling，1999，120(2/3):213－223.

[14]GARSON G D.Interpreting neural－network connection weight[J].Artificial Intelligence，2001，6(8):47 －51.

[15]LEK S，DELACOSTE M，BARAN P，et al.Application of neural networks to modelling nonlinear relationships in ecology[J].Ecological Modelling，1996，90(32):39－52.

[16]SUNG A H.Ranking importance of input parameters of neural networks[J].Expert Systems with Applications，1998，15(12):405 －411.

[17]沈洪艳，张国霞，刘宝友，等.地表水体中常见硝基芳烃对鲤鱼的联合毒性[J].环境科学与技术，2011，34(2):17 －21.