预制混凝土插入式预留孔灌浆钢筋搭接试验

姜洪斌，张海顺，2，刘文清，闫红缨

(1.哈尔滨工业大学 土木工程学院，150090哈尔滨，3260787@hit.edu.cn;2.天津大学 建筑工程学院，300072天津;3.黑龙江宇辉建设集团，150090哈尔滨)

“插入式预留孔灌浆钢筋搭接连接”是课题组研发的具有自主知识产权的预制装配整体式混凝土结构钢筋连接方法[1]，该方法具有连接简便、质量易保障、成本低廉等优势[2－4].插入式预留孔灌浆钢筋搭接连接基本原理是:搭接钢筋之间能够传力是由于钢筋与混凝土之间的粘结锚固[5－7].两根相向受力的钢筋分别锚固在搭接连接区段的混凝土中而将力传递给混凝土，从而实现钢筋之间应力的传递[8－9].钢筋的搭接长度是插入式预留孔灌浆钢筋连接的受力性能关键[10－12].

1 试验概况

1.1 插入式预留孔灌浆钢筋连接具体实施方式

如图1所示，在预制混凝土构件预埋钢筋旁边的孔洞内，插入被连接钢筋至设定搭接长度，通过向孔洞内灌入灌浆料并经其凝结硬化后即可将2根钢筋连接成为一体.在钢筋搭接长度范围内沿周边布置约束螺旋筋，用以加强钢筋的搭接连接性能.

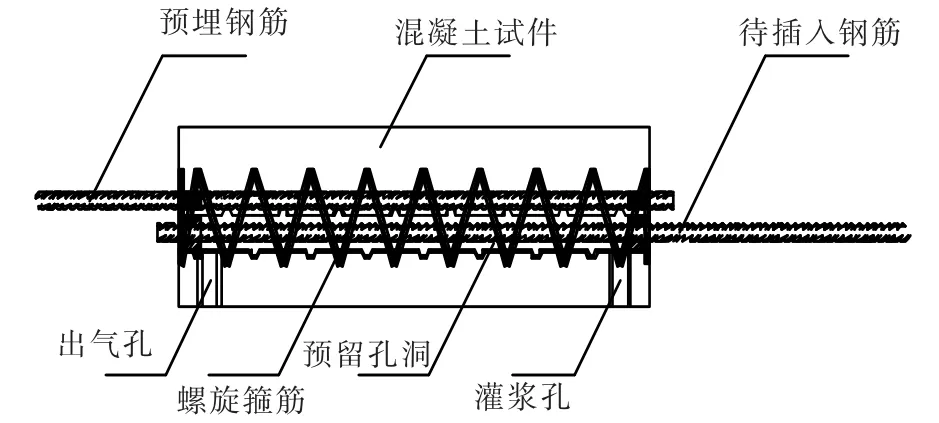
图1 钢筋搭接示意

1.2 钢筋搭接试验试件设计

本次试验为住宅产业化下装配式施工模式的钢筋搭接，钢筋搭接接头面积百分率均为100%，钢筋搭接长度ll=1.6 la，la为规范要求的基本锚固长度.考虑螺旋筋套箍作用的有利影响，搭接长度分别减少20%、30%、40%，即搭接长度确定为0.8 ll、0.7 ll、0.6 ll.混凝土采用 C20、C30、C40，钢筋为 HRB335，直径分别为 12、14、16 mm.同时制备一些 0.5 ll、0.4 ll、0.3 ll的试件，以便确定搭接长度极限和可靠度分析.

钢筋搭接试验试件尺寸见图2和表1.试件截面为150 mm×150 mm，长度为钢筋搭接左右各增加20 mm的非粘结段.预埋钢筋的尺寸为混凝土内部的钢筋左右分别伸出20和190 mm，后插钢筋的尺寸为混凝土内部的钢筋左右分别伸出20和460 mm.内部螺旋箍筋采用4钢筋，环内径80 mm.

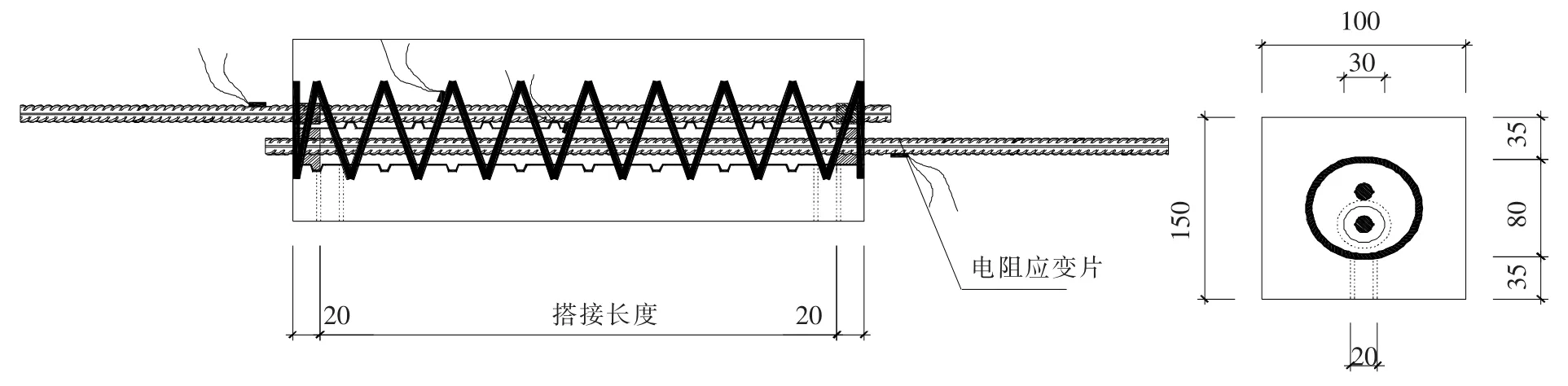
图2 钢筋搭接试验试件尺寸(mm)

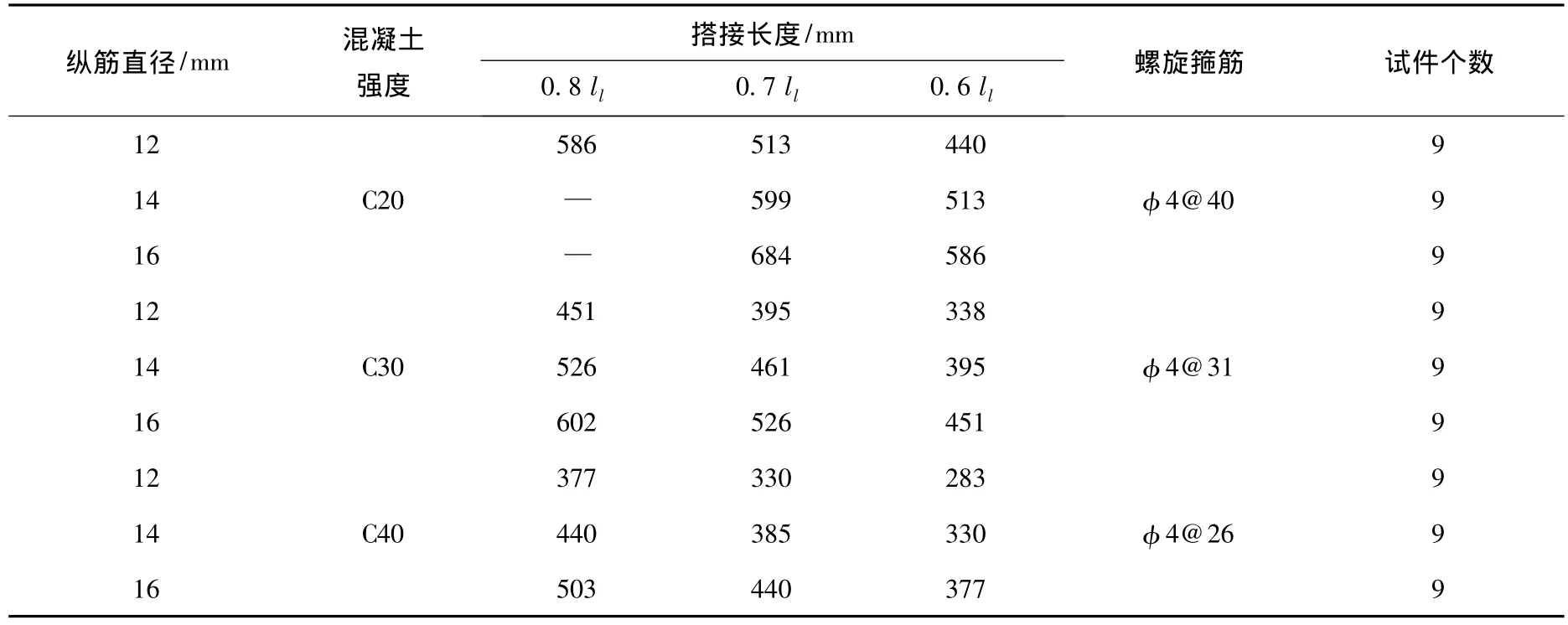
表1 钢筋搭接试验试件尺寸

1.3 钢筋搭接试验试件制备

1)将螺纹钢管，预埋钢筋和螺旋筋放入特制钢模中，预埋钢筋的一端伸出钢模20 mm，螺旋筋的1/4处应变片的位置靠近预埋筋伸出钢模较短的一侧，见图3.

图3 螺纹钢管、预埋钢筋和螺旋筋放入钢模中

2)浇筑混凝土，在混凝土初凝后抽出螺纹钢管，形成预留孔，见图4.

3)插入后插钢筋，灌入灌浆料，养护28 d，见图5.

1.4 钢筋搭接试验方案

采用单向拉伸的方法进行钢筋搭接性能试验，用于加载的钢架为长度可调，加载设备采用200 kN穿心式液压千斤顶，见图6.就位后试件的加载端钢筋分别伸出加载钢架，其中一端采用夹片式锚具锚固于加载钢架底板，另一端穿过千斤顶并用夹片式锚具锚固.试件的自由端钢筋架设千分表测量滑移量.

图4 混凝土试件和孔洞

图5 钢筋混凝土搭接试件完成

图6 试验装置

拉伸试验加载为连续方式，直到钢筋屈服或破坏为止.露出试件外部的纵筋、及内部螺旋筋在试件长度1/4和1/2处贴有应变片，试验中记录了拉伸力、钢筋应变和钢筋自由端滑移.

2 钢筋搭接试验数据和处理

2.1 试验现象及结果

每组试件共3个，其中1个加载至钢筋拉断，2个加载至钢筋屈服.试验时试件混凝土破坏现象有所不同，见图7，当混凝土试件长度较长(0.8 ll)时，加载端和自由端的混凝土开裂较小;而长度中等(0.7 ll)时，开裂较大;当长度更短(0.6 ll)时，加载端和自由端混凝土压碎破坏.

将各个试件的试验结果汇总，见表2.在各个试验中，所有受拉钢筋均达到屈服或拉断，但钢筋均未被抽出，未发现钢筋混凝土粘结段出现粘结滑移.试验结果充分证明，试验设计的搭接形式和搭接长度满足搭接要求.

图7 搭接试件破坏图

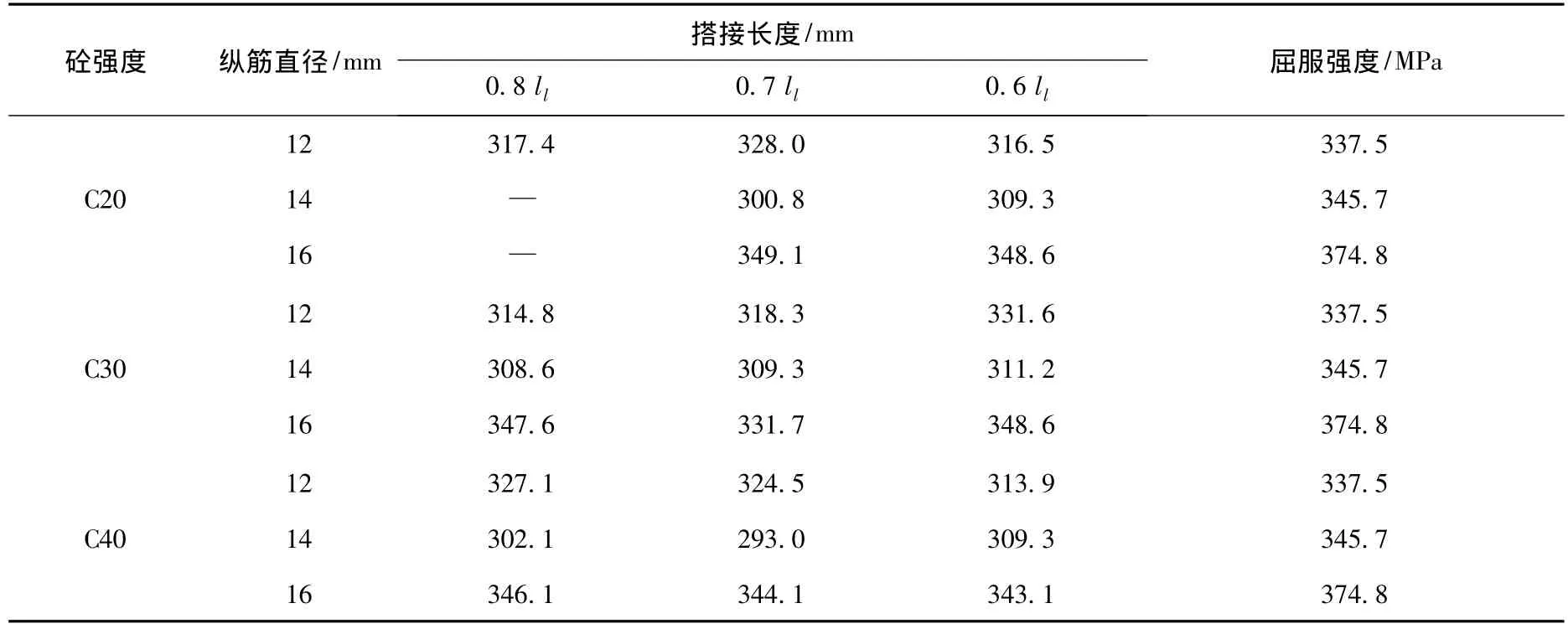
表2 钢筋搭接长度屈服强度值

2.2 螺旋筋应力应变分析

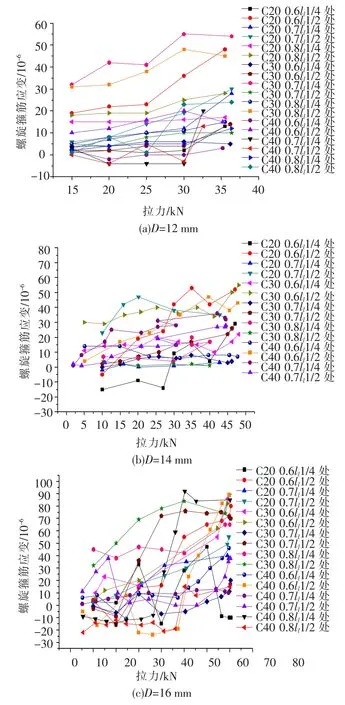
图8 各个试件螺旋筋拉力－应变折线

图8为不同钢筋直径各试件内部螺旋筋应变.试件1/2处应变增长较快，边界1/4处应变增长较慢，原因为端部套箍作用强，约束较多，所以端部应变增长较慢.但是总体应变值均很小，都在1 ×10－4以内.

在钢筋搭接拉拔试验中，螺旋筋主要作用是侧向约束混凝土开裂，而拉拔力在钢筋混凝土交界面形成的剪切力很大部分由混凝土内部粘结力消耗传递，所以螺旋筋受力较小，其应变值也就很小.同时发现从12、14、16 mm的钢筋直径逐渐增加，其螺旋筋的应变值也逐渐变得不稳定，原因为随着钢筋直径的增加，屈服拉力也变大，同时钢筋表面积的也逐渐增加，粘结应力分布也越来越不规则，导致混凝土对钢筋的握裹力不稳定，最终导致螺旋箍筋的应变变化不规则.

3 钢筋极限搭接长度分析

3.1 极限搭接长度试验

为了深入研究极限钢筋搭接长度，试验进行了钢筋搭接长度继续减小到0.5 ll、0.4 ll、0.3 ll的拉拔试验.如表3所示，混凝土采用C30，钢筋HRB335，直径分别为 12、14、16 mm.混凝土试件截面尺寸为150 mm×150 mm，试件分别每组为3个、共9组，计27个试件.

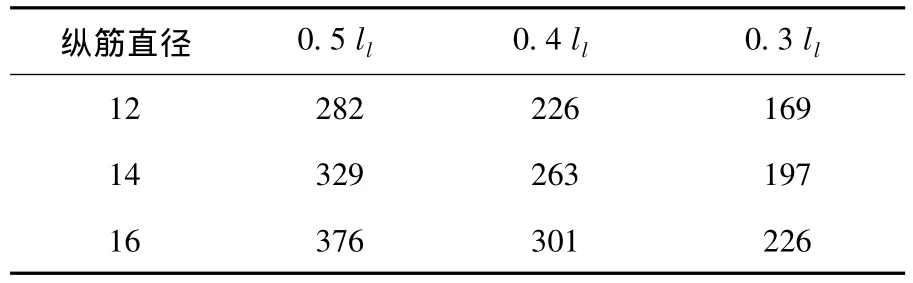
表3 极限搭接长度试验参数 mm

3.2 极限搭接长度试验数据处理及结果

表4列出了钢筋搭接长度的试验数据，各个拉力值均为屈服拉应力，在试验中，0.5 ll的所有试件在钢筋屈服时未发现千分表有读数，即认为钢筋混凝土之间未发生粘结滑移.而0.4 ll和0.3ll的试件在钢筋未达到屈服时就已经有很大的滑移量，即认为0.4 ll和0.3 ll搭接长度失败且不可取.可初步认定极限搭接长度为0.5 ll.

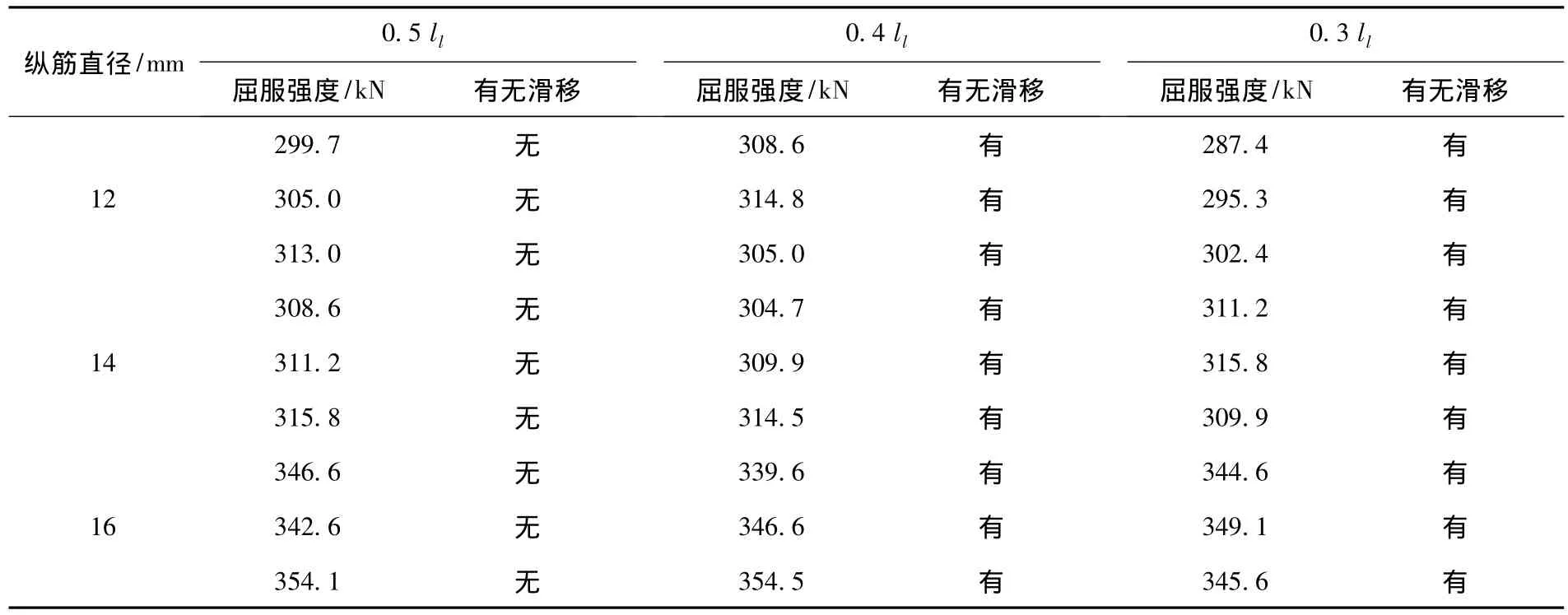
表4 钢筋搭接长度屈服强度及滑移

建议搭接长度ll=1.25×0.5×1.6la=la，其中1.25为可靠度安全系数;la为规范要求的基本锚固长度.由于螺旋筋的套箍作用，搭接长度可以减短为基本锚固长度，即插入式预留孔灌浆钢筋搭接长度计算公式为

3.3 极限搭接长度机理分析

如图9所示，将螺旋箍筋约束的搭接纵筋作为力学分析模型，在纵筋受拉时产生沿钢筋表面的切向粘结应力τ，由于钢筋表面变形凸起而产生法向应力σ，该法向应力σ是引起搭接范围内混凝土受拉开裂并导致纵筋搭接破坏的原因，因此以混凝土达到抗拉强度为标志，建立力的平衡方程为

式中:σs为混凝土即将开裂时约束螺旋箍筋应力值，σs=αEftk;Asv为约束螺旋加强箍筋截面面积，mm2;ftk为混凝土抗拉强度标准值，N/mm2;Dcor为螺旋筋约束核心混凝土直径，mm;d为纵筋直径，mm;Sv为约束螺旋加强箍筋间距，mm;σ为纵筋表面法向应力，N/mm2.

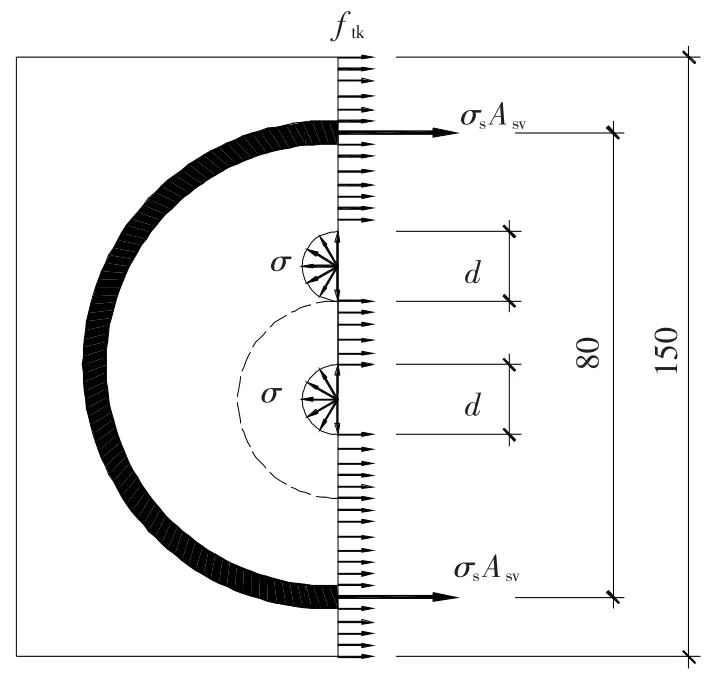
图9 螺旋筋约束力学模型

如图10所示，宏观上在钢筋搭接长度ll范围内，当纵筋受拉达到抗拉强度标准值fyk时，可建立力平衡方程为

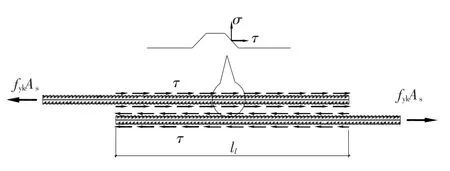
图10 螺旋筋约束力学模型

另外假设，纵筋表面的切向粘结应力τ等于法向应力σ，则有

由式(3)和式(4)联立得法向应力为

式(5)代入式(2)有

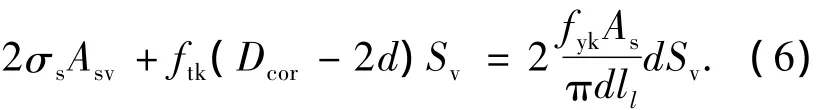
经整理，得纵筋搭接长度为

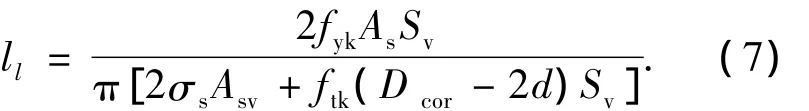
式(7)的意义为，建立起了纵筋搭接连接时，搭接长度ll与约束螺旋箍筋配筋量之间的关系.

由式(7)计算的本试验试件的理论搭接长度见表5.表中计算值较为接近式(1)的试验结论值，且有一定的安全贮备，式(7)可作为螺旋箍筋约束情况下的纵筋搭接长度设计计算公式.

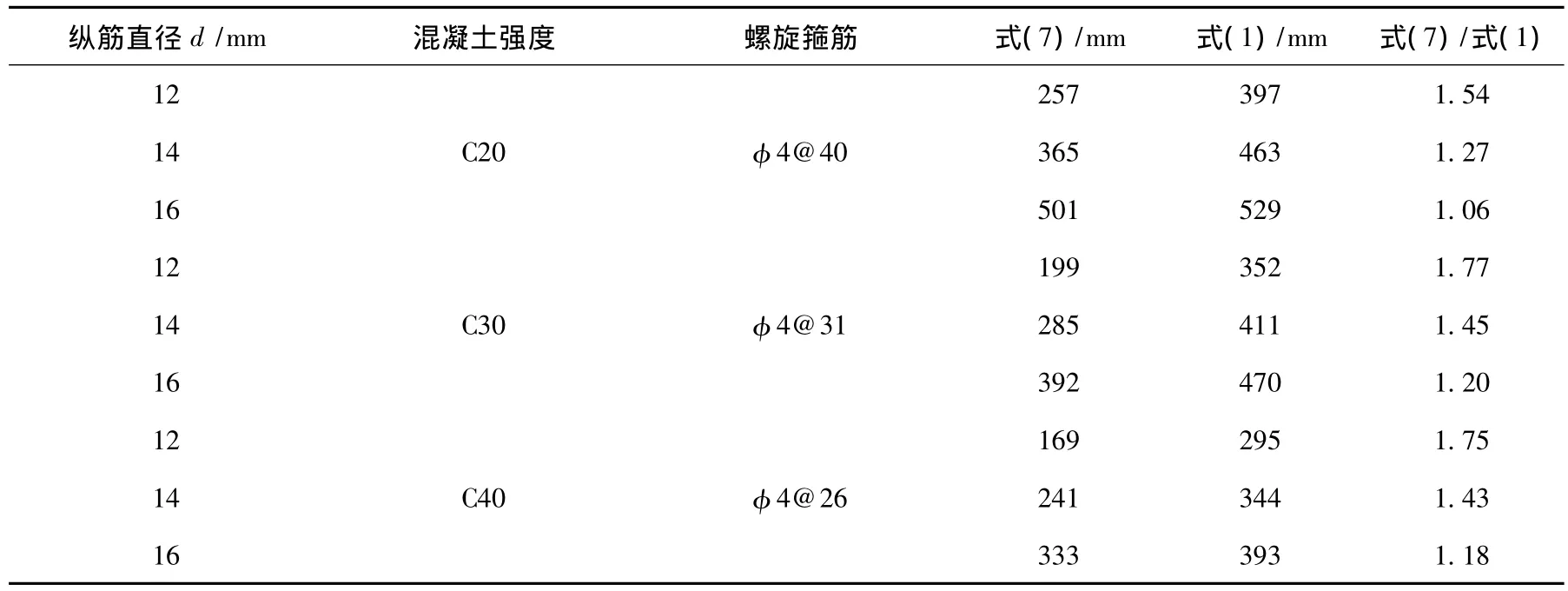
表5 理论搭接长度计算

4 结语

根据不同钢筋直径、混凝土强度、不同搭接长度等因素完成了108个试件的搭接试验，对规范要求搭接长度进行折减20% ～70%设计并试验，得到了插入式预留孔灌浆钢筋搭接连接的破坏模式及各因素的影响规律，分析了螺旋箍筋约束情况下纵筋搭接连接机理，给出了考虑螺旋箍筋配筋量的纵筋搭接长度设计计算方法.经理论分析和试验验证，在配置螺旋箍筋情况下，纵筋的搭接长度可以减短为基本锚固长度，即ll=la.

本文仅在单根钢筋搭接并配置螺旋筋的情况下，进行了单向拉伸试验的探索性初步研究，下一步试验研究拟补充不设螺旋筋套箍的对比试验、及多种受力工况试验，并将这种钢筋连接方式应用到构件试验中，以检验多根钢筋搭接下的受力情况.

[1]张海顺.预制混凝土结构插入式预留孔灌浆钢筋锚固搭接试验研究[D].哈尔滨:哈尔滨工业大学，2009.

[2]PCa技術研究会.プレキャストコンクリート技術マニュァル[M].东京:株式会社彰国社，2000:38－47.

[3]渡辺邦夫，中野清司.知ちれざるPC建築[M].东京:株式会社建筑技术，2004:152－171.

[4]鯉田和夫.最新建築施工[M].东京:技报堂出版株式会社，2008:82－83.

[5]徐有邻.钢筋混凝土粘结锚固性能试验研究[D].北京:清华大学，1990.

[6]王艺霖.钢筋与混凝土粘结性能的若干间题研究[D].武汉:华中科技大学，2005.

[7]PARK R，PAULY T.Reinforced concrete structures[M].New York:John Wiley and Sons Ins，1982:236 －296.

[8]王国杰.高强度自密实混凝土及其与钢筋粘结锚固性能的试验研究[D].福州:福州大学，2002.

[9]MAGNUSSON J.Bond and anchorage of ribbed bars in high-strength concrete[D].Goteborg，Sweden:Division of Concrete Structures，Dept of Structural Engineering，Chalmers University of Technology，2000.

[10]宋玉普，赵国藩.钢筋与混凝土之间的粘结滑移性能研究[J].大连工学院学报，1987，26(2):93－100.

[11]NAMMUR G，Jr，NAAMAN A E.Bond stress model for fiber reinforced concrete based on bond stress-slip relationship[J].ACI Materials，1989，86(1):45 －57.

[12]LUTZ L A.Analysis of stresses in concrete near a reinforcing bar due to bond and transverse cracking[J].ACI Journal，1970，67(10):778 －787.