双曲正切函数在事故黑点鉴别中的应用

杨 轸，唐 莹，方守恩

(同济大学交通运输工程学院，201804上海，yangzhen2276@263.net)

交通事故在道路上是非均匀分布的，道路路段中具有突出事故频率的事故位置被称为事故黑点.传统的事故黑点鉴别方法有事故数法、事故率法、传统贝叶斯法等，近年来，国内外交通安全领域学者对事故黑点鉴别作了很多深入的研究，提出了经验贝叶斯法、质量控制法、累计频率法等[1－7].

其中累计频率法被广泛地应用于公路事故黑点的鉴别中，它特别适应中国目前基础数据相对缺乏，各地道路安全状况差别大的实际情况[8].

在累计频率法中，需要选取合适的公式对累计频率散点图进行拟合，拟合公式的选取对黑点鉴别有一定的影响.常用的拟合公式有多项式、指数函数和双指数函数等，其中中华人民共和国公共安全行业标准《道路交通事故多发位置认定方法(征求意见稿)》提出采用双指数函数作为累计频率法的拟合公式.在实际使用中，这些拟合公式或多或少都存在一定的缺陷，多项式拟合单调性很差，指数函数和双指数函数y=a×ebx+c×edx单调性较好，通常效果也不错，但当路段事故集中程度很高或者事故统计时间很长时，曲线拟合的相关性变差，需要提出一种适应性更好的拟合函数.

此外，以往的事故黑点鉴别方法中，尚未有学者对鉴别结果的有效性进行研究，特别是定量分析不同累计交通量和不同检测方法对事故黑点鉴定的检出率和误检率的影响.《道路交通事故多发位置认定方法(征求意见稿)》中要求分析所用的事故数据时间为1～3 a，但并未就统计年限对检出率和误检率的影响进行详细说明，并且不同的道路其交通量和事故率差异很大，用单一的统计时间来限定值得商榷.

由于事故发生具有随机性，仅从事故的统计结果不能直接推导出路段事故率的期望值.为此，本文提出了基于随机仿真的黑点位置鉴别比较方法，其思路为:首先从多年运营的代表性道路的事故资料中分别统计获得各路段单元的事故率;然后，根据该事故率组按照事故发生统计规律通过计算机模拟产生不同累计交通量下一系列事故数据，并根据这些数据采用不同的拟合方法进行黑点鉴别;最后，将拟合结果同期望事故黑点域进行比较，分析不同鉴别方法在曲线拟合相关性，不同累计交通量下事故黑点检出率、误检率等方面的差异以推荐最佳的鉴别方法及适应条件.考虑到仿真的随机性，可以采用多次仿真(一般不少于10次)进行综合比较.

1 事故仿真

对于具有事故率为P0(车公里事故率)的路段，其发生交通事故的次数符合二项分布[4]，即

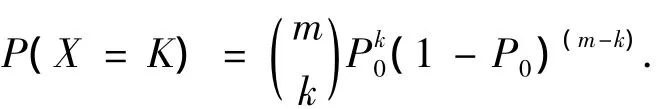
其中:k为发生的事故次数;m为道路上累计作用的交通量(车公里);P0为路网或某类道路的平均事故率(车公里事故率).

对于一段较长公路而言，各路段的道路设计指标和周边环境有所差异，各路段的事故率也各不相同，事故率高的路段往往表明该路段存在缺陷.因此，在分析不同路段上一定累计作用交通量的事故发生次数概率时，应该采用该路段的事故率，其期望值可以从多年运营的道路事故频数进行估计.而进行事故次数仿真时，该路段的事故发生次数符合其对应事故率的贝努利实验.

对于一条100 km长的高速公路，采用传统方法进行分段，以1 km为一个单元，把公路分为100段，以沪杭高速公路浙江段2005年至2009年的下行方向事故数据为基础对每个路段取一个合适的事故率，如图1所示.运用数理统计的原理，在Matlab中运用binornd函数对每个路段随机产生一系列的事故数据，可以把这些事故次数看作是每个路段在对应统计年限内发生的事故次数.函数中累计交通量的不同代表事故统计年限的变化，统计年限越长，对应在路段上累计交通量就越大.3类典型统计时间分别定义为统计年限短(累计交通量取106)，统计年限适中(累计交通量取5×106)，统计年限长(累计交通量取5×107)，按照高速公路单向平均日交通量为2.5×104计算，分别相当于1.5个月，7个月，5.5 a交通量.每类统计年限，随机产生10×100=1 000个事故数.

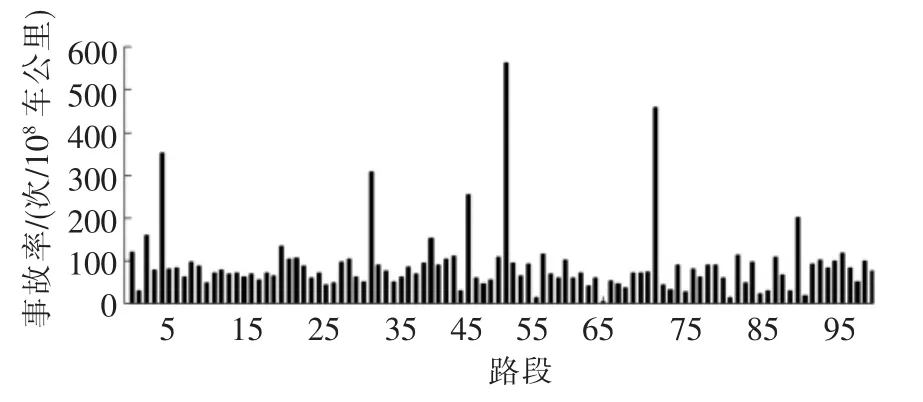
图1 路段事故率

2 双曲正切函数拟合分析

根据《道路交通事故多发位置认定方法(征求意见稿)》，对随机仿真产生的事故数据进行分析，可绘制累计频率散点图.从散点图的形状方面进行分析，当事故统计时间较短时，累计频率散点呈凸形，这与双指数函数形状比较接近，而当事故数据统计时间很长时，累计频率散点呈现S型，而且具备明显的渐进线，这与双指数函数的形状有一定的差异.为了完善累计频率法，可以考虑选取与累计频率散点图变化趋势近似的曲线作为拟合公式.考察双曲正切函数y=a+b×tanh(cx+cd)的特点，通过平移和缩放该曲线，在[0，1]区间内可以产生不同的形状，可较好适应不同条件下的累计频率散点拟合.图2为不同统计年限下事故黑点累计频率曲线散点图与双曲线正切拟合.图3为事故统计年限很长时双指数函数与双曲正切函数拟合的对比分析.

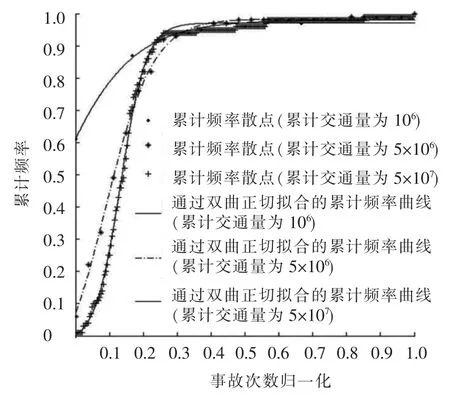
图2 累计频率曲线散点图与双曲正切拟合

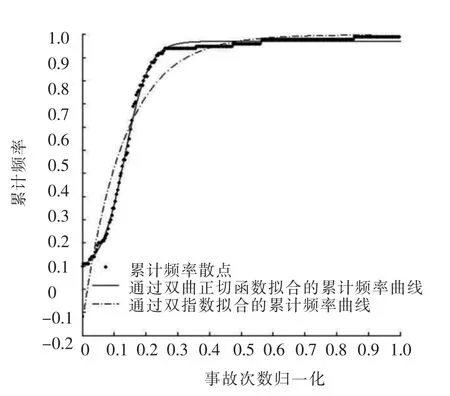
图3 累计频率拟合曲线对比图

不难发现，双曲正切函数能较好适应不同事故统计年限下的累计频率曲线拟合，尤其对于统计年限较长的情况相对双指数函数来讲具有更好的适应性.

表1分别是3种不同交通年限下10次仿真后对累计频率曲线采用双曲正切函数拟合的参数统计结果.

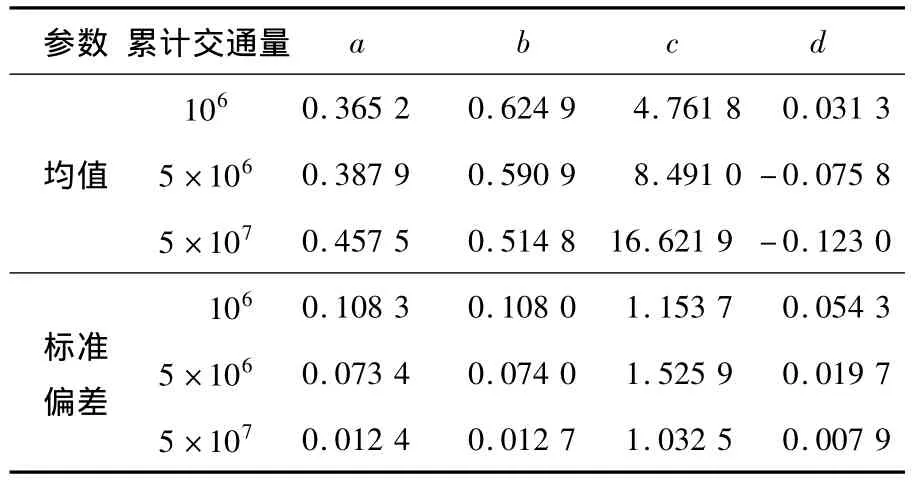
表1 双曲正切函数拟合参数统计结果

分析可知:累计交通量越大(对应事故数据统计年限越长)，a越大，b越小，c越大，d越小;当累计交通量小时，d值为正，当累计交通量适中时，d的符号不确定，当累计交通量大时，d值为负，d的正负可以反映事故数据的大概统计年限;统计年限越长，参数的相对标准偏差越小，说明黑点鉴别越稳定.

3 黑点鉴别方法有效性分析

为了分析双指数函数与双曲正切曲线拟合鉴别的差异性，将不同统计年限下的10次仿真数据产生的累计频率分别按不同的拟合公式进行拟合，求出拟合曲线上的最小曲率半径的位置作为事故黑点鉴别的临界值，并根据该临界值查找出相应的事故黑点的位置，与期望黑点位置进行比较.

期望黑点域表示真实的黑点位置.理论上，对于当道路上的累计交通量无穷大时，各路段发生的事故次数与其事故率成正比.为了便于分析，将各路段事故率×107作为路段的事故发生次数，并在整数区间进行累计频率计算和黑点鉴别.由于采用双指数函数拟合鉴别出的期望事故黑点数是6个，而采用双曲正切函数鉴别出来的结果是8个，综合两者，取期望事故黑点个数取7个，分别对应的路段是 K51+000，K71+000，K5+000，K33+000，K46+000，K90+000 和 K3+000.若鉴别出来的事故位置个数在期望位置域中比重高，则表示检测有效性高，如果检测的位置不在期望域中，则代表误检情况.应该说明的是，误检情况发生不仅受检测方法的影响，同时也受随机数产生的影响，但是从统计的角度对比分析，仍能准确评价检测方法的有效性.

表2为双指数函数和双曲正切函数拟合的鉴别结果.对上述事故黑点鉴别结果提取出检出率和误检率，并作进一步的统计分析，如表3所示.

对比不同累计交通量下事故黑点鉴别结果可以发现:随着累计交通量的增长，2种方法对事故黑点的检出率均有不同程度的增加，但增加并不显著;而交通量对误检率的影响非常显著，在累计交通量小时，事故黑点的误检率非常高，甚至大于70%.这是因为尽管各路段的事故率有所差异，但交通事故的真实发生具有随机性，当事故累计交通量不大时，路段发生的事故次数较少，该随机数的方差与期望值的比值较大，故而各路段真实事故率表现不充分，误检率较高.当累计作用交通量增大，对应的事故次数增加，该随机数的方差与期望值的比值降低，各路段真实事故率表现充分，误检率迅速降低.由于累计频率曲线法是以较长范围路段实际发生的事故为统计依据，是一种事后检测方法而非预测法，因此在实际操作中若有控制误检率，应给出相应的事故次数.根据以实际事故数据为基础的仿真分析，若以误检率20%左右控制，相当于5×106累计交通量下产生的事故次数，对应的全路段的平均每公里的发生的事故次数约为4～5次，这对沪杭高速公路来说相当于7个月的统计时间.对于交通量小或者平均事故率很低的道路，为获得较低的误检率，必须有较长的统计年限的事故数据为基础，使各路段的事故率表达充分.对比2种函数的累计频率曲线拟合黑点鉴别结果可以得出:

1)在较低累计交通量下2种函数拟合的效果差别性不大，相关系数都较高.随着交通量的增大，双指数函数的拟合相关性有所降低，尤其是在曲率最大位置(黑点判别临界值)与实际情况相差较大(见图3)，而双曲正切函数仍然保持很高的相关性，曲线拟合效果也好.

2)双曲正切函数在事故黑点的检出率上稍高于双指数函数，在误检率上略差于后者.这是因为两者各自的期望事故黑点数有所差异，前者高于后者，而为了比较本文采用了两者的平均值作为真实期望值.值得一提的是，双曲正切函数拟合对于大累计交通量的情况下拟合相关性要显著高于后者，理论上将前者期望值作为真实期望值更为合理，这时双曲正切函数的误检率将能显著提高，而双指数函数的检出率将明显降低.

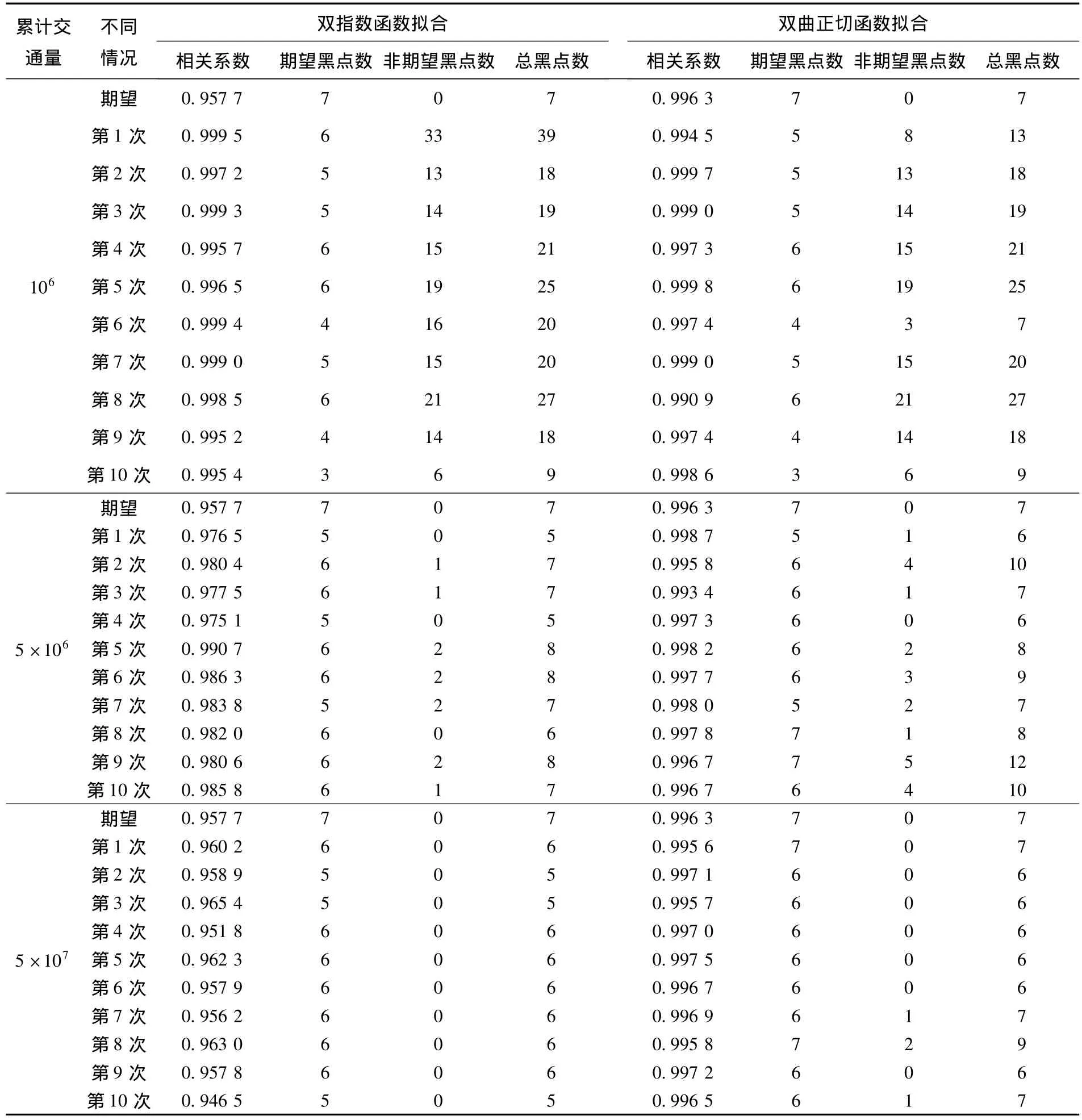
表2 双指数函数拟合黑点鉴别结果

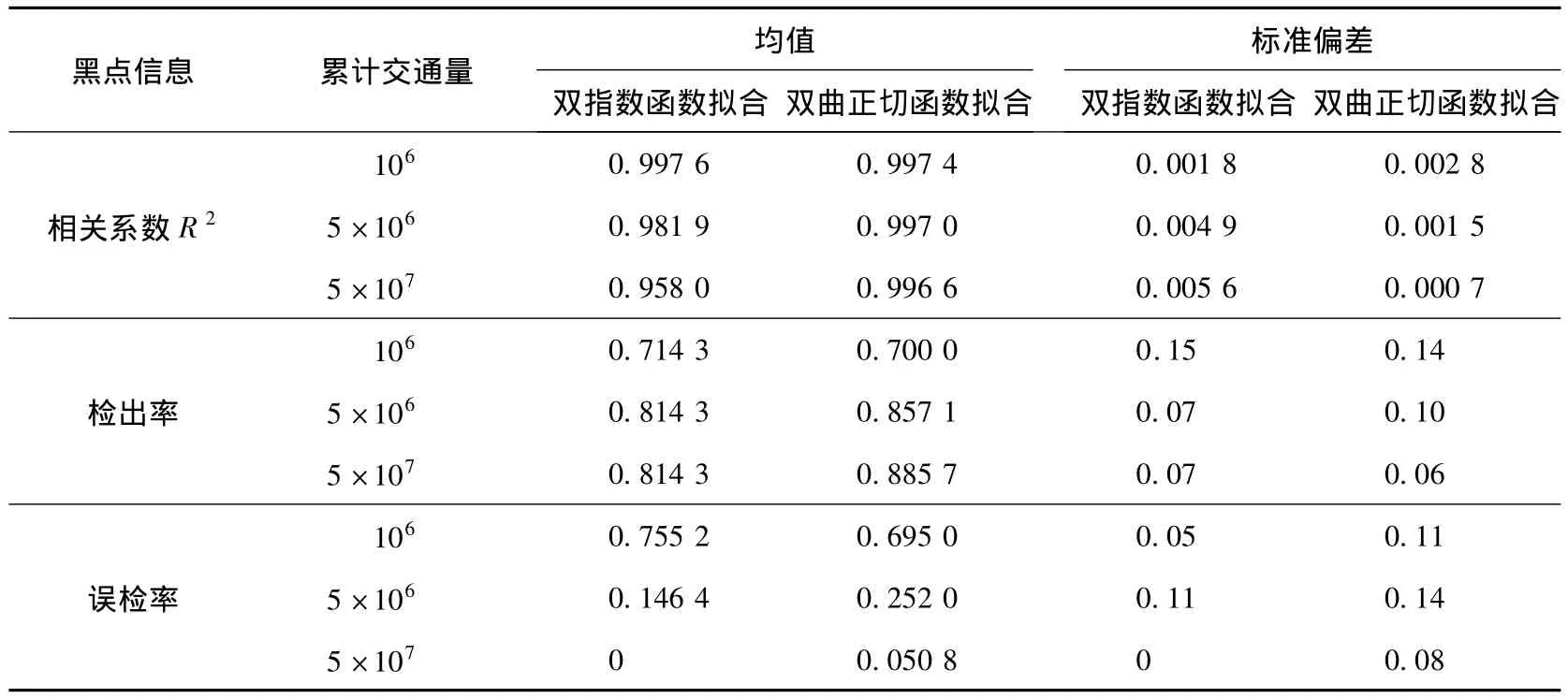
表3 2种拟合函数检出率和误检率对比和分析

4 应用分析

以沪杭高速公路的上行方向嘉兴段事故数据为基础，应用双曲正切函数对累计频率曲线进行拟合和事故黑点鉴别分析，为比较不同年限的事故黑点鉴别结果，分别在2004年12月21至2008年6月20的事故数据抽取0.25、1、3.5 a的事故数据进行应用分析，曲线拟合情况如图4所示.

求出拟合曲线上的最小曲率半径的位置作为事故黑点鉴别的临界值，该临界值对应的黑点的事故临界次数分别为6次、18次和76次.根据事故黑点的临界次数，分别鉴定出的事故黑点位置如表4所示.

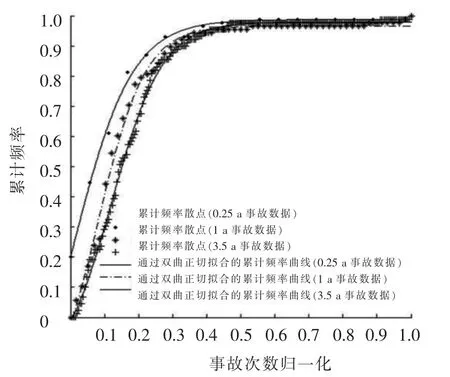
图4 不同累计交通量作用下累计频率曲线散点图与双曲正切拟合

表4 不同累计交通量作用下事故黑点鉴别结果

可见，不同累计交通量作用年限下的事故黑点鉴别结果有一定差异性，根据前面的分析可以推断0.25 a事故黑点鉴别结果可靠性最低，3.5 a的事故黑点鉴别结果可靠性最高，1 a的事故黑点鉴别结果非常接近3.5 a的，具有较高的可靠性，其误检率低于20%，在一定程度上验证了前面的结论.从事故鉴别的结果看，各事故黑点的特征如下:K75+000为大云主线收费站出口;K76+000为大云收费站主线入口;K99+000为沪杭高速与乍嘉苏高速的互通立交;K109+000段为嘉兴服务区;K117+000为桐乡屠甸出口;K135+000为长安服务区，K138+000为长安出口.

其中K99+000处的事故次数达到了216次，其次是K109+000处，事故次数达到194次，显著高于其他路段.可见，对于平原区高速公路，事故黑点位置主要发生在互通立交(特别是枢纽型互通)出入口，服务区出入口和主线收费站出入口等位置.

该方法同样可用于一般等级公路或者其他地区高速公路，对改造前为山区二级公路的104国道上虞段K1545—K1569(1995年1月—1997年12月数据)，原太高速公路K0—K95(2001年2月—2003年9月数据)，汉宜高速公路荆州段K128—K226(1995年—1999年数据)，太旧高速公路寿阳—旧关段K446—K508(2001年1月—2003年9月数据)进行黑点鉴别分析，双曲正切函数曲线拟合情况如图5所示，黑点鉴别结果如表5所示.

从表5可知，无论何种情况下，双曲正切拟合相关系数R2都很高，对于不同的累计交通量具有很好的适应性.另外统计年限内汉宜高速荆州段上、下行方向的全路段每公里事故数都超过4次的最低要求，拟合曲线表现出一定的S形，事故黑点鉴别的误检率控制在20%左右.104国道上虞段的全路段每公里事故数接近4次，拟合曲线表现出向S形转变的趋势，事故黑点鉴别的误检率具有一定的保证.而原太高速上、下行方向，太旧高速寿阳—旧关段上、下行方向的全路段平均每公里事故次数都明显小于4次的最低要求，所以为获得较低的误检率，必须要有更长统计年限的事故数据为基础.

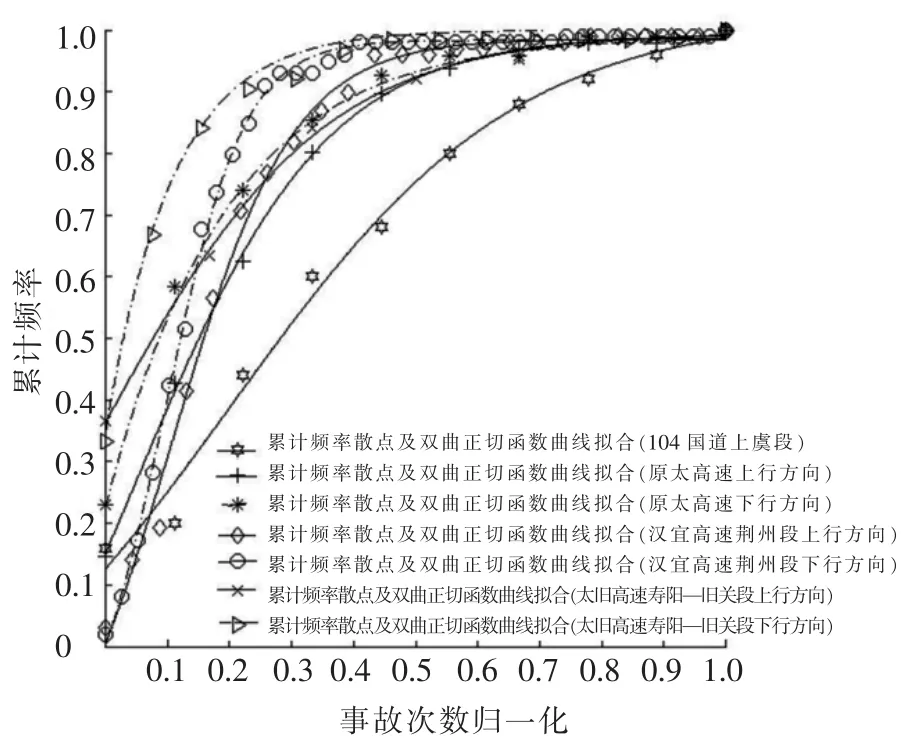
图5 累计频率曲线散点图与双曲正切拟合

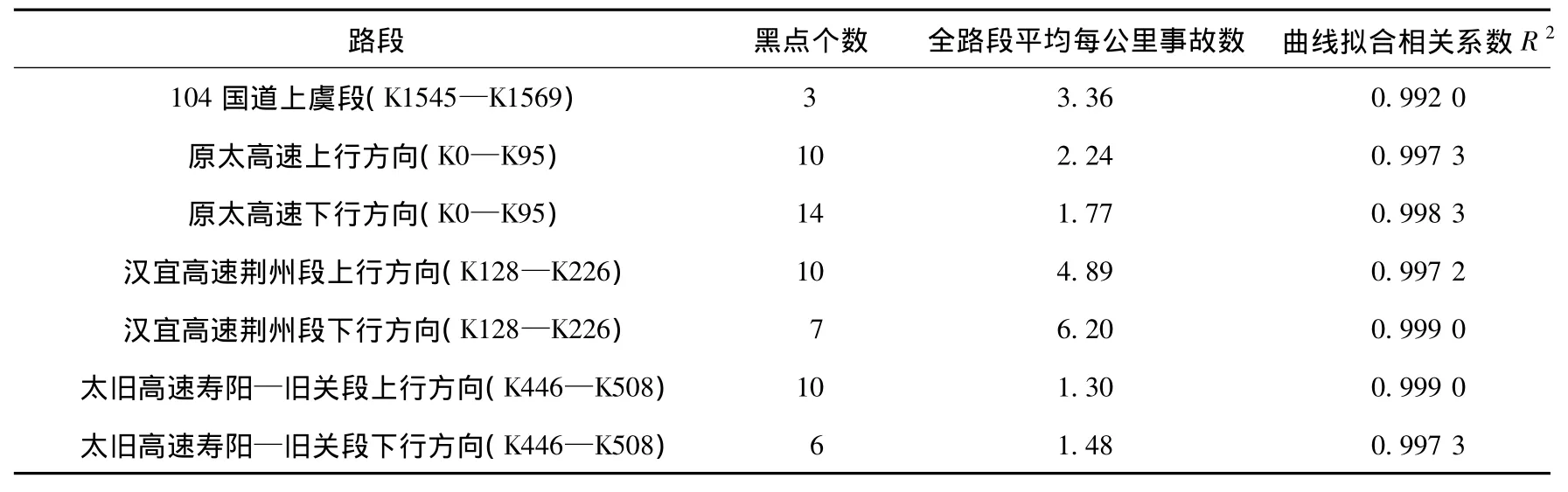
表5 黑点鉴别结果

5 结论

1)双曲正切函数和双指数函数在累计频率曲线拟合的相关性方面前者要优于后者，并且对于不同的累计交通量具有很好的适应性.同时，在黑点的检出率方面前者也具备一定的优势，因此双曲正切函数可替代双指数函数进行事故黑点鉴别.

2)一定事故率下统计年限对事故黑点的误检率有非常重要的影响，当统计年限较低时，事故黑点的误检率非常高，甚至超过50%.为将误检率控制在20%左右，建议待鉴别道路的平均每公里事故次数不小于4次.

[1]ROBERT R V，VEERARAGAVAN A.Hazard rating scores for prioritization of accident prone sections on highways[J].Transportation Research Record:Journal of the Transportation Research Board，2004，1878:143－151.

[2]TARKO A P，KANODIA M.Effective and fair identification of hazardous locations[J].Transportation Research Record:Journal of the Transportation Research Board，2004，1897:64－70.

[3]ELVIK R.New approach to accident analysis for hazardous road locations[J].Transportation Research Record:Journal of the Transportation Research Board，2003，1953:50－55.

[4]肖慎，过秀成，宋俊敏.公路交通事故黑点诊断技术研究[J].公路交通科技，2003，20(4):95 －97.

[5]裴玉龙，丁建梅.鉴别道路交通事故多发点的突出因素法[J].中国公路学报，2005，18(3):99 －103.

[6]孟祥海，盛洪飞，陈天恩.事故多发点鉴别本质及基于BP神经网络的鉴别方法研究[J].公路交通科技，2008(03):124－129.

[7]杨轸，方守恩，高国武.事故多发路段的研究[J].上海公路，2000(04):5－8.

[8]方守恩，郭忠印，杨轸.公路交通事故多发位置鉴别新方法[J].交通运输工程学报，2001，1(1):90 －94.