基于Tobit回归的山区高速公路事故率分析模型

孟祥海，刘振博,2

(1.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090；2.四川省国土空间规划研究院)

1 前言

在传统的交通事故分析模型或预测模型中，使用的因变量多为事故次数、伤亡事故次数或事故伤亡人数等离散型的随机变量，并采用泊松分布、负二项分布、零堆积泊松分布或零堆积负二项分布等对离散型的事故数据进行拟合。马壮林等针对交通事故多发路段，建立了事故次数的泊松回归模型、负二项回归模型及零堆积回归模型；孟祥海等建立了线形与交通状态组合条件下的追尾事故次数负二项分布模型；依据负二项分布标定了高速公路基本路段事故次数预测模型，提出了基于负二项分布的路段安全性评价方法；基于统计及假设检验，深入分析了事故次数、伤亡事故数、事故死亡人数等离散型事故数据的统计分布特征。

然而在实际应用中，由于交通事故数据的隐私性和敏感性，往往很难直接获得事故次数、事故伤亡人数等数据，尤其是发生在具体道路上的上述数据。相反，在许多交通事故分析报告、交通安全评价报告甚至是交通安全研究报告中，亿车公里事故率、百万辆车事故率等事故率指标经常被用来作为评价指标，用以描述道路交通安全状况。也就是说，在有些没有事故次数、伤亡人数等事故绝对指标的情况下，事故率即成为可获取的事故指标。因此，在此背景下，基于事故率来建立事故分析模型或预测模型就具有了一定的现实意义。另外，事故率本身就包含了交通量、路段长度等事故关联因素信息，是非常有效和客观的交通安全评价指标。

从统计学原理上看，事故次数作为因变量，只能取非负整数，属于离散型随机变量，因此，采用泊松回归或负二项回归来建立事故分析模型是合理的。当统计期短或路段划分较短时，事故次数统计数据中可能会出现大量的“0”值，此时，还可考虑采用零堆积泊松回归或零堆积负二项回归来建立事故分析模型。不同于事故次数，事故率属于连续型的随机变量，泊松、负二项及零堆积类回归方法已不再适用，需要有新的回归方法。同理，当统计期短或路段划分较短时，事故率统计数据中仍可能出现大量的“0”值，此时，事故率取值是受限的，属于受限因变量。

一般而言，连续型受限因变量的回归方法常采用Truncated回归(断尾回归)和Tobit回归(截取回归)两种。其中，断尾回归适用于统计数据能取得全体样本，而只有在大于或小于某个常数才能被观测到的情况；Tobit回归适用于当统计数据大于等于或小于等于某个常数时，所有的数据均被记录为这个常数的情况。Tobit回归虽然可以取得全部的观测数据，但对于某些观测数据，因变量取值被压缩到一个点上了，此时，因变量的概率分布就变成了由一个离散点和一个连续分布所组成的混合分布。因此，当事故率属于受限因变量时，采用Tobit回归来建立事故分析模型是适合的。

鉴于中国尚未将Tobit模型应用于道路交通安全领域的实际情况，该文尝试应用Tobit回归来建立山区高速公路事故率与几何线形条件之间的关系模型，旨在验证Tobit模型的适用性问题，并据此分析几何线形条件对交通事故的影响。山区高速公路复杂的几何线形条件，是诱发交通事故的重要原因之一，从事故率角度进一步分析这种影响关系也是十分有意义的。

2 事故率分析模型建模及求解方法

2.1 事故率分析模型形式

事故率分析模型是一个描述事故率指标与事故影响因素之间相关关系的多元线性回归模型，即：

Yi=βXi+εi,i=1,2,…,N

(1)

式中：Yi为路段i上的事故率；Xi为路段i上的事故影响因素；β为待估计的参数变量；εi为残差项；N为路段数(即样本数)。

2.2 回归方法选择

针对式(1)的多元线性回归模型，由于事故率是连续型受限因变量，因此，可采用断尾回归和Tobit回归两种方法来建立事故率分析模型。

对于断尾回归，设样本总体Y原来的概率密度为f(Y)，则断尾后的概率密度f*(Y)为：

(2)

式中：P(Y>0)为事故率Y>0的概率。

当事故率为“0”时，断尾回归认为断尾处概率密度为“0”，即在断尾回归中事故率为“0”的情况不会出现，显然，这与事实是不符的。

对于Tobit回归，受限因变量的概率密度分布被变换成由一个离散点和一个连续分布所组成的混合分布。Tobit回归认为，在左侧受限处的概率密度不为“0”，即事故率为“0”的情况可能会出现，这更符合事故率数据的实际情况。事实上，此时应用Tobit回归，可看做求解事故率的最优解问题：在交通事故不发生的情况下，事故率的最优解即为边角解(Corner solution)，即事故率为“0”；在交通事故发生的情况下，则事故率一定为正数。

应用Tobit回归建立事故率分析模型可表达为：

(3)

(4)

2.3 事故率分析模型参数求解方法

应用Tobit回归时，如果用最小二乘法(OLS)进行估计，非线性项将被纳入残差项中，无论使用整体样本还是去掉离散点后的子样本，都不能得到一致的估计。

若采用去掉离散点后的子样本，即使用“Yi>0”的子样本进行OLS参数估计时，可求得事故率均值E(Yi)为：

E(Yi|Xi;Yi>0)=βXi+σ·λ(-βXi/σ)

(5)

式中：λ为逆米尔斯比率(IMR)；对任意常数α，λ(α)=φ(α)/[1-Φ(α)]，其中Φ(α)为标准正态分布的分布函数，φ(α)为标准正态分布的概率密度函数。

在使用子样本进行回归时，由于忽略了非线性项σ·λ(-βXi/σ)，该项被纳入到了残差项中，从而导致残差项与Xi相关，OLS无法得到一致的估计。

若使用整体样本进行OLS参数估计时，可求得事故率均值E(Yi)为：

E(Yi|Xi)=E(Yi|Xi;Yi>0)·P(Yi>0|Xi)=Φ(βXi/σ)[βXi+σ·λ(-βXi/σ)]

(6)

因此，使用整体样本进行OLS参数估计时，也将非线性项纳入到残差项中，从而不能得到一致的估计。

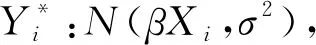
(7)

(8)

此时，式(4)中Yi的概率密度函数为：

(9)

其中，1(·)为示性函数，即如果括号里的表达为真，取值为1；反之，取值为0。得出样本整体的似然函数为：

(10)

(11)

对式(11)求令其最大化的解，即可得到模型参数估计结果。由于这是一个复杂的非线性问题，可考虑采用迭代法进行求解，例如采用牛顿迭代法等求解。

3 数据来源与数据处理

3.1 数据来源

依托广东省交通运输厅科技项目“基于全社会成本的高速公路设计方案评价技术研究”(2012-01-001-02)科研课题，收集到了京珠高速公路粤北段2006年1月至2009年6月发生的1 557起事故数据、粤赣高速公路2007年1月至2012年7月发生的1 678起事故数据以及上述两条高速公路的几何线形数据。京珠高速公路粤北段为山岭重丘区高速公路，设计速度100 km/h(局部路段80 km/h)，双向四车道，全长109.29 km。粤赣高速公路为重丘区高速公路，双向四车道，设计速度100 km/h，全长136.1 km。

3.2 路段划分

由于该文建立的事故率分析模型主要是基于公路几何线形条件，因此，应基于几何线形条件对上述两条高速公路进行路段划分。平面线形划分为直线路段和平曲线路段两类。竖曲线的划分是以变坡点为界，划分为竖曲线前半段和后半段，若前半段或后半段的切线纵坡为上坡，则该半段竖曲线归类为竖曲线上坡段，反之归类为竖曲线下坡段。将平纵线形进行组合，可得到以下8种路段：直线-上坡路段、直线-下坡路段、直线-竖曲线上坡路段、直线-竖曲线下坡路段、平曲线-上坡路段、平曲线-下坡路段、平曲线-竖曲线上坡路段、平曲线-竖曲线下坡路段，编号分别为路段类型1～8。路段划分结果如表1所示，京珠高速公路粤北段共划分出1 082个路段，粤赣高速公路共划分出1 242个路段，这些路段就是建立事故率分析模型的样本。

表1 路段划分结果

3.3 事故率计算与异常值处理

对划分后的路段，进行事故率指标计算。事故率选用亿车公里事故率，计算公式如下：

(12)

式中:Rj为路段j上的事故率[次/(亿车·km)]；Aij为路段j上第i年的事故次数(次)；AADTij为路段j上第i年的年平均日交通量(pcu/d)；Lj为路段j的长度(km)；n为统计年限，对于不足一整年的数据，须折算。

对因路段划分长短不同所导致的亿车公里事故率异常值(主要是因路段过短而出现的极高的事故率值)，以及过长或过短的路段，应进行处理。为此，对路段长度及亿车公里事故率进行缩尾处理，剔除上下各1%的路段长度极端值和1%高的事故率极端值。最终得到了2 239个有效路段(表2)。其中，京珠高速公路粤北段有效路段1 033个，粤赣高速公路1 206个。

由表2可知：事故率为“0”的路段数所占比例较大，达到了路段总数的47.5%。这表明：亿车公里事故率是受限因变量(含“0”值较多的连续型变量)，因此，采用受限因变量的回归方法来建立事故率分析模型是合理的。

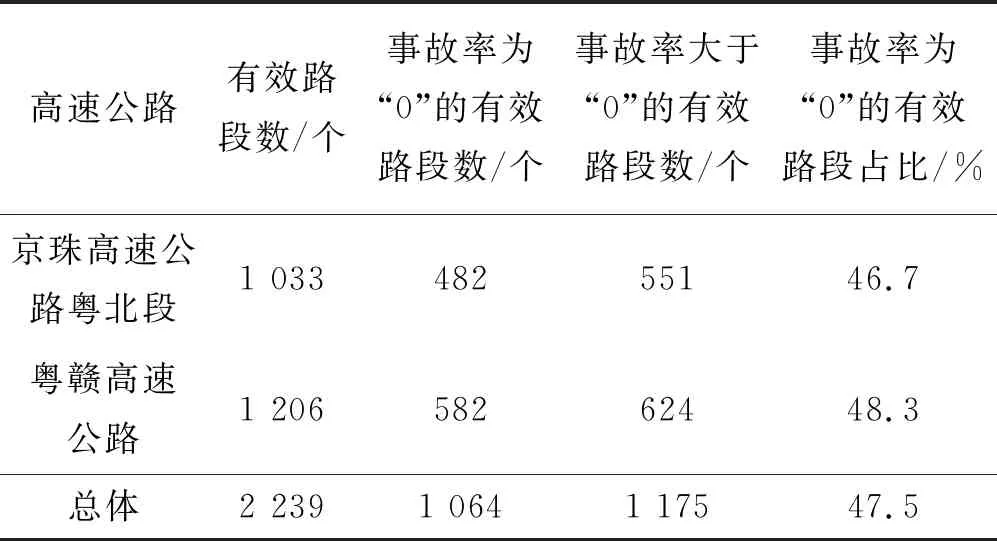
表2 有效路段及事故率

3.4 数据分析

剔除异常值后，有效路段上的事故率及其线形数据、交通量数据统计结果见表3。不同类型路段上的事故率统计结果见表4。由表4可知：下坡路段事故率整体高于上坡路段，事故率平均值较大的是直线-下坡路段和直线-竖曲线下坡段，事故率平均值较小的是平曲线-上坡路段和直线-上坡路段。

4 事故率分析模型自变量及其赋值

山区高速公路事故率分析模型中选取的因变量为亿车公里事故率(R)；选取的自变量为年平均日交通量(AADT)、路段长度(L)、平曲线曲率(DH)、竖曲线曲率(DV)、纵坡类型(ID)和纵坡坡度(i)，单位分别为pcu/d、m、km-1、km-1、无量纲和%。

表3 事故率及道路线形数据统计结果

表4 不同类型路段事故率数据统计

其中，纵坡类型变量取“0”或“1”值，属于虚拟变量，用以区分上下坡路段，上坡路段取“0”，下坡路段取“1”。选择平曲线曲率和竖曲线曲率的原因是，可方便变量的赋值。路段类型1～4均为平面直线与纵断面线形组合路段，此时平曲线半径为无限大，而平曲线曲率则可取为“0”值。同理，在纵坡与平面线形组合的路段中，纵坡路段的竖曲线半径为无限大，而竖曲线曲率则可取为“0”。由于在路段划分中，上、下坡路段已分属不同的路段类型，因此，纵坡坡度均取绝对值。线形指标原始数据与赋值后的数据示例，见表5。

5 事故率分析模型参数标定与分析

5.1 模型参数标定

为横向比较不同自变量对事故率的影响程度，需要消除各自变量特征尺度的潜在影响，因此，需要对自变量数据进行归一化处理。归一化公式为：

(13)

模型的因变量，即亿车公里事故率，也应进行归一化处理，公式同式(13)。

对归一化后的事故率及事故影响因素数据，应用Stata统计分析软件进行参数标定，结果见表6。

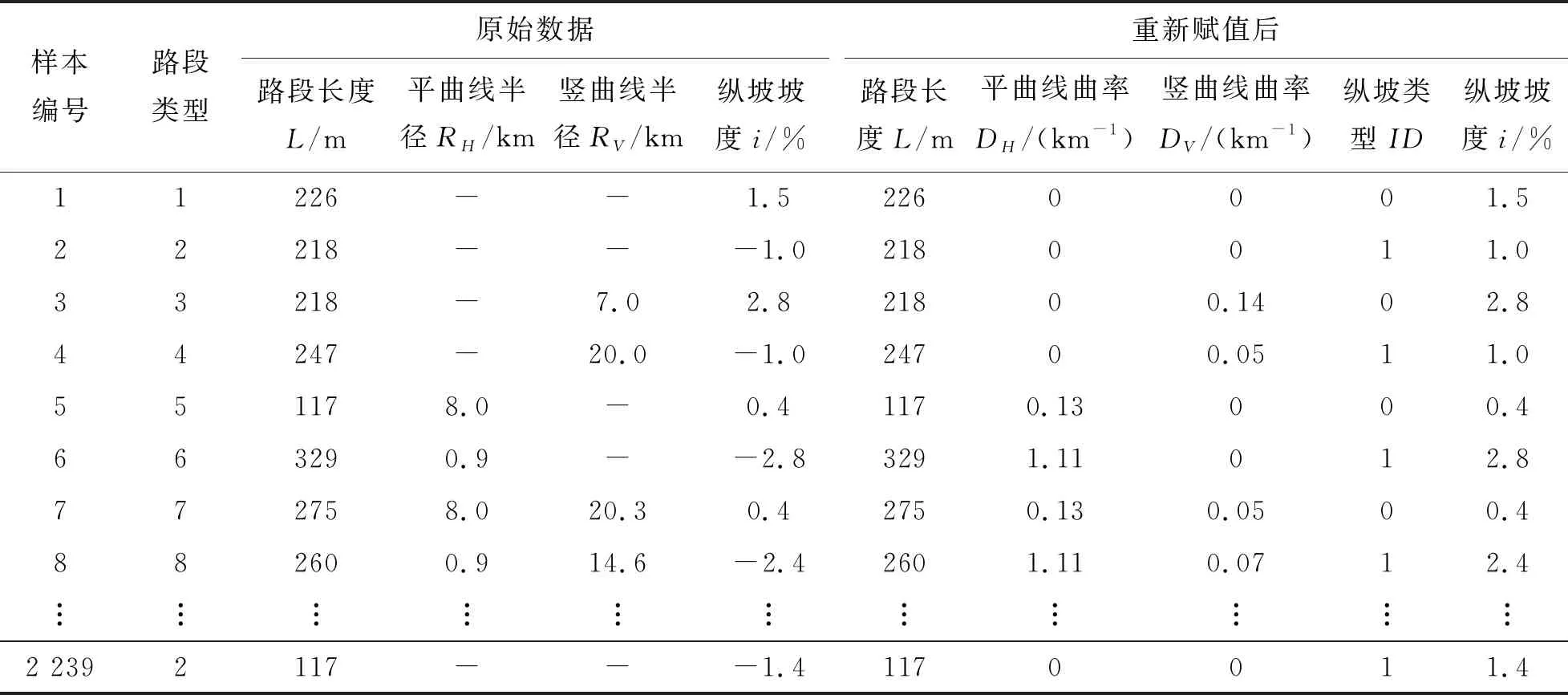
表5 线形指标原始数据与赋值后数据对比示例

注：“-”为原始数据空值项。

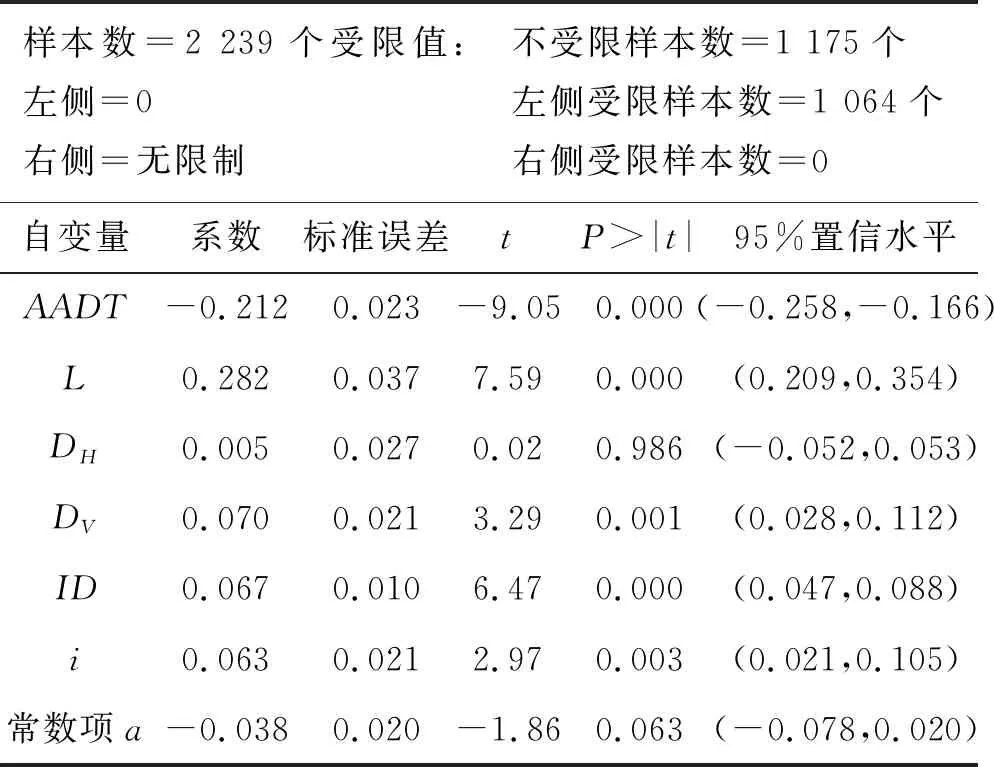
表6 模型参数标定结果

事实上，由于基于Tobit回归的山区高速公路事故率分析模型属于广义线性模型，模型的回归系数并不能直接代表自变量对因变量的影响程度大小，因此还需对模型自变量求其各自的边际效应。边际效应的计算结果如表7所示。

表7 自变量边际效应计算结果

5.2 模型结果分析

由表6可知：在标定模型的2 239组数据中，非受限数据1 175组，以“0”值作为左侧受限界限的左侧受限数据1 064组。除平曲线曲率显著性较差外，年平均日交通量、路段长度、竖曲线曲率、纵坡类型、纵坡坡度绝对值在95%置信水平下均是显著的，概率值P均小于0.05。

由表7可知：年平均日交通量的边际效应为负，说明随着年平均日交通量的增加，亿车公里事故率逐渐减小。这也隐含着说明：事故次数随交通量的增长不是线性增加的，即事故次数的增长率要低于交通量的增长率。路段长度的边际效应为正，说明随着路段长度的增加，亿车公里事故率在增加。平曲线曲率对事故率的影响不明显，边际效应极小。竖曲线曲率的边际效应为正，说明随着竖曲线曲率的增大，即竖曲线半径的减小，亿车公里事故率在增大，该回归结果与竖曲线半径越大交通安全状况越好的相关研究结论是相符的。纵坡类型及纵坡绝对值的边际效应均为正，说明下坡路段亿车公里事故率要高于上坡路段，且随着纵坡坡度绝对值的增长，亿车公里事故率也随之增加。这一回归结果也证实了下坡路段危险性高于上坡路段、坡度越大危险性越大的相关研究结论。

对事故率影响最大的因素是纵坡坡度，最小的是竖曲线曲率。记竖曲线曲率对亿车公里事故率的影响程度为1.0，则年平均日交通量、路段长度、纵坡坡度、纵坡类型对亿车公里事故率的影响程度分别为3.1、4.1、9.1、9.7。

6 结论及有待进一步研究的问题

6.1 结论

(1) 由于事故率是连续型随机变量，加之会出现大量“0”值的情况，因此，采用Tobit回归来建立事故率分析模型是适宜的。

(2) 基于Tobit回归建立的山区高速公路事故率分析模型，较好地反映出了年平均日交通量、几何线形条件等对事故率的影响。模型标定结果及边际效应数值表明，纵坡类型对事故率的影响最大；其次依次是纵坡坡度、路段长度、年平均日交通量和竖曲线曲率。

6.2 有待进一步研究的问题

(1) 该文所建立的事故率分析模型，仅考虑了交通量、路段长度以及几何线形条件等对交通事故的影响，在后续的研究中，还应进一步考虑路面条件、天气条件以及交通状态等对交通事故的影响，从而提高分析模型的精度。

(2) 该文仅考虑了交通安全中“量”的问题，即事故率。在后续的研究中，还应考虑事故严重程度指标，如伤亡事故率等，这是交通安全中“质”的问题。