基于AGA-SVM公路软基沉降预测

张健明，唐仁华，毛凤山，丁明发

(1.中交一公局桥隧工程有限公司，湖南 长沙 410000；2.长沙学院 土木工程学院；3.湖南大学 土木工程学院 )

公路沉降是威胁公路安全建设与运营的主要难点，正确的沉降数据能够为施工提供指导，同时也是道路安全运营的前提之一。目前，道路沉降预测的方法有很多种，基本上可分为以各种函数为模型的静态的曲线拟合法和以计算机技术为基础的动态智能预测法。苗胜军等指出双曲线法对预测应力-应变关系明显呈非线性的高压缩性软黏土较为适合；宰金珉、梅国雄提出的Logistic 模型在粉土及砂类土层地基中对沉降预测效果较好；肖治宇，陈昌富将Richards模型应用到软土路基的沉降预测中；张立萍使用两种指数曲线函数在公路地基沉降预测中进行了对比计算；涂许杭等对双参数指数的威布尔模型进行改进，提出了预测沉降的修正威布尔曲线模型。此外，还有一些学者提出了星野模型、对数抛物线模型、Asaoka图解等模型。以上众多曲线拟合方法均需要假设沉降曲线满足特定的函数关系，而实际的路基沉降曲线通常不符合单一的曲线形态，且其中函数的参数影响因素较多，因此这种静态预测方法不可避免地存在一定误差。随着计算机技术特别是人工智能的迅速发展，对沉降进行动态预测成为研究热点，计算时引入了灰色系统、神经网络、遗传算法、支持向量机等众多智能算法以及由两种方法组合而成的混合智能算法。其中人工神经网络具有很强的自组织、自学习能力及非线性数据处理能力，曾被广泛运用于路基沉降预测。但它也存在过度拟合的情况，噪声对数据的影响很大，算法泛化能力差，精度较差。而支持向量机以其优异的非线性拟合及泛化能力，能很好地排除沉降观测数据的噪声干扰，具有相对较高的精度，但是，其沉降预测精度依赖于参数C、σ、ε的取值。

因此，该文选择自适应遗传优化的支持向量机参数C、σ、ε，建立自适应遗传算法支持向量机沉降预测模型，并将此模型应用于兴汕高速公路软基沉降预测。

1 支持向量机沉降预测基本原理

支持向量机(SVM，Surpport Vector Machine)是一种基于有限样本的统计学习方法，通过构造超平面，使得分类间隔最大化，如图1所示。SVM方法根据结构化风险最小的准则，尽量提高学习机的泛化能力，较好地解决了小样本、非线性、高维数、局部极小值等实际问题。另外，SVM是一个凸二次优化问题，能够保证找到的最优解是全局最优解，这些优点使得支持向量机可以用来处理高度非线性的沉降数据并进行预测。

将现场实测路基沉降数据{(x1,y1),…,(xi,yi),…,(xl,yl)}作为训练样本，其中xi为影响因素，yi为沉降观测值。训练样本代入预测模型中，可以求解预测模型参数，沉降拟合值可以用式(1)的决策函数来计算：

y=ω·x+b

(1)

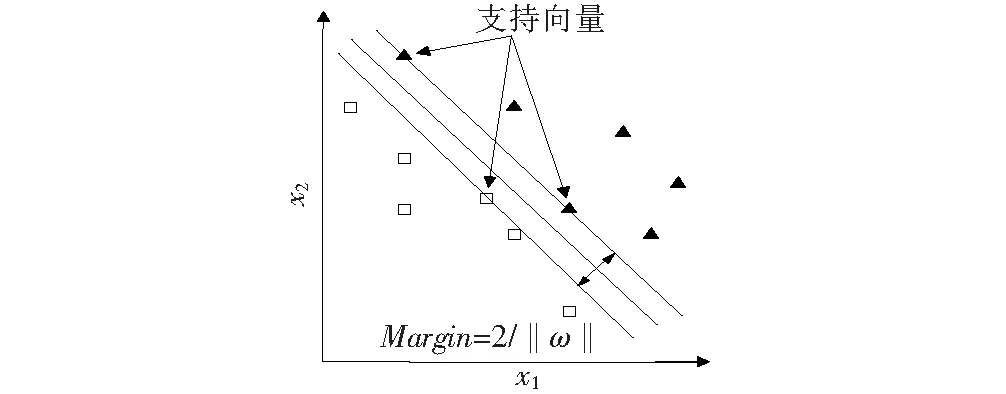
图1 支持向量机最优分类面原理

考虑到沉降观测数据具有噪声干扰，引入不敏感带损失函数ε，假定所有的样本到回归函数的距离都小于ε，决策函数的求解可以转化为一个二次规划问题：

(2)

为了提高模型的泛化能力，引入松弛因子ξ和ξ*(ξ、ξ*分别对应样本点在拟合函数的上方和下方两种情形)，式(2)的二次规划问题可以写成式(3)形式：

(3)

式中：C为一正常数，称为惩罚因子，松弛因子ξ和ξ*分别对应样本数据点在回归曲线上方和下方两种情形。

通过建立拉格朗日方程求解式(3)，式(3)的不等式方程组约束优化问题可以转化为等式约束下的函数最小值问题，即：

(4)

求解式(4)后得到沉降非线性回归函数表达式为：

(5)

由于沉降影响因素与沉降值呈高度非线性关系，通过引入核函数把低维样本数据映射到高维特征空间中，该文选择式(6)所示的径向基核函数为核函数，并用K(xi，xj)替换式(4)中(xi，xj)。

(6)

由此得到沉降非线性回归函数的表达式为：

(7)

得到式(7)后，将任一沉降影响因素xi代入式(7)中，即可实现支持向量机沉降拟合和预测功能。

式(4)的求解需要先确定惩罚因子C和核函数中的参数σ及分类间隔ε，合理的参数取值才能达到较好的沉降拟合精度。为了建立C、σ、ε与沉降拟合精度之间的关系，以沉降拟合值与实测值的平方和作为误差函数，如式(8)：

φ(C，σ，ε)=|y拟合-y实测|2

(8)

提高沉降预测的精度即要求式(8)取最小值，该文选择自适应遗传算法来对式(8)进行寻优。

2 自适应遗传算法支持向量机沉降预测模型

2.1 自适应遗传算法

遗传算法借鉴生物进化“物竞天择，适者生存”思想，利用对变量的编码、初始种群生成、适应度评价、选择、交叉、变异等操作实现对变量最优解的搜索。将选择、交叉、变异过程循环操作能够使种群中的个体最后都适应环境，在算法中表现为，最后的种群大部分都趋近函数的最值。

但是标准的遗传算法存在收敛速度慢及算法早熟的缺点。基于此，该文采用自适应遗传算法(AGA,Adaptive Genetic Algorithm)，通过自适应调整变异概率与交叉概率，使算法保持较快的收敛速度和较高的收敛精度。

2.2 自适应遗传算法支持向量机沉降预测步骤

基于自适应遗传算法的优点，采用该算法对支持向量机模型中C、σ、ε参数寻优，目标函数值使用式(8)计算，寻找最优的C、σ、ε参数值使得函数φ(C，σ，ε)取最小值，此时，自适应遗传算法支持向量机(AGA-SVM)沉降拟合及沉降预测模型精度最高。

该方法中自适应遗传算法支持向量机主要参数为：个体数目为50，其他遗传算法参数取值与文献[14]一致；根据经验，优化参数取值区间为：C=0～500，σ=0～50，ε=0～1；最大迭代次数为100。为了节约计算资源，计算过程中如果达到了收敛条件(迭代10次，最优解没有改善)，也可以提前终止循环。综合考虑支持向量机算法的特点，为了避免过度拟合导致的预测功能的劣化，可以根据最优解的变化大小提前退出迭代，这样能够保证模型在有一定拟合能力的同时具有优良的预测能力。

采用AGA-SVM沉降预测模型的主要步骤为：

(1) 将沉降观测数据中时间t和填土高度h作为自变量，沉降观测值y作为因变量，将数据序列(t，h，y)代入SVM中进行训练。

(2) 利用训练完成的SVM模型计算沉降拟合值y拟合。

(3) 以C、σ、ε为变量，以式(8)为目标函数计算拟合误差，利用AGA对C、σ、ε进行寻优，使得目标函数取最小值，输出最优解。

(4) 将时间与填土高度数据序列(t，h)代入AGA-SVM模型，计算得到沉降拟合值和沉降预测值。

3 工程实例分析

实例工程位于广东兴宁至汕尾区域，地处东南沿海地区，广泛分布着深厚软土，道路建设期间沉降较大，准确的沉降预测数据能够给路堤补偿高度提供参考。工程软土主要为淤泥质粉质黏土，局部为淤泥质砂、腐殖土等淤泥类软土及软塑状黏性土等非淤泥类软土。平原区软土呈面状分布，根据钻探成果及地调资料，T3 合同段主线软土分布总长约4 180 m，占该合同段总长约76%；其中路基、桥台段软土长度约2 812.5 m，占该合同段软基总长约67.3%，占路线总长约51.1%；桥梁段软土长度约1 367.5 m，占该合同段软基总长约32.7%，占路线总长约24.9%。在工程建设期间，在道路沿线关键横断面分别埋设了沉降计、水平位移计监测路基的固结程度和安全状态。其中，沉降计埋设在路堤底部两侧和中心位置，文中选取K14+530断面中心位置进行沉降预测。

该断面区域软土埋深较浅，同时处理接近桥头路段，表1为该断面地层特性。该断面处地基处理方法是素混凝土桩结合袋装砂井提高路基的承载力，袋装砂井在素混凝土施工阶段为路基施工及预压阶段提供路基竖向排水通道，其中，素混凝土采用正方形布置，桩径0.4 m，距间1.7 m，长度8.5 m，桩身设计强度C15；袋装砂井采用正方形布置，砂井直径7 cm，间距1.7 m，长度5.5 m。

将埋设在路基中部的沉降计前面278 d的填土时间、填土高度、监测沉降数据作为输入用于训练SVM模型，以最小拟合误差作为目标函数，利用AGA对C、σ、ε寻优，得到最优的解为C=496.02，σ=1.03，ε=0.01(图2)。从图2可以看出：SVM的拟合效果非常好，同时为了验证模型的正确性，利用训练好的预测模型预测第278、380 d的沉降数据，结果表明：该文方法预测得到的沉降值与实测值较接近。从沉降预测结果(图2)可以分析得到：该断面处沉降在该级荷载下趋于稳定。

表1 K14+530断面地层特性

图2 K14+530断面沉降预测结果

为了体现该文方法的优越性，将BP神经网络沉降预测数据与该文方法进行对比，虽然BP神经网络在沉降拟合阶段精度高于AGA-SVM，但是由于过度拟合导致算法的预测精度较差，对比结果如图2所示，可以看出该文方法对于短期沉降预测精度高于BP神经网络预测精度，利用该文方法能够实现对软土路基短期沉降预测。

4 结论

(1) 建立了基于自适应遗传算法优化的支持向量机沉降预测模型，将该模型应用于工程实践中，与实测数据吻合良好，提出了一种合理有效的沉降预测方法。

(2) 针对同一工程实例，将该文方法与BP神经网络优化算法计算结果进行横向比较，该文自适应遗传算法支持向量机沉降预测的平均误差为1.9%，较BP神经网络算法计算平均误差(24.6%)提高了22.7%。