基于强度折减技术的加筋土二级边坡参数敏感性分析

李继兰, 陈耀章

(1.悉地(苏州)勘察设计顾问有限公司 湖南分公司, 湖南 长沙 410000；2. 湖南省交通科学研究院有限公司)

1 概述

岩土工程领域中，为了保证边坡的稳定性，通常会采取在土体中加入土工格栅的措施来提高边坡的稳定性。在土体中加入土工格栅可以提高边坡的整体性，控制边坡侧向位移，提高土体抗剪强度。近年来，国内外学者对加筋土边坡的稳定性进行了一系列卓有成效的研究。崔新壮等对边坡临界高度进行分析，考虑了均匀布筋、上疏下密布筋和上密下疏布筋模式，对工程应用给出了设计意见；王成皿等采用极限平衡法，对加筋土边坡的稳定性问题进行了研究；何叔航采用上限法，求解了破坏模式通过坡趾下方的二级加筋土边坡临界高度，结果可以指导边坡失稳分析；Michalowski假定加筋层不同破坏模式，分析不同破坏模式下加筋土对稳定性系数的影响。

上述研究采用的分析指标为稳定性系数或临界高度，未能与工程上通用的安全系数指标形成统一，带来诸多不便。石挺丰等对此进行了研究，通过极限分析获得了加筋土边坡的安全系数上限解，研究结果对工程有指导性作用；冯学茂等采用强度折减法研究了加筋格栅的参数对安全系数的影响。然而，在实际工程中，由于受到施工条件的限制，常出现二级或者多级的高边坡，而采用极限分析计算此类边坡稳定性安全系数的研究较少。因此，该文基于极限分析对加筋土二级台阶边坡稳定性进行研究。通过构建加筋土二级边坡破坏模型，推导出筋材所提供功率的表达式，并引入到临界状态的极限方程。借助强度折减技术，计算得到不同条件下的安全系数。通过现有研究成果验证该文提出方法的正确性，最后通过正交试验方法研究不同参数的敏感性。

2 破坏机构

加筋土加固边坡破坏机制通常为滑移类型的破坏。基于极限分析上限法，二级边坡的破坏模式如图1所示。假设滑动块ABCDEA为刚性，绕O点以角速度ω顺时针发生旋转破坏。r0和rh分别为初始旋转半径和终止旋转半径，其与水平面的夹角分别为θ0和θh；H为二级台阶边坡总高度；L为AB长度；d为台阶平台长度；β1和β2分别为上、下坡角，α1和α2分别为二级台阶边坡上下边坡相对应的高度系数，α1+α2=1。其中对数螺旋方程为：

r=r0exp[(θ-θ0)tanφ]

(1)

式中：φ为内摩擦角；θ为旋转半径r与水平面的夹角。

由几何关系可得：

(2)

(3)

图1 加筋土二级边坡破坏模式

对于筋材的设置，假设筋材仅受拉，不抗弯和抗压，该文对均匀布筋形式下的二级边坡进行研究，定义k0为平均布筋强度，即：

(4)

式中：T为纵向单位宽度筋材所能提供的抗拉拔强度；s为竖向的筋材间距。

3 外力功率及内能耗散

假设筋材的破坏方式为受拉破坏，因此，外力功率由重力提供，破坏机制的内能耗散由速度间断面上土体和筋材能量耗散构成。

由Chen提出的叠加法可求重力所做功率：

Wγ=WOAE-WOAB-WOBC-WOCD-WODE=ωγr03·(f1-f2-f3-f4-f5)

(5)

式中：WOAE、WOAB、WOBC、WOCD和WODE分别为块体OAE、OAB、OBC、OCD和ODE重力所做功率；γ为土体重度；其中，f1、f2、f3、f4、f5分别为块体OAE、OAB、OBC、OCD和ODE重力所做功率的几何形状系数，表达式如下：

f1={(3tanφcosθh+sinθh)exp[3(θh-θ0)tanφ]-3tanφcosθ0-sinθ0}/[3(1+9tan2φ)]

(6)

(7)

(8)

(9)

如图2所示，加筋土边坡发生破坏，其潜在滑裂面单位面积上筋材所消耗的功率为：

(10)

式中：η为筋材和边坡速度间断面之间的夹角，对于对数螺旋破坏机制，η=π/2+φ-θ；t为边坡滑动面的厚度；εx为筋材的拉伸应变率εx=Vsinηcos(η-φ)/t，

图2 筋材的拉伸破坏

因筋材不抗压，因此，当η-φ>π/2时，εx=0。

由式(10)可知：在边坡发生滑动使得筋材发生拉断破坏时，Er和边坡的潜在滑动面厚度t无关。

对式(10)进行积分，可得加筋土所提供的能量耗散功率：

(11)

f6的表达式如下：

(12)

图1所示破坏模式的内能耗散功率可表示为:

(13)

f7的表达式如下：

(14)

将内能耗散功率、筋材能量耗散及土体重力功率引入二级台阶边坡的能量平衡方程中，可得：

Wγ=Dr+Dint

(15)

4 安全系数的求解

在求解边坡安全系数时，通常要引入强度折减法。此方法是将边坡土体的黏聚力及内摩擦角以折减系数Fs进行折减，而边坡在折减后的土体强度参数cf和φf下，达到了稳定的临界状态。这个折减系数Fs称为边坡的安全系数：

(16)

借助强度折减法，通过对式(15)的求解，获得二级台阶边坡安全系数隐式解：

(17)

其中：

(18)

进行参数优化时，需在图1所示的边坡破坏机制的几何约束条件下进行，且满足：

(19)

5 结果分析

5.1 结果比较

为验证该文方法的有效性，将已有研究文献结果和该文结果进行对比，如表1所示。崔新壮等计算得到了不同参数条件下加筋土一级边坡的临界高度。在边坡高度等于临界高度的情况下，边坡处于临界破坏状态，即安全系数等于1.0。在β1=β2，且d=0的条件下，二级边坡退化为一级边坡。此时，对于加筋与非加筋情况，该文结果与文献[1]结果基本一致，两者的最大差距为1.4%，验证了该文加筋模式的有效性。此外，邓国瑞等对不考虑加固情况下的二级台阶边坡稳定性进行了研究。如表1所示，在不考虑加筋土加固作用时，该文所得安全系数与文献结果的差距分别为2.3%、2.2%和1.5%，计算结果基本一致。当考虑加筋作用时，安全系数分别上升了25.1%、30.2%和12.8%，可见土体中加入土工格栅可以有效提高边坡的稳定性。

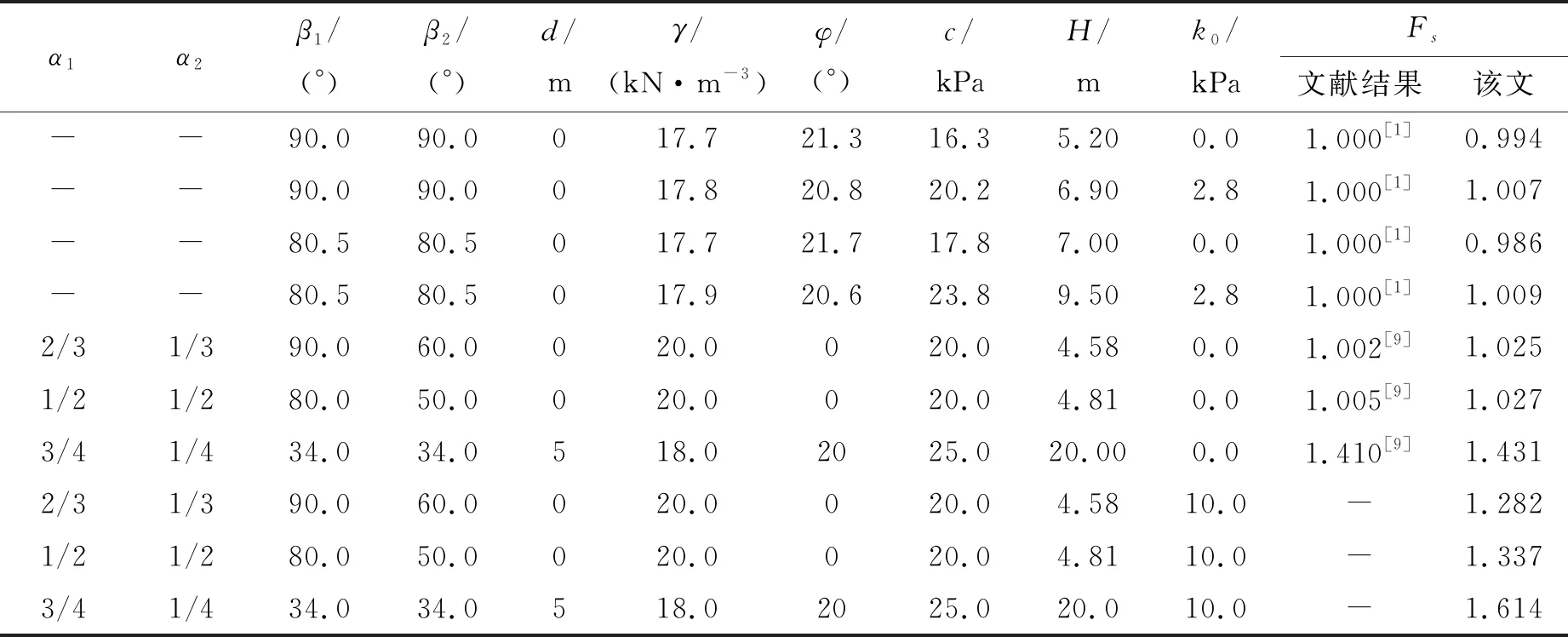
表1 加筋土边坡安全系数与文献[1]、[9]结果的比较

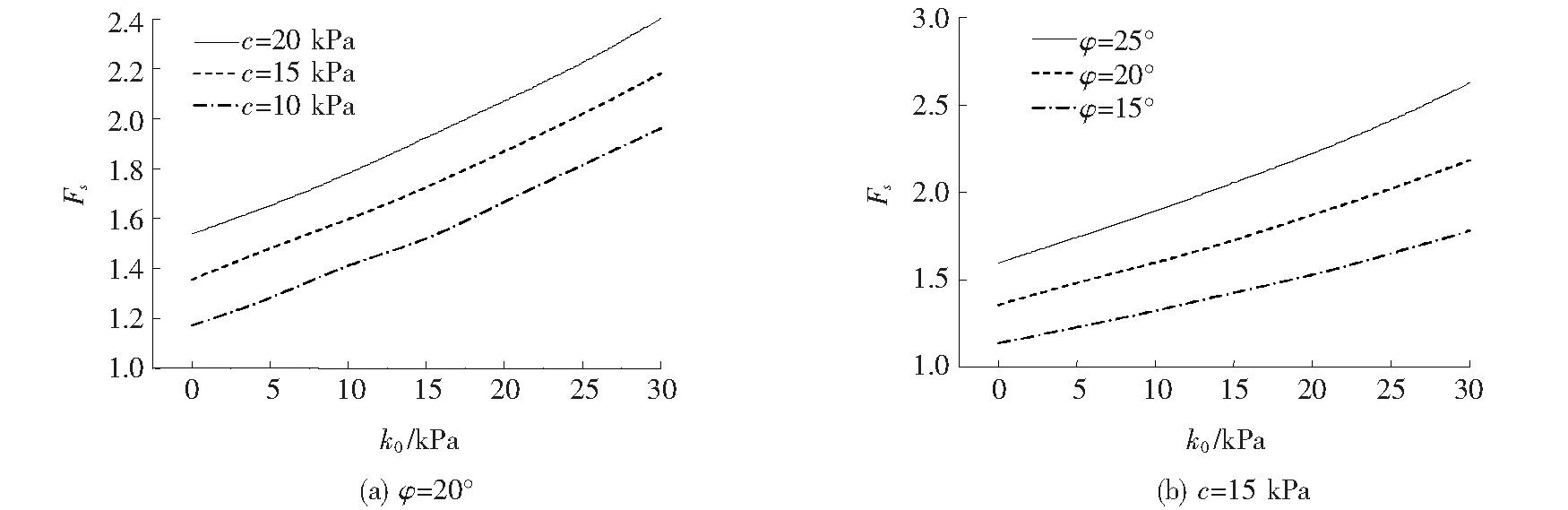
图3 平均布筋强度k0对Fs的影响

5.2 布筋强度对边坡稳定性的影响分析

图3(a)和3(b)为边坡安全系数在不同土体黏聚力和内摩擦角条件下随着平均布筋强度的增大而变化的规律。参数取值为：H=15 m，α1=0.5，β1=30°，β2=40°，d=3 m，k0=0～30 kPa。

由图3可知：平均布筋强度对土体边坡稳定性有显著影响，边坡稳定性安全系数随着平均布筋强度的增大近似线性增大。此外，在不同的黏聚力情况下，平均布筋强度对安全系数的影响规律曲线接近平行；而在不同内摩擦角情况下，当内摩擦角较小时，曲线较为平缓，当内摩擦角较大时，曲线增大幅度变大。

5.3 参数敏感性分析

选择7个参数：边坡总高度H、边坡高度系数α1、平均布筋强度k0、土体黏聚力c、内摩擦角φ及边坡上下坡角β1、β2。每个参数各水平都进行了6组试验，正交试验方案如表2所示。安全系数及极差分析结果如表3、4所示。计算时取土体重度γ=18 kN/m3、平台宽度d=2 m。比较各参数3个水平的平均值，即可得到该参数对边坡稳定性的影响规律。以平均布筋强度k0为例，其3个水平的安全系数平均值分别为：1.050、1.181、1.252，说明平均布筋强度k0越大，安全系数越大。表4各参数3水平变化规律表明：边坡安全系数随边坡高度、边坡上下坡角增大而减小，随平均布筋强度、边坡高度系数、黏聚力和内摩擦角增大而增大。由极差分析可知,各参数的敏感程度排序为：φ>c>β2>H>β1>k0>α1。土体内摩擦角对安全系数的敏感性最大，而边坡高度系数最小；土体黏聚力、边坡下坡角和边坡高度对安全系数敏感性较大，而平均布筋强度及边坡上坡角较小。

表2 正交试验方案

表3 正交试验表

续表3

试验号H/mα1k0/kPac/kPaφ/(°)β1/(°)β2/(°)Fs10120.420181540301.76611120.510122050401.06812120.615151030501.03113150.415181050400.90314150.520121530500.97615150.610152040301.45416180.420152030401.45717180.510181040500.81418180.615121550300.979

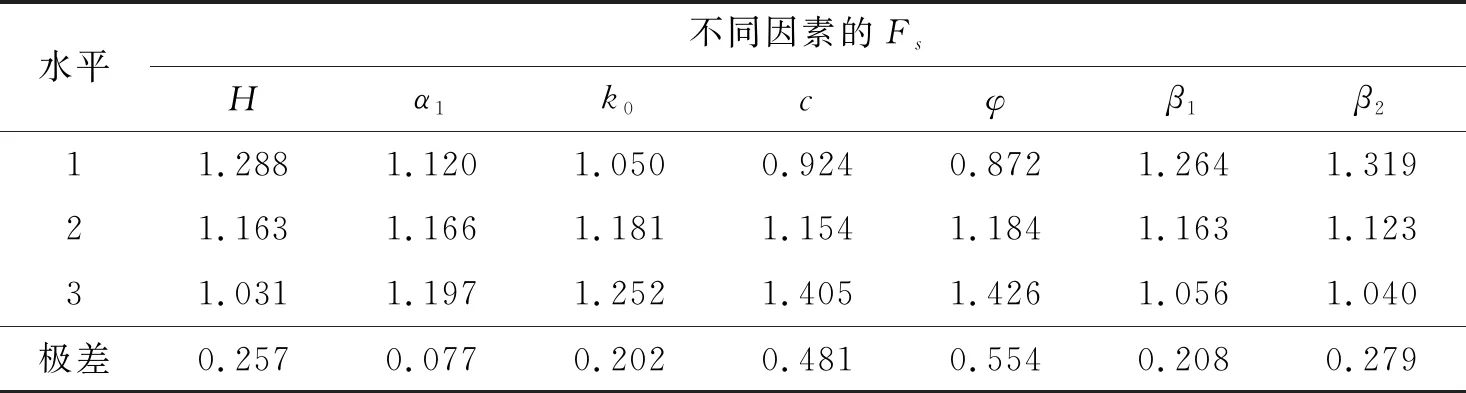
表4 正交试验Fs极差分析结果

6 结论

(1) 基于极限分析理论，构建加筋土二级台阶边坡破坏模型，推导了计算加筋土内能耗散的表达式，并导入功能平衡方程。借助强度折减技术，建立了计算安全系数的隐式表达式。借助最优化算法，求得安全系数。对比表明：该文的计算结果与已有文献结果较为接近，验证了该文方法的有效性。

(2) 通过对不同条件下的计算结果分析表明：二级边坡的安全系数随着平均布筋强度的增大近似线性增大。在不同的黏聚力情况下，平均布筋强度对安全系数的影响规律曲线接近平行；而在不同内摩擦角情况下，当内摩擦角较小时，曲线较为平缓，当内摩擦角较大时，安全系数增大幅度变大。在此基础上，采用正交试验方法研究了不同参数的敏感性：土体内摩擦角的敏感性最大，而边坡高度系数最小。此外，土体黏聚力、边坡下坡角和边坡高度的敏感性较大，而平均布筋强度及边坡上坡角较小。