某越野车悬架下摆臂的结构轻量化设计

严 君 杨世文 卢建志

中北大学 机电工程学院 030051

前言

现今社会，节能与环保成为汽车工业发展的主旨，汽车轻量化设计研究作为其中的重要课题越来越受到各方面的关注。传统的汽车零部件的结构材料以钢板为主，已经无法适应人们对汽车高速与轻量化的追求。目前国内外汽车结构轻量化的研究方向主要集中在两个方面：一是开发具有比模量和比强度高的轻质高性能材料来替换原来的钢板材料；二是采用结构优化技术设计出轻量化结构来取代原有结构[1]。

国内外有关悬架摆臂的结构优化设计研究有桑楠，白玉等主要是利用ABAQUS软件对某汽车的前摆臂进行了有限分析，在此基础上为了进一步改善结构的承载能力和降低结构的质量，提出了该摆臂结构轻量化设计的方案[2]；王凤军，扶原放等提出了基于可靠性理论，以提高结构的可靠性作为结构优化设计的目标，结合有限元结构优化方法进行某悬架下摆臂的轻量化设计研究[3]；张兆良则利用Hypermesh软件进行了某双横臂悬架上下摆臂的拓扑优化分析和刚、强度分析，同时设计了上下摆臂的轻量化结构[4]；祝小元，方宗德等提出了多工况下针对汽车悬架控制臂结构进行了以静态柔度和低阶振动固有频率的多目标拓扑结构优化研究，解决了静态的摆臂刚度问题和动态的摆臂低阶振动频率问题[5]；上官文斌,蒋翠翠等研究了含有球铰和衬套的汽车悬架控制臂优化设计模型，利用拓扑优化技术对悬架控制臂进行了优，根据优化结果重新设计了悬架的控制臂并对其进行了应力、刚度和固有频率的计算[6]；Dong-Chan Lee 和 Jeong-Ick Lee[7]对铝合金摆臂进行了拓扑优化和有限元分析，提出了新型铝合金摆臂的轻量化设计结构，并实现了制造和应用；B-C Song，Y-C Park[8]等人对某车的悬架上摆臂利用结构优化技术和Kriging插值优化理论进行了摆臂结构的轻量化设计。

1 基于密度法的拓扑优化理论

1.1 密度法拓扑优化设计变量

拓扑优化是结构优化方法中的一种，本文采用基于连续体的变密度法拓扑优化理论，建立单元密度和材料属性之间的关系。

基于变密度法思想，材料的刚度属性被假定的认为与密度成线性关系，其方程表达式如下所示。每个单元的杨氏模量Ei可以用方程式（2）来表示。

式中，ρi是第i个单元的材料密度；ρ0初始的材料密度；xi为相对密度；Ei为第i个单元杨氏模量；E0为原始的杨氏模量；n为惩罚因子。其中相对密度xi就是拓扑优化密度法的设计变量。

1.2 设计变量与材料属性的关系

相对密度是拓扑优化密度法的设计变量，它由空间的微结构（单胞）确定，单胞结构的增删决定了相对密度值的大小，即在密度区间[0，1]之间存在着中间密度单元。每个微结构的设计变量则是空间矩形的宽度、深度以及方向，由此来定义材料的密度和弹性[9]。平面单元和实体单元相对密度与空间尺寸的关系和表示方法如图1所示。

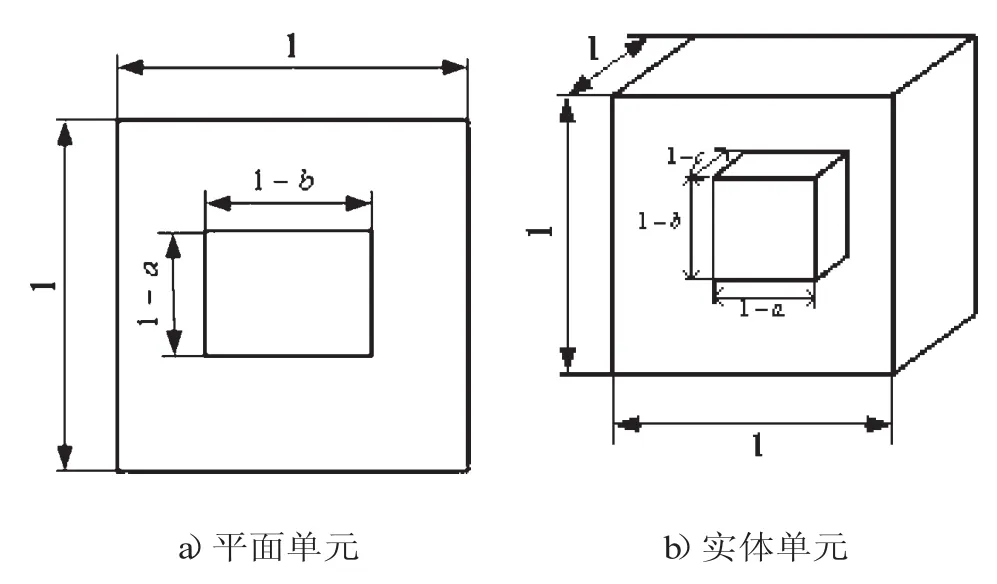
图1 相对密度微结构单元

平面单元的相对密度为：

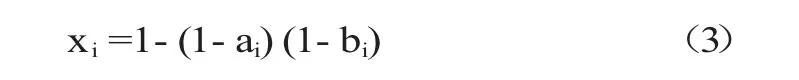
式中(1-a)(1-b)代表的是一个单元所占的空间面积。当a=b=0，表示单元为空，即xi=0；当a=1或b=1时，则表示该单元为实，即相对密度xi=1。

实体单元的相对密度为：

由应力—应变关系，{б}=[D]{ε}，式中弹性系数与相对密度的关系如方程（5）～（7）所示。

各向同性材料的平面应力应变的弹性系数[D]与相对密度的关系矩阵为：

将式（3）代入式（5）中可得弹性系数矩阵与空间单元尺寸参数之间关系为：

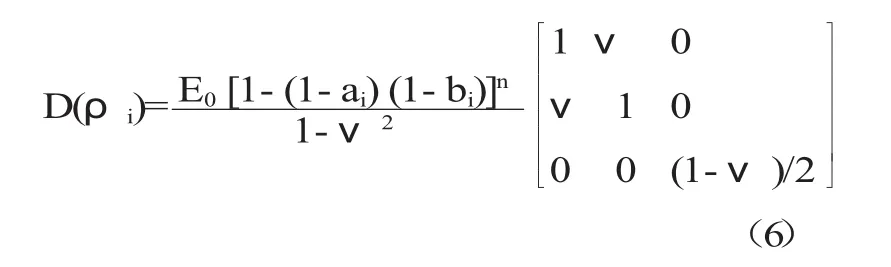
同理，各向同性材料的实体单元的弹性系数[D]与结构设计变量相对密度之间的关系矩阵为：

1.3 设计变量与结构的单元刚度关系

在有限元静力学求解时，当结构的变形在材料弹性范围以内时，结构刚度和位移之间的关系则满足广义的胡克定律，其方程为：

因此结构的单元刚度矩阵[K]与设计变量之间的关系可以表示为：

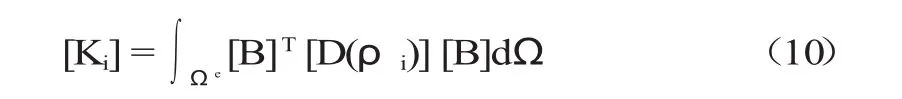
式中：[B]矩阵为常系数矩阵。

2 悬架摆臂的工况分析

汽车悬架摆臂相对于整个车体结构的布置和设计来说是很小的一个部分，但是它却传递着来自路面的一切力和力矩，因此汽车悬架摆臂的工况分析是设计摆臂结构的一个重要环节。

汽车悬架下摆臂最典型的三种极限工况为：

（1）垂直冲击工况；路面对车轮的垂直冲击力通过转向节、球头销、摆臂和螺旋弹簧传到车架和车身上，此时车轮所受的垂直力最大，纵向力和侧向力相对较小，其影响忽略，在整车坐标系下车轮的纵向力FX=0，侧向力 FY=0。

（2）转弯工况；作用在车轮上的侧向力矩及其力矩由转向节及其导向机构经过悬架传递到车架上，考虑急转弯的极限情况，此时纵向力相对于侧向力较小，可以忽略，因此有车轮的纵向力FX=0。

（3）制动工况；制动工况时，轮胎的纵向力达到最大，此时侧向力较小可以忽略，则有FY=0。

根据某越野车悬架下摆臂的结构尺寸和在整车中的布置位置关系，这三种工况下该越野车悬架下摆臂的载荷大小如表1所示，表1中的数据是已经换算到了摆臂坐标系下的载荷关系。

表1 三种工况的载荷情况

3 多工况悬架摆臂拓扑优化数学模型

3.1 多工况结构优化的定义

本文设计的越野车悬架下横臂主要应用的工况有极限垂直冲击、转弯、刹车三种，在对锻铝合金材料对下横臂进行概念设计阶段的拓扑优化时，如果采用单工况拓扑优化方法，所使用的工程分析时间比较长，有可能需要几轮的优化和几何重构过程。这不仅仅加大了设计的时间成本，而且所设计出的结构不一定是最优的、满足各工况性能要求的结构。基于此本文提出了基于加权应变能的拓扑优化方法来处理在拓扑优化阶段的多工况问题。

在Optistruct结构优化设计中，加权应变能响应的定义为每个子工况应变能的加权和，其表达式为：

式中，Cj为第j个工况的应变能；ωj为该工况的加权系数，其取值范围在0.1～1.0之间；uTi为位移矩阵的转置。

通过加权应变能的加权和定义了每个子工况在摆臂结构拓扑优化下的权重，该权重根据摆臂在汽车悬架工作中的真实情况来评定，这样结构优化设计的结果将会更加的接近实际情况。

3.2 拓扑优化数学模型

基于加权应变能的拓扑优化方法，该方法以极限垂直冲击、转弯、刹车三种工况的加权应变能最小为目标函数，以设计区域的体积分数为约束，以设计区域的材料密度为设计变量。

在结构的拓扑优化过程中，把刚度最大问题等效为柔度最小问题来研究，柔度则用应变能来定义。因此，该问题的优化目标可以转化为全局柔度最小问题。采用Optistruct模型常用的多刚度线性叠加的模型将多个工况下的柔度目标值综合表述为全局柔度目标值，因此拓扑优化的数学模型为：

式中，Ω为拓扑设计区域；V0为结构初始体积。

因此，某越野车锻铝合金下摆臂多工况下的拓扑优化问题的描述如下：

优化区域：如图2所指示的区域；

目标函数：悬架下横臂的整体刚度最大，即加权应变能最小；

约束条件：悬架下横臂的体积分数大于0.4小于0.6；

设计变量：单元的密度值；

制造工艺约束：脱模约束；

最大应力参数约束：小于355MPa。

图2 摆臂结构拓扑几何模型

4 结果和分析

4.1 摆臂结构的拓扑优化结果

结构拓扑优化设计采用商用软件Hyperworks中的Optistruct优化设计模块完成。经过18次迭代，结构优化计算收敛，将计算结构文件导进hyperview软件后，查看优化后的模型。图3是优化计算的迭代过程图，图4是单元去年密度值大于0.3的密度云图。

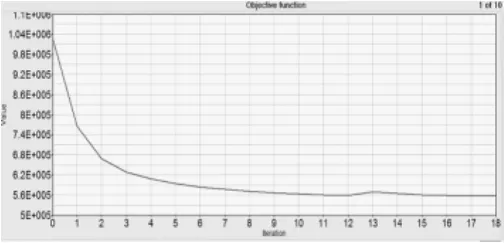
图3 拓扑迭代图

图4 摆臂密度云图

根据结构拓扑后的密度云图，取材料密度值大于0.3的部分对悬架下摆臂的结构进行三维建模并获得了锻铝合金下摆臂结构，悬架下摆臂的CAD模型图如图5所示。

图5 锻铝合金下摆臂结构

4.2 摆臂结构有限元分析结果

为了将拓扑优化后的铝合金摆臂结构与铸钢材料的结构性能进行对比，本文采用有限元分析方法分别对两种材料的结构进行了三种工况下强度和刚度分析。有限元分析的结果如表所示。

（1）铸钢材料下摆臂的有限元分析结果

三种工况下最大应力和最大位移值如表2所示。

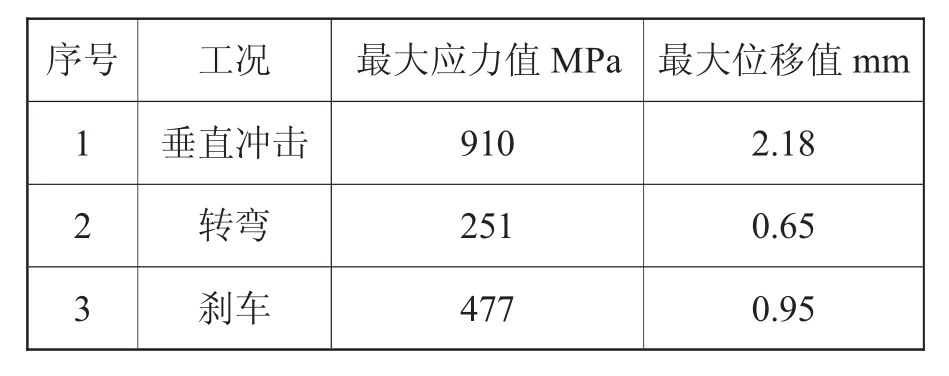
表2 锻钢下摆臂有限元分析结果

（2）铝合金材料下摆臂的有限元分析结果

铝合金拓扑优化下摆臂结构在三种工况下的最大应力和位移值如表3所示。

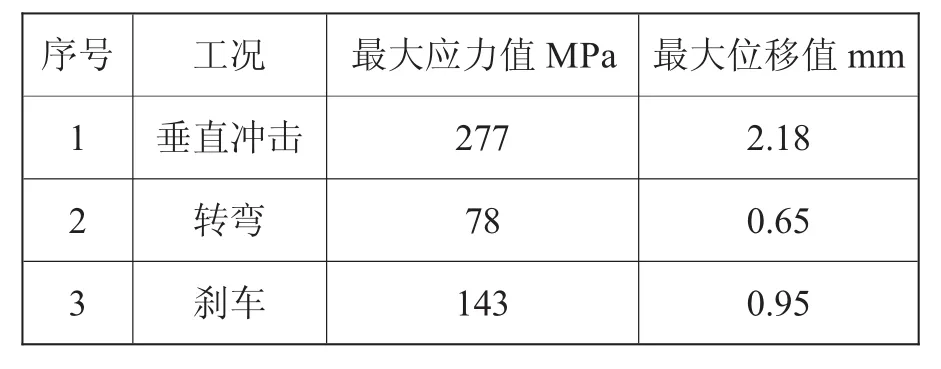
表3 铝合金下摆臂有限元分析结果

（3）结果分析

根据有限元分析的结果，为了验证和评价拓扑结构的性能，将对铸钢摆臂和铝合金摆臂从强度、刚度和结构重量三个方面进行对比分析。摆臂结构性能对比如表5所示。

表4 铸钢材料与锻铝材料下横臂性能对比

1）强度分析

由表5可知，两种不同材料的强度对比：铝合金材料下横臂的最大应力为277 MPa，铸钢材料下横臂的最大应力为910 MPa，都小于各自材料的屈服极限，满足项目中所提出的设计要求。

2）刚度分析

由以上两种材料下横臂的刚度分析可知：铝合金的下横臂在垂直冲击工况的最大位移比铸钢材料的小了0.17mm，转弯工况小了0.26mm，刹车工况小了0.34mm，锻铝材料下横臂结构刚度比锻钢材料结构在三种工况下都有提高和改进。

3）结构重量对比

由表5对两种不同材料的下横臂的质量对比可知，锻铝材料下横臂的重量为11.04 Kg，比铸钢材料的下横臂减小了1.52 Kg，由于该越野车前后悬架都采用双横臂式独立悬架，这样，该越野车如果采用铝合金材料制造下横臂的话，那么在下横臂上可以减重1.52X4=6.08Kg，相对于铸钢材料下横臂，铝合金材料减重约12.10%。

5 结论

通过有限元分析以及与铸钢材料摆臂结构性能对比可以证明，拓扑优化可以减轻摆臂质量，同时改善摆臂的刚、强度特性，对于汽车轻量化设计有着重大意义。

[1]谢文林.车用塑性零部件生产情况及2000年市场需求预测[J].汽车世界,1997,(2)：29～31.

[2]桑楠,白玉等.基于ABAQUS的汽车前摆臂轻量化设计[J].长春工程学院学报,2010,(11)2.

[3]王凤军,扶原放等.基于可靠性原理的悬架下摆臂轻量化设计研究[J].汽车工程,2009,(31)11.

[4]张兆良.双横臂悬架上、下摆臂轻量化设计[J].北京汽车,2010,2.

[5]祝小元,方宗德等.汽车悬架控制臂的多目标拓扑优化[J].汽车工程,2011,(33)2.

[6]上官文斌,蒋翠翠等.汽车悬架控制臂的拓扑优化与性能计算[J].汽车工程,2008,(30)8.

[7]Dong-Chan Lee,Jeong-Ick Lee.Structural optimization concept for the design of an aluminum control arm[J].Automobile Engineering,2003,Vol.217.

[8]B-C Song,Y-C Park,S-W Kang,K-H Lee.Structural optimization of an upper control arm,considering the strength[J].Automobile Engineering,2009,Vol.223.

[9]张胜兰等.基于Hyperworks的结构优化设计技术[M].机械工业出版社,2007.