铁路危险货物运输安全的模糊综合评价

2011-09-03 13:12李颖

铁道货运 2011年10期

李颖

（西安铁路职业技术学院交通运输系，陕西西安 710014）

随着我国石油、化工等行业的发展，铁路危险货物的运量不断增长。但是由于危险货物运输业务涉及全路 18 个铁路局及公司，且各单位运输危险货物的品种、运量、办理站及专用线数量等均不相同，因此，在危险货物运输安全状况上存在一定差异和风险。危险货物运输事故一旦发生，就会对铁路周围的生态环境造成严重污染和破坏，因此，评价铁路危险货物运输安全是预防危险货物运输事故发生的前提。针对层次分析法和模糊综合评价法存在的问题，以下将采用改进的层次分析法计算各个指标的权重，并利用模糊综合评价法进行评价；在模糊综合评价中，采用了三角打分法和圆形分布隶属函数。

1 基于改进的层次分析法的多级模糊综合评价方法原理

传统的层次分析法由于使用 1～9 标度具有不足之处。例如：当指标1稍优于指标2时，按 1～9 标度，其权重比为 3∶1，即前者的重要程度是后者的3倍。这与评判者“稍优”的实际想法不尽相符。因此，本文采用 9/9～9/1 标度对权重进行计算，两者之间的重要程度是由通式 9/(10－K)，其中K表示比较级别分别取1至 9，得到2种标度值对比如表1所示。可以看出新标度当指标1稍优于指标2时，其权重比为 1.286∶1。这与评判者“稍优”的实际想法较接近，因而精度较好[1]。

表 1 2 种标度及其各自的含义

基于改进的层次分析法的多级模糊综合评判法步骤[2]如下：

（1）建立综合评价因素集。设U={u1，u2，…，um}为影响被评价对象的m种因素。

（2）确定各指标的权重向量A。① 计算判断矩阵每一行元素的乘积Mi；② 计算Mi的n次方根：=；③ 将向量，…，}T归一化即为所求的特征向量；④ 计算判断矩阵的最大特征根λmax；⑤一致性检验。

（3）确定评语集V={v1，v2，…，vn}，n为评语个数。在此，令安全等级评语集={好，较好，一般，较差，差}，其对应的取值论域Ω={5～4，4～3，3～2，2～1，1～0}。

（4）建立隶属度函数。即对指标集内诸因素的评价建立一种模糊映射f：U→V。对于数量型指标可以根据评价指标和评价标准的要求建立隶属度函数。

（5）建立模糊关系矩阵R。R是单指标评价的结果，即单指标评价矩阵。模糊综合评价所评价的对象正是R。

（6）求评价结果向量B。B=AT×R。它是对每个被评价对象综合状况分等级的程度描述。

2 实例分析

2.1 建立铁路危险货物安全评价指标体系

以某企业为例，在分析铁路危险货物运输特点及其影响因素的基础上，依据国家安全生产的相关法规和铁路危险货物运输现状，并结合了 10 位专家学者的调查意见，针对以往铁路危险货物运输安全评价指标的不足，构建了关于铁路危险货物运输安全的评价指标体系，如表2所示。

表 2 铁路危险货物运输安全评价指标体系

2.2 用改进的层次分析法确定指标权重

2.2.1 构造判断矩阵

传统的调查是直接让专家在矩阵中填写各指标两两比较的标度，但当指标比较多时容易造成混乱和错误。而且不同专家由于其专业背景、工作经验、个人性格的不同对于“稍微重要、明显重要、强烈重要、极端重要”的认识和把握会有所差别且不稳定。本文在调查中不再让专家填写各指标两两比较的标度，而是填写各指标对上级指标的影响，其中影响程度分五级 (很大、大、一般、小、很小)，请专家根据自己的意见在相应的栏内直接打“ ”。以专家1对危险货物运输安全这个一级指标调查为例，调查结果如表 3所示。

将专家1对于各二级指标对应一级指标相对重要度的调查结果两两比较，结合查找表 4 中 9/9～9/1标度对应值，最终得到判断矩阵。例如：专家1认为在影响危险货物运输安全的一级指标中从业人员素质u1的影响大，运输安全管理制度u2的影响一般，则查表4可知u1与u2比较值的对应值为 1.286。同理可得到其他指标两两对比的结果。判断矩阵具有以下性质：cij＞0；cii=1；cij=1/cji。

2.2.2 根据判断矩阵使用方根法计算权重

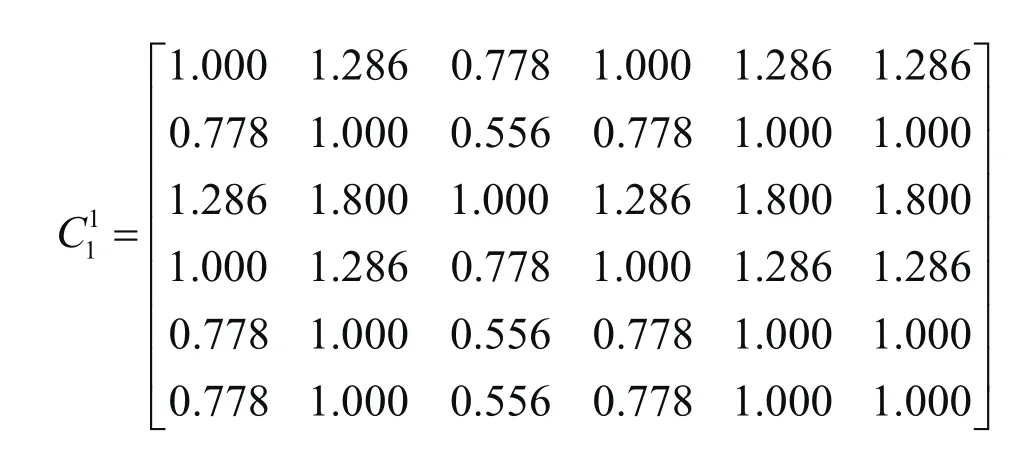
（1）计算判断矩阵每一行元素的乘积Mi得：

（2）计算Mi的n次方根，此处n取 6，得：

即为所求的特征向量，也就是权重向量。

（4）计算判断矩阵的最大特征根λmax：

表 3 一级指标权重原始调查表(专家1)

表 4 专家调查结果与9/9～9/1标度对应值

（5）进行指标一致性检验：

CI=(λmax－n)/(n－1)=(6.002－6)/(6－1)=0.000 5，查得n=6 时，RI=1.24，得到：

CR=CI/RI=0.000 5/1.24=0.000 4＜0.1

则专家1给出的准则层指标的权重集A11=(0.177，0.136，0.238，0.177，0.136，0.136)T。

其他9位专家的计算过程和专家1完全一致，不再复述。将 10 位专家给出的权重汇总求平均得出一级指标最终权重集为：A=(0.188，0.196，0.206，0.150，0.142，0.118 )T。

同理，求得二级指标的权重为：A1=(0.273，0.349，0.378)T；A2=(0.220，0.194，0.179，0.184，0.214)T；A3=(0.260，0.231，0.249，0.260)T；A4=(0.249，0.185，0.146，0.203，0.217)T；A5=(0.351，0.330，0.319)T；A6=(0.314，0.306，0.380)T。

2.3 建立评价集确定指标的隶属度

2.3.1 现场三角模糊打分情况

对一个指标进行单隶属度评判时，可采用三角模糊数打分法。首先，对指标打出最有可能值m，表示对此指标相互关系的基本评价，接着标出上下界a和b。下界表示专家认为可能的最低评分，上界表示专家认为可能的最高评分，则该指标的最终得分为：x=(a+4m+b)/6[3]。

以u11为例，满分5分，由专家对其打分情况：最大值a=4，最小值b=3，最可能值m=3.25，故最终得分：x=(a+4m+b)/6=3.208。

2.3.2 用圆形分布隶属函数计算指标隶属度

根据构造隶属函数的基本原则，在任何模糊等级范围的中间区域虽然应保持一定的隶属度的稳定性，但也要体现该区域内的细微差别，即均可认为中点处可以定义为绝对属于该等级，即隶属度定为 1，随着与该中点的距离变大，属于该等级的隶属度就变小，而且其变化率应该是由小变大 (变化率最小值为 0)，当到达两连续等级中间点时，这种变化率应该是最大的，且此时两个隶属度相等，都为 0.5，过了该中间点变化率则又是由大变小，直到为 0。本文构造了圆形隶属函数，函数形式如下：

（1）偏小型：

式中：b=a+1。

（2）偏大型：

式中：b=a+1。

（3）中间型：

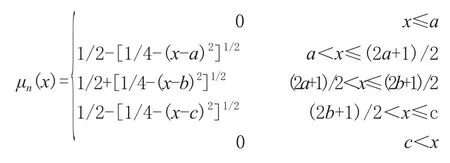
式中：b=a+1；c=b+1。

每个评语等级都有对应的隶属函数。因为满分是5 分，因此，得分在 0～1 之间是“差”，1～2 之间是“较差”，2～3 之间是“一般”，3～4 之间是“较好”，4～5之间是“好”。考虑了模糊理论以后，任一分值可能对相邻的两个等级都有隶属度，比如 2.8对“一般”有一定的隶属度，同时对“较好”也有一定的隶属度，所以“较好”、“一般”、“较差”这3个等级的隶属度函数是中间型的。

对于 0～1 之间的分值情况有所不同，0.5～1 之间的分值对“差”和“较差”都有一定的隶属度，而0～0.5之间的分值绝对属于“差”，对“差”的隶属度为 1，对“较差”的隶属度为 0，故0～1之间的隶属度函数为偏小型。

4～5 之间隶属度函数情况类似，4～4.5 之间的函数对“好”和“较好”都有一定的隶属度，但 4.5～5之间的数值肯定是“好”这一等级的，对“好”的隶属度为 1，对“较好”的隶属度为 0。所以其函数是偏大型的。

因此，“差”这一等级的隶属函数是偏小型的，“好”这一等级的隶属函数是偏大型的。将 3.208代入5个等级的隶属函数，可知其对“好”、“较差”、“差”这3个等级的隶属度为 0，对“较好”这一等级的隶属度为 0.906，对“一般”这一等级的隶属度为 0.094，所以 3.208 对各等级的隶属度向量为：r11={0.000，0.906，0.094，0.000，0.000}。其他指标的单隶属度的确定同上，其结果如表5所示。