一种基于ESO的导弹鲁棒自动驾驶仪设计方法①

董飞垚，雷虎民，邵 雷，张金鹏

(1.空军工程大学导弹学院，三原 713800;2.中国空空导弹研究院，洛阳 471009)

0 引言

针对飞行器控制过程中存在的干扰和未建模特性，近年来，国内外学者展开了广泛研究［1－7］。文献［1］基于增益调度思想设计了飞机的一种自动驾驶仪，但针对高速飞行器，采用该方法系统的快速性和鲁棒性变得较差;文献［2］依据H∞控制理论设计的导弹鲁棒自动驾驶仪具有很好的鲁棒稳定性能，但是其控制器形式过于复杂，限制了其实际工程应用;文献［3］采用最优控制来保证系统的快速性和鲁棒性，但是反馈所需的状态量在实际工程中并不都能获得;文献［4］通过设计一种基于滑模理论的干扰观测器来增强系统的鲁棒性，但其控制律设计中需要已知系统不确定性的上界，保守性很大，且容易引起控制量的饱和问题。扩张状态观测器(ESO)是将系统中含有的非线性动态、模型不确定性及外界扰动等都视为扩张状态加以观测，其本身并不依赖于生成扰动的具体模型，也不需要直接去测量其作用，是通用的扰动观测器［8］。

本文提出了一种基于扩张状态观测器的导弹滚转自动驾驶仪设计方法，保证导弹在大机动和强干扰下具有较好的动态性能和强鲁棒性。

1 非线性扩张状态观测器

考虑如下一类n阶SISO非线性系统:

式中 x=［x1x2… xn］T表示系统的状态;ƒ(x)和g(x)为已知标量函数;Δƒ(x)、Δg(x)和w表示未知不确定性和外界扰动;u为控制输入;y为系统输出。

定义d=Δƒ(x)+Δg(x)+w为作用于系统的复合干扰，并将其作为系统(1)的一个扩张状态xn+1，则系统(1)可扩展为n+1阶系统:

针对上述系统，采用如下非线性观测器(NESO):

可见，只要βi和gi选择恰当，状态估计值就能精确逼近实际值xi，即→xi。所以gi的选择极其关键，目前大多采用如下带有线性区的非光滑函数［9］:

其中，0 ＜μi＜1，i=1，2，…，n+1，δ＞0 为 gi切换的阈值。可以看出，函数 gi的一个重要特性是当误差较小时，gi有较大值，相反当误差较大时，gi具有较小值。

2 模型描述

导弹滚转通道控制系统由速率陀螺、舵机和控制算法等组成。其中速率陀螺用来测量导弹的滚转角速率，进而通过积分获得滚转角，舵机用来响应由控制算法生成的副翼偏角指令，形成副翼偏角，产生相应滚转力矩，抑制和消除弹体滚转。

舵机一般可用二阶模型来描述:

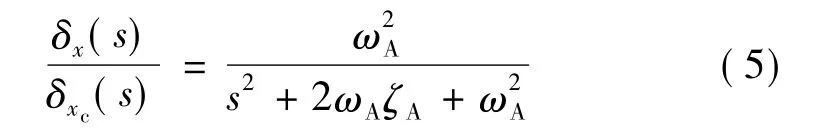
式中 δx和δxc分别为副翼偏角和副翼偏角指令;ωA和ζA分别为舵机的自然频率和阻尼。

根据文献［10］，不考虑俯仰、偏航和滚转通道耦合情况，导弹滚转通道的刚体数学模型可写成:

式中 γ为导弹输出滚转角;Kδ为导弹副翼效率系数;Kdx和Tdx分别为导弹滚转传递系数和滚转时间常数。

联立式(5)和式(6)，可得从副翼偏角指令δxc到导弹滚转角γ的传递函数:

式中 b=KδKdxω/Tdx，a0=0，a1= ω/Tdx，a2=(Tdxω+2ωAζA)/Tdx;a3=(1+2ωAζATdx)/Tdx。

考虑到空气动力系数的不确定性，ai(i=1，2，3，4)和b并不能精确获得，所以 ai=ai0+Δa，b=b0+Δb，其中ai0和b0表示所对应系数的标称值，Δa和Δb表示相应的不确定性。此外，为了后续仿真验证，给出弹性弹体和速率陀螺的模型，分别为G1(s)和G2(s):

以上模型参数的取值如表1所示，表中det为等效外界扰动。

表1 各模型参数数值表Table 1 Value of parameters in each model

3 控制算法设计及稳定性分析

为便于分析和设计，将式(7)写成如下形式:

式中 x=［x1x2x3x4］T表示系统状态;uc=δx为控制输入;yp=γ为系统输出;Bd为干扰输入匹配矩阵;ds=φ－Δa1x1－Δa2x2－Δa3x3－Δa4x4+Δbu，表示作用于系统的复合干扰，φ为外界扰动;Ap、Bp和Cp分别为系统矩阵、输入矩阵和输出矩阵。

Ap、Bp、Bd和 Cp表达式如下:

同式(2)，若将ds作为系统的一个扩张状态x5，则式(10)可扩展为

其中: xpk= ［x1x2x3x4x5］T

容易判断(Ap，Bp，Cp)可控可观测，根据文献［11］，若被控系统可控可观测，用状态观测器估计值形成状态反馈时，其系统的状态反馈设计和观测器设计可分别独立进行。所以可先进行系统的控制算法设计。

3.1 控制算法

本文基于ESO所设计的控制算法包含两部分，分别是针对标称系统的最优控制项uc1和针对系统复合干扰的补偿项uc2。

针对标称系统，采用线性二次型调节器(LQR)进行控制，设计控制信号uc1，使得目标函数J取得最小值，J通常取如下形式:

式中 Q和R为所选择的加权矩阵和加权系数。

Q阵所有元素均非负，R为大于0的实数，分别取Q 和 R 为［12］

通过求解代数Riccati方程:

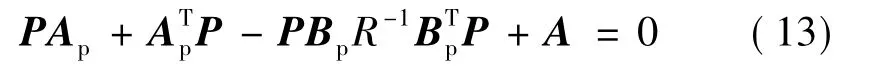
便可得J取得最小值的解:

控制信号中干扰补偿项uc2取

将uc=uc1+uc2代入式(10)可得

所以uc能保证系统(10)对外界扰动和自身未建模动态具有强鲁棒性。

依据文献［13］，当系统存在未知干扰和未建模动态时，利用观测状态设计的控制系统，其性能要优于直接利用系统实际状态所设计的控制系统。而且在导弹的实际飞行过程中，xp和ds并不能直接获取。为此引入ESO完成对系统状态的估计并将估计状态值用于状态反馈。

结合式(3)和式(11)，取 gi(eo1)=eo1，得

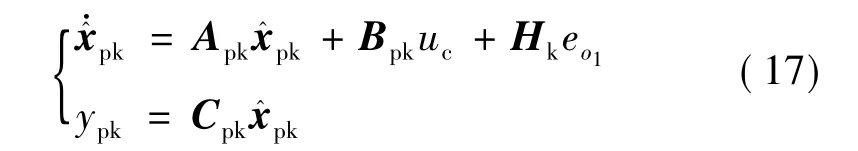
式中 Hk=［β1β2β3β4β5］为待确定的观测增益向量，通过式(17)可完成对系统状态的估计。

3.2 稳定性分析

如上节所述，因弹性或外界扰动带来的偏差，可在控制信号中加以补偿。根据式(17)所估计状态，控制算法为

将式(17)代入式(8)得

联立式(18)和式(19)得

由式(20)可看出，其系统矩阵为三角块矩阵，故其特征值仅由主对角线上各矩阵块的特征值决定，即由Ap－BpK和Apk－HkCpk的特征值决定。

根据上节的分析，Ap－BpK的特征值均具有负实部，所以若Apk－HkCpk的特征值具有负实部，则系统(20)渐近稳定。

由以上分析可知，保证系统稳定的前提是矩阵Apk－HkCpk的特征值具有负实部，而矩阵Apk－HkCpk的特征值可任意配置的前提是(Apk，Cpk)可观测。

下面证明(Apk，Cpk)亦可观测。

证明:定义 ei，i=1，2，…，5 为第 i行元素为 1，其他行元素均为0的列向量，则Apk和Cpk可分别表示为

式中 z1和z2分别为的第4列和第5列。

可观测性判定矩阵V如下所示:

不难发现，rank(V)=5，故(Apk，Cpk)可观测。

由于(Apk，Cpk)可观测，故矩阵 Apk－HkCpk特征值可任意配置。Hk阵参数的选取应遵循观测器响应速度比状态反馈系统的响应速度快的原则［8］。不难求解，依据控制算法式(14)，标称系统的极点被配置在－30，－202，－104.24±j182.91。由于其主导极点为－30，所以将矩阵Apk－HkCpk特征值配置在－45，便可得到观测矩阵Hk。

4 仿真结果及分析

为了便于验证本文所设计的控制算法的优越性，分别在以下3种情形下进行仿真:情形一为标称状态;情形二为仅考虑弹性干扰;情形三为同时考虑弹性干扰、外界扰动和陀螺的动态特性。仿真中模型参数取表1中的数值，系统初始状态设为:xp0=［5° 0 0 0］，仿真结果见图1～图4。

针对标称系统，利用系统的实际状态进行反馈，采用LQR控制，系统具有良好的动态性能，消除5°初始滚转角所需调节时间不大于0.15 s，且副翼偏角小于其最大容许值，如图1(a)所示;但考虑弹性干扰时，若仍采用LQR控制，系统将不稳定，如图1(b)所示。

基于Luenberger全维状态观测器(LO)对系统状态估计，并将估计值用于LQR控制中，当仅考虑弹性干扰时，系统渐近稳定，如图2(a)所示;但若同时考虑弹性干扰和外界扰动的情况下，基于LO状态观测器的LQR控制不但不能消除初始滚转角，反而使其增大到超过10°，如图2(b)所示。

图1 采用LQR时γ和δx变化曲线Fig.1 Curves of γ and δxwith LQR

图2 采用LQR+LO时γ和δx变化曲线Fig.2 Curves of γ and δxwith LQR+LO

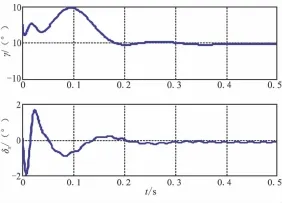
图3 情形三下采用LQR+ESO时γ和δx变化曲线Fig.3 Curves of γ and δxwith LQR+ESO in No.3 condition

图4 情形三下ESO系统状态估计值与实际值比较图Fig.4 Comparison between estimated value with ESO and actual value in No.3 condition

图3和图4为同时考虑弹性干扰、外界扰动和陀螺的动态特性情况下的部分输出曲线，可看出，ESO状态观测器能准确估计系统的实际状态和复合干扰，基于ESO估计状态的控制算法能消除弹性和外界扰动等因素带来的影响，保证滚转角在最短时间内收敛于零，且副翼偏角在其最大容许值以下。此外，在情形三下，取表1中模型参数40%的摄动值，基于ESO估计状态的所设计的LQR控制算法同样具有较好的控制效果，但由于篇幅所限，这里未能给出相应曲线。

5 结论

本文设计了一种基于ESO的导弹滚转鲁棒自动驾驶仪设计方法。仿真结果表明，在同时考虑弹性干扰、外界扰动和陀螺动态特性的情况下，所设计ESO状态观测器能准确估计系统的状态及干扰，控制算法能消除复合干扰带来的影响，具有良好的动态特性和强鲁棒性，从而克服了传统设计方法的缺陷，能保证导弹在高机动和强干扰下滚转通道的快速稳定。

［1］Lee C H，Shin M H，Chung M J.A design of gain-scheduled control for a linear parameter varing system:an application to flight control［J］.Control Engineering Practice，2001，32(9):11-12.

［2］Tan F，Duan G R，Zhao L J.Robust controller design for autopilot of a BTT missile［C］//Proc.of the 6th World Congress on Intelligent Control and Automation.2006(21-23):6358-6362.

［3］Kumaresan N，Balasubramaniam P.Optimal control for stochastic linear quadratic singular system using neural networks［J］.Journal of Process Control，2009，19(7):482-488.

［4］Hall C E，Shtessel Y B.Sliding mode disturbance observerbased control for a reusable launch vehicle［C］//AIAA Guidance Navigation and Control Conference and Exhibit.Reston:AIAA，2005:1-26.

［5］White B A，Bruyere L，Tsourdos A.Missile autopilot design using quasi-Lpv polynomial eigenstructure assignment［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(4):1472-1483.

［6］Batool Labibi，Horacio J M，Chen T W.Decentralized robust output feedback control for control affine nonlinear interconnected systems ［J］.Journal of Process Control，2009，19(3):865-878.

［7］Trottemant E J，Scherer C W，Weiss M，et al.Robust missile feedback control strategies［J］.Journal of Guidance，Control，and Dynamics，2010，33(6):1837-1846.

［8］韩京清.自抗扰控制技术［M］.北京:国防工业出版社，2008:183-197.

［9］Gao Z Q，Huang Y，Han J Q.An alternative paradigm for control system design［C］//Proceedings of IEEE Conference on Control and Decision.Orlando，2001:4578-4585.

［10］钱杏芳.导弹飞行力学［M］.北京:北京理工大学出版社，2008:248-255.

［11］胡寿松.自动控制原理［M］.北京:科学出版社，2005:489-491.

［12］Nesline F W，Wells B H，Zarchan，P.Combined optimal classical approach to robust missile autopilot design［J］.Journal of Guidance，Control and Dynamics，1981，4(3):316-322.

［13］Zaks S H，Brehove J D，Corless，M J.Control of uncertain systems with unmolded actuator and sensor dynamics and incomplete state information ［J］.IEEE Transcations on Systems.Man and Cybernetics，1989，19(2):241-257.