航天器远程最优拦截方法研究①

符 俊，蔡 洪，张士峰，丁洪波

(国防科技大学航天与材料工程学院，长沙 410073)

0 引言

迄今有很多学者对空间拦截问题进行了研究，一般来说，它们可分为2类:脉冲推力，如Herrick方法、Godal方法、Gauss方法、普适变量法和 Lambert方法等［1］;有限推力，如文献［2－4］。对于有限推力拦截情况，往往是在一定的性能指标下寻找最优的拦截轨道，这是一个最优控制问题。

随着计算机水平的高速发展，求解最优控制问题的数值方法得到了广泛应用，其中鲁棒性和通用性更好的直接法往往能更好地求解动态优化问题。它将函数空间中的最优控制问题转化为欧式空间中的非线性规划问题，然后再利用各种非线性算法完成问题的求解［5］。

本文基于非线性化C-W方程，利用Legendre伪谱法(Legendre Pseudospectral Method，LPM)对航天器远程拦截轨道进行优化，同时基于固定时间飞行定理讨论了一种脉冲推力假设下的优化方案，并将这2种方法进行了对比分析。

1 数学模型

1.1 动力学方程

C-W方程常用于描述圆参考轨道下的航天器近距离相对运动，这主要是因为C-W方程在建立的过程中作了以下2个假设:(1)目标航天器的轨道为圆轨道;(2)拦截器与目标航天器之间的距离远小于它们的地心距。但在拦截问题中，假设(2)极大地限制了C-W方程的应用，因为拦截器和目标航天器之间的距离往往很大，故假设2不再成立。在这种情况下，下面给出适于描述远程拦截问题的航天器相对运动方程(目标航天器不机动):

式中 ［x y z vxvyvz］T表示拦截器在目标航天器LVLH(Local Vertical，Local Horizontal)坐标系中的相对运动状态矢量;Tx、Ty、Tz为拦截器的推力在LVLH坐标系三轴上的分量;m为拦截器的质量;Isp为拦截器推进剂比冲;a为目标航天器的地心距;g为重力加速度;μ为地球引力常数;rc为拦截器的地心距，为目标航天器的平均轨道角速度为拦截器推力

在优化问题中，控制量为 U=［Tx，Ty，Tz］T，性能指标应为拦截器消耗的燃料最少，即终端时刻质量最大:

式中 tf表示终端时刻。

1.2 无量纲化参数

采用数值方法进行优化时，必须对物理量进行无量纲化，选取的无量纲化参数如下:

式中 Rs为目标航天器的地心距;m0为拦截器的初始质量。

2 有限推力最优拦截

2.1 Legendre伪谱法简介

Legendre伪谱法由美国海军研究院Fahroo Fariba和Ross I Micheal提出［6］，它属于直接法中的一种。该方法将状态变量和控制变量在一系列LGL(Legendre-Gauss-Lobatto)点上离散，并以离散点为节点构造Lagrange插值多项式来逼近状态变量和控制变量，从而将动态最优控制问题转化为静态参数优化问题(NLP问题)。Legendre伪谱法通过对全局插值多项式求导来近似状态变量对时间的导数，从而将微分方程约束转换为一组代数约束，这些约束条件加上问题本身的约束条件，如边界约束、路径约束等，共同构成NLP问题的约束条件。Legendre伪谱法的求解步骤可参考文献［3 －4，7］。

2.2 优化结果及分析

以一具体的轨道拦截任务为例，研究Legendre伪谱法的应用。仿真条件:拦截器总质量5 00 kg，推进剂质量4 00 kg，比冲300 s，最大推力2 000 N。初始时刻 t0，拦截器的轨道根数:a=16 678.137 km，e=0.2，i=28.5°，ω =0，Ω =0，ƒ=1.54°。目标航天器的轨道根数:a=6 878.137 km，e=0，i=30°，Ω =0，u=2.05°。

经过计算，可得到t0时刻拦截器在目标航天器LVLH坐标系中的相对运动状态:

其中，前3项表示相对位置，后3项表示相对速度，距离单位为km，速度单位为km/s。

仿真计算中采用60个LGL点，优化结果见图1～图4。

图1 控制变量的优化结果Fig.1 Optimal results of control variables

图1(a)为推力随时间的变化曲线，可看出在拦截过程中，拦截器受到的推力主要沿着迹向，在另外2个方向上的分量很小。发动机工作时产生的推力一般沿体系x方向，为了使推力在LVLH坐标系三轴上的分量大小满足要求，可通过控制拦截器的姿态来实现。在本次仿真中，推力作用的时间为506.9 s，最大值为2 000 N，符合最大推力约束条件。之后的过程发动机停止工作，拦截器在地心引力的作用下飞向目标航天器进行拦截。图1(b)为拦截器的过载变化曲线图，从图1(b)可看出，最大过载出现在y方向，但均不超过1，满足容许过载较小的航天器的变轨要求。

颜晓晨正在试衣服，一个二十五六岁的长发女子走了进来，看了她几眼，拿了一套颜晓晨试穿的衣服，翻看价格牌。一个营业员在接电话，另一个营业员正低着头帮颜晓晨整理裤脚，都没顾上招呼她，颜晓晨笑着说：“全场五折。”

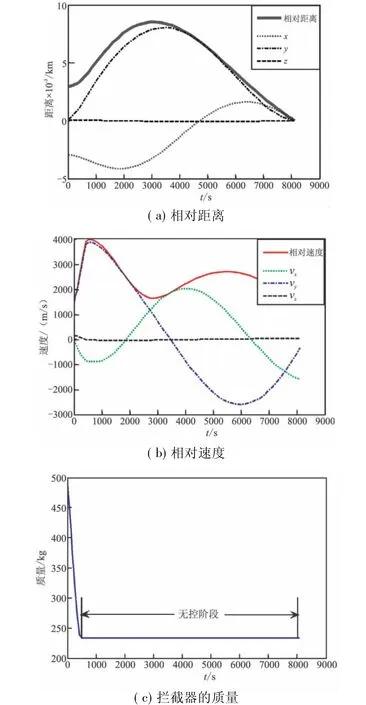
图2 状态变量优化结果Fig.2 Optimal results of state variables

图2为拦截器的状态变量优化结果图。其中图2(a)为相对距离变化曲线，可看到，经历8 080.5 s后，拦截器与目标航天器的相对距离趋于0，成功实现拦截。分析图2(a)可发现，拦截器与目标航天器的相对距离经历了一个先增大后减小的过程，而不是单调减小，这是因为性能指标为能量最省，在前面给定的初始相对运动状态条件下，如果直接控制拦截器朝目标航天器飞去，势必会消耗很大的能量，故拦截器与目标航天器之间的距离不是单调减小。图2(b)为相对速度变化曲线，图2(c)为拦截器的质量变化图。拦截器最终质量为 233.5 kg，燃料消耗为 266.5 kg。

图3 相对运动轨迹Fig.3 Trajectories of relative motion

图4 哈密顿函数随时间的变化曲线Fig.4 Time histories of Hamiltonian

图3为拦截器相对目标航天器的运动轨迹，从图3看到，它们之间的相对运动主要发生在x-y平面，是由于初始时刻两者的轨道面空间位置差异不大造成的。

在应用Legendre伪谱法处理最优控制问题时，往往面临着一个问题:解的最优性能否得到保证?这可通过求解哈密顿函数的值是否满足一阶最优性条件来进行判断:作为区别于一般直接数值解法的重要特性之一，Legendre伪谱法将最优控制问题转化为LGL点上的非线性规划问题后，可将对该问题的求解转化为对一个增广性能指标的优化求解，并能在求解该问题的同时得到Lagrange乘子，即LGL点上的协态变量值，从而计算哈密顿函数值以检验是否满足一阶最优性必要条件。如果满足则可认为结果最优，否则就不是最优的［8－9］。

本次仿真中的性能指标为J=－m(tf)，这是一个末值型的性能指标，且终端时刻自由。根据庞特李亚金极大值原理，在优化过程中，哈密顿函数值应恒为0。图4为哈密顿函数随时间的变化曲线，从图4可看到，该值一直处于0附近，最大相差为0.7%，满足最优性必要条件，因此解的最优性能够得到保证。

3 基于脉冲推力的最优拦截方案

前面利用Legendre伪谱法得到了最优拦截问题的解。下面讨论在脉冲推力假设下航天器远程最优拦截方案的研究方法，理论基础是固定时间拦截定理。

3.1 Battin-Vaughn 方法

求解固定时间拦截问题的经典算法是高斯方法和Lambert飞行时间定理。通过对上述2种算法的改进，派生出了很多算法，如海里克方法、歌德方法、普适变量法、p迭代法和Battin-Vaughan方法。其中，普适变量法算法简单，具有普适性，适用于所有的圆锥曲线，但在某些情况下，收敛速度太慢;p迭代法用牛顿迭代法来修正p的试探值，收敛速度很快，其不足在于r1、r2共线情况下不收敛;而Battin-Vaughan方法通过引入超几何函数和连分数进行数值迭代求解，迭代速度与精度均比较理想，适合计算机快速求解对于任意情况都收敛很快，具有几乎一致收敛的性质。据Klumpp在1986年以来对Battin-Vaughan算法就所有合理情况所做的广泛实验研究表明，Battin的算法对于载人和不载人自主制导都能提供所需要的可靠性、快速性和列紧性，并且对于行星轨道确定以及整个天体力学也都提供了所需要的精度和应用范围［10］。

3.2 优化方案

在空间拦截任务中，关键技术是在一个时间窗口(也称任务窗口)［t0，t1］中拦截器能命中目标并使消耗的能量最小。根据固定时间拦截定理，单圈Lambert问题存在唯一解。因此，拦截器不同的机动时刻tman对应着拦截目标航天器所需的不同速度冲量Δv，这称为一种拦截方案，以(tman，Δv)表征。根据这种思路，在实际计算过程中，首先计算出一次拦截任务中任务窗口内的所有机动拦截方案，然后在这些方案中选择一种最优的方案(比如所需特征速度最小或拦截时间最短)或者是满足特定拦截任务要求(在指定时刻拦截目标)的方案，这种灵活性是该方法的一大优点。

寻求最优拦截方案的关键是求解机动时刻tman，可采用遗传算法进行求解，也可采用枚举法，这里选择枚举法。采用枚举法寻找最优拦截方案，具体要求是在时间窗口内，选择机动时刻tman作为迭代变量，求解特征速度最小的机动方案，迭代步长可视具体情况灵活控制。为克服枚举法计算量大的缺点，可通过变步长控制计算量。求解流程见图5。

图5 仿真流程Fig.5 Flow of simulation

3.3 仿真分析

仿真条件与2.2节相同，为与伪谱法的优化结果进行对比，选择拦截器的任务时间窗口为［t0，t1］，其中t1=8 080.5 s。

图6为机动时刻与所需速度冲量的关系，横坐标表示机动时刻tman，纵坐标表示所需的速度增量Δv。t0为零时刻，可看出，当机动时刻tman=4 328 s时，所需的速度增量最小，为1 501.73m/s。

图6 机动时刻与速度冲量的关系Fig.6 Relationship of maneuver time and velocity impulse

拦截器最优变轨过程如表1所示，变轨所需的速度冲量为［1 091.58，－930.36，－445.03］(J2000 坐标系)，单位为 m/s;变轨点的轨道位置为 ƒ=241.91°，拦截点的轨道位置为ƒ=86.25°。拦截器在原轨道上运行4 328 s后开始变轨。可以看出，变轨前后拦截器的轨道面并没有改变，只是轨道的形状和大小发生了变化，因此所需的速度增量不是很大。根据公式Δv=Ispg ln(m+/m－)计算得到消耗的燃料为199.99 kg。

表1 拦截器变轨前后轨道根数Table 1 Orbital elements of interceptor

4 2种方法的比较

为便于描述，Legendre伪谱法用方法Ⅰ表示，基于脉冲推力的优化方法用方法Ⅱ表示。根据前面的分析，发现方法Ⅱ的燃料消耗要小于方法Ⅰ，其中一个原因为方法Ⅱ通过选择拦截器与目标航天器相对相位关系最优时进行变轨，如图7所示。方法I是直接在初始相对相位关系下实施拦截机动变轨，因此使得拦截消耗的能量较大。2种方法的综合对比详情见表2。

图7 拦截器变轨图Fig.7 Orbit change of interceptor

表2 2种方法的比较Table 2 Comparison of two kinds of methods

5 结论

(1)仿真过程中发现，Legendre伪谱法精度高，对变量初值不敏感，收敛半径大，适于处理航天器远程拦截问题。

(2)在有限推力拦截中，Legendre伪谱法用来优化推力的大小和方向，从而得到最优拦截轨道;而在脉冲推力最优拦截方法中，主要是通过调整拦截器和目标航天器的相位关系来搜索最优拦截轨道。

(3)与Legendre伪谱法相比，采用基于脉冲的最优机动拦截方案具有更大的灵活性，既能够满足性能指标要求，也能满足具体拦截任务要求。

［1］任萱.人造地球卫星轨道力学［M］.长沙:国防科技大学出版社.1988:141-157.

［2］涂良辉，袁建平，罗建军.基于伪光谱方法的有限推力轨道转移优化设计［J］.宇航学报，2009，29(4):1189-1193.

［3］胡正东，丁洪波，曹渊，等.伪谱法在SGKW轨道快速优化中的应用［J］.航天控制，2009，27(4):3-7.

［4］宣颖，张为华，张育林.基于Legendre伪谱法的固体运载火箭轨迹优化研究［J］.固体火箭技术，2008，31(5):425-429.

［5］罗亚中，唐国金，田蕾.基于模拟退火算法的最优控制问题全局优化［J］.南京理工大学学报，2005，29(2):144-148.

［6］Fahroo F，Ross I M.Costate estimation by a legendre pseudospectral method［J］.Journal of Guidance，Control and Dynamics，2002，24(2):270-277.

［7］Huntington Geoffrey Todd.Advancement and analysis of a gauss pseudospectral transcription for optimal control problems［D］.Cambridge，Massachusetts Institute of Technology，2007:115-143.

［8］Qi G，Ross I M，Wei K，et al.Connections between the convector mapping theorem and convergence of pseudospectral methods for optimal control［J］.Compute Optimal Application，DOI.10.1007/s10589-007-910-2-4，2007(1):1-29.

［9］丁洪波，蔡洪，张士峰，等.高超声速滑翔式再入飞行器最大航程飞行轨迹分析［J］.国防科技大学学报，2009，31(6):67-72.

［10］赵瑞安.空间武器轨道设计［M］.北京:中国宇航出版社，2008:176-178.

［11］Richard H Battin.An introduction to the mathematics and methods of astrodynamics［M］.AIAA Education Series，AIAA，Reston，VA，1999.