基于改进协同优化方法的固体运载火箭多学科设计优化①

杨希祥，张为华

(国防科学技术大学航天与材料工程学院，长沙 410073)

0 引言

固体运载火箭设计是极其复杂的理论和工程问题，涉及气动、推进、弹道、质量等多个学科，各学科相互耦合和影响。传统设计方法在方案设计阶段往往对设计知识应用不充分，学科分配不合理，采用串行模式，割裂各学科间耦合关系，不能有效集成各学科知识进行设计，导致运载火箭设计水平低、周期长、成本高、风险大。多学科设计优化(Multidisciplinary Design Optimization，MDO)是解决上述问题的有效方法。MDO是当今飞行器设计领域最活跃的研究方向之一［1］。

MDO核心是分解协调算法，分为单级优化算法和多级优化算法。多级优化算法中的协同优化方法(Collaborative Optimization，CO)以结构简单、分解协调机制与现有飞行器设计专业划分和协调关系一致等显著特点在飞行器MDO领域得到广泛应用。文献［2］研究了CO在单级入轨运载器设计优化中的应用，并同传统串行设计方式及AAO方式进行了对比，结果表明CO存在明显优势;Perez等采用自适应罚函数法将系统级优化转换为无约束优化问题，改进了CO，并将其应用于飞机飞行动力学与控制MDO［3］;文献［4］采用增强CO求解助推-滑翔导弹设计问题，设计结果表明，CO适用于助推-滑翔导弹多学科设计优化。

本文研究CO在新型多级固体运载火箭设计优化中的应用。研究的运载火箭采用三级固体发动机+液体末助推串联式结构布局，运载火箭一级飞行段姿态控制采用栅格舵。

1 固体运载火箭多学科分析模型

1.1 总体学科分析模型

总体学科分析模型任务是，在给定固体运载火箭级数、运载能力要求前提下，设定飞行过程速度损失量(重力和阻力引起)、各子级发动机比冲、各子级结构质量系数和各子级提供的需要速度增量，计算各子级质量及起飞质量。

设末助推级干重和卫星质量总和为M，目标轨道高度h，飞行过程总速度损失为Δv1，各级固体发动机比冲分别为 Isp1、Isp2、Isp3，子级结构质量系数分别为σ1、σ2、σ3，三级固体发动机与液体末助推级提供的速度增量与实际需要的入轨速度增量比分别为α、β、γ、1－α－β－γ，液体末助推级发动机比冲为Isp4。

卫星进入目标轨道需要的速度增量:

式中 R为地球半径;μ为引力常数。

末助推级消耗液体燃料质量:

各级提供速度增量分别为 αΔv、βΔv、γΔv、(1 － α－β－γ)Δv，自顶向下求取各级质量:

式中 mpi(i=1，2，3)为第i子级发动机药柱质量;msi(i=1，2，3)为第i子级结构质量;m0为全箭初始起飞质量。

1.2 推进学科分析模型

推进学科分析模型的任务是，根据给定的各级发动机药柱和结构参数，进行热力计算、性能损失计算、药柱设计计算、内弹道计算、质量计算，最终得到推力-时间曲线T(t)，压强-时间曲线p(t)和质量-时间曲线m(t)。

根据给定的推进剂配方、初温、燃烧室压强和环境压强，采用最小自由能法进行发动机热力计算，得到理论比冲，利用经验公式进行两相流损失、扩散损失、边界层损失、燃烧损失、喷管潜入损失、化学动力学损失和喷喉烧蚀损失等性能损失计算，得到发动机实际比冲［5］。

翼柱形三维药柱计算采用通用坐标法。翼柱形药柱外边界构造采用轴向圆柱、椭球表面加上轴向圆环带组合而成，药柱内腔由轴向圆柱、圆锥台和轴向圆环带组成。翼片构造较复杂，为适应优化设计需要，减少优化计算量，采用等宽度翼片。常规通用坐标法计算药柱燃烧面积等参数时，药柱几何构型和几何尺寸必须完全确定，而在发动机优化设计中，药柱几何构型和几何参数通常不确定，有些参数本身就是设计变量。因此，本文对常规形式通用坐标法进行改进以适应优化设计需要。将翼柱形药柱分为前翼、后翼和前后翼3种，翼片形状也分为若干种类型，分别编制标准程序块完成各种翼柱形药柱前处理，调用通用坐标法进行燃面计算［6］。

固体发动机一维内弹道计算相对零维方法精度较高，但由于采用三重迭代计算方法，计算时间较长，嵌入优化过程进行内弹道计算将严重降低优化效率;零维方法计算速度较快，且经过适当修正，能够满足总体设计阶段计算精度要求。因此，本文采用零维内弹道计算模型。由内弹道计算得到发动机燃烧室压强-时间曲线，进而得到发动机推力-时间曲线。

发动机质量包括药柱质量、燃烧室壳体质量、绝热层和包覆层质量、前后接头质量、喷管质量、点火器质量等。药柱质量由通用坐标法计算得到的药柱体积乘以药柱密度得到;按展开型质量模型计算燃烧室壳体、绝热层、包覆层、前后接头、喷管等部件结构质量。点火器、安全点火机构、前顶盖及发动机紧固件等质量看做固定质量，参照相关工程型号设计［7］。

1.3 气动学科分析模型

气动学科分析模型的任务是，根据给定的运载火箭箭体、箭翼和整流罩初始输入外形参数及发动机设计结果生成的外形参数，计算阻力系数Cd(Ma，α)和升力系数 C1(Ma，α)。

本文在进行固体运载火箭设计优化时，主要考虑发动机设计结果引起的气动外形参数变化和整流罩外形变化，栅格翼外形参数保持不变。气动力系数计算采用如下方法，首先不考虑栅格翼，采用基于DATACOM开发的气动特性估算程序计算常规气动布局的运载火箭气动力系数，得到关于攻角α和飞行马赫数Ma的阻力和升力系数矩阵，然后采用修正系数对得到的阻力系数和升力系数进行修正，得到最终的气动力系数。

修正系数χCd和χC1基于CFD计算获取，它们在全程飞行中是时变的。影响修正系数的因素很多，为研究问题方便，本文基于文献［8］研究结果，主要考虑一子级发动机直径、全箭长度、α和Ma对修正系数影响。以χCd为例，将它看做上述4个变量的函数，采用拉丁超立方设计方法在变量空间选取一定数目训练样本点，通过CFD计算获取对应条件的χCd值，采用二阶多项式拟合出χCd与4个变量的函数关系:

式中 x［d1，L，α，Ma］、a0、ai和 aij为多项式系数。

1.4 质量学科分析模型

质量学科分析模型的任务是，分析计算除发动机质量和有效载荷质量以外的其余质量，包括尾段质量、各级间段质量、整流罩质量、尾段和级间段内单机和仪器设备质量、仪器/推进舱质量等。为研究问题方便，尾段质量、各级间段质量、整流罩质量采用导出型质量方程进行计算，即根据已有成熟型号中各部分质量间的联系形式和相对质量系数获取。尾段和级间段内单机和仪器设备质量根据已有成熟型号确定且保持不变。仪器舱内控制系统(姿态敏感器、惯导、计算机等)、遥外测系统等电气系统质量在优化过程中保持不变，姿轨控动力系统中高压气瓶、管路和其余零部件质量取为定值，只考虑液体推进剂质量变化引起的储箱质量变化。

仪器/推进舱内液体燃料采用球形共体储箱，即双组元推进剂共用一个球形壳体，中间靠2层金属波纹隔膜实现推进剂有效隔离。在已知储箱材料的前提下，根据“同一储箱厚度处处相等且保持不变”原则计算储箱质量。

1.5 弹道学科分析模型

弹道学科分析模型的任务是，根据其余各分系统设计结果和设定的飞行程序，完成星箭一体化飞行器自发射至入轨的全过程飞行仿真，根据仿真结果对助推系统性能进行评估，并计算重力和阻力造成的速度损失 Δv1。

弹道学科采用发射坐标系下三自由度弹道仿真模型，飞行程序设计详见文献［9］。

2 多学科协同优化设计框架

给定运载能力要求和目标轨道，固体运载火箭多学科设计优化的目标函数选为起飞质量m0最小，各学科相关的设计变量包括:

(1)总体学科:一、二、三子级提供的速度增量与需要的总速度增量比值α、β、γ;

(2)动力学科:各级发动机外径di(取整，且根据我国已有发动机型号直径就近取值)，燃烧室工作压强pci，喷管膨胀比εi，燃烧室圆筒段长度 Lci，翼柱形药柱翼长 lei、翼顶长 ldi、翼深 hei、翼宽 wei，药柱通道直径 dpi(i=1，2，3);末助推液体推进剂质量mp4;

(3)气动学科:整流罩外形控制参数，外形表示采用非均匀有理B样条曲线，控制点选取参见文献［10］;

(4)弹道学科:包括初始发射方位角A0，飞行程序角控制参数三级滑行时间 t3h。

固体运载火箭多学科分析流程如图1所示。

图1 固体运载火箭多学科分析Fig.1 Multidisciplinary analysis of solid launch vehicle

分析图1上图中学科耦合关系，如果将总体、推进、质量和气动学科综合为运载火箭子模块，弹道学科保持不变，则图1上图可重新表示为下图形式。于是，可将运载火箭多学科设计优化看做运载火箭本身和弹道学科2个大系统耦合的两学科设计优化问题。这种流程转化关系，一方面可得到更为清晰、明确的协同优化设计框架，更重要的是，采用转化后的两学科设计框架，可大大减轻采用5个学科同时并行设计带来的下文协同优化框架系统级设计变量规模过大问题。

设计优化的约束条件包括:

(1)长细比约束:L/d1≤C，L为全箭长度，C为常数;

(2)上面级直径不小于下面级直径:d1≤d2≤d3;

(3)终端入轨条件约束:|h(tf)－H*|≤ε1，|v(tf)－ v*|≤ε2，|i－ i*|≤ε3，e≤ε4;

(4)飞行过程动压和过载约束:q≤qmax，nx≤(nx)max，ny≤(ny)max;

(5)大气层飞行段攻角约束:|α|≤αmax;

(6)一子级关机高度约束:|H1|≥hmin;

(7)起飞推重比约束:|μ0|≥μmin;

(8)各级发动机燃烧室最大压强和平均压强比约束:pmax，i/pc，i≤λmax，i，(i=1，2，3);

(9)整流罩驻点热流密度约束(一级关机点):qw≤qw，max;

3 含序贯策略的改进协同优化方法

协同优化方法(CO)将原有设计优化问题分为两级，一个系统级和多个并行的学科级，通过将学科级耦合状态变量作为系统级设计变量处理，避免了求解非线性耦合方程组问题，但对于学科间耦合变量较多问题，例如上述固体运载火箭多学科设计优化问题，这种方式会造成系统级设计变量规模过大，进而导致优化问题求解困难，甚至无法求解。同时，标准CO系统级采用一致性等式约束对学科间不一致进行协调，但等式约束严格满足只是一种理想状态，实际问题一致性等式约束很难同时满足，导致系统级进行大量迭代甚至无解。

针对上述问题，本文在保持CO基本架构前提下，对耦合过于紧密学科，引入序贯执行策略，将输出状态变量较多学科的状态变量不再作为系统级设计变量，而是直接传给需要这些状态变量的另一学科，两学科间不再采用标准CO的并行计算策略，而是采用序贯执行策略，其余学科优化计算仍采用标准CO并行运行策略。同时，为改善收敛性能，提高求解精度，上述采用序贯策略的协同优化方法，消除系统级一致性等式约束带来的求解困难，借鉴序列超球子空间思想［11］，采用动态松弛算法处理系统级等式约束，定义学科间不一致信息:

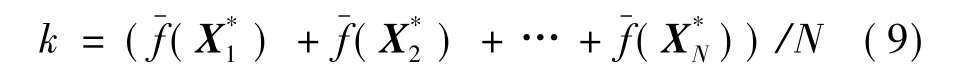
进而定义动态松弛变量 s=(λ ×k)2，(0.5≤λ≤1)系统级等式约束转化为不等式约束:

这种方式可有效克服系统级一致性等式约束带来的求解困难，保证形成的新系统级优化问题满足KKT条件，又兼顾学科间一致性要求，计算量小，程序编制简单。

基于上述改进策略的CO，固体运载火箭多学科设计优化框架如图2所示。

图2 固体运载火箭协同设计优化Fig.2 Collaborative optimization of solid launch vehicle

4 设计优化结果与分析

求解上述固体运载火箭多学科设计优化问题，系统级和运载火箭子模块优化采用在文献［9］中提出的控制参数改进型粒子群优化方法，弹道学科优化采用基于粒子群和序列二次规划方法的组合优化方法，优化算法参数设置如下:

(1)运载火箭学科优化器:粒子群规模60，惯性权重最大值 0.9，最小值 0.1，学习因子最大值 2.5、最小值0.5，函数拉伸方程中 λ1取 108，λ2设为 0.5，μ 为10－5。

(2)弹道学科优化器:粒子群规模30，惯性权重0.5，学习因子均取 1.5，交叉概率 0.5，粒子群算法优化20代后转为采用序列二次规划方法进行优化。

(3)系统级优化器:粒子群规模20，惯性权重最大值0.9，最小值0.2，学习因子最大值 2.5，最小值 0.5，函数拉伸方程中 λ1取 108，λ2设为 0.5，μ 为 10－5，ε1取为 0.5，ε2取为0.1。

约束条件设为:

(1)L/d1≤14.0;

(2)|h(tf)－ 300 000|≤3 000 m;e≤10－3;|i－96.67°|≤0.015°，|v(tf)－7 725.84|≤2 m/s;

(3)q≤0.007 5 MPa，nx≤16g，ny≤0.1g;

(4)|α|≤3.5°;

(5)|H1|≥20 000 m;

(6)|μ0|≥1.35;

(7)pmax，i/pc，i≤1.2(i=1，2，3);

(8)qw≤50 000 W/m2。

系统级经过4次迭代达到收敛，设计变量取值范围及优化结果如表1所示。

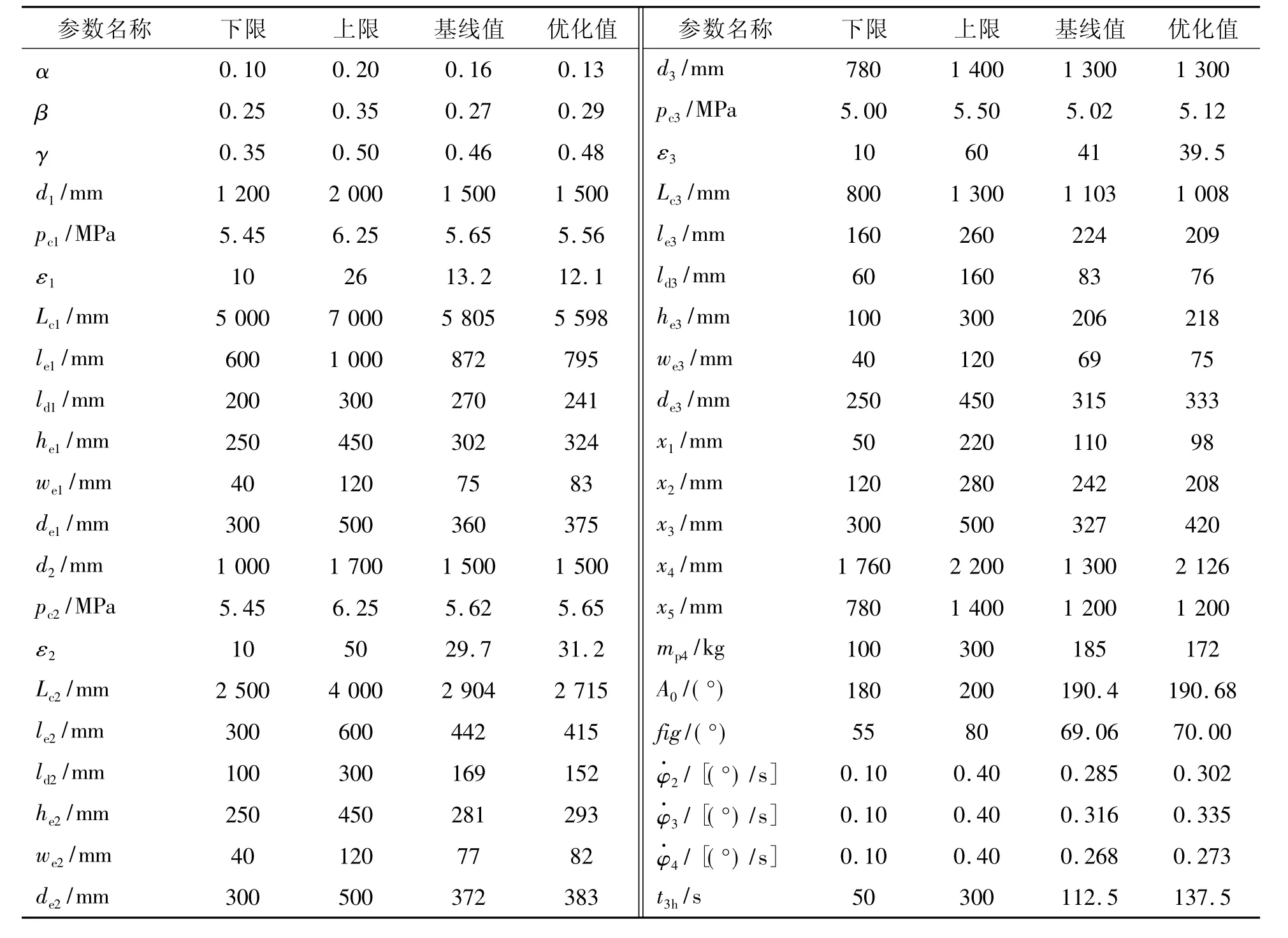
表1 设计优化结果Table 1 Optimization design results

入轨质量取定为基线方案值，优化方案起飞质量(33 498 kg)比基线方案(36 060 kg)减小7.1%，各项约束得到良好满足，表明多学科协同设计优化可有效综合挖掘各学科设计潜力，大大提高固体运载火箭设计水平。采用本文提出算法，只需在优化设计开始时，设置合理的设计变量区间，设计经验和设计知识较少时，可指定相对较大的变量区间，同时采用较大的粒子群规模，大大降低了设计难度。优化过程中，系统级每个粒子向子系统级传递的目标设计变量值，子系统级总能通过设计优化获得可行解，并将结果返回系统级，无需人为介入，表明优化算法具有较高的智能化和自动化设计水平。

优化过程系统级群体粒子分布变化过程如图3所示，图中圆圈内的解表示最优解。由图3可看出，随着迭代进行，粒子开始聚集，群体最优解值得到改进。需要注意的是，优化第2代、第3代、第4代群体最优值相同。优化方案发动机推力-时间曲线如图4所示，优化方案得到的固体发动机推力-时间曲线具有递增特性。

图3 优化过程粒子分布变化Fig.3 Change of particle swarm position during optimization process

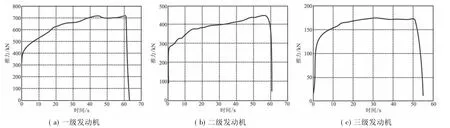
图4 优化方案发动机推力-时间曲线Fig.4 Change of thrust vs time for optimal scheme

5 结论

(1)建立了固体运载火箭多学科设计优化相关学科分析模型;构建了多学科协同设计优化框架。

(2)开展了协同优化方法(CO)改进研究。针对固体运载火箭多学科设计优化中存在的学科间强耦合问题，提出了含序贯策略改进CO，强耦合学科间采取序贯执行策略，解决了耦合变量过多带来的系统级设计变量规模过大问题，采用动态松弛策略处理系统级约束条件，消除了严格等式约束带来求解困难的问题。

(3)采用提出的含序贯策略的CO解决了固体运载火箭多学科设计优化问题，实现了固体运载火箭方案设计的智能化和自动化，提高了设计水平，降低了设计难度。

［1］王振国，陈小前，罗文彩，张为华.飞行器多学科设计优化理论与应用研究［M］.北京:国防工业出版社.2006.

［2］Braun R D，Kroo I M.Collaborative approach to launch vehicle design［J］.Journal of Spacecraft and Rockets，1997，34(4):478-486.

［3］Perez R E，Liu H H T.Multidisciplinary optimization framework for control-configuration integrated in aircraft conceptural design ［J］.Journal of Aircraft，2006，43(6):1937-1948.

［4］王健，何麟书.基于增强协同优化的助推-滑翔导弹概念研究 ［J］.宇航学报，2009，30(6):2436-2440.

［5］张为华.固体弹箭推进系统性能分析及飞行试验仿真技术研究［D］.长沙:国防科学技术大学，1999.

［6］青龙.固体火箭发动机总体优化设计［D］.长沙:国防科学技术大学，2003.

［7］《世界航天运载器大全》编委会.世界航天运载器大全(第2版)［M］.北京:中国宇航出版社，2007.

［8］吴甲生，雷娟棉.制导兵器气动布局与气动特性［M］.北京:国防工业出版社，2008.

［9］杨希祥，江振宇，张为华.基于粒子群算法的固体运载火箭上升段弹道优化设计研究［J］.宇航学报，2010，31(5):1304-1309.

［10］Jae-Woo L，Byung-Young M，Yung-Hwan Byun.Multi-point nose shape optimization of space launcher using response surface method［C］//40th AIAA Aerospace Sciences Meeting ＆ Exhibit.Reno，NV，2002:1-12.

［11］李响，李为吉.基于超球近似子空间的协同优化方法及应用研究［J］.西北工业大学学报，2003，21(4):461-464.