椭圆的“姊妹椭圆”与“姊妹圆”及其性质
●姜坤崇 (杨浦区彰武路同济新村224号甲 上海 200092)
性质1 如图1,设P是椭圆E1上的任意一点,E1在点P处的切线交椭圆E于点A,B,椭圆 E 在点 A,B 处的切线交于点 Q,记 kOA,kOB分别
为直线OA,OB(O为E的中心,以下同)的斜率,则
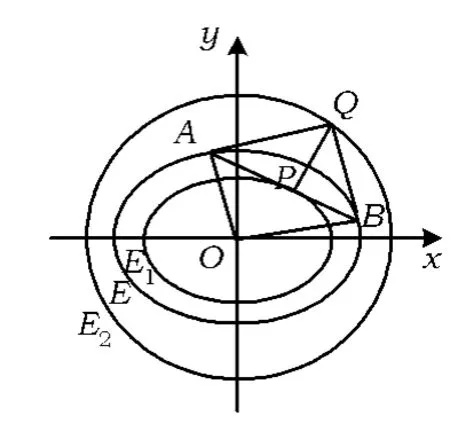
图1
(2)点 Q 在 E2上,且∠AQB=90°;
(3)AB⊥PQ.
证明设 P(x0,y0),Q(x',y'),A(x1,y1),B(x2,y2),则由点 P 在 E1上知
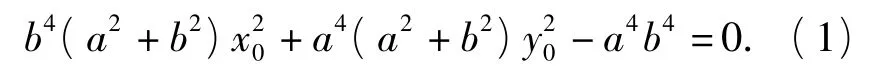
切线AB的方程为
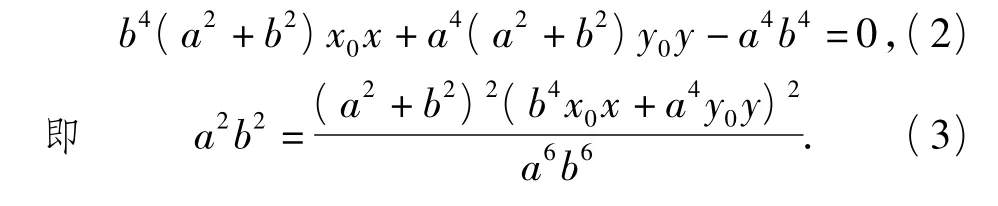
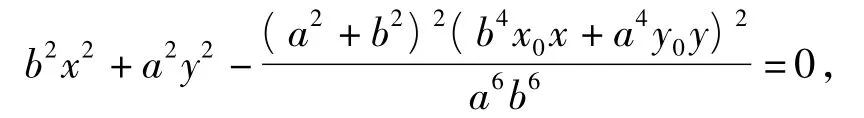
两边同除以x2,可得
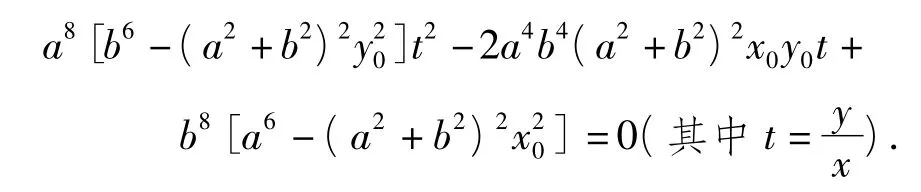
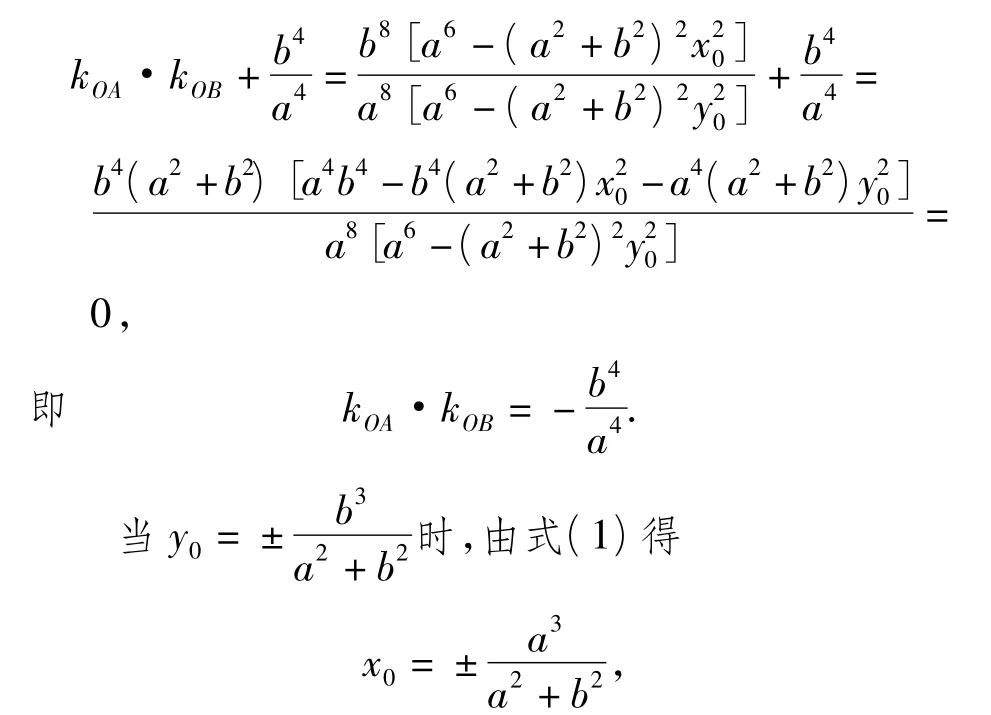
(2)由AQ,BQ分别为椭圆E过点A,B的切线知其方程分别为
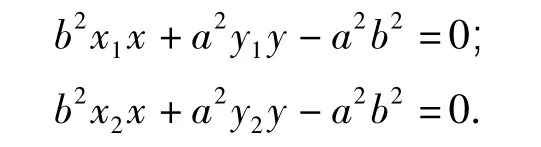
由点Q(x',y')分别在2条切线上得
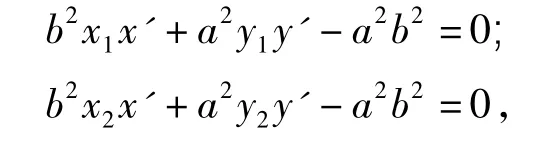
从而椭圆E的切点弦AB的方程为
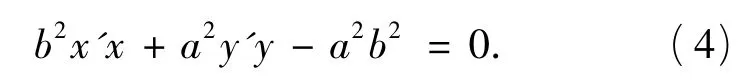
又知AB的方程为式(2),由直线重合的条件可得
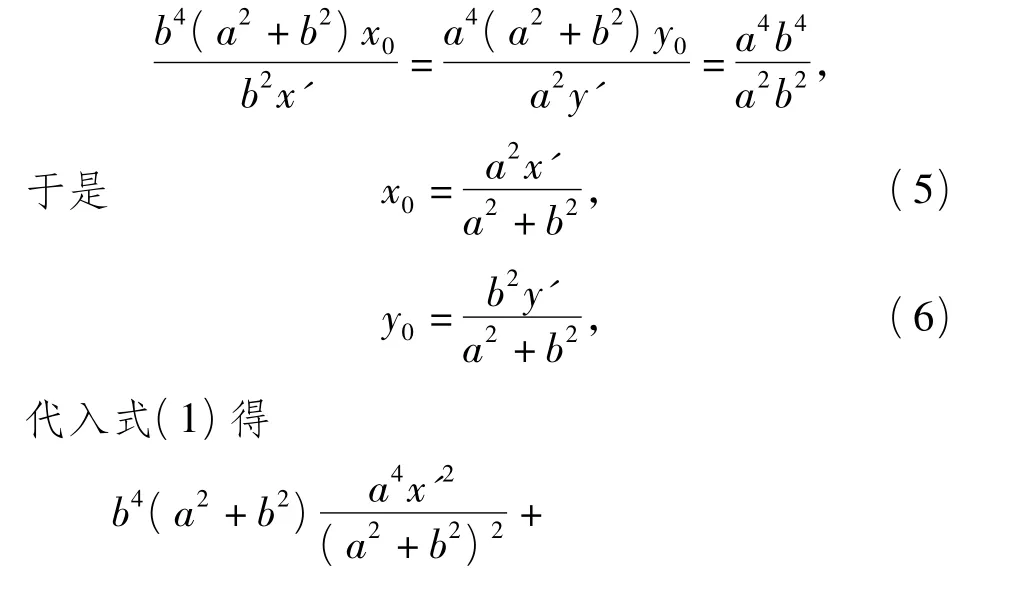
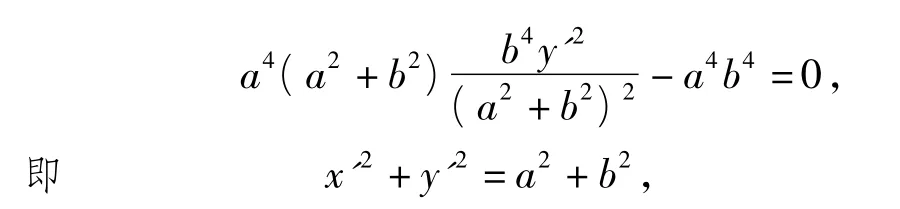
这表明点Q在E2上.以下证明∠AQB=90°.
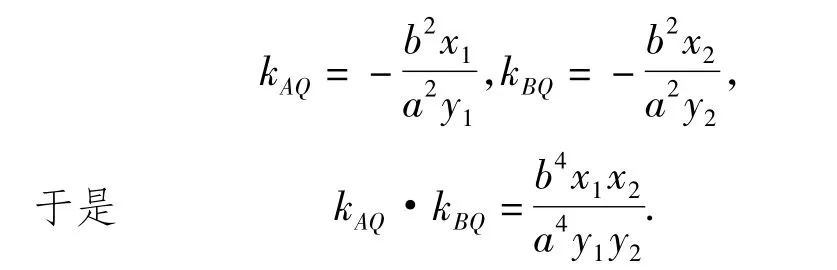
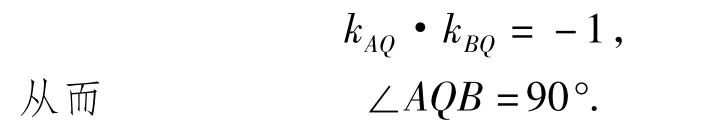
(3)当 x0y0≠0 时,由式(5),式(6)得
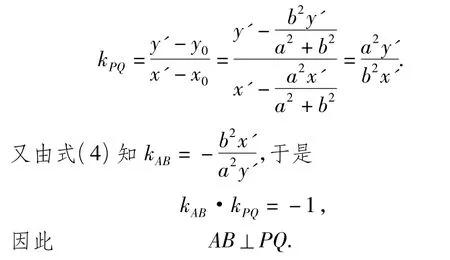
当x0y0=0时,不难证明亦有AB⊥PQ,此处从略.
性质2 如图2,设P是椭圆E上的任意一点,过点P引椭圆E1的2条切线,切点分别为 A,B,直线 PA,PB分别交椭圆E于另一点C,D.记 kPA,kPB分别为直线PA,PB 的斜率,则
(1)点 C,O,D 共线;
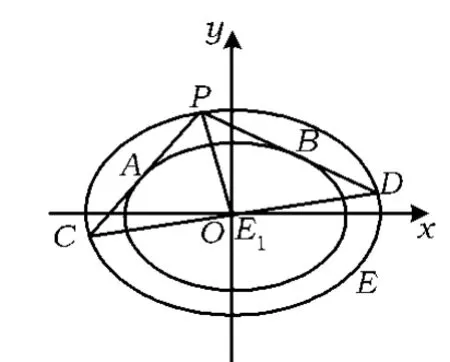
图2
证明(1)当点P不在2条坐标轴上时,直线OP的斜率存在且不为0.因为直线PC,PD分别切椭圆E1于点A,B,故由性质1的结论知
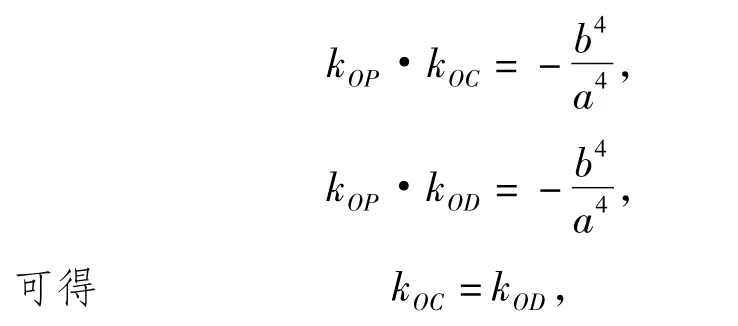
从而点C,O,D共线.
当点P在y轴上时,不妨设点P为(0,b),此时由性质1的证明过程知2条切线PA,PB的方程为±bx+ay-ab=0,从而点C,D在 x轴上,故点C,O,D 共线.
同理可证,当点P在x轴上时,亦有点C,O,D共线.
(2)设 P(x0,y0),C(x1,y1),则
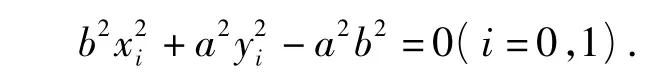
由第(1)小题的结论可知点 C,O,D共线,于是D(-x1,-y1).
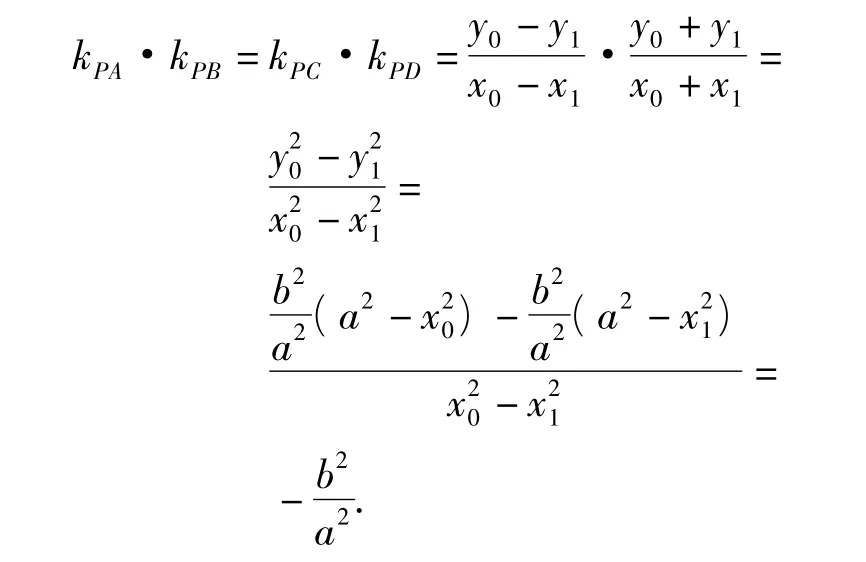
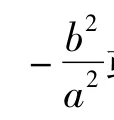
证明设 P(x0,y0),A(x1,y1),B(x2,y2),则
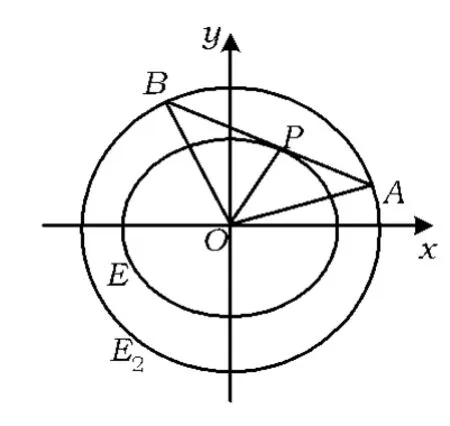
图3
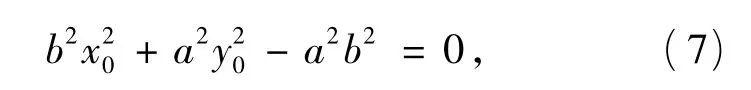
切线AB的方程为
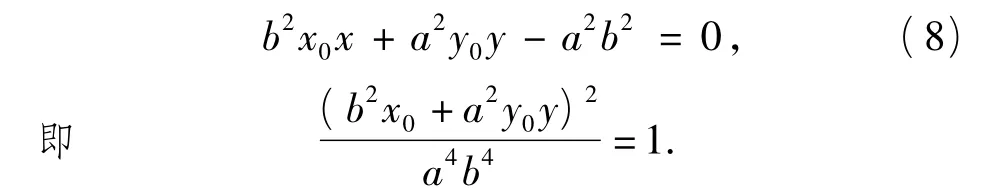
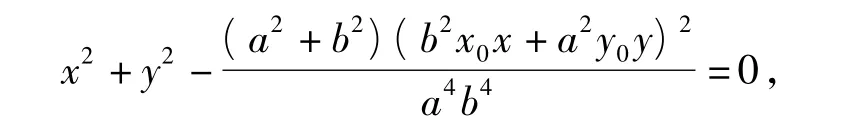
上式整理后2边同除以x2,得
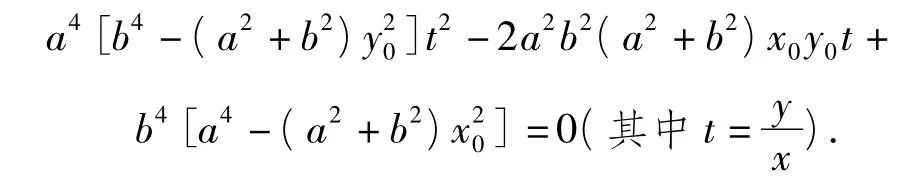

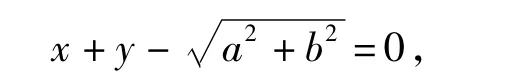
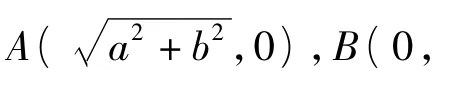
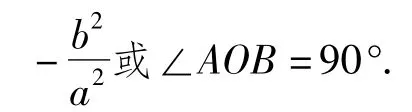
性质4 如图4,设P是圆E2上的任意一点,过点P引椭圆E的2条切线,切点分别为 A,B.记kOA,kOB分别为直线 OA,OB 的斜率,则
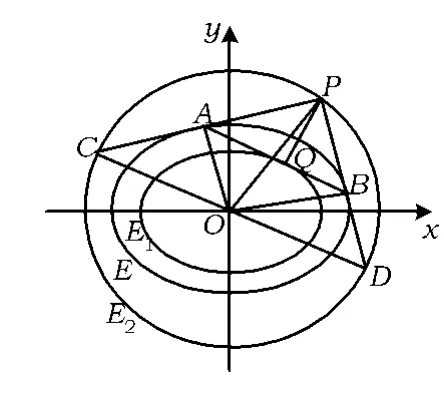
图4
(1)∠APB=90°;
(2)直线AB与椭圆E1相切,设切点为Q,有AB⊥PQ;
证明(1)当点P不在2条坐标轴上时,直线OP的斜率存在且不为0.设直线PA,PB分别交E2于点C,D,由于PC,PD分别和椭圆E相切于A,B,故由性质3的结论得
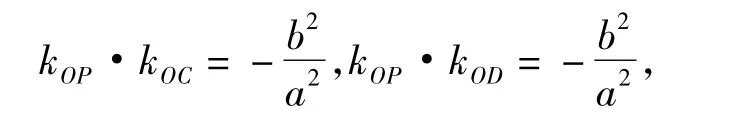
于是kOC=kOD,即 CD过中心 O,CD为圆 E2的直径,从而∠APB=∠CPD=90°.
(2)设 P(x0,y0),A(x1,y1),B(x2,y2),则
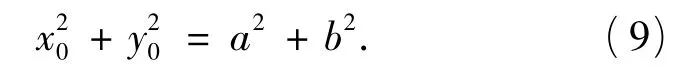
由PA,PB为椭圆E过A,B所引的2条切线知其方程分别为
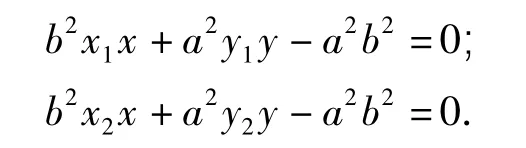
由P分别在2条切线上得
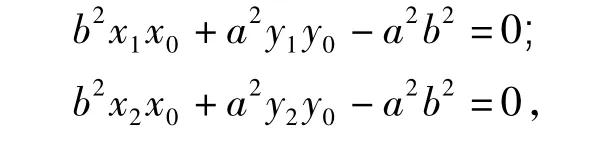
从而椭圆E的切点弦AB的方程为
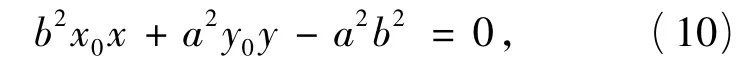
当y0≠0时,由式(10)得
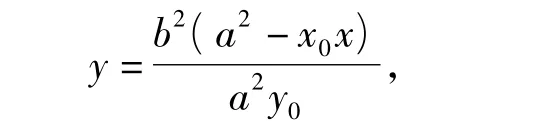
代入E1的方程整理得(用到式(9))
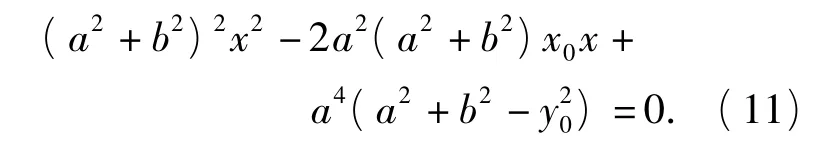
设关于x的二次方程(11)根的判别式为Δ,注意到式(9),有
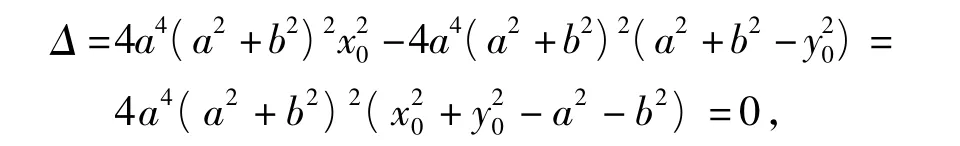
从而直线AB与椭圆E1相切.设切点为Q(x',y'),则由方程(11)、(10)及式(9)可得

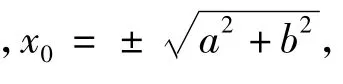
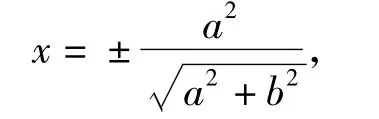
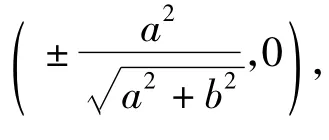
(3)当 x0≠ ±a 时,y0≠ ±b,由第(2)小题的证明过程可知
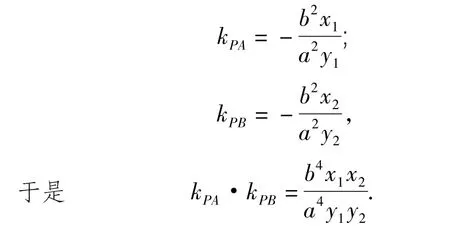
又由第(1)小题的结论知∠APB=90°,所以
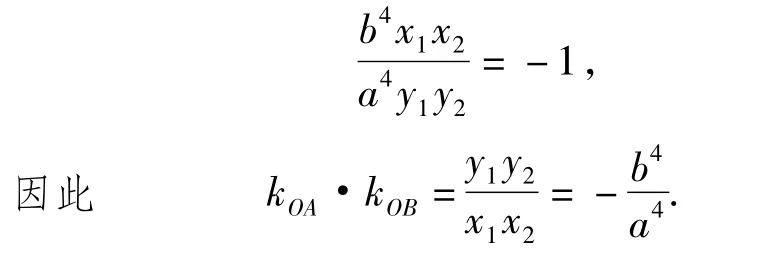
当x0=±a时,不妨设x0=a,则y0= ±b,此时过点P所引椭圆E的2条切线方程为x=a,y=b(或y=-b),2个切点在 2条坐标轴上,显然∠AOB=90°.
[1] 姜坤崇.相似椭圆的性质又探[J].数学通讯(下半月),2011(4):36-37.

